基于LM-BP神经网络的非线性轮廓图优化方法研究

许　静　何　桢　袁　荣

天津大学，天津，300072



基于LM-BP神经网络的非线性轮廓图优化方法研究

许静何桢袁荣

天津大学，天津，300072

将正交试验设计理论与BP神经网络模型和Levenberg-Marquard算法相结合，提出了一种基于LM-BP神经网络模型的针对输出为非线性轮廓图响应的离线设计优化方法。并结合实例与传统的统计回归建模方法得出的优化结果进行了比较。结果表明基于LM-BP神经网络建模可以避免由于实验误差和试验设计方案所造成的模型系数估计误差，而与标准的BP算法比较，克服了标准BP算法性能不稳定、收敛速度慢、收敛精度低、存在局部最小值等缺点，具有极高的精确性，优化结果令人满意。

BP神经网络； Levenberg-Marquard算法；试验设计；非线性轮廓图

0　引言

随着工业技术的发展，产品(过程)越来越复杂，顾客需求越来越具有多样性，加之对系统设计问题研究的深入，我们常常遇到通过某种函数关系要比通过一元变量，甚至多元变量能更充分地描述质量特性[1]。这种描述产品(或过程)质量特性的函数关系称为轮廓图(profile)[2]。在现阶段的轮廓图问题研究中，大部分是针对线性轮廓图展开的。关于非线性轮廓图问题，控制阶段的研究内容相对丰富，如William等[3]和Zou等[4]分别提出了基于参数和非参数的非线性回归模型，Jensen等[5]提出了基于T2的非线性固定轮廓，Taguchi等[6]提出了基于指数加权滑动平均(EWMA)的非参数固定效应模型分析方法，Chiken等[7]提出了基于惩罚函数的多元统计监控问题。而针对非线性轮廓图的线下优化问题研究较少。这就使得非线性轮廓图优化问题研究具有重要的现实意义。传统统计回归建模方法通过对拟合模型系数和方差的优化，实现对轮廓图的优化。由于受到实验误差和试验设计方案的影响，统计回归建模法常常会造成模型系数估计偏差，影响最终的优化效果。此外，与线性轮廓图相比，非线性轮廓图模型回归难度很大，基于回归分析的方法，需要操作者具有扎实系统的统计理论知识，可操作性困难，普适性欠缺。基于此，本文应用试验设计离线优化技术，提出了一种基于LM-BP神经网络的非线性轮廓图(non-linear profile)优化方法，并结合注射铸模机工作实例，对所提方法进行验证，结果令人满意。

1　理论介绍

1.1试验设计理论

试验设计方法包括以Box等[8]为代表的西方统计质量专家提出的经典试验设计方法和以日本著名管理实践专家田口玄一博士开发的田口试验设计方法[9]。经典试验设计主要包括因子试验和响应曲面法(response surface method，RSM)，因子试验又分为全因子试验和部分因子试验。田口试验设计方法是一套全新的试验设计方法，被称为内外表法，其目的是通过试验设计寻找可控因子的最佳因子水平，使得系统响应对噪声因子的波动不敏感。田口方法不仅可应用于生产制造阶段，而且更主要应用于工艺设计、产品设计和技术开发阶段，其将质量问题的解决思路前推至产品的开发设计阶段。

1.2三层BP神经网络拓扑原理

BP神经网络为前馈神经网络，由McCleland等[10]于20世纪80年代中期提出，它是按照前馈错误反向传播算法训练单向传播多层前向网络。本文采用隐含层数为1的三层神经网络，拓扑结构如图1所示。其中，n为输入层节点数，输入向量为Xk；输出层节点数为m，实际输出向量为Yk=(y1，y2，…，ym)，隐含层节点数为h，whi为输入层与隐含层各个节点的连接权重集合，wjh为隐含层与输出层各个节点的连接权重集合，标准的BP算法是基于纠错原则的梯度下降法(gradient proaches)。通过网络输出误差的反向传播，对各个输入层和输出层的连接权重进行调整和修改，使误差函数平方和达到最小，由于优化的目标函数结构复杂，导致收敛曲线呈锯齿状，当神经元输出接近0或1时，收敛曲线进入平坦区，网络停止训练，同时BP算法在训练神经网络时，需要预先设定步长的更新规则，这会导致算法低效。

图1　三层BP神经网络拓扑图

2　 LM-BP神经网络

鉴于BP算法的缺陷，本文利用LM(Levenberg-Marquard)算法对BP神经网络进行优化训练，建立基于LM算法的BP神经网络模型。LM算法又称阻尼最小二乘法。它是通过阻尼因子来实现与较高的迭代收敛速度的自适应调整的，它集中了梯度下降法和Gauss-Newton法两种算法的优点，在许多非线性优化问题上有着广泛的应用[11]。不同于标准BP算法误差沿着单一负梯度方向迭代，Levenberg-Marquard优化算法允许迭代误差沿着恶化的方向进行搜索，通过阻尼因子在Gauss-Newton法和梯度下降法之间自适应调整来实现网络权值的优化，使网络能够有效地收敛，大大提高了网络的收敛速度和泛化能力。LM算法在一定程度上克服了标准BP神经网络收敛速度慢、很容易陷入局部极小的缺陷。

2.1LM-BP优化算法介绍

假设Sl表示第l(l=1，2，…，L)次迭代的权值和阈值所组成的向量，Sl+1为新的权值和阈值组成的向量对于一个三层的神经网络，其LM-BP算法为

(1)

或者为

(2)

(3)

其中，J(Sl)为误差对权值偏导的雅可比矩阵；I为单位矩阵；E(Sl)为误差向量；μ为阻尼因子，为大于0的常数，当μ=0，LM-BM算法即为Gauss-Newton算法，当μ取很大值时，LM-BP算法则接近于梯度下降法。

2.2LM-BP算法的步骤

在LM算法中，阻尼因子μ通过一个进步因子φ(0<φ<10)进行自适应调整。算法开始，μ取某一较小正值，若某次迭代误差函数值E(S)不能减小，则令μ乘以φ，增大阻尼因子重复前次迭代；若某次迭代误差函数值E(S)减小，则令μ除以φ，减小阻尼因子，继续运算。算法的执行步骤如下：

(1) 设置参数，确定目标误差ε、初始阻尼因子μ0、进步因子φ。

(2)计算网络的输出y(x)，利用式(3)计算目标误差平方和El。

(3)计算矩阵J，并按照式(1)修正权值：

(4)若El<ε(ε为一极小值)，则转到步骤(2)，否则，则以Sl+1为权值计算误差El+1。

(6)当梯度的模小于给定值，或平方误差和小于某个目标误差时，算法被认为收敛，停止。

3　DOE理论和LM-BP神经网络模型相结合的非线性轮廓图优化方法介绍

三层BP神经网络可以以一定精度拟合任意函数。首先根据研究问题，设计正交试验，收集样本数据。其次，根据实验具体要求，确定神经网络拓扑结构，设置网络参数初始值。然后选择合适的优化算法对已建立的神经网络进行优化训练，反复调整权值使误差精度符合预设要求。当误差精度达到预设要求时，神经网络训练结束，输入与输出之间的函数关系也已建立。最后通过训练好的神经网模型，对可控因子进行调整，使其达到最优水平。具体步骤如下：

(1)利用正交试验理论确定关键变量，安排实验，收集样本数据。

(2)根据收集的数据情况及实验目的，确定LM-BP神经网络的模型结构，并用LM算法对所建立的BP神经网络进行优化。网络训练过程如下：

①准备训练样本，对响应数据归一化处理。不同量纲的数据直接输入网络会严重影响网络的收敛速度，因此需要对输入数据进行预处理。数据预处理选择最值归一法。公式如下：

(4)

②确定网络结构。隐含层采用如下经验公式获得：

(5)

其中，h为隐含层节点数，n为输入层节点数，m为输出层节点数，a为1～10之间的常数。

③设定传递函数。BP神经网络的传递函数常见的有Log-sigmoid型对数函数、Tan-sigmod型正切函数和purelin型线性函数。Logsig型输出值为[0,1]；tansig型输出值为[-1,1]；Purelin型输出值可取任意值。本文输出为2水平可控因子，其值为[-1,1]，所以本文选取Tansig作为网络的传递函数。

④设置网络参数：目标误差ε、学习速率 η、学习步长t。

⑤设置LM算法相关参数初始阻尼因子μ0、进步因子φ、收敛精度ε。

⑥进行网络训练。

(3) 根据LM-BP神经网络模型求出最优设计变量水平。

4　实例证明

本文实验数据来自文献[12]的注射铸模试验。

4.1设计正交试验，收集样本数据

注射铸模机工作过程是一个复杂制造的过程，由于零件的质量受到高注射压力的影响，不同的压力注入量，生产出来的零件质量也不同。在这个过程中，以高注射压力为观测点，零件的质量是随着高注射压力变化的动态响应值。我们采用离线试验设计的方法结合LM-BP神经网络来优化过程变量的设置水平，使得零件质量变化符合生产要求。通过研究可知，注射速度、紧固时间、高注射时间、低注射时间、紧固压力、水冷却温度、低注射压力是影响零件质量的主要因素，另外注射过程还受到熔化指数、再研磨百分比、操作者、树脂湿度等噪声因子的影响。具体的实验安排如下：Y是零件的质量，观测点p为高注射压力，共有8 个观测点，分别是650 Pa、700 Pa、750 Pa、800 Pa、850 Pa、900 Pa、950 Pa、1000 Pa，实验中共包括7个两水平的可控因子，因子水平如表1所示，4个噪声因子，为了减少实验成本和实验费用，定义一个两水平的综合噪声因子(XN)来表示这些噪声因子水平，如表2所示。该实验采用27-4部分因子实验，如表3所示。

表1　注射铸模实验控制

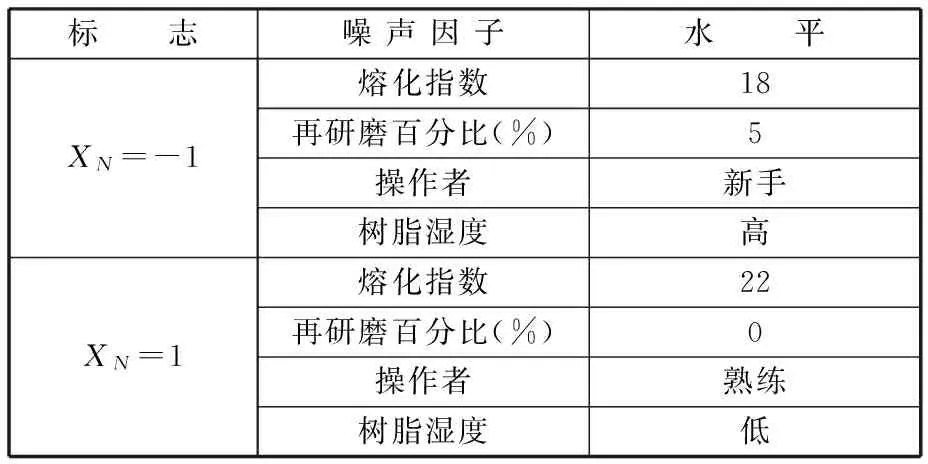
表2　注射铸模实验的综合噪声因子

实验分两天进行，第一天，将综合噪声因子设置在低水平。对每一个控制因子水平组合，在每个压力观测点上，制造并称重。第二天，将综合噪声因子设置在高水平重复前一天的过程。零件质量(响应)及其对应的压力设置(观测点)完整数据如表4所示。由表4可知，第6次实验和第14次实验输出的轮廓图都满足实验要求，即为我们的目标轮廓图，实验目的就是寻求最优的因子设置水平，使得输出轮廓图接近目标轮廓图。

表3　注射铸模实验的控制表

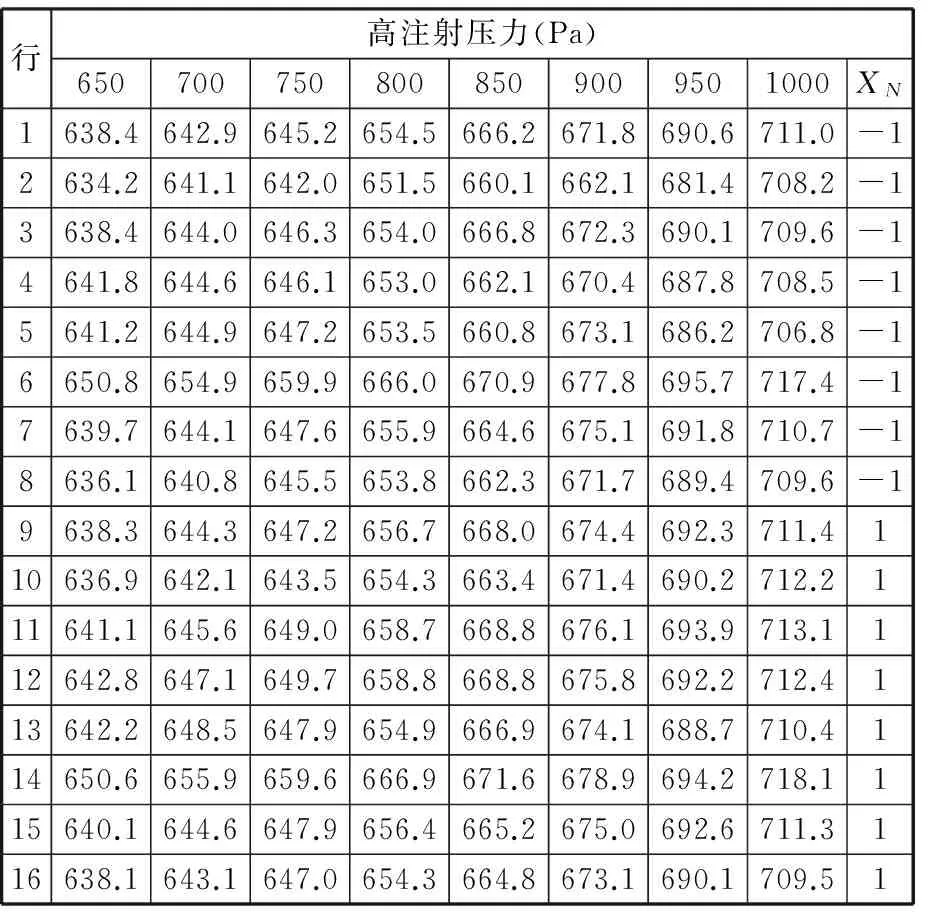
表4　注射铸模实验的响应数据

4.2确定神经网络的模型结构，优化训练神经网络

(1)准备训练样本，并对响应值归一化处理。采用表3、表4的实验数据，并利用式(4)对表4数据进行归一化处理。

(2)确定网络结构。本文采用3层BP神经网络，根据实验实际情况确定输入层、输出层节点数。轮廓图由8个观测点组成，即输入层节点数为8；可控因子和噪声因子共8个，输出层节点数为8。隐含层节点数根据式(5)计算，其可能取值为5～14，通过试凑法确定当隐含层节点数为11时，网络性能最好，所以本文神经网络模型的结构为输入层节点数8，隐含层节点数11，输出层节点数8。

(3)设定传递函数。输入层到中间层，中间层到输出层的传递函数均采用连续可微的tansig函数。

(4)设置网络参数。训练次数为1000，目标误差为0.0001，学习速率为0.1。

(5)设置LM算法相关参数：ε=0.0001，μ0=0.001，φ=10。

图2　LM-BP神经网络的误差曲线图

图3　标准BP神经网络的误差曲线图

图4　LM-BP神经网络训练参数图

(6)网络训练过程。在网络结构和参数设置都相同的情况下，用相同的训练样本分别对结构相同的标准BP神经网络模型和LM-BP网络模型进行训练，训练结果如图2所示。由图2可以看出，LM-BP神经网络在训练11步达到预设收敛精度0.0001停止训练。而标准的BP神经网络运行了3000步(图3)，不仅未达到预设收敛精度0.0001，网络还进入误差平坦区，产生局部最小点。通过比较，无论是收敛速度还是精度，LM-BP神经网络模型较于标准BP神经网络有很大的提高。同时由图4可以看出训练结束时误差曲面的梯度呈下降趋势，Mu值也呈减小趋势，验证样本的误差曲线连续3次迭代不再下降。MATLAB给出的模型拟合值R2为81.07%，说明模型拟合效果很好。综上可知，本文设计的LM-BP神经网络训练效果极佳，性能很好，可以进行下一步计算。

4.3计算最优设计变量水平

将目标轮廓图作为输入层神经元输入训练好的神经网络，得到的最优因子水平为(-0.852 76，-0.9238，0.975 28，0.878 35，-0.992 87，0.888 29，0.996 66，-0.846 54)，由于文中控制因子为离散型变量，所以最优因子组合为(-1，-1，1，-1，1，1，1，-1)。

4.4结果比较

(6)

表5　优化结果比较

5　结语

本文目的在于如何利用离线试验设计技术对函数响应进行优化。提出了一种基于LM-BP神经网络的针对输出为非线性轮廓图(non-linearprofile)的优化方法，并结合注射铸模机工作实例证明本文所提方法的合理性和有效性。首先采用正交试验表设计实验，与传统实验方法相比，本文方法具有较高的实验效率。然后，利用神经网络建模可以避免由于实验误差和试验设计方案所造成的模型系数估计误差。最后，利用LM算法对BP神经网络进行优化训练，通过阻尼因子在Gauss-Newton法和梯度下降法之间自适应调整来实现网络权值的优化，使网络能够有效地收敛，大大提高了网络的收敛速度和泛化能力，并在一定程度上克服了标准BP神经网络收敛速度慢很容易陷入局部极小的问题。本文的缺点是，利用神经网络模型拟合输入与输出之间的函数关系，其输出数值是通过内部运算得到的，由于网络各层之间相互关联，神经网络无法反推输出产生的原因。其次利用LM算法对网络进行优化训练，由于LM算法本身的复杂性，其算法参数初始值本文并未作深层次的研究，这将作为以后的研究重点继续展开。

[1]何桢,马林．六西格玛管理[M]．北京：中国人民大学出版社，2007.

[2]MontgomeryDC.DesignandAnalysisofExperiments[M]. 7thed.NewYork：JohnWiley&Sons,2009.

[3]WilliamsJD,WoodallWH,BirchJB.StatisticalMonitoringofNonlinearProductandProcessQualityProfile[J].QualityandReliabilityEngineeringInternational,2007,23(8):925-941.

[4]ZouC,TsungF，WangZ.MonitoringGeneralLinearProfilesUsingMultivariateExponentialWeightedMovingAverageSchemes[J].Technometrics, 2007,49(4):395-408.

[5]JensenWA,BirchJB.ProfileMonitoringviaNonlinearMixedModels[J].JournalofQualityandTechnology,2009,41(2):18-34.

[6]TaguchiG,WuY.IntroductiontoOff-lineQualityControlSystem[J].JournalofFoodProtection, 1979,51(6):449-451.

[7]ChickenE,PignatielloJJ,SimpsonJR.StatisticalProcessMonitoringofNonlinearProfileUsingWavelets[J].JournalofQualityTechnology, 2009, 41 (2):198-212.[8]BoxGEP,WilsonKB.OntheExperimentalAttainmentofOptimumConditions[J].JournaloftheRoyalStatisticalSociety，SeriesB,1951, 13(1):1-45.

[9]TaguchiG.IntroductiontoQualityEngineering:DesigningQualityintoProductsandProcesses[M].Tokyo:AsianProductivityOrganization, 1986.

[10]McClellandJL,RumelhartDE.ParallelDistributedProcessingExplorationsintheMicrostructureofCognition[M].Cambridge:MITPress,1986.

[11]KitaharaM,AchenbachJD,GuoQC.NeuralNerworkforCrack-dapthDeterminationfromUltrasonicBack-scatteringData[J].ReviewofProgressinQuantitativeNondestructiveEvaluation,1992,11:701-708

[12]MillerA,WuCFJ.ParameterDesignforSignal-responceSystem:aDifferentLookatTaguchi’sDynamicParameterDesign[J].StatisticalScience, 1996,11(2):122-136.

[13]HussamA.AnalysisandOptimizationofProfileandShapeResponseExperiments:[D].Pennsylvania:thePennsylvaniaStateUniversity.

(编辑王艳丽)

A Optimization Method for Non-linear Profile Based LM-BP Neural Networks

Xu JingHe ZhenYuan Rong

Tianjin University，Tianjin，300072

A method to optimize the non-linear profile was presented based on the DOE theory BP neural network model with Levenberg-Marquard algorithm, which were compared with the traditional statistical regression modeling by a example. The results show that the estimation errors of the model coefficients due to the design and experimental errors may be avoided based on LM-BP neural network modeling.Compared with the BP algorithm this method overcomes the standard BP algorithm performance of unstability, slow convergence and low convergence precision, the presence of local minima and other short-comings.The method proposed herein has a high accuracy, optimization results are satisfactory

BP neural networks； Levenberg-Marquard(LM) algorithm； design of experiment(DOE)； non-linear profile

2015-11-09

国家杰出青年科学基金资助项目(71225006)

F406.3

10.3969/j.issn.1004-132X.2016.20.010

许静，女，1982年生。天津大学管理与经济学部博士研究生。研究方向为企业管理、质量管理。何桢，男，1967年生。天津大学管理与经济学部教授、博士研究生导师。袁荣，女，1990年生。天津大学管理与经济学部博士研究生。