山地旅游布依数学文化教学案例研究

彭光明 孙 健

（兴义民族师范学院， 贵州 兴义 562400）

山地旅游布依数学文化教学案例研究

彭光明 孙 健

（兴义民族师范学院， 贵州 兴义 562400）

依托山地旅游情景和布依族文化，结合“情景—问题”教学模式和“三教”理念的培育，旨在探索中小学数学教学案例并用于课堂实践，对培养少数民族地区学生的核心素养将会收到很好的效果。

山地旅游；数学文化；教学案例；核心素养

Abstract:BasedonthemountaintourismsituationandtheBuyiculturalbackground,combinedwiththe“Scene-Question“teaching model and“Three kinds of Education"educational ideas,this paper aims to explore the case of middle school and primary school mathematicsteachingforclassroompractice.Thisexplorationwillhaveagoodeffectonthecorequalityofstudentsinminorityareas.

Key words:mountain tourism;mathematical culture;teachingcase;core literacy

一、问题提出

黔西南州地处祖国大西南，是典型的喀斯特地区，又是布依族聚居地，州内有着美丽丰富的山地旅游资源和独特的布依族传统文化。州内有许多著名的旅游目的地，如被誉为“地球上美丽的伤疤”的马岭河峡谷、被著名地理学家徐霞客赞叹为“天下山峰何其多，唯有此处峰成林”的万峰林、“高原平湖明珠”万峰湖、“史迪威公路形象标识”二十四道拐、“大地圣母”双乳峰等；此外，布依族的传统建筑、服饰和生产生活用具中也体现出浓郁的民族文化，它们都体现了本地人民的智慧。在这些旅游资源和民族文化资源中，蕴含着众多的数学文化。通过教师的开发整理，它们都可以成为中小学数学教学的情境。

现在通用教材中的数学情境主要以主流地区的文化背景为主，由于地域和文化差异，少数民族地区学生没有切身的感受，所以觉得数学学习过程很枯燥、很抽象。为解决这个问题，让学生在学习数学的过程中享受自然美，感受家乡美，结合我校“地方性、民族性、师范性”特色，经过论证和思考，决定利用本地旅游资源和民族文化资源为情境，编写反映地方特色的数学教学案例，并用于中小学实际课堂教学，以尝试突破当前数学课堂教学远离生活、枯燥无味的困境。

二、案例编写原则

新课标指出，数学教学要紧密联系学生的生活实际，从学生生活经验和知识出发，创设生动有趣的数学情景，引导学生开展观察、操作、猜想、推理和交流互动，让学生经历知识的形成与发生过程。心理学家罗杰斯也说过：真实的问题情境和活动是最能引起态度和个人情绪的学习方式。所以，在数学课堂教学中，尽可能利用学生身边的场景和他们熟知的文化背景作为学习知识的切入点，围绕以下几个原则编写教学案例。

1.以旅游情景为依托，以民族文化为抓手。

教学案例要突出旅游情景或民族文化背景。通过介绍学生身边的旅游情景，吸引学生的学习注意，让学生感觉置身于美丽的风景之中，迫切展开一段美好的旅程，达到“良好的开端是成功的一半”的目的；另一方面，教育的本质是优秀文化的传承与知识、技能和态度的获得。因此在少数民族地区进行数学教育，除传承中华文化以外，还应传承地方少数民族文化。在数学教学中渗透地方民族文化是少数民族学生获得适应本民族优秀文化、主流文化必须的知识、技能和态度的主要途径[1]。同时以学生日常生活中的具有民族特征的建筑、服饰、工具等引入数学知识，学生心理有认同感，产生强烈的学习动机。

2.以数学问题为导向，以数学应用为归宿。

数学问题是将情境与数学知识联系起来的桥梁，因此，提出的数学问题必须要有很好的导向性，要能准确诠释情境中的数学元素。为防止学生思维“跑偏”，教师可预设一些数学问题，引导学生找出其中的数学关系， 提出新的数学问题。但案例不能因“问题”而“情境”，要以数学应用为归宿。它有两方面的含义，首先，通过问题解决过程，学生学会探究和创新，最终获得数学应用能力；其次，教学案例只有通过课堂实践，才能测试其有效性和可行性，并结合师生的评价与反馈，不断修改完善，最终形成能提高课堂教学效率的校本教材，这是案例编写的最终归宿。

3.以“三教”理念为指导，以核心素养为宗旨。

“三教”理念是指教思考、教体验、教表达，三者是有机的整体，相互涵摄，“三教”理念给我们如何在学科教学中培育学生的核心素养提供了指引[6]。教学案例最终是要用于课堂教学实践，所以案例设置的数学情境、预设的问题和解决问题的方法，都要足以引起学生多角度的思考，能让学生清楚表达出其中的数学关系，提出自己的问题，能通过探讨解题过程，获得成功学习的体验。

用这种独具特色的数学教学案例进行教学，学生容易理解数学知识与现象之间的内在联系，这是激发大脑内在能量和刺激逻辑——数学智能的重要方法[3]。在此过程中，引导学生提出问题，探究解决问题的模式，强化解决问题的技能，培养灵活的思维，改进学习态度等环节，都能很好地贯彻培养学生核心素养的理念，是实施数学创新教育和培养学生创新能力的有效方法。

三、案例编写模式

教学案例的本质是地方教材或校本教材，既然是以教学素材的形式出现，就应该有一定的模式。课题组把每个案例按顺序分成6个模块，即旅游情景（或民族文化）→知识点→数学情境→数学问题→问题解决→教学思考。

旅游情景（或民族文化）采用图文并茂的方法，介绍某个旅游景点（或民族文化现象），让学习者产生耳目一新的感觉，同时也有推介旅游和传授民族文化知识的作用；在指明案例所涉及的数学知识后，结合教材知识，创设生动有趣的数学情境；对于数学问题模块，教学案例中预设一些导向性强的问题，在实际教学过程中，可由浅入深引导学生提出数学问题，并以预设问题或学生提出的问题作为任务驱动，启发学生逐一解决问题；最后，教师用简短的文字陈述本案例在核心素养培育、数学方法指导、引导学生思考、引导学生表达等方面的教学想法和反思。

四、案例展示

案例一 万峰湖游船行驶问题

旅游情景：万峰湖（图1）位于贵州省兴义市南面，距兴义市24公里。享有“万峰之湖，西南之最，南国风光，山水画卷”之美誉。景区以红椿坡阳口内湖景观为主，景观面积50平方公里。它的主要景点有红椿水上石林、马岭河坡阳入湖口、水上布依山寨等。景区气候宜人、四季可游，融山、谷、湖、林于一体，即能乘船畅游、又可临湖垂钓，还能体验浓郁的民族风情，是难得的旅游度假好去处。

图1

图2

图3

知识点：解直角三角形、二次函数求极值

数学情境：A、B两船分别从东西两个方向的红椿码头（图2）、吉隆堡（图3）两地同时出发，且红椿码头在吉隆堡的正东方向且相距5km，A从红椿码头自东向西行驶，B从吉隆堡自北向南行驶，A船的速度是8km/h，B船的速度是6km/h，数学问题：

问题1：x小时后，B行驶的距离是多少？

问题2：x小时后，A与吉隆堡之间的距离是多少？

问题3：两船行驶的路线构成什么图形？

问题4：什么时候两船的距离最短，最短距离是多少？

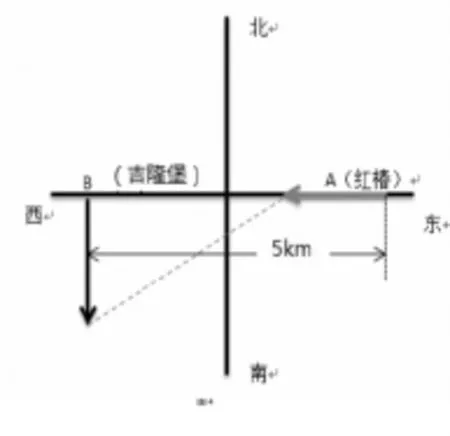
图4

问题解决：

问题1：x小时后，B行驶的距离是

问题2：x小时后，A与吉隆堡之间的距离是5-8x

问题3：两船行驶的路线构成直角三角形（图4）

教学思考：

1.核心素养培育

二次函数模型建立。新课标明确提出，数学课程应提供基本内容的实际背景，反映数学的应用价值，开展“数学建模”的学习活动，应力求使学生体验数学在解决实际问题中的作用，促进学生逐步形成和发展数学应用意识，提高实践能力。本例通过二次函数的应用，培养学生学会建立数学模型的思想。

2.数学方法指导

函数求极值。本例通过设置数学情境，让学生学会通过建立数学模型解决实际问题，并进一步掌握二次函数求最值的方法。

3.引导学生思考

本例可通过教学思考，如改变船的位置方位，还能构造出其它的解斜三角形的案例，引发出其它数学问题，并教会学生一题多变、一题多思，学会举一反三。

4.引导学生表达

教学中根据身边的旅游景点，引导学生口头或文字表达：最值问题如何求？二次函数求极值有哪些方法？如何从情境中提出问题？如何解决实际问题？等等。

案例二 二十四道拐汽车行驶问题

旅游情景：晴隆二十四道拐，是抗战公路——“史迪威公路”的形象标识（图5）。古称“鸦关”，雄、奇、险、峻，有一夫当关，万夫莫开之势。从山脚至山顶的直线距离约350米，垂直高度约260米;在倾角约60度的斜坡上以“S”型顺山势而建，蜿蜒盘旋至关口，全程约4公里。2006年国务院公布为第六批全国重点文物保护单位，是“金州十八景”之一。

图5

图6

知识点:不等式――比较大小

数学情境：国际山地旅游大会在美丽的二十四道拐举行汽车拉力赛（图6），甲、乙两车从二十四道拐的第一拐出发，到达第二十四道拐。甲车有一半的时间以速度m行驶，另一半时间以速度n行驶；乙有一半路程以速度m行驶，另一半路程以速度n行驶。

数学问题：

问题1:甲车到达终点的时间是多少？问题2:乙车到达终点的时间是多少？

问题3:甲、乙两车谁先到达第二十四道拐？问题解决：解:设第一拐与第二十四拐的路程为S，甲、乙两车行驶完这段路程所需时间分别为t1t2，根据题意得：

由于 m，n，s均为正数，且 m≠n，

∴t1-t2＜0，即 t1＜t2，故甲车先到达终点。

那么，备受青睐的“粮食银行”究竟有什么特点呢？一是存取自由。“粮食银行”存取时间通常为一年，期间粮权不变，可以随时提取存粮或兑现。二是保值增值。农民存粮后可以直接提取现金，也可以根据市场价格变化随时进行结算。如果市场价格上涨，就按上涨价格结算，粮价下跌时可按照存入量兑换等值的粮油产品。三是与便民连锁店联网，兑换方便。农民凭“存折”可到粮食系统开设的“粮油超市”兑换不同品种的粮油或其他商品。

解法二：作商法：

∴t1＜t2故甲车先到达终点

教学思考：

1.核心素养培育

构造不等式。通过设置数学情境，让学生进一步掌握时间、速度、路程三者的数量关系,即，提升对路程、速度、时间三者关系模型的再认识，同时进一步明白如何将纯粹的数学问题具体化，通过不等式的应用，进而增强学生解决实际问题的能力。

比较法。通过实际应用，掌握比较两个数大小的方法，即作差法和作商法。

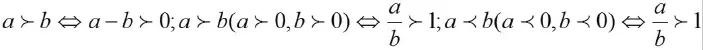
3.引导学生思考

引导学生通过思考，为何车辆到达与m、n的值无关。均值不等式和放缩法什么时候用，怎样应用？体现了一题多证的思想，拓宽解题思路。以二十四道拐为背景，既了解了抗战历史知识，又获得了数学知识，学在其中乐在其中。

4.引导学生表达

让学生总结比较两个数的大小的方法，描述解题步骤，掌握如何使用均值不等式和放缩法。

五、结束语

结合中小学生数学学习内容，挖掘黔西南州山地旅游情景和布依族传统民族文化中的数学元素，利用学生熟悉的场景编写成教学案例，并用于数学课堂教学，对改变地方资源融入数学教育存在的“高评价低应用”现象、提高现实数学教育的可操作性以及培养学生核心素养等方面都将起到很好的作用。

[1]付茁.对我国少数民族数学教学中渗透本民族优秀文化的思考[J].数学教育学报,2009,18(5):35-37.

[2]吕传汉,汪秉彝.再论中小学“数学情境与提出问题”的数学学习[J].数学教育学报,2002,11(4):72-76.

[3]陈朝东,蒋秋,张阳开.中国小学数学教科书中少数民族元素的渗透探析 [J].数学教育学报,2014,23(5):51-55.

[4]张和平.苗侗民族地区地方数学课程资源开发模式构建[J].教学与管理,2012(1):102-103.

[5]孙健.对布依族民族数学教学案例编写的思考[J].兴义民族师范学院学报,2015（4）:72-78.

[6]孙兴华.基于“三教”理念的儿童数学核心素养培育策略[J].兴义民族师范学院学报,2016（3）:104-108.

责任编辑：王美娜

Studyonthe TeachingCase ofthe MathematicalCulture inBuyiNationalityinMountainTourism

PENG Guang-ming SUN Jian
（Xingyi Normal Universityfor Nationatities,Xingyi,Guizhou 562400,China）

1009—0673（2016）06—0001—05

G752

A

2016—12—10

贵州省教育厅2014年专业综合改革项目：数学与应用数学（卓越城乡数学教师培养），黔教高发【2014】378号。

彭光明（1969— ），男，贵州晴隆人，兴义民族师范学院数学科学学院教授，研究方向：课程与教学论。