基于半定松弛的到达时差定位算法

吴　盖

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，陕西 西安 710071)



·工程应用·

基于半定松弛的到达时差定位算法

吴盖

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，陕西 西安 710071)

针对到达时差定位系统，提出了一种新的基于半定松弛的时差定位算法。该方法首先将距离测量误差作为一项重要参数，在到达时差测量模型下，建立了一个关于定位估计的非凸优化问题，然后通过松弛约束条件将该非凸优化问题转换成等价的凸优化问题，运用凸优化理论中的半定松弛规划方法求解目标的位置。仿真实验结果表明，该方法可以有效降低定位误差。

到达时差；凸优化；半定松弛；定位误差

0　引言

多站时差定位系统具有较高的定位精度，近年来得到了快速发展，并已广泛应用于雷达、声纳[1]、无线传感器网络[2]等领域。根据定位利用的信息不同，无源定位可以分为三角定位、交叉定位和时差定位等。其中多站时差定位又称为双曲线定位，该方法具有定位速度快、精度高的优点，因而被广泛应用于各领域。

非线性方法和线性方法[3]是解决时差定位问题的两种常见方法。非线性理论的思路是尝试直接求解出目标辐射源的位置，它包含非线性最小二乘估计(NLS)和极大似然估计(ML)[4]。线性定位原理的基本思路是把非线性方程转化为线性方程组再进行求解。通常，相比而言，非线性方法具有更高的定位精度。但是由于代价函数是多峰值的，常用的非线性方法不能保证全局性的收敛。然而线性方法经过线性优化的代价函数是单峰的，就能够保证获得全局解，并且该方法计算量较小，但随着测量误差的增大，该方法的性能也会急剧下降[5]。本文提出的基于半定松弛(SDR)的到达时差定位方法能够平衡线性和非线性这两种方法，也就是说，该方法同时具有精度高和全局收敛的优点。该方法先将NLS或者ML估计问题转化为一个等价的约束优化问题，然后松弛约束条件得到一个凸的半定规划问题。松弛后的凸优化问题易于求解且具有唯一的全局最优解。最后通过仿真实验验证了该定位算法的有效性。

1　问题描述

假设时差定位系统共有L(L≥4)个观测站，各观测站的坐标为：Xl=[xlyl]T,l=1,2,…,L。以观测站X1作为整个时差定位系统的参考站。目标辐射源的位置为X=[xy]T。目标辐射源同各个观测站之间的径向距离记为dl，其表达式为：

dl=‖X-Xl‖=((x-xl)2+(y-yl)2)1/2,l=1,2,…,L

(1)

式中, ‖·‖表示向量的二范数。

那么从TDOAs得来的径向距离差为:

(2)

式中,ql是径向距离的误差，它与时间差的误差成正比。

由式(1)、式(2)可以得到:

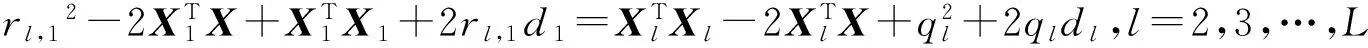
(3)

又由式(1)可知dl=rl,1+d1-ql，代入式(3)可消去变量dl：

(4)

将式(4)写成矩阵形式[6]：

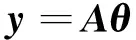
(5)

式中,

(6)

(7)

X=[X1-X2X1-X3…X1-XL]T

(8)

Pr=[diag(r)-r]

(9)

r=[r2,1r3,1…rL,1]T

(10)

P±=[±IL-1]

(11)

q=[q2q3…qLd1]T

(12)

Q=qqT

(13)

注意QL,L与X有关。

(14)

式中，R=XTX。

由于ql为径向距离的误差，在误差平方最小准则下，并考虑到上述约束关系，则目标位置估计问题可以描述为如下的优化公式:

(15)

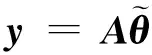
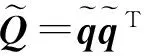
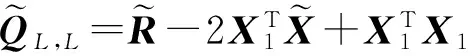
(16)

2　基于半定松弛的到达时差定位算法

SDR是求解非线性非凸优化问题的一种精确近似方法，并且对于许多非凸的优化问题，这种近似解法往往可以得到原优化问题的最优解。优化问题式(15)、(16)实际上是一个非凸的等式约束优化问题，本节采用半定松弛方法对该问题进行求解。

根据矩阵迹的性质XTAX=tr(XTAX)=tr(XXTA),则式(15)有如下等价：

(17)

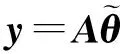
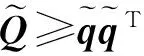
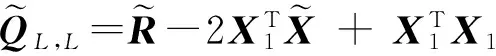
(18)

在凸优化理论值，式(16)是一个SDR问题。事实上，求解此类问题方法很多，本文提供一种方法：可以在Matlab中使用凸优化工具箱CVX来求解[7]。

3　仿真实验

本节分别就近场目标u1=(200,300)和远场目标u1=(1500,1600)，对基于SDR的时差定位算法进行了仿真分析。仿真实验中共设置了4个观测站，3个副站以主站为中心成Y型分散，各副站到主站的距离为500m。主站及3个副站的坐标分别为(0,0)、(500,0)、(-250,433)、(-250,-433)。各观测站及目标u1，u2的位置如图1所示。

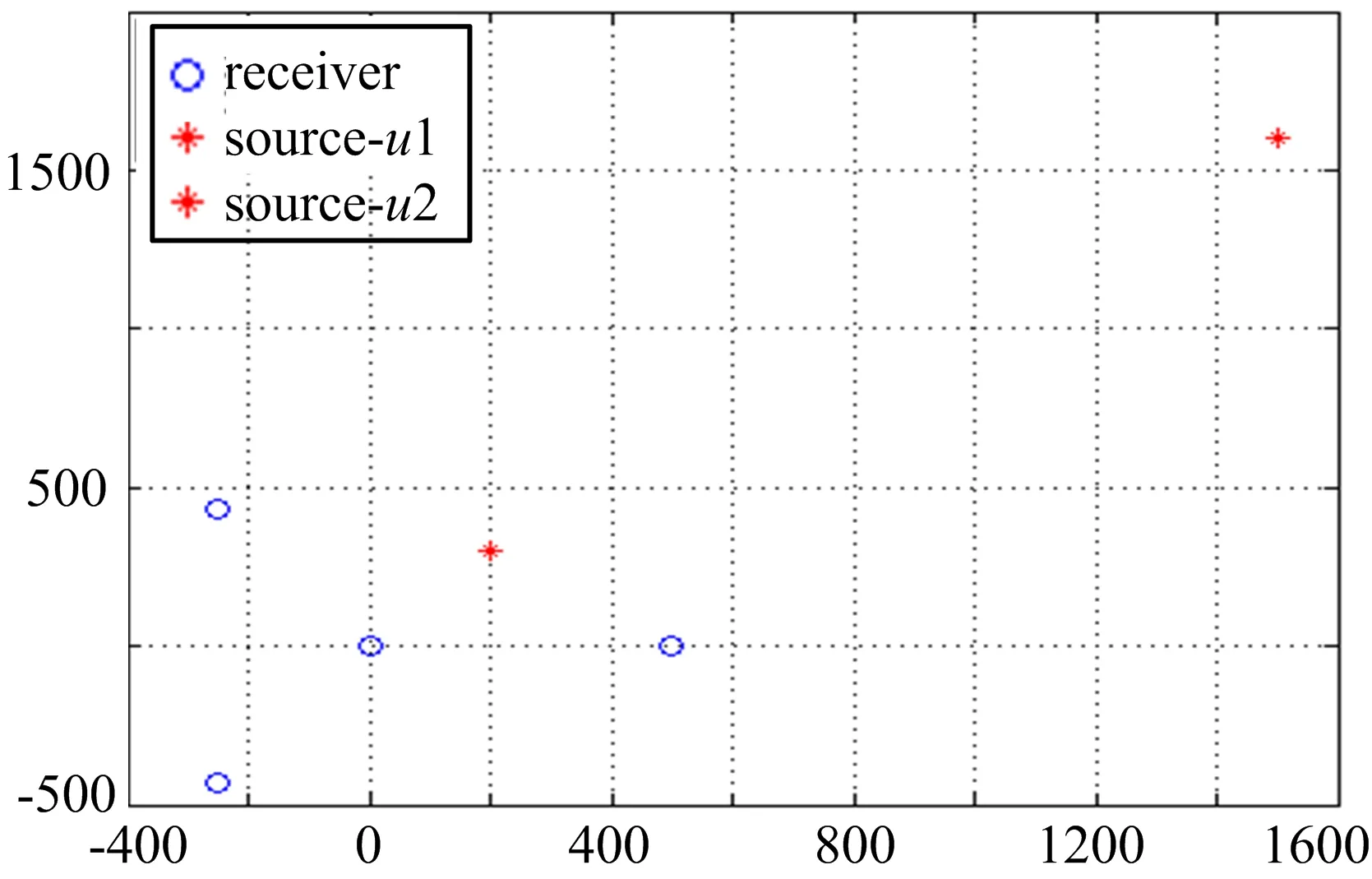
图1　观测站及目标的位置

实验中设定由时差误差造成的径向距离误差ql为零均值高斯分布，其协方差矩阵的主对角线元素的值为σ2，各副站之间的径向距离误差是相互独立的。通过改变σ2的精度，得到算法在不同测量误差情况下的定位性能。共进行了200次独立统计实验，并统计位置估计的均方根误差RMSE。图2为ML、线性最小二乘法(LLS)[8]以及本文所提的SDR解法对近场目标的位置估计RMSE曲线，图3为上述3种算法对远场目标的位置估计RMSE曲线。

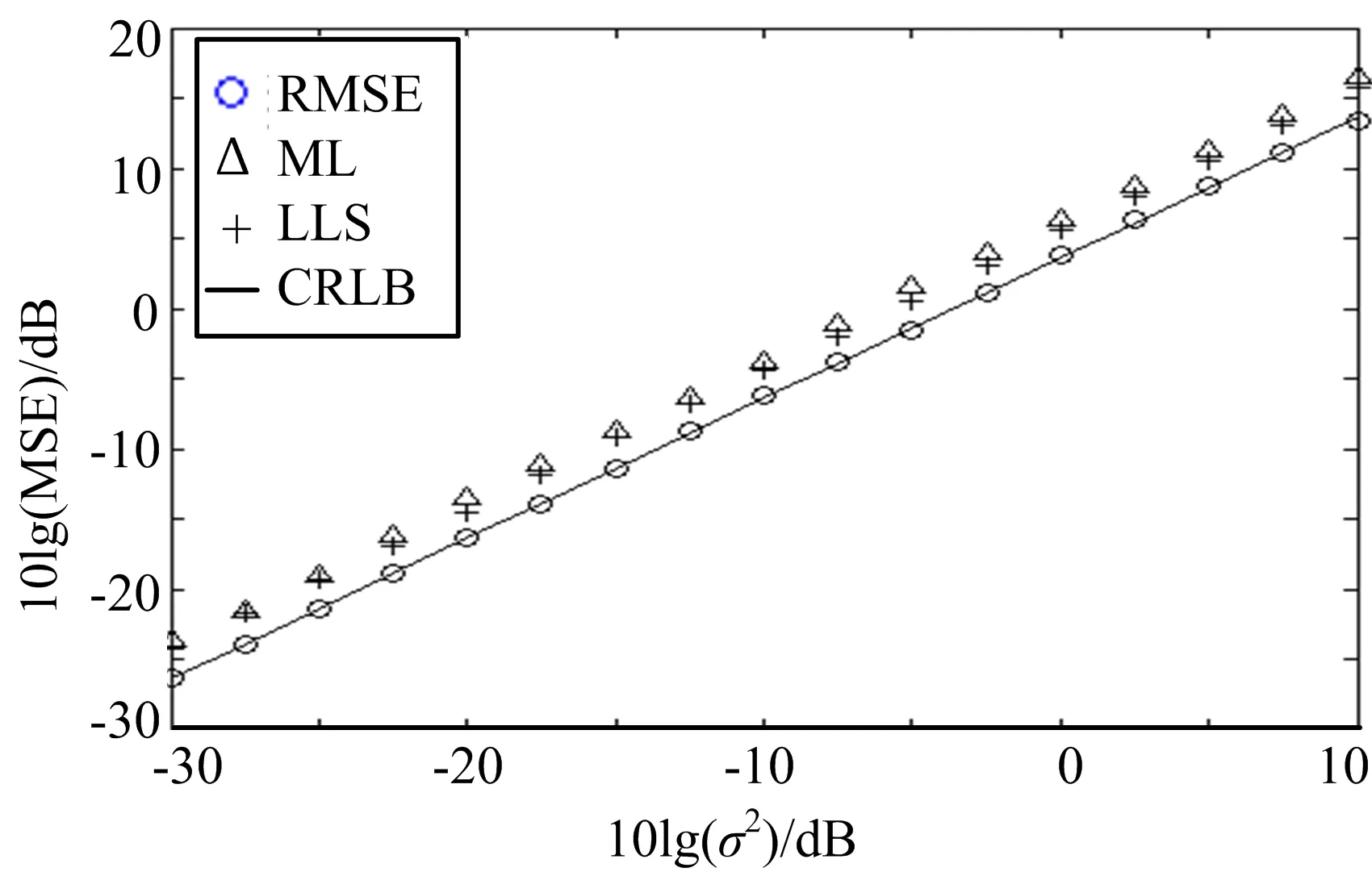
图2　对近场目标的定位RMES曲线

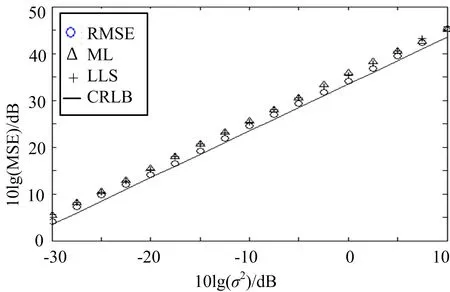
图3　对远场目标的定位RMES曲线

从仿真结果中可以看出，SDR方法主要有ML算法以及LLS算法。 从图2可以看出， 在近场情况下，SDR算法达到了定位的CRLB。对于远场目标，虽然SDR算法性能有一定的下降，但相对于另外两种算法仍然具有较小的定位RMSE。同时从图2和图3可以看出，在实验条件下，随着σ2的增大，定位误差会越来越大。

4　结束语

本文针对到达时差定位系统，提出了一种基于SDR的定位算法，该方法将关于目标位置求解的非凸优化问题松弛为一个可以有效求解的半定规划问题，并且在仿真中发现松弛后的优化问题总是能够得到原问题的最优解，这就证实了该方法的有效性、稳定性和实用性。■

[1]Carter GC.Coherence and time delay estimation: an applied tutorial for research, development, test, and evaluation engineers[C].New York: IEEE, 1993.

[2]Ilyas M, Mahgoub I.Handbook of sensor networks: compact wireless and wired sensing systems[M].London, UK: CRC Press, 2005.

[3]So HC.Source localization: algorithms and analysis[M]∥Handbook of Position Location: Theory, Practice and Advances.Wiley-IEEE Press, 2011.

[4]任源博.多星时差无源定位系统研究[D].西安电子科技大学,2014.

[5]Cheung KW, So HC, Ma WK, et al.A constrained least squares approach to mobile positioning: algorithms and optimality[J].EURASIP Journal on Advances in Signal Processing, 2006:1-23.

[6]Chan KW, So HC, Ma WK, et al.A flexible semi-definite programming approach for source localization problems[J].Digital Signal Processing, 2013,23:601-609.

[7]Luo ZQ，Ma WK． Semi-definite relaxation of quadratic optimization problems[J]． IEEE Signal Processing Magazine,2010，27(3):20-34．

[8]So HC.Source localization :algorithms and analysis[D]．Department of Electronic Engineering, City University of Hong Kong,2012:44-48.

TDOA location method based on the semi-definite relaxation

Wu Gai

(Key Laboratory of Electronic Information Countermeasure and Simulation,Ministry of Education, Xidian University, Xi’an 710071, Shanxi, China)

A new TDOA location method based on the semi-definite relaxation is proposed.Firstly, the distance measuring error is a very significant parameter to be utilized to establish a nonconvex optimization problem about localization estimation.Then, the nonconvex optimization problem is converted to the equivalence convex optimization problem, and the target localization is solved by using semi-definite relaxation programming method based on convex optimization method.Simulation results show that the proposed approach is effective.

TDOA; convex optimization; semi-definite relaxation; location error

2015-06-15

吴盖，男，硕士，主要研究方向为定位技术。

TN971

A