基于K—means算法的文本分类技术研究

王健

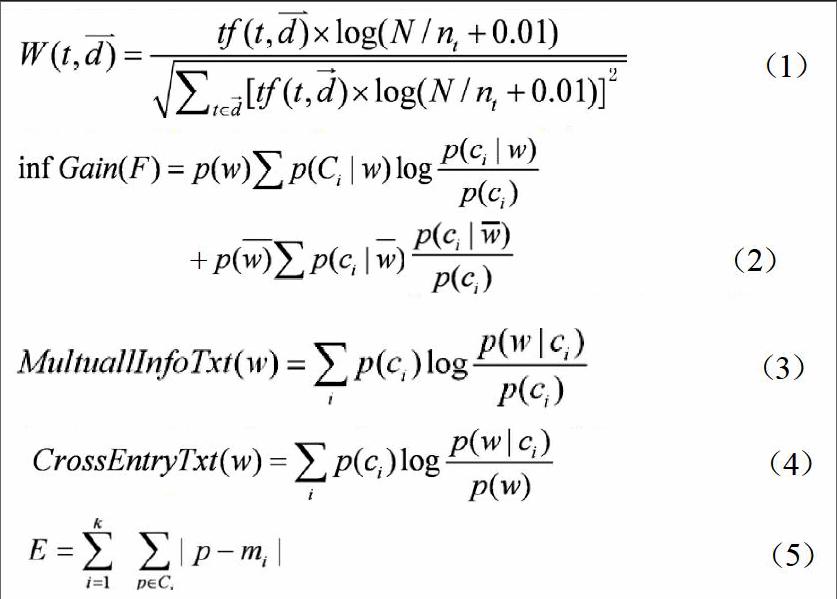
摘 要 文本分类技术是网络信息挖掘中内容挖掘的重要手段之一，通过文本的分类技术可以将网络中纷繁复杂的信息分门别类的组织在一起，从更深的层次来寻找文档之间的联系本文，阐述了基于K-means算法的文本分类的关键技术，从网页的解析、文本的表示、降维技术到分类算法进行详细的论述，并对两个K-means算法做了改进。

关键词 文本分类 降维技术 文本表示 分类算法

中图分类号：TP393 文献标识码：A

文本分类是指在给定分类体系下，根据文本内容自动确定文本类别的过程，将大量的文本归到一个或多个类别中。从数学角度来看，文本分类是一个映射的过程，将未标明类别的文本映射到己有的类别中来，数学表示如下：f：A->B 其中A为待分类的文本集合，B为分类体系下的类别集合。

文本分类技术是网络信息挖掘中内容挖掘的重要手段之一，通过文本的分类技术可以将网络中纷繁复杂的信息分门别类的组织在一起，从更深的层次来寻找文档之间的联系，不只停留在字面的匹配上。文本分类技术应用于信息检索中有利于提高检索的正确率和准确率。

1网页的解析

按照W3C组织所制定的标准，每一个HTML页的结构都可以对应地描述成DOM树的形式。DOM定义了HTML文档的逻辑结构，提供了一种对网页中的数据及内容进行管理和操作的途径。DOM将整个文档的内容分别抽象为不同的对象，用结点的形式予以表示，如标签结点、文档类型结点、文本结点、注释结点、属性结点等。再用类似于父子的关系将各结点按照不同层次有顺序地组织起来，形成树型结构。

2文本表示

向量空间模型（Vector Space Model，简记为VSM）是一种较著名的用于文档表示的统计模型，该模型以特征项做为文档表示的基本单位，特征项可以由字词或短语组成。每一个文档可以看成是由特征项组成的n维特征向量空间的一个向量：D=（T1，W1；T2，W2；T3，W3……；Tn，wn），其中Wi为第i个向量Ti在文档中的权重，一般选词做特征项比选字做为特征项要好一些。一般使用TF-IDF公式计算特征项权重，其中TF（Term Frequency）表示词频，IDF（Inverse Document Frequency）表示逆文档频率，反映文档集合中出现该特征项的文档数目的频率，TF-IDF权重公式如公式（1）所示：

3降维技术

3.1信息增益

信息增益在机器学习中经常被用做特征词评判的标准，它是一个基于熵的评估方法，定义为某特征项在文档中出现前后的信息熵之差。根据训练数据计算出各特征词的信息增益。删除信息增益很小的词，其余的按信息增益从大到小排列。如果以信息增益最大者为要根结点，建立一个决策树就可以进行决策树的分类挖掘。如公式（2）所示。

其中i=1，2…M。p（ci）表示类文本在语料中出现的概率，p（ci|w）表示文本包含特征项W时属于ci类的条件概率，p（w）表示语料中不包含特征项W的文本的概率，p（ci|w）表示文本不包含特征项W时属于ci类的条件概率，M为类别数。

3.2互信息（MI）

应用在相关词统计建模中，在统计学中用于表示两个变量间的关系，其计算如下公式（3）所示：

显然当特征项W独立于ci时它同该类的相关度为0 ，p（w）越小而同时p（w|ci）越大时特征项W提供类别ci的信息量越大，则这个特征项越能代表这一类，反之，p（w）越大的同时p（w|ci）越小，则可能得到负的互信息值，这种情况下，该特征项对分类的意义同样很大。

3.3交叉熵（expected cross entropy）

与信息增益类似也是一种基于概率的方法，但只计算出现在文本中的特征项，其计算如公式（4）所示：

4分类算法

K-means算法是应用最广泛的聚类算法之一，是一种已知聚类类别的聚类算法。指定类别数k，对样本集合进行聚类，聚类的结果由k个聚类中心来表达。相似度的计算根据一个簇中样本的平均值（被看作簇的中心）来进行。

首先，随机选择k个对象，每个对象初始的代表了一个簇的平均值或中心。对剩余的每个对象，根据其与各个簇中心的距离，将它赋给最近的簇。然后重新计算每个簇的平均值。这个过程不断重复，直到准则函数收敛。通常，采用平方误差准则，其定义如下：

这里的E是数据库中所有对象的平方误差的总和，p是空间中的点，表示给定的数据对象，mi是簇Ci的平均值（p和mi都是多维的）。这个准则试图使生成的结果簇尽可能的紧凑和独立。下面是K-means过程的概述。

输入：聚类的数目k和包含n个对象的数据库。

输出：k个聚类簇，使平方误差准则最小。

（1）任意选择k个对象作为初始的聚类簇中心；

（2）重复；

（3）根据聚类簇中对象的平均值，将每个对象（重新）赋给最相似的聚类簇；

（4）更新聚类簇的平均值，即计算每个簇中对象的平均值；

（5）直到不再发生变化。

这个算法尝试找出使平方误差函数至最小的k个划分。当结果簇是密集的，而簇与簇之间区别明显时，它的效果较好。对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度是O（nkt），其中，n是所有样本的数目，k是聚类簇的数目，t是迭代的次数。通常的k<

但是，K-means只有在簇的平均值被定义的情况下才能使用。这使得它不适用某些应用，例如涉及到分类属性的数据。要求用户必须事先给出k，可以算是该方法的另一个缺点。同时K-means不适合发现非凸面形状的簇，或者大小差别很大的簇。而且，它对于“噪声”和孤立点数据是敏感的，少量的该类数据能够对平均值产生极大的影响。

参考文献

[1] 高洁，吉根林.文本分类技术研究[J].计算机应用研究，2004（3）：23-25.

[2] 高倬贤.中国图书馆图书分类法与日本十进分类法比较研究[J].图书馆学研究，1999（6）：23-31.