基于熵权法的公路货运量组合预测

詹　斌，吕腊梅，黄　馨

（武汉理工大学　交通学院，湖北　武汉　430061）

基于熵权法的公路货运量组合预测

詹斌，吕腊梅，黄馨

（武汉理工大学交通学院，湖北武汉430061）

由于仅采用单一模型进行预测很难得到有效的预测结果，为了充分利用各种预测方法所提供的信息，规避单一模型的局限性，尽可能科学有效地预测公路货运量，在多元线性回归模型、二次指数平滑法以及GM（1，1）模型这三种单一模型的基础上，建立基于熵权法确定权重的组合预测模型。实证结果表明，与单一的预测方法相比，组合预测模型能够降低单一模型的预测风险，减少预测的系统误差，提高预测精度，具有较好的实用价值。

公路货运量；熵权法；组合预测

1　引言

公路货运量预测方法大致可以分为两类，一类是定性预测，它是根据已掌握的历史资料和直观材料，运用个人经验和分析判断能力，对事物的未来发展做出性质和程度上的判断，强调对事物发展的趋势、方向和重大转折点进行预测。如专家会议法、德尔菲法等，定性预测主观性较强，预测结果完全依赖于参与预测人员的经验和能力［1］。另一类是定量预测，定量预测分两种，基于时间序列的预测法和基于影响因素的预测法。基于时间序列的预测法包括指数平滑法、灰色系统法、神经网络法、小波分析法等；基于影响因素的预测法包括回归分析法、弹性系数法、投入产出法等。在进行预测时，单独采用某一种模型往往有其局限性，例如：基于时间序列的预测法以时间作为单一的预测因素，无法反映预测对象的实际影响因素，尤其是无法反映经济政策和发展速度调整等外部因素调整所引起的运输需求的变化；如果预测对象在所研究的时间序列上波动较大，预测效果就会很差。基于影响因素的预测法中，自变量或因变量未来值的选择影响预测的准确性，对数据信息的完备性要求高，而在实际预测时，很难获取充足的数据信息。因此，为了充分利用各种预测方法所提供的信息，规避单一模型的局限性，尽可能地提高预测精度，本文在多元线性回归模型、二次指数平滑法以及GM（1，1）模型这三种单一模型的基础上建立组合预测模型，根据熵权法确定各单项预测方法的权重，从而达到提高预测精度的目的。

2　预测方法

2.1单项预测模型

2.1.1线性回归预测模型。线性回归预测模型在货运量预测中应用较为普遍，它是从事物变化的相关关系出发进行预测的一种方法，其可靠性高，实用价值高。线性回归预测有一元线性回归分析、二元线性回归和多元线性回归分析。本文采用的是多元线性回归模型。

多元线性回归模型为 Y=β0+β1X1+β2X2+...+ βkXk+φ，其中φ为随机项。

在进行线性回归预测时，通常要对模型进行检验。多元线性模型的检验包括拟合优度检验、F检验、t检验、序列相关性检验。拟合优度检验一般用判定系数R2实现，0＜R2＜1，且R2越接近1，表明模型对观测数据拟合程度越高，通常，R2＞0.8时，则可以认为模型拟合程度较高。判定系数R2的计算公式为：

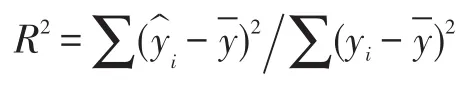
F检验按给定的显著性水平，若F＞Fα（m，n-m-1），拒绝原假设，反之，则接受原假设，说明自变量与因变量线性关系不显著。F检验的计算公式：

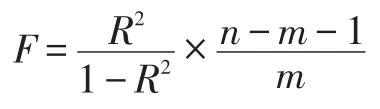
t检验，t统计量的计算公式为：

式中Cjj为矩阵主对角线上的第j个元素。

序列相关性检验，最常见的序列相关性检验是一阶自相关检验，即εi与εi+1相关，而一阶自相关检验最常用的检验方法是DW检验法，DW统计量计算公式为：

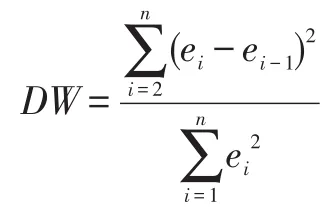
2.1.2指数平滑法。指数平滑法是用平滑系数对时间序列的历史数据进行加权修匀，建立指数平滑数学模型进行预测的方法，即对实际值和预测值分别给以不同的权重，计算加权平均数作为下期的预测值。该方法只需要最近一期的货运量预测数和实际货运量即可预测下一期的数值货运量，预测方法简单，因此在实际工作中得到了广泛应用［2］。

指数平滑法包括一次指数平滑法、二次指数平滑法和三次指数平滑法。本文采用的是二次指数平滑法，二次指数平滑法是以相同的平滑系数，对时间序列进行两次平滑修匀，使长期趋势更清楚地显示出来，然后根据两次平滑数列建立线性趋势预测模型。其计算公式如下：

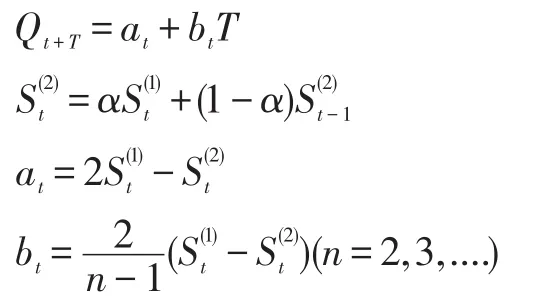
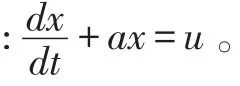
采用GM（l，1）模型进行预测时，为了保证预测精度，需对模型的精度进行检验，如果模型不能达到精度要求，那么需要对模型进行校正，常用的模型检验方法有残差检验、关联度检验、后验差检验。本文采用的是后验差检验。计算均方差比值C以及小误差概率P。P，C等级参照表1。

用下式计算后验差比值C及小概率误差P：

表1　P，C等级参照表

2.2组合预测模型

2.2.1组合预测原理。组合预测法是指对两种或两种以上预测方法的预测结果进行加权组合，与单一的预测方法相比，组合预测法更加科学合理，它能达到取长补短的效果，从而提高预测结果的精度和可靠性。

2.2.2权重确定。本文采用基于信息熵的组合预测模型。该方法引入了信息论中的信息熵概念，根据每个单项预测模型在系统中的信息熵，为各个单项预测方法在组合预测系统中赋权值，由此建立一个能够全面考虑到各种单项预测方法所提供的信息的组合预测模型，达到客观、准确的对货运量进行预测的效果。基于熵权的权重计算具体步骤如下：

设对m种预测方法用n个效果评价（误差）指标去评价，得到评价矩阵：

yij表示第i种预测方法用第j个指标进行评价得到的评估值。

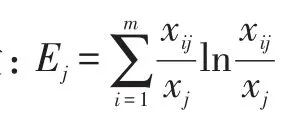
最后，计算各预测方法的权重：

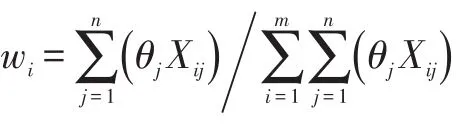
2.3模型评价

评价效果这里选择平方和误差SSE、平均绝对误差MAE、均方误差MSEA、平均绝对百分比误差MAPE、均方百分比误差MSPE这5种误差指标。

3　实例分析

本文以湖南省公路货运量为例进行组合预测，表2是2002-2013年湖南省公路货运量数据。

表2　湖南省2002-2013年公路货运量统计表［4］（单位：万t）

（1）多元线性回归预测。通过计算各经济指标与湖南省公路货运量的灰色关联度，选择了社会零售总值（x1）、地区生产总值（x2）、全社会固定资产投资（x3）作为解释变量，利用SPSS软件对公路货运量进行回归分析，建立多元线性回归模型，其预测模型为：

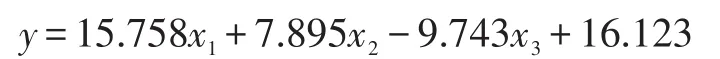
回归模型检验：对模型进行拟合优度检验，该模型的拟合优度R2=0.984，说明该模型的拟合度很高；对模型进行显著性检验，F=221.767，F0.05（1，10）=4.96，F＞F0.05，所以该模型通过了显著性检验。根据t统计量的计算公式计算得tb1=0.707，tb2

=1.259，tb3

=-2.719，当显著性水平为α=0.01时，t0.01/2（12-3-1）=3.5，tb1，tb2，tb3均通过检验。

对预测误差进行检验，通过计算，平均绝对百分比误差MAPE=4.05%，小于10%，属于高精度预测。因此可用求得的多元线性回归模型对公路货运量进行预测。

（2）二次指数平滑法。通过对α的多次试算，此处选取的平滑系数α为0.4，此时平均绝对百分比误差MAPE最小。经计算得：

因此趋势模型方程为：

对模型进行预测误差检验，通过计算，平均绝对百分比误差MAPE=6.82%，小于10%，属于高精度预测。

（3）GM（1，1）模型

第三步，检验X（1）是否具有准指数规律

因此可以确定模型为：

为了确认该模型是否合格，需对模型进行检验，通过计算，均方差比值C=0.168，根据表1可知均方差比值精度为一级（优）。小误差概率P=1，精度为一级（优）。平均绝对百分比误差MAPE=4.22%，小于10%，属于高精度预测。故该模型为合格的，可用来预测公路货运量。

（4）组合预测结果。根据2.2.2中的权重计算方法，计算得出多元线性回归、二次指数平滑法、GM（1，1）模型所占权重分别为0.49，0.22，0.29。多元线性回归模型考虑了其他因素的影响，能较好地反映货运量与经济的关系，其权重系数在三种预测方法中最高，说明其预测值更接近实际情况。组合预测模型公式为：

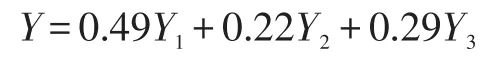
根据上述组合预测模型计算预测结果，预测结果见表3。

表3　预测结果 （单位：万t）

（5）误差指标结果。根据2.3中的公式计算出各预测方法及组合预测法的5种误差指标，计算结果见表4，从表4可以看出，组合预测结果中，MAE、MAPE、MSPE这三个误差指标值是最低的，SSE误差指标值仅次于GM（1，1）模型、MSE误差指标值仅次于多元线性回归模型，说明基于信息熵的组合预测模型对提高预测精度有一定的意义。

表4　误差指标计算结果

4　结语

本文采用基于熵权法的组合预测方法，综合利用了多元线性回归、二次指数平滑及灰色预测这三种单一模型所提供的信息，克服了单一预测模型在货运量预测中的局限性，达到了提高预测精度的目的。从实例分析中可以看出，采用基于信息熵的组合预测模型，各个误差指标都有了一定程度的改善，拟合结果优于单一模型的预测结果，说明采用此组合预测模型具有一定的合理性和优越性。

［1］陈实.货运量预测方法与应用研究［D］.武汉:武汉理工大学，2008.

［2］宋光平.铁路货运量预测方法研究［D］.北京:北京交通大学，2007.

［3］邓聚龙.灰色系统基本方法（第二版）［M］.武汉:华中科技大学出版社，2005.

［4］湖南统计局.湖南统计年鉴［M］.北京:中国统计出版社，2013.

Combination Forecasting of Highway Freight Volume Based on Entropy Weighting

Zhan Bin，Lv Lamei，Huang Xin
（School of Transportation，Wuhan University of Technology，Wuhan 430061，China）

In this paper，we established an entropy weighted combination forecasting model based on the multiple linear regression model，secondary exponential smoothing method and GM（1，1）model.Then through an empirical study，we proved that as compared with the individual models，the combination model had lower forecasting risks and system errors and higher forecasting accuracy.

highway freight volume；entropy weighting；combination forecasting

U492.313；F224

A

1005-152X（2016）06-0054-04

10.3969/j.issn.1005-152X.2016.06.013

2016-04-12

詹斌（1966-），男，湖北武汉人，武汉理工大学交通学院教授，主要研究方向：交通运输规划与管理；吕腊梅（1992-），女，湖北随州人，武汉理工大学交通学院硕士，主要研究方向：交通运输规划与管理；黄馨（1993-），女，湖南怀化人，现供职于海丰国际。