随机环境下的废旧家电产品逆向物流库存模型

刘志峰，赵　鹏，黄海鸿，沈丙涛

（合肥工业大学　机械与汽车工程学院，安徽　合肥　230009）

随机环境下的废旧家电产品逆向物流库存模型

刘志峰，赵鹏，黄海鸿，沈丙涛

（合肥工业大学机械与汽车工程学院，安徽合肥230009）

为降低废旧家电回收库存成本，优化回收过程库存控制策略及库存控制参数，结合当前的废旧家电回收流程，构建了包含收集点、回收中心和回收工厂的三级开环逆向供应链。根据废旧家电产品到达各收集点服从参数不同的泊松分布，提出收集点和回收中心的批量送货策略；以一个运作周期内的库存成本为控制目标，建立一种随机环境下的三级回收体系逆向物流库存模型。应用改进的遗传算法求解模型，得到了收集点与回收中心的最优送货量和送货时间，及其在一个运作周期内的平均回收费用。最后，通过算例验证了模型的可行性。并在此基础上，分析了废旧家电的平均到达率对库存控制策略的影响。

随机环境；回收体系；废旧家电；逆向物流；库存模型

1　引言

据统计，2014年以来我国每年各类废旧家电产品总量达到1亿台以上。这些废旧家电产品中不仅含有大量的可再利用零部件，还有一些危害环境的废弃物，如不妥善处理，不仅会污染环境，而且会浪费大量资源。废旧家电产品的回收再利用成为了人们关注的焦点，为实现家电回收而产生的物流技术即逆向物流，也越来越得到企业与研究院所的重视。逆向物流最早于1992年Stock提出，是一种产品退回、物料替代、物品再利用、废弃处理、再处理、维修与再制造等流程的物流活动［1］，其运作网络如图1所示。

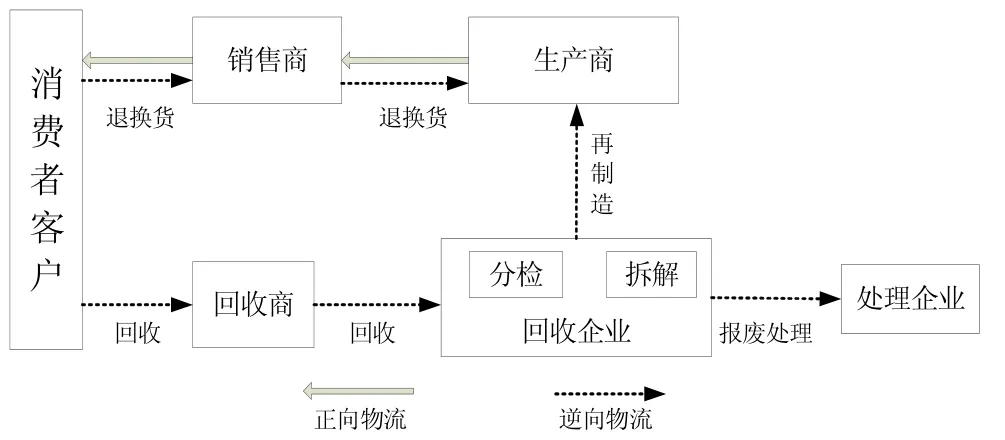
图1　逆向物流运作网络

库存控制是逆向物流研究的一个重要方向。国外学者较早开展了逆向物流库存管理的研究。Schrady［2］第一个提出了逆向物流库存模型，假设产品的需求率和回收率一定，且产品再次订货的费用不变的情况下，建立了一种维修库存的确定型模型，求得了最优的订购量和修复量。Tenuter［3］研究了制造、再制造混合生产的库存控制问题，Toktay［4］研究了再制造过程中需求率、生命周期等对产品库存影响的问题，Fleichmann［5］提出了退货回收的产品可以再销售的逆向物流库存模型，Dobos［6］对含回流产品的逆向物流库存进行了研究。同时，多个学者针对需求和回收都服从随机分布的逆向物流库存模型进行了研究［7-9］。近年来，国内学者也开始关注逆向物流库存管理的研究。在针对产品退货或维修的逆向物流库存方面，黄祖庆［10］研究了产品退货后可修复再售的销售商最优订货模型，探讨了退货率对销售商收益及订货策略的影响；陈铓［11］对回收品可维修的库存控制模型进行了研究，同时考虑了连续时变需求对模型的影响。针对产品回收的逆向物流库存研究方面，狄卫民［12］研究了回收中心和回收工厂的二级生产库存，得到了回收中心在一个周期的运输批次、每次运输量以及相应的库存费用；苟清龙［13］建立了“单中央处理中心—多本地收集点”的两级逆向供应链的联合库存模型；曹柬等［14］研究了随机回收和库存有限的情况下逆向供应链成员企业之间的决策问题。

纵观国内外关于逆向物流库存管理的研究，早期主要针对产品退货与维修处理建立库存模型，近年来则重点研究了面向再制造的库存模型；但这些研究大多仅针对逆向物流中某一级具体库存或者二级库存，研究回收逆向物流多级库存的较少。与其它废旧产品相比，废旧家电产品具有分散性和随机性特点，结合废旧家电产品的回收现状可知，废旧家电回收主要依靠个体商贩、零售商将回收的废旧家电运往回收中心和拆解处理企业。废旧家电产品的回收逆向物流网络是由“消费者—回收点—回收中心—拆解处理商”组成的一个开环逆向供应链，因此针对废旧家电产品逆向物流网络的库存控制研究很有必要。本文构建了由若干个收集点、若干个回收中心和一个回收工厂组成的回收系统。各收集点负责将回收的废旧家电运送到所属区域的回收中心，各回收中心负责将检测分拣处理后的废旧家电送往回收工厂，回收工厂负责废旧家电产品的拆卸与回收。考虑到废品到达时间、到达数量等多个与库存相关的参数均是随机的，本文提出了随机环境下收集点和回收中心的送货策略，构建了一种三级回收的逆向物流库存控制模型，并探讨了废旧家电的平均到达率对库存控制策略的影响。

2　问题描述

在三级回收网络中，由于废旧家电产品到达各收集点的时间和数量是不确定的，因此其中各级库存都存在着随机性，相应的成本管理费用也是不确定的。为了解决废旧家电产品回收时间和数量不确定性对回收过程的影响，对收集点和回收中心均采用批量运送策略，寻找最优的决策量使得整个回收网络的平均运作成本最小。为便于建立模型，进行以下假设：

（1）整个回收网络以回收工厂为核心，回收工厂协调控制回收中心的库存活动，回收工厂采用中心化库存控制策略。

（2）各收集点的回收方式根据其所处的生活环境采用不同的回收方式（如以旧换新、商返和个体回收等），废旧家电到达过程为泊松过程，不同收集点的平均到达率为λi（i=1，2，...，n）且各收集点废品到达过程相互独立。

（3）收集点采用数量驱动库存策略，设定一个可送货水平Q，当收集点库存量达到Q时，收集点即向回收中心运送废旧家电，废旧家电短时间内即可到达，不考虑运输提前期对系统优化的影响。

（4）回收中心采用联合数量驱动库存策略，回收工厂实时监控各回收中心库存，当所有回收中心的库存量之和达到库存水平S时，回收中心向回收工厂送货，同理不考虑运输提前期对系统优化的影响。

（5）回收工厂开启生产，受各收集点收集水平的影响，回收中心相邻两次运送时间间隔为研究的一个运作周期，运作周期由所有回收中心的库存量之和达到库存水平S所需时间决定，由回收工厂实时监控，下达运送指令，此时各回收中心完成清库运送。

（6）回收工厂的处理能力大于回收中心的回收能力，因此回收工厂存在缺货，若以最大处理能力处理，必须采用间隙生产。

（7）回收过程考虑7种类型的成本：收集点的运送成本、收集点的存储成本、回收中心的运送成本、回收中心的存储成本、回收工厂的处理成本、回收工厂的存储成本、回收工厂的缺货成本。

（8）各收集点的库存容量大于Q，回收中心的库存容量大于S，回收工厂采用租赁仓库的方式存储废品。

根据以上假设，收集点、回收中心和回收工厂的库存变动如图2所示。

图2　回收库存示意图

3　模型建立

3.1符号说明

P为回收工厂的最大处理能力；

Tm为回收中心最长送货时间；

Ti为收集点送货的时间间隔，i=1，2，…，n；

C1为收集点单位时间单个库存存储费用；

C2为收集点运送一次的运送费用；

C3为回收中心单位时间单个库存存储费用；

C4为回收中心运送单位产品的运送费用；

C5为回收工厂单位时间单个库存存储费用；

C6为回收工厂单位产品一次的处理费用；

C7为回收工厂单位产品的缺货成本费用；

C8为回收中心向回收工厂组织一次运输的启动成本；

T为一个运作周期；

T0为回收工厂的间隙期；

Q为收集点每次送货的废品量；

Qr为收集点的回收能力；

S为回收中心的送货批量；

n为收集点的个数；

m为回收中心的个数；

α为采用个体回收方式的收集点个数；

β为采用以旧换新方式的收集点个数；

γ为采用商返方式的收集点个数；

λi为i收集点废品到达的平均到达率，i=1，2，…，n；

F（Q，T）为回收体系单位时间与回收库存相关的平均回收费用。

3.2建立模型

根据上述描述可知，废旧家电产品到达收集点的过程为平均到达率为λi的泊松过程，对于任一收集点i的库存量累积到Q的平均时间间隔Ti为：

则所有回收中心库存量之和达到S所需时间满足以下条件：

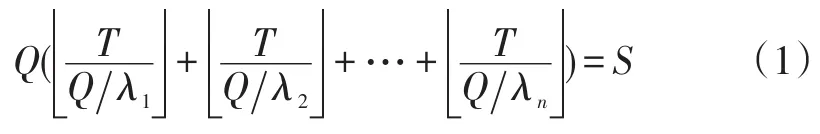
对于任意收集点i，在一个运作周期T内向回收中心送货次数Ni为：

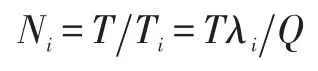
对Ni取整为即一个T时间内，所有收集点向回收中心运送了次废品，Q和S的关系可用下式表示：

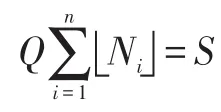
收集点i在Ti时间内收集的废品存储费用为：

则在不足一个Ti时间内收集点i收集的废品存储费用为：

所有收集点在一个运作周期T内收集的废品存储费用为：

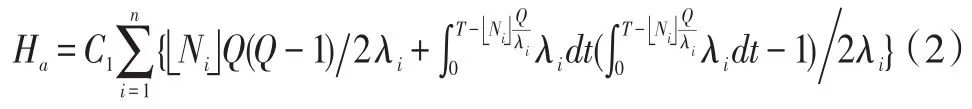
因此回收中心在T时间内的废品存储费用为：

回收工厂在一个T时间内处理的废品存储费用为：

根据假设条件6可知，回收工厂实际处理量小于回收工厂的最大处理量，因此回收工厂必须间歇处理，间歇期为：

间歇期内回收工厂的缺货成本费用为：

一个T时间内所有收集点送货的运输成本Ts为：

根据假设条件5可知，各回收中心在每一个运输周期内需对回收工厂进行一次送货。回收中心的运输成本与运送量、回收中心个数有关，则回收中心运送到回收工厂的运输成本Th为：

回收工厂在一个运作周期内处理费用为：

各收集点采用三种不同的收集方式回收废旧家电，因此收集点个数存在以下关系：

为了求得各收集点、回收中心的最佳送货量和送货时间，将上述讨论的各项成本相加，得到回收网络在一个运作周期T内的平均回收费用：

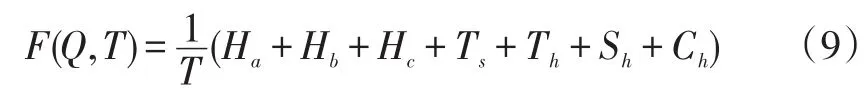
因此，研究的问题将转变为函数F（）的优化问题：

其中：式（10）保证各收集点运送量不得超过各自的回收能力，式（11）保证回收中心的送货时间范围，式（12）保证回收工厂间歇时生产，式（13）保证收集点运送量与回收中心运送量、运送时间的关系。上述式中n，m，λi，C1，C2，C3，C4，C5，C6，C7，P，Qr，Tm均为定值。

4　模型求解

模型诠释了随机环境下三级回收体系逆向物流的库存控制情况，单纯的运输或者存储问题很难对其进行求解。遗传算法不需考虑问题的具体领域，具有大规模搜索能力和鲁棒性，因此引入遗传算法对模型进行求解，但考虑到遗传算法本身可能出现的早熟现象，陷入局部最优循环，本文在遗传算法的基础上，引入自适应机制和评价机制，建立更加适合解决模型问题的改进遗传算法进行模型求解。具体算法步骤如下：

（1）编码。采用一维二进制对决策变量Q和T进行编码，编码方案采用串联编码，整个染色体分成两段，如图3所示。染色体表示收集点的送货方案和回收中心的送货时间，假设收集点的库存容量不超过1 000，回收中心送货时间不超过7d，收集点的送货量由10个基因表示，回收中心送货时间由3个基因表示。例如，图3中的编码表示收集点的送货量为90台，回收中心送货时间为3d。

图3　决策变量Q和T编码

（2）适应度函数。得到的决策变量Q和T不一定满足式（12）和式（13）的约束条件。因此，构建包含惩罚因子和目标函数的适应度函数，对于不满足约束条件的个体i，给其惩罚因子YD（D是一个很大的正数，Y=1），符合条件的个体Y=0，则对于某个体的目标函数值为Fi，其适应度fi为:

（3）选择算子。为了使适应度高的优良个体尽可能的出现在下一代，采用轮盘赌选择法。即个体的适应度越大，该个体保留下来的几率就越大，适应度为fi的个体i的选择函数为：

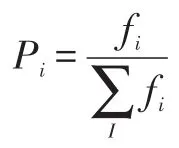
（4）交叉算子及其自适应机制。采用两点交叉算子，按自适应交叉率Pc进行交叉操作，随机选择交叉点，将该点两个个体部分进行相互交换，从而产生两个新的个体。

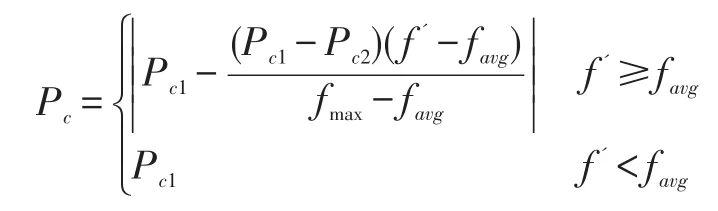
其中fmax为群体中个体最大的适应度值，favg为群体的平均适应度值，f’为两个个体中较大的适应度值，Pc1、Pc2为初始设定值。

（5）变异算子及其自适应机制。为了保证种群的多样性，采用基本位变异，按变异率Pm随机选取某一个基因进行变异。考虑到本模型的实际情况，引入如下自适应机制，自动调整Pm的取值。

其中f为个体的适应度值，Pm1、Pm2为初始设定值。

（6）评价机制。交叉产生的两个新个体，与其父代个体进行适应度计算，若两个新个体适应度最高，则选择新个体进入下一代种群，否则采用轮盘赌选择法，从父代和子代四个个体中选择两个个体进入下一代种群。

变异产生的新个体，与变异前个体进行适应度计算，若新个体适应度高，则接受新个体替代变异前个体，若新个体适应度低于变异前个体，则采用轮盘赌选择法，从中选择一个个体进入种群。

（7）终止条件。给定一个足够大的终止迭代次数，迭代达到稳定后输出最优解。

5　案例分析

以安徽省芜湖一废旧家电回收处理工厂在区域内设置了若干个收集点、若干个回收中心来回收处理废旧家电。各收集点将回收的废旧家电统一回收到回收中心，各回收中心将回收的废旧家电累积到一定量时运送到回收处理工厂进行拆解。由于相关的商业数据涉及机密，本文结合实际调研设计了一组数据。其中n=30，m=3，α=14，β=10，γ=6，C1=5，C2=1 000，C3=3，C4=3，C5=15，C6=20，C7=40，C8=2 000，P=1 500，Qr=10 000，Tm= 30。30个收集点分三组，每组10个，分别隶属于A、B、C三个回收中心，各收集点只向其所属回收中心送货，其废旧家电平均到达率见表1。

表1　回收中心所属收集点的废旧家电平均达到率（单位：台）

采用遗传算法求解，初始条件为：种群规模Size= 20，最大迭代次数max_gen=200，交叉概率Pc1=0.9，Pc2= 0.3，变异概率Pm1=0.1，Pm2=0.001。改变初始解，进行多次计算，适应度和最优解图形均收敛，取平均值后，优化结果见表2。

表2　控制参数

由表2可知，一个运作周期为3d。根据批量送货策略，当各收集点的废旧家电库存水平达到56台时，各收集点向所属回收中心送货；回收中心在一个周期内向回收工厂运送3 472台废旧家电，其中A回收中心送货1 232台，B回收中心送货1 008台，C回收中心送货1 232台；在一个周期内，整个回收系统的平均回收费用为90 732元。同时，回收工厂需要租赁相应的仓储空间；回收工厂若以最大处理能力回收废旧家电，处理时间为2.32d，其回收处理量达到产能的78%。

与已有文献及研究成果对比［12-13］，本模型加入了多个收集点和多个回收中心，考虑了回收过程废旧家电回收时间和数量的不确定性，给出了各收集点相互独立的废品到达分布，更加符合废旧家电回收实际情况。此外，模型中考虑了回收工厂的缺货成本，确定的最佳经济送货量可使废旧家电产品得到及时处理，避免回收中心的库存大量积压。

由于构建的库存模型考虑了废旧家电产品回收数量和时间的随机性，因此平均到达率对收集点和回收中心送货量、平均回收费用均有重要影响。保持初始条件不变，假设所有收集点的平均到达率一致，则在一个运作期T内，平均回收费用F最优的前提下，平均到达率对收集点和回收中心送货量的影响结果如图4与图5所示。

图4　收集点最优送货量的变化趋势

图5　回收中心最优送货量的变化趋势

由图4、图5可知，收集点和回收中心的最优送货量随着平均到达率的增加先递增后递减；当平均到达率在一定范围内增加时，缺货成本减少的速度大于其它成本的增加速度，因此收集点和回收中心的最优送货量呈递增状态；而当平均到达率增加到某一程度后，缺货成本减少的速度小于其它成本的增加速度，收集点和回收中心的最优送货量则呈递减状态。由此可知，废旧家电产品回收过程中的随机性对库存控制策略有重要影响；可以通过求解本文提出的模型，得出收集点和回收中心的经济送货批量。

6　结论

针对构建的废旧家电产品三级回收网络体系，提出了收集点和回收中心在随机环境下的送货策略；假设废旧家电产品回收数量服从泊松分布，建立以逆向物流成本为优化目标的库存控制模型。通过对模型的求解，可得到一个运作周期内收集点、回收中心的最佳送货量和送货时间。通过案例分析验证了模型的可行性，进而分析了平均到达率为库存控制策略的影响。此外，模型的建立可为各级回收单位的库存容量设计以及回收工厂的生产管理决策提供理论依据。未来的研究可围绕多周期各级库存控制以及多目标优化进一步深化开展。

［1］Stock J R.Reverse Logistics.Council of Logistics Management［R］. Oak Brook，IL，1992.

［2］Schardy D A.A deterministic inventory model for reparable items［J］.Naval Research Logistics Quarterly，1967，14（3）:391-398.

［3］Teunter R H.Economic ordering quantities for remanufacturable item inventory system［Z］.University of Magdeburg，Germany，1998.

［4］Toktay L B，Wein M，Zenios S A.Inventory management of remanufacturable products［J］.Management SC，2000，46（11）:1412-1 426.

［5］Fleischman M，Kuik R，Dekker R.Controlling inventories with stochastic item returns:a basic mode1［J］.European Journal of Operational Research，2002，138（1）:63-75.

［6］Dobos I.Optimal Production-inventory strategies for a HMMS-type reverse logistics system［J］.International Journal of Production Economics，2003，（81-82）:351-360.

［7］Fleischman M，Kuik R.On optimal inventory control with independent stochastic item returns［J］.European Journal of Operational Research，2003，151（1）:25-37.

［8］Mahadeva B，David P F，Fleischman M.Periodic review，Pushinventory policies for remanufacturing［J］.European Journal of Operational Research，2003，16（3）:536-551.

［9］Teuntera R，Kaparisa K，Tang O.Multi-product economic lot scheduling problem with separate production lines for manufacturing and remanufacturing［J］.European Journal of Operational Research，2008，16（3）:1 241-1 253.

［10］黄祖庆，达庆利，王冬冬.逆向物流具有时滞的一个EOQ扩展订货模型［J］.物流技术，2004，（5）:82-84.

［11］陈铓，符桌.连续时变需求与回收率相关的维修备件库存优化［J］.计算机集成制造系统，2012，18（5）:1 087-1 092.

［12］狄卫民，王梅杰.回收物流系统生产库存优化模型［J］.计算机集成制造系统，2010，16（7）:1 539-1 544.

［13］苟清龙.逆向供应链中的若干联合库存策略［D］.合肥:中国科学技术大学，2007.

［14］曹柬，陈雅，张雪梅.基于随机回收和有限库存的逆向供应链决策分析［J］.中国机械工程，2012，25（10）:1 387-1 394.

Waste Electrical Appliance Reverse Logistics and Inventory Model under Stochastic Environment

Liu Zhifeng，Zhao Peng，Huang Haihong，Shen Bingtao
（School of Mechanical&Automobile Engineering，Hefei University of Technology，Hefei 230009，China）

In this paper，in order to lower the expenses in the recycling and inventory of waste electrical appliances，and optimize the strategy and parameter of inventory control in the recycling process，and in view of the current waste electrical appliance recycling process，we established the three-echelon open-looped reverse supply chain comprising the collection points，recycling center and recycling factory. Then we proposed the batched cargo delivery strategy for the collection points and recycling center and established the reverse logistics and inventory model for the three-echelon recycling system under the stochastic environment.Next，using the improved genetic algorithm，we derived the optimal delivery volume and time for the collection points and recycling center，as well as the average recycling cost in one operational cycle.At the end，we verified the feasibility of the model，on the basis of which we analyzed the influence of the average arrival ratio of the waste electrical appliances on the inventory control strategy.

stochastic environment；recycling system；waste electrical appliance；reverse logistics；inventory model

F426.6；F253

A

1005-152X（2016）06-0044-06

10.3969/j.issn.1005-152X.2016.06.011

2016-05-11

国家863计划资助项目“退役家电产品逆向物流关键技术研究与示范”（2013AA040205）

刘志峰（1963-），男，陕西宝鸡人，教授，博士生导师，主要研究方向：绿色设计、退役家电逆向物流、废旧产品再资源化方法与装备等；赵鹏（1992-），男，安徽亳州人，硕士，主要研究方向：逆向物流控制；黄海鸿（1980-），男，安徽安庆人，教授，博士生导师，主要研究方向：绿色制造与再制造、无损检测等；沈丙涛（1989-），男，安徽霍山人，硕士，主要研究方向：逆向物流库存控制。