冷链物流优化模型构建

林道荣，张 顺，蔡成芳

（1.南通大学杏林学院，江苏 南通 226007；2.南通大学 理学院，江苏 南通 226019）

冷链物流优化模型构建

林道荣1，2，张 顺2，蔡成芳1

（1.南通大学杏林学院，江苏 南通 226007；2.南通大学 理学院，江苏 南通 226019）

主要从分析冷链物流所运输的冷链产品特点出发，首先考虑冷藏（冻）车装载冷链产品货箱或冷藏（冻）箱的问题，根据目的地的实际需求，考虑到棱“相似”、面“相似”、体“相似”或棱“相等”、面“相等”、体“相等”情况，利用等价替换，构建了其他装载方案模型；其次是冷藏（冻）车的派发问题，并把目的地分为终点性目的地和中转性目的地来进行分析，建立了冷链配送优化模型；最后，通过对江苏中洋集团的实际调研，验证了所建模型的合理性与正确性。

冷链物流；配送模型；启发式算法；冷藏（冻）车

1 引言

冷链物流（Cold Chain Logistics）是随着科学技术的进步和制冷技术的发展而建立起来的，是指冷藏冷冻类食品在生产、储藏、运输、销售等消费前的各个环节中始终处于规定的低温环境下，以保证食品质量，减少食品损耗的一项系统工程，也称为低温物流［1］。冷链物流问题，本身是一个复杂的决策问题，对于该问题，要考虑的因素较多，如冷链产品货箱的各种型号、冷藏（冻）箱的各种型号、冷藏（冻）车的各种型号，根据目的地的需求量，需要多少个产品货箱，需要多少辆冷藏（冻）车，冷藏（冻）车（箱）装载产品货箱时，采取什么样的装载方式，装载多少个，冷藏（冻）车的运输路线，以及运输途中的各种成本等。从数学上来看，这是一个组合优化问题，属于一个NP-hard问题［2］，NP-hard问题要在理论上求得最优解是非常困难的.

冷链物流问题就是要解决在保证需求的情况下，考虑各种运输因素，使得成本最少。对于目标成本，有固定成本和不固定成本，固定成本包括装载成本、人工成本、货缺成本等。不固定成本有货损成本、产品的冷冻成本、过路费等各种运输成本。通过实际考察物流的操作流程，发现绝大多数物流问题都是分为两个阶段，一是冷藏（冻）车（箱）装载产品货箱，是货箱装载的组合问题。由于冷链产品的特殊性以及冷藏（冻）车的性能不同，装载可分为两种类型，若冷藏（冻）车的厢底保温效果较好，可直接把产品货箱放在车内装载，即冷藏（冻）车装载产品货箱；若冷藏（冻）车的厢底保温效果较差，应首先把产品货箱放置在冷藏（冻）箱内，然后再放在车内装载，即冷藏（冻）车装载冷藏（冻）箱。另一个是冷藏（冻）车发往各个目的地的运输问题，根据运输成本最小，选择合适的装载方案，是整数线性规划问题。

2 模型的建立

2.1 构建最优装载方案模型及求解算法

对于冷藏（冻）车（箱）如何装载产品货箱，需要研究其装载方式。理论上，可采用枚举装载，得到可装载方式，但是枚举法的缺点是计算量比较大。注意到装载工人们实际装载时采用的是层放法，因此应当采用层放法来确定可装载方式。货箱的装载方式有可装载方式、最优装载方式、有效装载方式。可装载方式有很多，可通过枚举法得到，装载后还有剩余空间，但是工作量较大。最优装载方式只有一种，是利用率最大的装载方式，可充分利用空间，剩余空间较少，不能再装载其他种类的货箱。针对最优装载方式，改变一种货箱的数量，再装载其他类型的货箱，即部分货箱指定的装载方式，也是可装载方式。但是根据实际需求，需要的是有效装载方式，即根据具体的需求，确定实际的装载，但利用率不高。实际装载中，采取有效的装载方式，考虑货箱的顺带，从而提高利用率。

在货箱装载中，以冷藏（冻）箱里侧左下方的顶点为原点，箱底在xoy面上，箱门在yoz面上，建立三维直角坐标系。规定在三维长方体中，在x轴上截取一定厚度的用平行于yoz面的平面进行切割，在y轴上取一定厚度的用平行于面zox的平面进行切割，在z轴上取一定厚度的用平行于面xoy的平面进行切割［3］。对于某种型号的冷藏（冻）箱，可用表示体积，其中X表示x轴方向的长度，Y表示y轴方向的长度，Z表示z轴方向的长度。如果整个最优装载过程分为k步，则冷藏（冻）箱空间可分为k个装载空间其中表示第i步的装载空间，分别表示长、宽、高。可用表示在第i步时冷藏（冻）箱剩余的k-i个装载空间所成的立体空间，称为第i+1步的可装载空间。如果有n种产品货箱，用 j#表示第 j种型号箱子（j=1，2，...，n），这n种不同规格的箱子的重量为g1，g2，...，gn，规定冷藏（冻）箱的最大载重量为G。用表示第 j种型号的箱子的体积，其中分别表示长、宽、高。可用lij表示第i步装入第 j种型号箱子的个数，为第i步装入各种型号货箱的向量。可用表示第i步装载后n种型号箱子摆放货箱的总数量，其中且由以上可知，L=Lk，并且有

由于货箱本身具有不能分割或挤压等物理性质，在装载过程中，应考虑货箱本身的抗压能力，以及所能承受的最大压力。对于排在上层的过重的货箱可通过整层置换的方式调整到较下面的层。通过解决动态规划问题，可求得理论上的最优解，但由于理论并不一定具有可操作性，理论上的最优解也不能体现装载过程。

通过对问题的一系列分析，可以考虑建立多步决策局部优化模型如下：对于冷藏（冻）箱的装载过程可分为k步。第1步是从可装载空间中确定层第 2步是从可装载空间中确定层第i步是从可装载空间中确定层···，按一种坐标面层放法后使该层的利用率达到最大：

相应的约束条件为：

2.2 构建其它可装载方案模型及求解算法

最优装载是采用层放法，对于其他可装载方式，则不局限于层放法。若整个装载过程分为M步，如果有n种冷链产品货箱，数量依次为l1，l2，...，ln，每个货箱的体积为vj（j=1，2，...，n），重量为gj（j=1，2，...，n），整个冷藏（冻）箱的装载空间为V。lij表示第i步装入第 j种型号箱子的个数，Li为第i步装载后n种型号箱子摆放货箱的总数量。对于最优装载方式进行调节，若根据需求，前 s种货箱数量一定，分别为其中首先利用棱判别矩阵找出空间利用率最差的货箱若冷藏（冻）箱只装载得到空间利用率为ηq，而根据上述最优装载，得到的最大利用率为可建立如下只有约束条件没有目标函数的其他可装载方式模型：

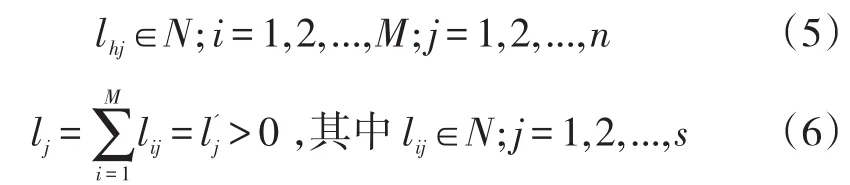
对于其他可装载模型的求解也可以设计一定的求解算法。

Step2：按货箱体积大小由大到小装载，若各种货箱的装载量为其中先减少i1个体积最大的货箱对于剩余空间进行装载，各种货箱装载后的装载量为

Step3：再减少i2个体积次大的货箱对于剩余空间进行装载，若各种货箱装载后的装载量为

...

Stepη（η=4，5，...，n-2）:再减少iη个体积次大的货箱对于剩余空间进行装载，若各种货箱装载后的装载量为

...

2.3 构建冷链物流优化模型及求解算法

对于冷链产品的运输问题，首先可看作常规的运输问题，即从起点到终点运输各种产品，满足各个目的地的需求。问题中涉及许多的决策变量，比如冷藏（冻）车指派多少辆，如何运输，每辆车的装载方式，运输路线的网络布局复杂性导致选择哪条运输路线，以及综合考虑运输的各种成本问题等。若选择较好的决策变量，可构建模型来解决。综合各个目的地的需求量，应先考虑距离较远的终点性目的地的需求量，以及一些较大客户的需求量，再考虑距离较近的中转性目的地的需求量，以及一些小客户的需求量。并根据目的地的具体需求，确定具体的运输路线；可根据冷藏（冻）车装载产品货箱或冷藏（冻）箱的可装载方案，结合各个目的地对于冷链产品的需求情况，选择冷藏（冻）车；最后顾及到达终点性目的地的冷藏（冻）车可以为中转性目的地顺带货箱，考虑各种运输成本，得到满意的冷链运输方案。

对于冷藏（冻）车的装载问题，可用Q表示类型量，Mq表示第q型冷藏车拥有量的向量，则 M→=（M1，M2，...，MQ）。对于货箱或冷藏（冻）箱，可用L表示类型量，l为箱的类型序号，表示第l型货箱或冷藏（冻）箱，l=1，2，...，L。对于冷藏（冻）车的不同装载方式，用nq表示第q型冷藏（冻）车充分装载货箱或冷藏（冻）箱的方案数。用表示对于第q型冷藏（冻）车采用第 j种装载方式装载的第l型货箱或冷藏（冻）箱的数量，两列时保持两侧对称。Cq表示第q型车装载箱子的数量矩阵，q=1，2，...，Q，其中用gl表示第l型货箱或冷藏（冻）箱的总重量。

对于运输的目的地，用Z表示目的地的总数，z表示目的地序号，为第z个目的地，其中表示各种型号货箱或冷藏（冻）的总需求量或待运量的向量，其中表示第z个目的地的需求量向量其中Plz表示第 z个目的地对第l型货箱或冷藏（冻）箱的需求量，l=1，2，...，L；z=1，2，...，Z。P为需求量矩阵，其中P=表示对第z个目的地的需求量在选用第 j种货箱或冷藏（冻）箱装载方案的第q型冷藏（冻）车的数量，yqz表示第z个目的地装载货箱或冷藏（冻）箱所需的第q型冷藏（冻）车的数量，其中可知q=1，2，...，Q；z=1，2，...，Z。yq表示所需第q型冷藏（冻）车的数量，其中

由于车辆运输成本计算较为复杂，可以这样简化：冷藏（冻）车的使用量行驶里程运价距离系数运输过程中的过路费表示q型冷藏（冻）车从起点O到目的地Az的第s条运输路线的过路费；冷冻费表示q型冷藏（冻）车从起点O到目的地Az的第s条运输路线的冷冻费。这样辆第q型冷藏（冻）车行驶里程的运输成本表示为在此基础上对运输路线累加，再对车型累加即得总成本。

对于决策变量，如果从生鲜产品供应地起点到每一个需求目的地只有单一运输路线，采用表示对第z个目的地的需求量，冷藏（冻）车选用第j种装载方式装载货箱或冷藏（冻）箱所需第q型冷藏（冻）车的数量，其中，q=1，2，...，Q；z=1，2，...，Z；j=1，2，...，nq。如果从生鲜产品供应起点到一些需求目的地有多种运输路线，这样的目的地记为A1，A2，...，Az0，这里1≤z≤Z0。对于目的地假设有Kz条路线，采用表示对第z个目的地的部分需求量，在以起点O到目的地Az的第s条路线上，冷藏（冻）车选用第 j种装载方式装载货箱或冷藏（冻）箱所需第q型冷藏（冻）车的数量，其中并用表示从起点O到目的地Az的第s条运输路线所派的第 q型冷藏（冻）车的数量，显然其中z=1，2，...，Z；s=1，2，...，Kz；q=1，2，...，Q。

对于目标函数，利用hzs表示从起点O到目的地Az的第 s条运输路线的距离，其中，s=1，2，...，Kz；z=1，2，...，Z，用Kq表示第q型冷藏（冻）车的距离运价系数，用mzs表示q型冷藏（冻）车从起点O到目的地Az的第s条运输路线的过路费，用表示q型冷藏（冻）车从起点O到目的地Az的第s条运输路线的冷冻费，那么从起点O到目的地Az的运输里程成本为：

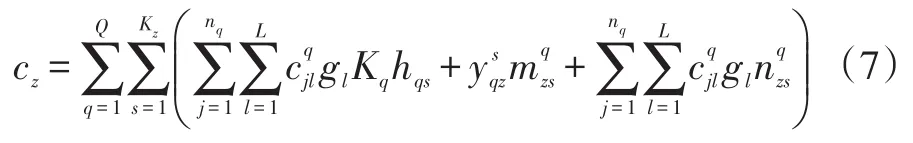
由此可得起点O到所有目的地的运输里程总成本为：

对于约束条件，把目的地分为两类，一类是终点性目的地，记为另一类是中转性目的地显然1＜u，v＜Z，且u+v=Z。

终点性目的地约束：用zt表示终点目的地的Bt目的地序号，则：

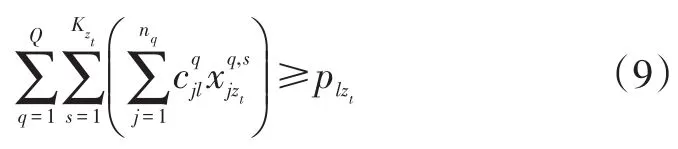
其中l=1，2，...，L；t=1，2，...，u；1≤zt≤Z。

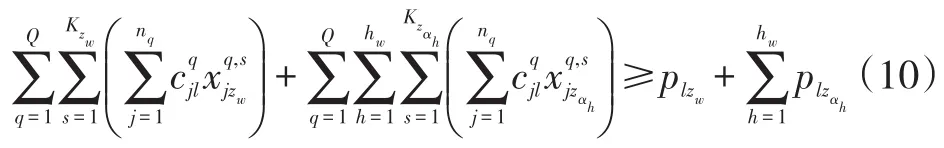
其中l=1，2，...，L；w=1，2，...，v。

对于冷藏（冻）车的变量关系约束：

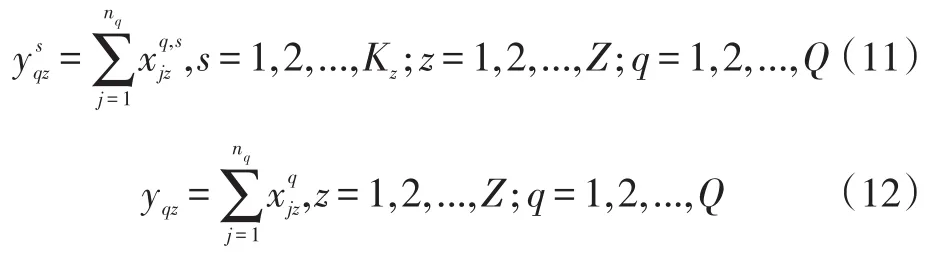
对于冷藏（冻）车变量数值约束：

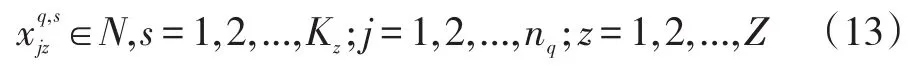
冷藏（冻）车与货箱或冷藏（冻）箱的使用量约束限制：

综上可得到一般优化模型形式，即以式（8）表示的目标函数为最小，式（9）—式（14）为约束的整数线性规划模型。

对于冷藏（冻）车的运输问题，首先应对车辆装载货箱或冷藏（冻）箱问题进行研究优化，列出各种可装载方案。然后结合考虑运输目的地的距离以及各种目的地的需求量，列出运输途中各种成本、运价系数、各种费用。对模型进行优化，以达到成本费用最低的目标［4］。根据建立的冷链配送优化模型，可设计一个启发式算法来解决问题。设计算法如下（为使算法简化，算法中冷藏（冻）车简称冷藏车，货箱或冷藏（冻）箱简称冷藏箱）：

Step1：冷藏车规格（长、宽、高、载重量）及拥有量，冷藏车型号数，冷藏箱规格（长、宽、高、载重量），冷藏箱型号数，目的地冷藏箱各型号需求量，目的地数目，起点到目的地的运输路线数目，起点到目的地各运输路线的距离，冷藏车单位里程运价系数，目的地序号，终点性目的地集合与序号，中转性目的地与序号等数据输入。

Step2：确定终点性目的地的各种运输方案

（1）针对此目的地的需求量，确定冷藏车车型及冷藏车装载冷藏箱的有效装载方案，并对一层的各有效装载方案按最优、次优...最差进行优劣排序。

（2）按一层的最优装载方案选择第一种型号的若干冷藏车车辆装载冷藏箱，直到用这种冷藏车正好装完结束；否则，剩余冷藏箱一辆冷藏车装完转（3），剩余冷藏箱不能装满一辆冷藏车转（4）。记录所用第一种型号的冷藏车的数量与装载情况。

（3）按一层的非最优装载方案选择第一种型号的若干冷藏车装载冷藏箱，直到用这种冷藏车正好装完；否则，剩余的冷藏箱不能装满一辆冷藏车，转（4）。记录并累加所用第一种型号的冷藏车的数量与装载情况。

（4）调整：减少一辆装满冷藏箱的第一种型号的冷藏车，其所装载冷藏箱连同之前剩余冷藏箱选择第二种型号的冷藏车。如果用一辆第二种型号的冷藏车基本能装载完冷藏箱（冷藏车上允许有空车位，但很少），结束；否则，再减少一辆装载冷藏箱的冷藏车，两辆冷藏车所装载的冷藏箱连同之前剩余冷藏箱选择第二种型号冷藏车。如果用两辆第二种型号的冷藏车基本能装载完冷藏箱（冷藏车上允许有空车位，但很少），结束；否则继续调整。记录并累计所用各种型号冷藏车的数量与装载方式。

Step3：确定中转性目的地的运输方案

（1）同Step2（1）。

（2）同Step2（2）。

（3）同Step2（3）。

（4）对剩余不能装满一辆冷藏车的冷藏箱向经过此中转性目的地的其它目的地的冷藏车进行添加装载，如果能添加装载完剩余冷藏箱，结束；否则转（5）。记录冷藏车型号、数量与装载方式。

（5）调整：减少一辆装满冷藏箱的第一种型号的冷藏车，其所装载冷藏箱连同之前剩余冷藏箱选择第二种型号的冷藏车。先考虑向经过此中转性目的地的其它目的地的冷藏车进行添加装载，如果用一辆第二种型号的冷藏车基本能装载完冷藏箱，结束；否则，继续调整（对经过此目的地的第一种冷藏车可以减少地调整）。

Step4：冷藏车运输路线确定与成本计算

（1）确定直达目的地的冷藏车型号、数量及运输路线距离，计算成本。

（2）确定非直达目的地的冷藏车型号、数量，停留地点与卸载冷藏箱型号、数量及运输路线距离，计算成本，并累加成本。

Step5：记录可行解与总成本。

Step6：可行解改进最优。

（1）多运输路线目的地车辆调整，运输路线距离长的线路减少运价系数高的并增加运价系数低的冷藏车；运输路线距离短的线路减少运价系数低的并且增加运价系数高的冷藏车，计算总成本，如减少继续调整，否则转（2）。

（2）离起点远的目的地冷藏车尽可能选用运价系数低的冷藏车，离起点近的目的地冷藏车尽可能选用运价系数高的冷藏车。计算总成本，如成本比以前减少，继续调整；否则停止调整，以调整前的可行解作为较优的解，结束。

3 实例分析

江苏中洋集团的冷链产品主要为海洋产品、禽肉产品以及乳制品，2015年7月的供应量分别为100.34t、113.02t、39.02t，其供应基地位于海安县、启东市、淮安市等地。冷链产品的运输车辆的规格、运价、冷链物流货物的规格分别见表1-表5，其中型号I、II和III主要是长途运输冷藏（冻）箱，型号IV主要是短途在县区内运输各种冷链产品货箱。

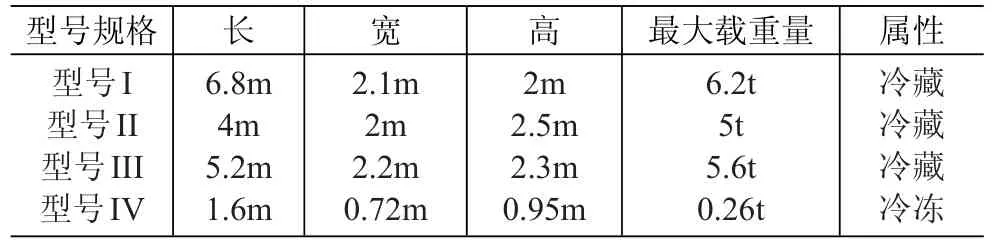
表1 冷藏（冻）车辆的规格

表2 冷藏（冻）车辆的性价比（每吨元/km）

表3 冷藏（冻）车辆的冷藏费基价（每吨元/km）

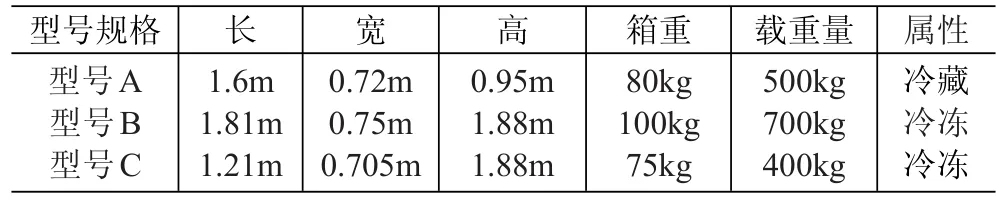
表4 冷藏（冻）箱的规格

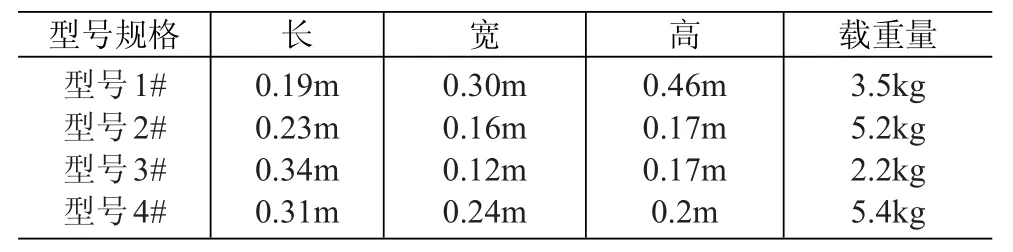
表5 产品货箱的规格

根据上述运输车辆和冷藏（冻）箱的规格，由于前三种运输车辆的宽度都满足可以同时并排放两个型号冷藏（冻）箱，列出三种运输车辆冷藏（冻）箱可装载方案，分别见表6-表8。

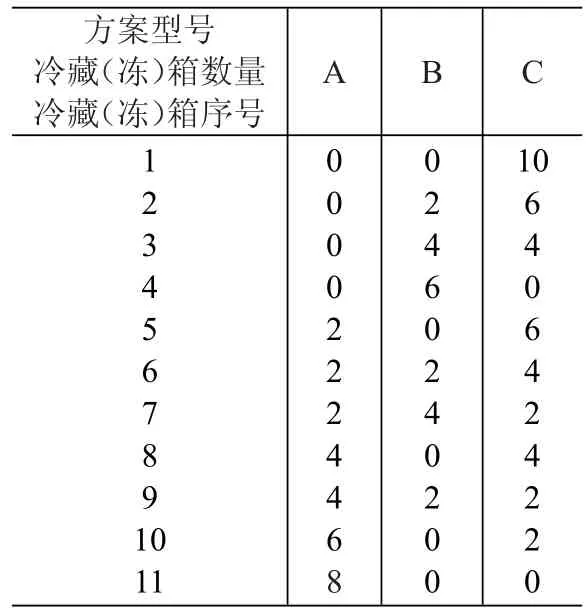
表6 型号I冷藏车辆装载各冷藏（冻）箱方案（单位：个）

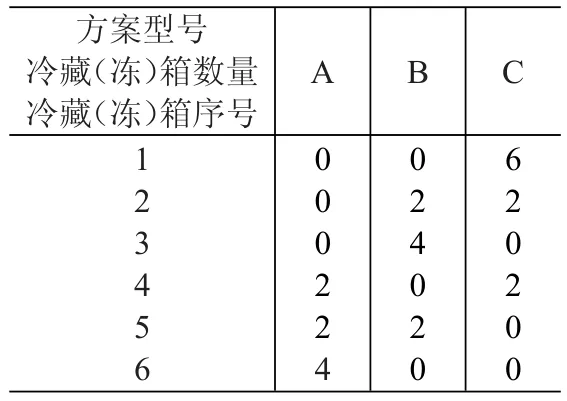
表7 型号II冷藏车辆装载各冷藏（冻）箱方案（单位：个）

表8 型号III冷藏车辆装载各冷藏（冻）箱方案（单位：个）

该集团冷链加工产品的需求企业主要有南通龙洋水产有限公司（b）、上海光明食品集团（c）、上海小南国餐饮集团（d）、南京鼎尚海鲜酒店有限公司（e）等。各企业2015年7月份需求量情况见表9。

表9 各企业7月份需求量情况（单位：t）

中洋集团冷链产品的配送是通过海安物流园（a）实施。海安物流园到各个需求地的交通示意图如图1所示，距离单位为km。

图1 需求企业的地理位置及相应距离

由冷链配送模型，海安物流园到各个需求地的装载方案分别见表10-表13。

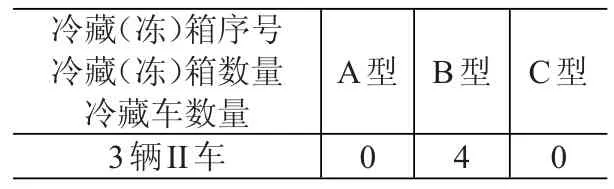
表10 a→b装载方案（单位：个）

表11 a→c装载方案（单位：个）

由冷链配送模型共指派I型车15辆、II型车3辆、III车21辆，运输总成本为25 524.65元。而中洋集团7月份实际指派I型车13辆、II型车6辆、III车18辆，运输总成本31 086.03元。利用冷链配送模型可节约5 561.38元。

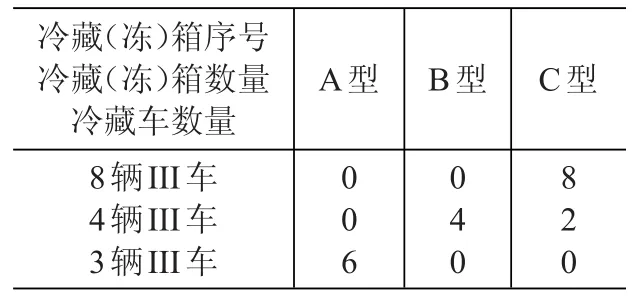
表12 a→d装载方案（单位：个）

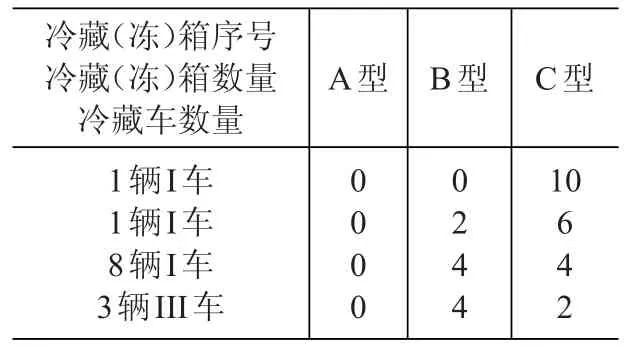
表13 a→e装载方案（单位：个）

［1］谭兆涛.浅述我国冷链物流的现状与提升［J］.肉类工业，2010，（3）:43-45.

［2］林道荣，周小建，陆志峰.冷藏箱货箱装载模型和算法［J］.南通大学学报，2006，5（4）:12-15.

［3］林道荣，陆志峰.部分货箱指定的集装箱装载模型和算法［J］.工程数学学报，2005，22（8）:20-24.

［4］姜启源，谢金星，叶俊.数学模型（第三版）［M］.北京:高等教育出版社，2008.

Establishment of Cold Chain Logistics Optimization Model

LinDaorong1，2，ZhangShun2，CaiChengfang1
（1.NantongUniversityXinglinCollege，Nantong 226007；2.SchoolofScience，NantongUniversity，Nantong 226019，China）

In this paper，from the characteristics of the cold chain products transported in the cold chain logistics process，we first considered the carton packing problem of the refrigeration trucks，then according to the practical demand of the destination and considering the situation of similar cartons or identical cartons，relied on prevalence and substitution to build other packing solutions and models；next，we studied the dispatching of the refrigeration trucks，divided their destinations into final destination and intermediate destination，and built the corresponding cold chain distribution optimization model；at the end，through an empirical investigation of the Jiangsu Zhongyang Group，we demonstratedthevalidityandcorrectnessofthemodelestablished.

coldchainlogistics；distributionmodel；heuristicalgorithm；refrigeration（freezing）truck

F252

A

1005-152X（2016）05-0119-07

10.3969/j.issn.1005-152X.2016.05.027

2016-04-09

国家自然科学基金项目（41276097）；2014年江苏大学生创新创业训练计划项目“南通冷链物流状况统计分析研究”（201413993006Y）；南通大学杏林学院自然科学基金项目“冷链物流优化模型构建”

林道荣（1963-），男，江苏海安人，教授，研究方向：组合优化；张顺（1990-），女，山东单县人，研究生，研究方向：运筹与控制；蔡成芳（1994-），女，江苏如皋人，研究方向：应用统计。