基于投入产出效率的应急物流中心选址

刘运昌，王绍仁，潘文军

（华侨大学，福建 泉州 362000）

基于投入产出效率的应急物流中心选址

刘运昌，王绍仁，潘文军

（华侨大学，福建 泉州 362000）

针对应急物流中心的建设特点与影响因素，提出ANP与超效率DEA相结合的方法，考虑定性指标之间的相互影响关系并将其定量化，应用超效率DEA对各方案的投入产出效率进行有效性排序，结合定性与定量因素，确定最佳方案并通过算例证明方法的有效性，从而弥补传统评价方法中忽略定性因素、主观影响过大、未进行有效性排序等方面的不足。

应急物流中心；选址；ANP；超效率DEA；投入产出效率

1 引言

突发性公共事件是指危害人民生命、财产、社会安全与稳定的突然爆发的事件，具有破坏性、不确定性、综合性、社会性、突发性和紧急性等特性［1］。进入21世纪，各种非常规突发事件充斥着人们的眼球，“9.11”恐怖袭击、俄罗斯人质事件、“SARS”、美国“卡特里娜”飓风等突发性公共危机严重地威胁着人类安全和社会稳定［2］。面对突发性事件，为防止灾情扩大，需短时间内调集大量物资，以安葬罹难者、救助民众、控制疫情、开展重建、恢复生产等。因此、加强应急物流建设有助于减少灾害损失，保障社会稳定。

2 文献综述

应急物流是以提供重大自然灾害、突发性公共卫生事件及公共安全事件等突发性事件所需应急物资为目的，以追求时间效益最大化和灾害损失最小化为目标的特种物流活动［3］。总体上、我国应急物流存在许多问题，如信息化程度较低、交通保障能力不足、配送体系有待健全、物资储备不够合理、有关法律规范缺失等［4］。经文献分析［5-6］，可知应急物流研究领域包括宏观和微观两类。

在微观领域，应急物流中心选址广受关注。应急物流中心是在应急物流网络中、在各应急保障基地内开展物流活动的货物集散或中转集中地，是构成物流网络基本结构的关键节点，其建设应遵循统一规划、高效性、经济性、信息化四条原则［7］，合理选址可以降低成本，保证应急物资的时效性，影响应急保障的效率和效果［8］。本文认为选址规划涵盖了规模、数量、位置等几个方面的安排，通过科学布局提高对灾害的响应速度与处理效率，减少损失，保障人民生命财产，增强区域安全性，因此选址研究具有理论意义与实用价值。

在方案制定方面，韦晓针对灾情等级不确定情况下应急物流的特点，构建了选址模型并用改进蚁群算法求解［9］。李国旗建立了考虑满意度和建设成本的选址规划模型并用模拟退火算法求解［10］。尹峰提出了多级覆盖的选址策略，构建模型并求解［11］。由此可知，选址方案的制定通常针对问题的定量因素，考虑单一目标或者多目标，运用算法求解，可获得在时效性、公平性、覆盖率或经济性等单方面具有一定优势的选址方案。但现实中选址涉及因素众多，包括社会、经济、技术、安全、环境等多个方面，因此必须全面评价选址方案，防止决策偏失。

在方案评价方面，常用的有AHP与ANP方法，利用它们进行指标设计并求出权重。例如，陈志宗在评价选址方案时设置4个一级指标：经济性、效率性、公平性、环境因素，包含投入成本、预算偏差等8二级指标［12］。蒋慧考虑选址的自然条件和社会因素，提出包括地质条件、交通条件在内的14个二级指标进行方案评价［13］。但主观因素影响较大使得上述方法受到限制，无法评价各选址方案的投入产出效率也令决策有失科学。因此、学者们结合DEA方法对选址方案的投入产出效率进行有效性分析，该方法尊重客观数据，不需提前设定参数以及人为比较权重，能避开主观因素影响。例如，杨锋考虑道路特性，利用DEA方法对应急设施的选址问题进行研究［14］。方磊建立了基于偏好DEA的多投入产出应急服务设施选址模型［15］。但两者研究中所选择的投入与产出均是定量指标，未考虑定性指标，针对此缺陷，宁艳梅利用AHP将选址因素中的定性指标量化，再用DEA进行评价［16］。张敏的研究方法与前者相似，但加入了整数规划进行最终决策［17］。其研究虽然引入定性指标，使评价更为全面，但仍存在两点不足，一是没有研究定性指标之间的相互影响关系，指标权重不够科学，二是未能对方案的投入产出效率进行排序。

因此本文提出ANP与超效率DEA相结合的评价方法，兼顾定性与定量指标，通过ANP网络描述定性指标之间的相互影响关系并将其定量化，获得定性指标的综合评价值即定性综合效益，弥补AHP方法对于指标之间的相互关系描述不足的缺陷；再通过超效率DEA计算各备选方案的投入产出效率并排序，弥补传统DEA方法在排序方面的不足，最后获得最佳方案并以算例证明方法的有效性。

3 模型构建

3.1 定性指标与ANP方法

房明名认为应急服务设施的规划和建设是一项系统工程，既要考虑国家政策、法律、技术规范、安全标准，又要兼顾到社会、经济、环境等方面的因素［18］。因此，在指标选择上，既要考虑其内在因素，如响应速度、覆盖率、设施容量等，还需兼顾外部条件。本文提出包含4个一级指标、9个二级指标的定性指标表，见表1。

表1 定性指标表

ANP由Saaty教授于1996年提出，基本思想是依据准则对元素组或者元素进行两两比较，处理后可得到各元素的相对重要性或各方案的优先权［19］。ANP网络由控制因素层和网络层组成，结合ANP思想，通过上述分析与咨询专家，最终确定表1所选的定性指标之间的相互关系，构成ANP网络如图1所示。

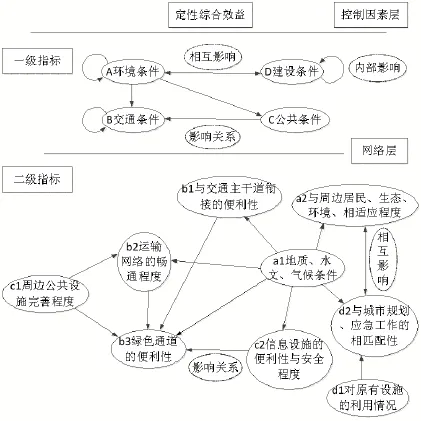
图1 定性指标关系图

确定各指标之间的关系后，依照ANP计算步骤求解各方案“定性综合效益”，步骤如下：

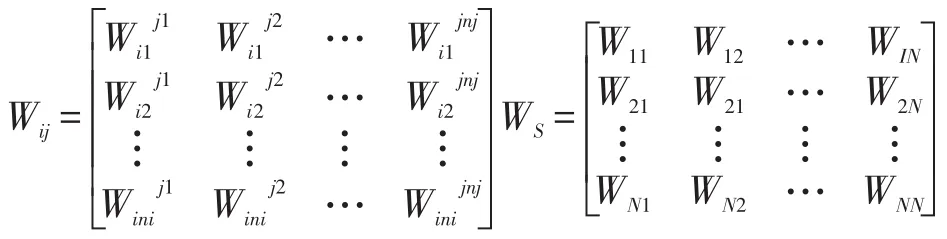
（2）构造加权超矩阵：以某准则PS为主准则，以元素组j为次准则，进行元素组两两比较，构造判断矩阵Aj并进行归一化处理得到若两元素组之间无影响关系，则由此可得到权重矩阵AS与加权超矩阵

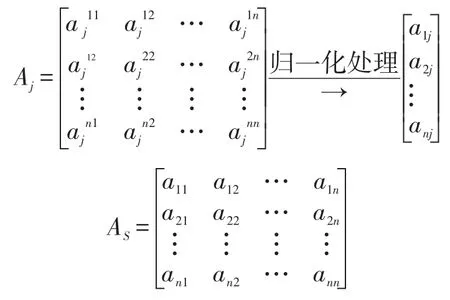
（3）计算极限超矩阵。极限超矩阵用于确定稳定元素优先权，将Wa做乘方运算需要反复迭代直到得到稳定的收敛矩阵。

（4）最终得到各方案“定性综合效益”的权重。

3.2 定量指标与超效率DEA

程赐胜认为选址涉及到多种复杂因素，是多目标决策性问题，并选取地价等10个输入输出指标进行研究［20］。曹庆奎则将DEA与灰色关联分析相结合，研究建设费用等7个投入产出指标的效率［21］。本文经综合考虑，设置定量投入、产出指标共5个，见表2。

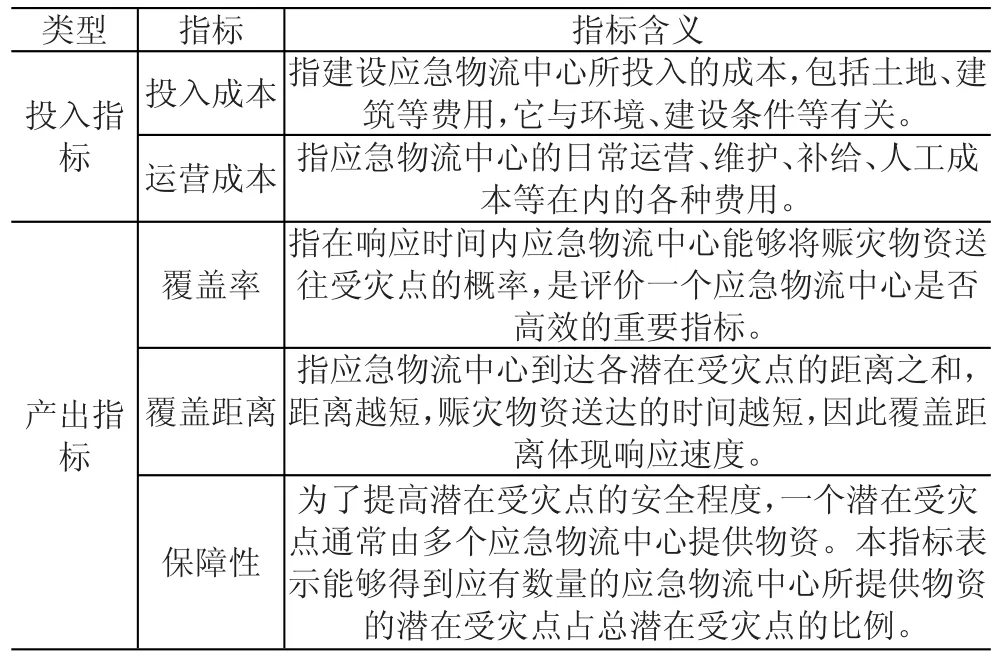
表2 定量指标表

将ANP方法求得的各方案“定性综合效益”的权重作为该指标的分值，纳入产出指标，最终获得以投入成本、运营成本为投入指标，以覆盖率、覆盖距离、保障性、定性综合效率为产出指标的超效率DEA指标体系。

DEA又称数据包络分析，由Charnes于1978年提出，具有不需预先估计参数、避免主观因素、简化运算过程、减小参数误差等优势［22］。传统DEA的C2R模型设有n个决策单元，m种输入，S种输出，记为决策单元为DMU。令Xij为DMUj中第i种输入的投入量，Yrj为DMUj中第r种输出的产出量为决策单元的效率值，S+、S-为松弛变量，λj为投入、产出系数，其模型如下。

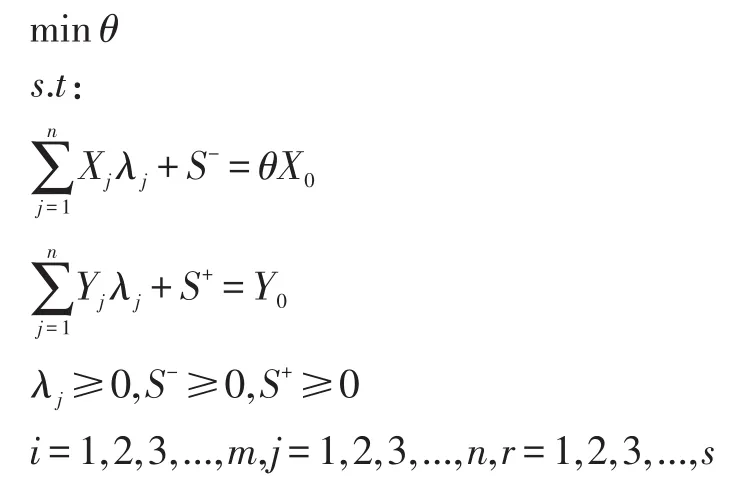
设模型的最优解为θ*、λ*、S*+、S*-。当θ*=1、S*+= S*-=0，则决策单元为DEA有效，当θ*=1、S*+≠0或S*-≠0，则决策单元为DEA弱有效，当θ*＜1或S*+≠0、S*-≠0，则决策单元为DEA无效。

传统DEA方法无法进行排序，局限性较大，因此Anersen于1993年提出了超效率DEA，基本思路是：在进行第K个决策单元评价时，将其自身排除于决策单元集合外，即通过以其他所有的决策单元投入和产出的线性组合代替第K个决策单元的投入和产出，令其超效率值可以大于1，原DEA无效的决策单元仍然无效［23］。超效率DEA可以对决策单元进行排序，其模型如下。

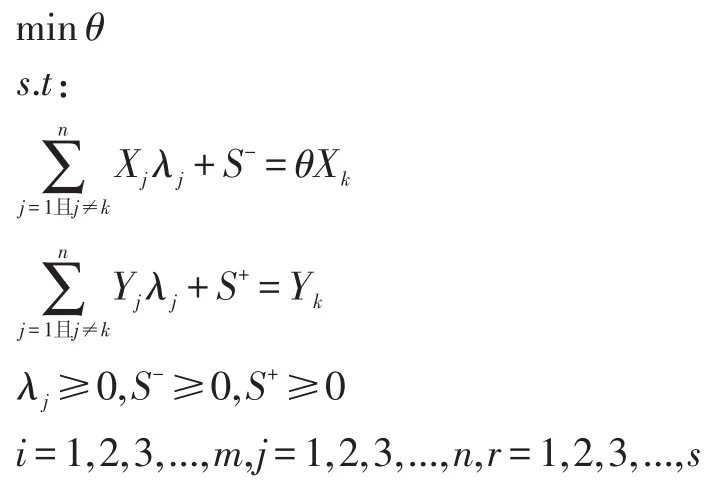
该模型中，当θ*≥1、S*+=S*-=0，则决策单元为DEA有效，当θ*＜1或S*+≠0、S*-≠0，则决策单元为DEA无效。通过超效率DEA求出各方案的投入产出效率并进行有效性排序，选择最佳方案。

4 算例分析

本文算例拟在某区域内建设一定数量的应急物流中心，综合考虑财政、土地等有限资源，现有十个备选方案，采用上述模型进行评价。

4.1 ANP阶段

根据ANP网络分析法，依照图1所示指标之间的影响关系，通过专家评分，比较指标之间的相对重要程度并采取Saaty创造的标度表，见表3。

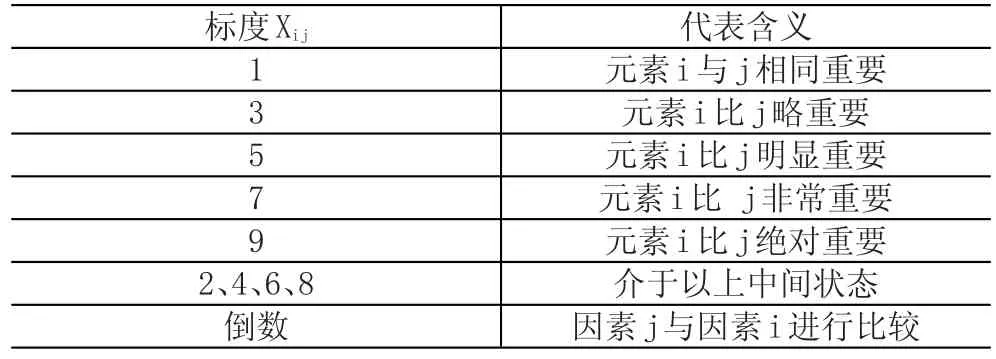
表3 重要程度标度表

（1）构造无权重超矩阵。例如二级指标中a1（地质、水文、气候条件）对于b1（与交通主干道衔接的便利性）、b2（运输网络的畅通程度）、b3（绿色通道的便利性）都有影响，可将其作为次准则，将定性综合效率为主准则，构造比较矩阵见表4。

表4 次准则地质、水文、气候条件下判断矩阵

由表4可得出，在一级指标交通条件内的二级指标中，绿色通道便利性的权重最大，证明其在三者中重要程度最高。对于二级指标绿色通道的便利性本身而言，还需要进行各备选方案的两两比较，判断各方案在此指标上的优劣，构造比较矩阵见表5。

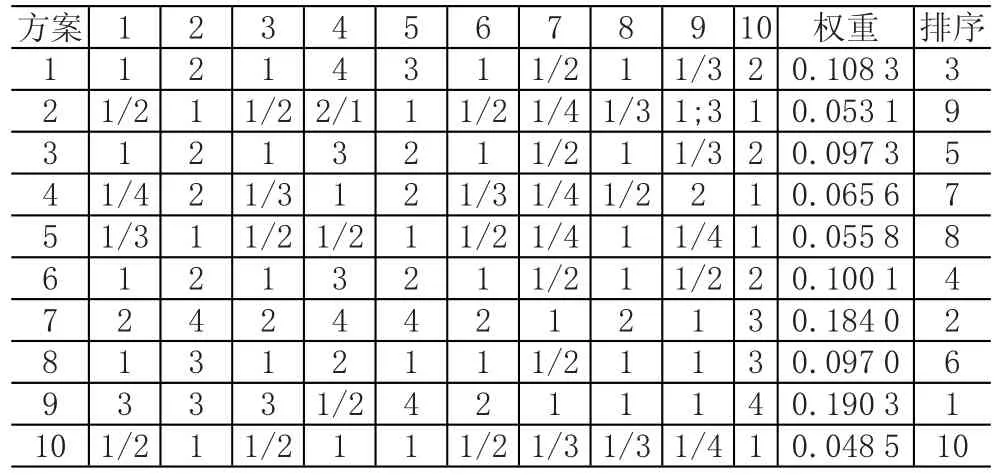
表5 次准则绿色通道的便利性下的判断矩阵

由表5可得出，方案9的权重最大，说明其在指标绿色通道的便利性上最具优势，即开辟绿色通道最为便利。按上述方式，根据二级指标相互影响关系，将归一化的权重向量一一构造出来，获得无权重超矩阵。

（2）构造权重超矩阵。例如以定性综合效益为准则，将一级指标环境条件、交通条件、公共条件、建设条件进行两两比较，构建比较矩阵，见表6。

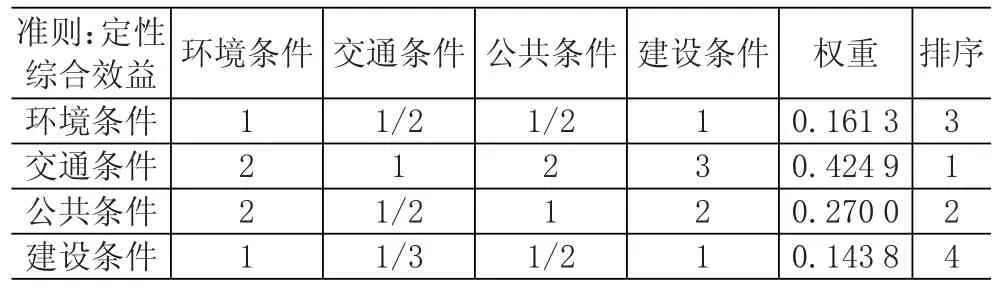
表6 准则定性综合效益下的判断矩阵

由表6可得出，交通条件占比重最大，说明其对于定性综合效益而言重要程度最高，其次是公共条件。按上述方式，根据一级指标相互影响关系，可将归一化的权重向量一一构造出来，获得权重矩阵。

（3）将无权重超矩阵与权重矩阵对应相乘，可得到加权超矩阵。

（4）加权超矩阵收敛成为极限超矩阵的过程复杂，本文运用软件Super decisions进行求解，计算结果见表7。

表7 各方案定性综合效益权重表

由表7可知，方案7的定性综合效益权重最大，说明方案7的定性指标整体效果最好，将定性综合效益纳入超效率DEA阶段的产出指标，其权重即为分值，进行下一步，求出投入产出效率有效性最佳的方案。

4.2 超效率DEA阶段

本算例中10个备选方案，其投入、产出指标数据见表8。

表8中包含2个投入指标，4个产出指标。其中产出指标值越大代表结果越好，但覆盖距离值越大表示应急物流中心到潜在受灾点所用时间越长，不利于救援工作，因此取该指标的倒数作为产出值。运用软件DEAP2.1进行计算，结果见表9。

表9 超效率DEA求解结果

由表9可得出，方案7、9、8、10、5、2的超效率值大于或等于1，为投入产出效率有效方案。方案7的效率值最高，为1.32，表示方案7即使再等比例增加32%的投入，在所有的决策单元中仍能保持投入产出效率的有效性。因此综合考虑，在本算例选择方案7为最佳方案。

4.3 算例分析结果

应急物流中心的建设具有弱经济性，但综合考虑选址时所涉及的各方面因素并评价其效率仍具有重要意义。算例最终选择的方案7，不仅拥有最佳定性综合效益，而且在一定的投入范围内可获得包括覆盖率、响应速度、救援水平、物资保障等在内的最大产出，在财政、土地等资源有限的情况下，将节约下来的人力、物力、财力用于赈灾救灾，体现应急物流中心的建设内涵。算例验证了本文提出的ANP与超效率DEA相结合的研究方法在进行应急物流中心选址方案评价等方面的可行性，对于合理规划应急物流中心，发挥其最大效益，获得最佳应急响应速度与物资输送水平，保障人民生命财产安全具有一定的意义。

5 结论

本文引入ANP与超效率DEA相结合的研究方法，分析定性指标之间的相互影响关系，构建ANP网络图，将定性指标定量化，求出各方案定性综合效益；利用超效率DEA法，充分尊重客观数据，以各方案的投入、产出指标分析其效率并进行有效性排序。该方法弥补了传统评价方法中的三点不足：（1）定性与定量指标不能兼顾；（2）未分析定性指标之间的相互影响关系，权重确定不合理；（3）未对方案的投入产出效率进行排序从而增强了选址决策的合理性。当然，本文在定性指标与定量指标之间的影响关系，定量指标权重等方面尚未深入，是未来需要继续研究的方向。

［1］祁明亮，池宏，赵红，等.突发公共事件应急管理研究现状与展望［J］.管理评论，2006，（4）:35-45.

［2］赵云锋.非常规突发事件的应急管理研究［D］.上海:复旦大学，2009.

［3］欧忠文，王会云，姜大立，等.应急物流［J］.重庆大学学报（自然科学版），2004，（3）:164-167.

［4］甘秋明，赵道致，王敏.供应链视角下应急物流中心选址研究［J］.综合运输，2015，（10）:68-73.

［5］王宁，王延章.应急管理体系及其业务流程研究［J］.公共管理学报，2007，（2）:94-99.

［6］李保俊，袁艺，邹铭，等.中国自然灾害应急管理研究进展与对策［J］.自然灾害学报，2004，（3）:18-23.

［7］聂彤彤.非常规突发事件下应急物流中心建设研究［J］.科技管理研究，2011，（14）:46-50.

［8］邹亮，徐峰，任爱珠.灾害应急设施选址规划研究［A］.中国城市规划学会.多元与包容—2012中国城市规划年会论文集（08.城市安全与防灾规划）［C］.2012.

［9］韦晓，常相全.基于改进蚁群算法的应急物流中心选址问题研究［J］.价值工程，2014，（17）:26-27.

［10］李国旗，张锦，刘思婧.城市应急物流设施选址的多目标规划模型［J］.计算机工程与应用，2011，（19）:238-241.

［11］尹峰，于永达.重大突发事件应急设施多级覆盖选址模型［J］.科学技术与工程，2014，（21）:302-305.

［12］陈志宗.城市防灾减灾设施选址模型与战略决策方法研究［D］.上海:同济大学，2006.109-119.

［13］蒋慧.应急物流配送中心选址研究［D］.成都:西华大学，2010.

［14］杨锋，梁樑，毕功兵，等.考虑道路特性的多个应急设施选址问题:基于DEA的研究［J］.管理评论，2008，（12）:41-44.

［15］方磊.基于偏好DEA的应急系统选址模型研究［J］.系统工程理论与实践，2006，（8）:116-122.

［16］宁艳梅.应急系统选址的模型与算法研究［D］.西安:西安电子科技大学，2007.

［17］张敏，杨超，杨珺.基于AHP/DEA的物流中心选址问题研究［J］.管理学报，2005，（6）:641-644.

［18］房明民.城市应急服务设施布局评价及优化模型研究［D］.长春:吉林大学，2011.

［19］王莲芬.网络分析法（ANP）的理论与算法［J］.系统工程理论与实践，2001，（3）:44-50.

［20］程赐胜，苏玲利.DEA法在物流中心选址中的应用［J］.长沙理工大学学报（自然科学版），2004，（Z1）:8-12.

［21］曹庆奎，李现美.基于灰色-DEA的物流配送中心选址研究［J］.河北工程大学学报（社会科学版），2013，（4）:7-10.

［22］魏权龄.数据包络分析（DEA）［J］.科学通报，2000，（17）:1 793-1 808.

［23］杨德权，裴金英.基于超效率DEA-IAHP的物流企业绩效评价［J］.运筹与管理，2012，（1）:189-194.

Location Allocation of Emergency Logistics Centers Based on Input-output Efficiency

LiuYunchang，WangShaoren，PanWenjun
（HuaqiaoUniversity，Quanzhou 362000，China）

In this paper，in view of the construction characteristics and influence factors of the emergency logistics center，we proposed a method that combined the ANP and the super-efficiency DEA，considered the mutual influence between the qualitative indexes and quantified them，next，using the super-efficiency DEA，ranked the validity of the input-output efficiency of the various plans，and then in connection with the qualitative and quantitative factors，determined the optimal solution and verified its effectiveness through a numerical example.

emergencylogisticscenter；locationallocation；ANP；super-efficiencyDEA；input-outputefficiency

F224；F252

A

1005-152X（2016）05-0086-06

10.3969/j.issn.1005-152X.2016.05.020

2016-04-12

教育部人文社会科学研究青年基金项目（12YJC630210）；华侨大学研究生科研创新能力培育计划资助项目

刘运昌（1992-），男，江西宜春人，华侨大学工商管理学院硕士研究生，研究方向：应急物流、决策科学；王绍仁（1979-），云南文山人，华侨大学工商管理学院副教授，硕士生导师，研究方向：应急物流、决策优化；潘文军（1976-），江苏淮安人，华侨大学工商管理学院副教授，硕士生导师，研究方向：供应链管理、物流管理。