社交网络中考虑遗忘机制的谣言传播
2016-10-29王彦本蔡皖东
王彦本,蔡皖东
(1.西北工业大学计算机学院,陕西西安 710072;2.西安邮电大学通信与信息工程学院,陕西西安 710121)
社交网络中考虑遗忘机制的谣言传播
王彦本1,2,蔡皖东1
(1.西北工业大学计算机学院,陕西西安 710072;2.西安邮电大学通信与信息工程学院,陕西西安 710121)
社交网络是当前最重要的信息传播媒体之一。近年来,由谣言传播引发的事件时有发生,因此有必要研究社交网络中谣言的传播规律。根据Ebbinghaus遗忘规律,研究遗忘机制对谣言传播的影响规律,建立了以遗忘率为指数函数形式的谣言传播模型。通过对4种人群建立平均场方程,计算了基本再生数,对模型的传播规律进行了理论分析。通过在社交网络中实验,研究网络中4种人群的变化规律,分析遗忘率函数的各参数对谣言传播的影响,并且将遗忘率为指数函数和常数形式做了对比。实验结果表明:遗忘率对传播者和免疫者的密度影响显著,初始遗忘概率越大,或者遗忘速度越快,谣言的传播力越弱;相对于遗忘率为常数的情形,遗忘率为指数函数形式时更符合谣言传播的实际情况。仿真实验验证了理论分析的正确性,并据此提出了谣言控制策略。此项研究有助于深入理解谣言的传播行为,可为网络舆论的传播过程及预测提供参考。
谣言传播;遗忘机制;社交网络;传播模型;遗忘规律
近年来,我国先后爆发了由谣言传播引发的群体性突发事件,严重扰乱了人们的生活秩序,影响了社会的稳定。大多数谣言尤其是恶意的谣言会造成社会恐慌,引起突发事件,甚至演化为恶性的群体事件,造成的损失超出了社会资源所能承受的能力。因此,揭示谣言传播的规律和特性,提出科学的应对策略,具有明显的意义。
国内外建立谣言传播模型方面的研究已取得了一些进展,此项研究大致经历了3个阶段:经典的谣言传播理论、考虑拓扑结构的谣言传播理论和考虑心理特征的谣言传播理论。尤其是考虑心理特征的谣言传播理论近年来得到研究者的重视。人们在研究谣言传播的规律时,一般使用了复杂网络理论和传染病动力学,如SIS(易感状态-感染状态-易感状态)[1],SIR(易感状态-感染状态-移除状态)[2], SEIR(易感状态-潜伏状态-感染状态-移除状态)[3]等模型。谣言在网络中的传播和网络的拓扑结构有密切的关系,例如在微博、移动社交网络中的传播有较大差别[4-6]。近年来,人们研究谣言传播时,较多考虑了心理因素,如记忆、怀疑、遗忘等因素对谣言传播的影响。Kawachi[7]研究了免疫者的记忆机制对谣言传播的影响,当免疫者想起相关的谣言时,会先判断该谣言的真假。Nekovee等[8]发现遗忘对谣言的传播产生很大的影响。Gu等[9]将遗忘机制同谣言传播理论相结合,结合SIS模型研究了谣言传播的过程。Zhao等[10]研究了遗忘和怀疑机制对谣言传播的影响。张芳等在文献[11]中总结了谣言传播模型的研究成果,并提出了将来的研究方向,尤其是心理特征对谣言传播的影响。Zan等在文献[12]中提出了谣言传播的反驳机制,并提出了带有反驳机制的谣言传播模型和其修正模型。文献[13-15]提出了带有可变遗忘率的谣言传播模型,并分析了遗忘率对谣言传播的影响。
以上传播模型在描述谣言的传播规律时存在局限性,原因在于:①谣言的传播和疾病的传播有很大的区别。传播动力学理论中疾病或病毒的传播是无意识的,感染者无法终止疾病或病毒的传播。而在谣言的传播过程中,人的心理因素,如遗忘机制、遏制机制[13]等,对谣言的传播有很大的影响。②在谣言传播的机理研究中,有的研究虽然考虑了遗忘机制对谣言传播的影响,但通常将遗忘率设置为常数。德国心理学家Ebbinghaus[16]研究发现,遗忘的进程并不是均匀的,记忆和遗忘是时间的函数,经过的时间越长,遗忘的概率越大,记忆的概率越小。
本文探索基于Ebbinghaus记忆遗忘规律的谣言传播机理,建立了谣言传播模型,计算模型的基本再生数,从理论上分析了模型的传播规律,并通过仿真验证该模型。
1 谣言传播模型
1.1遗忘规律
当前处于信息大爆炸时代,大量的信息使人们遗忘的概率大大增加。当谣言在人群中传播时,遗忘是基本的特征。Ebbinghaus研究发现,遗忘在学习之后即开始,而且遗忘的进程并不是均匀的,记忆量和遗忘是时间的函数。他用无意义音节作记忆材料,计算记忆和遗忘的数量,得到了记忆遗忘实验数据[16],如表1所示。
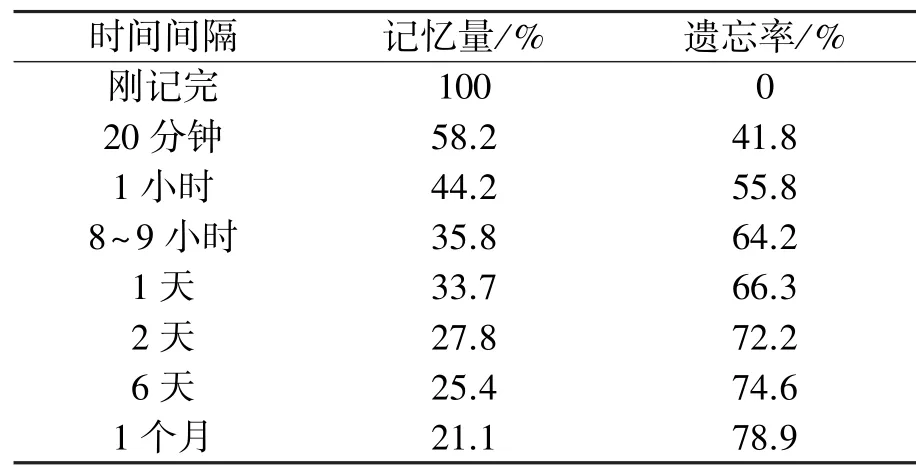
表1 Ebbinghaus记忆遗忘实验数据
Ebbinghaus记忆遗忘实验表明,随着时间的推移,保持的记忆量减小,遗忘的概率增大。根据实验数据来描述记忆和遗忘的规律,即Ebbinghaus记忆遗忘曲线。将该数据用曲线拟合函数进行拟合,发现遗忘率基本上呈指数规律变化[13],如图1所示。
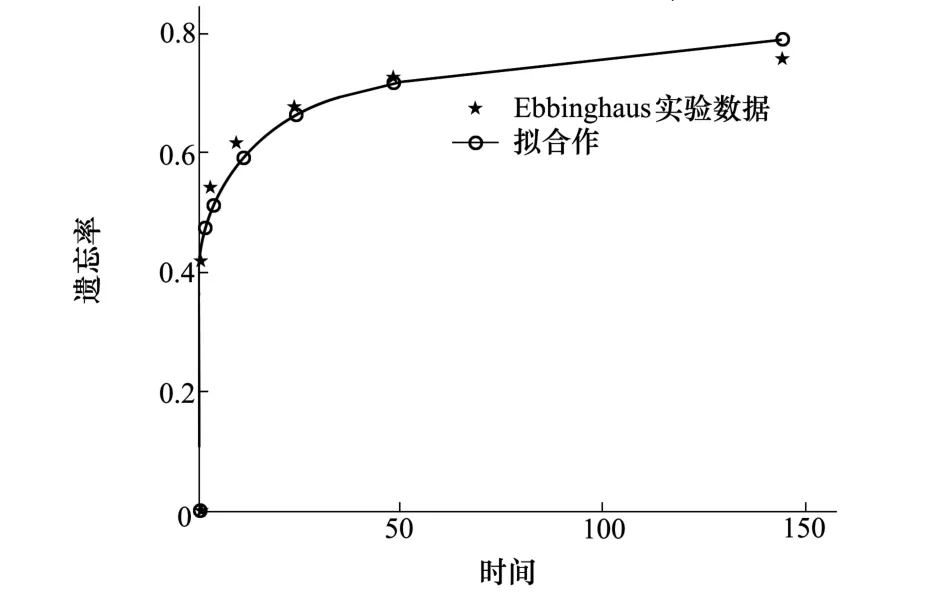
图1 Ebbinghaus遗忘率曲线
对于不同的人群,记忆遗忘特征可能有所差别,但基本规律是相同的。设遗忘概率函数为γ(τ),是一个人听到谣言后开始记录的时间,因此构建了遗忘概率函数如下:
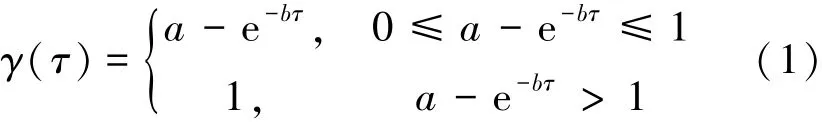
遗忘函数的2个参数a和b反映了遗忘率的2个特征:①一个人听到谣言后变为传播者时,τ=0,因此初始遗忘概率为a-1。a-1的值越大,谣言传播者的初始遗忘概率也越大,这反映了谣言不太重要,传播者容易忘记谣言。也就是说,a反映了谣言的重要性。②参数b反映了传播者的遗忘速度,b的值越大,遗忘速度也越大。
1.2谣言传播规则
假设每个人处于以下4种状态中的1种:未知者(Susceptible,S)、传播者(Infected,I)、知道谣言但不传播者(Know,K)和免疫者(Removed,R)。未知者表示还没有接触到谣言的节点,对谣言处于未知状态。传播者表示正在散布谣言的人。知道谣言但不传播者表示知道了谣言,但对谣言暂时没有传播的人。免疫者是指曾经听过或者知道这个谣言,对谣言传播失去兴趣,而永远不再传播谣言的人。由于接收过谣言的用户渐渐遗忘,传播节点发生遗忘后将成为免疫节点[17,19]。如图2所示,谣言在网络中的传播规则如下:
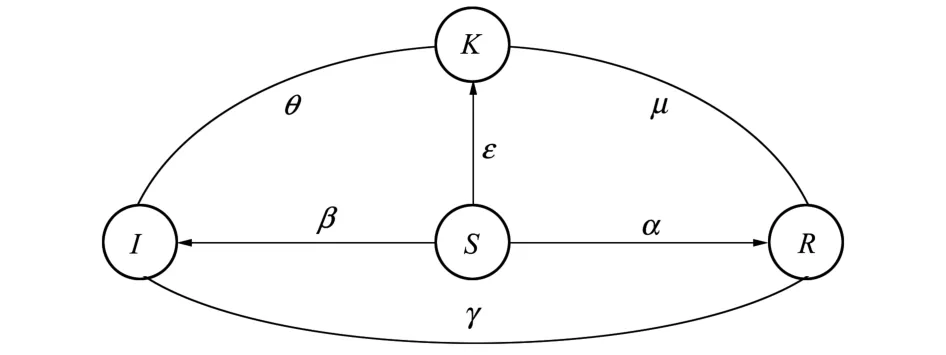
图2 考虑遗忘机制的谣言传播模型
1)分别定义S(t),I(t),K(t),R(t)为未知者、传播者、知道谣言但不传播者和免疫者的比重,显然有
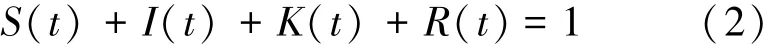
2)在谣言传播过程中,人数的迁入迁出及出生和死亡对谣言的传播影响甚微,因此假设总人数不随时间的改变而改变。
3)当未知者S与传播者I接触时,未知者S以概率β变为传播者I,以概率ε变为知道谣言但不传播者K,以概率α成为免疫者R。
4)知道谣言但不传播者K与传播者I接触时,K会以概率θ转化为传播者I,以概率μ转化为免疫者R。
5)传播者I传播谣言后逐渐失去兴趣,以遗忘率γ转化为免疫者R。
1.3建立模型
根据上述谣言传播规则,建立模型如下:

2 模型分析


2.1基本再生数
为了求模型的基本再生数R0,定义f和v如下[18]:

基本再生数R0=1是谣言传播的临界值。当R0>1时,网络中传播谣言的人数越来越多,造成谣言的大爆发。当R0<1时,传播者在网络中越来越少,最终将会消失。
2.2传播规律分析
由于遗忘率γ是时间的函数,随着时间的增加,遗忘的概率增大,因此基本再生数R0随着时间增加而减小。取β=0.2,a=1.1,b=0.2,得到基本再生数随时间的变化曲线,如图3所示。
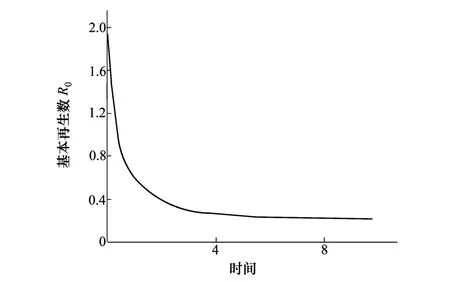
图3 基本再生数随时间的变化
由图3可知,起初基本再生数R0明显大于1。如果网络中有谣言传播者,此时谣言在网络中迅速传播。随着时间的增加,遗忘率增大,基本再生数R0会逐渐降低并小于1,并且趋于稳定。此时谣言传播者在网络中越来越少,谣言传播渐趋平息。
3 实验分析
本文根据Ebbinghaus实验数据,构建了指数函数形式的遗忘函数,在此基础上提出了谣言传播模型,并从理论上分析了传播规律。在后面的仿真实验中将验证该模型,分析遗忘机制对谣言传播的影响。
为了验证上述模型,我们使用matlab语言在社交网络上进行了实验验证。实验采用了www. epinions.com的who-trust-whom社交网络数据集,该数据集中的节点总数为131 828,边的数量为841 372,平均度为6.382 3,平均聚类系数为0.242 7,最长的最短路径为14。
3.1节点密度变化
初始时随机设置网络中只有0.5%的谣言传播节点,其余都是未知节点。在本次实验和接下来的几个实验中,均取相同的概率α=0.2,β=0.2,ε=0.2,θ=0.2,μ=0.2,以增加可比性。
取a=1.2,b=0.3,时间步为50,得到谣言传播如图4所示。由图4可以看到,最初人群中免疫者和知道谣言但不传播者的数量为零,只有少量的传播者,其他都是未知者。随着传播者开始散布谣言,未知者的数量快速减少,传播者的数量急剧增加。随着谣言的扩散,免疫者的数量也快速增加,而传播者和知道谣言但不传播者的数量分别达到一个峰值以后开始下降,最后网络里绝大部分为免疫者。
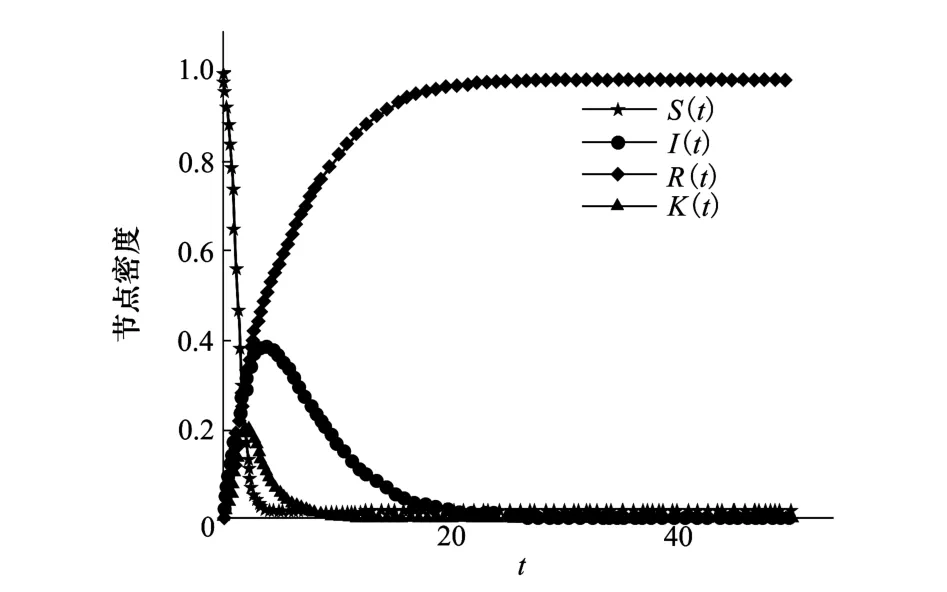
图4 考虑遗忘机制的谣言传播
3.2遗忘函数对传播者密度的影响
传播者数量的大小代表网络中谣言传播的活跃程度,是网络传播能力的体现,因此我们研究遗忘率对传播者数量的影响。取遗忘函数的参数b=0.2为固定值,参数a分别取不同的值1.2,1.4和1.6,得到不同的遗忘率对传播者数量的影响如图5所示。
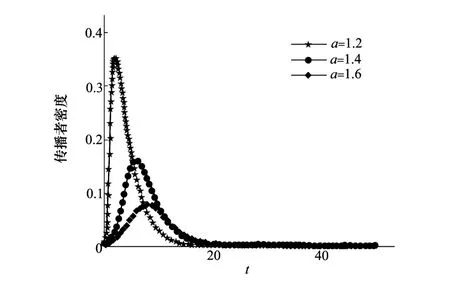
图5 初始遗忘概率对传播者密度的影响
由图5可以看到,随着网络中谣言的传播,传播者的密度首先快速增加,达到一个峰值,此时谣言传播者的密度最高。然后快速下降,最后逐渐趋近于零,意味着谣言传播的结束。参数a代表谣言的初始遗忘概率,也就是谣言的重要性,对传播者的密度影响显著,当a=1.2时,传播者峰值密度约为0.35。当a=1.6时,传播者的峰值密度约为0.08。因此a的值越小,谣言的传播力越强。
取遗忘函数的参数a=1.2为固定值,参数b分别取不同的值0.3、1.0和2.0,得到不同的遗忘率对传播者数量的影响如图6所示。
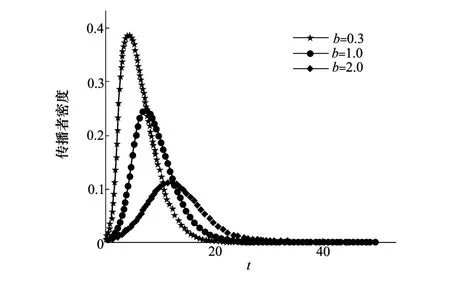
图6 遗忘速度对传播者密度的影响
由图6可以看到,参数b反映了谣言的遗忘速度,对传播者的密度影响显著。当b=0.3时,传播者峰值密度约为0.39。当b=2.0时,传播者的峰值密度约为0.12。因此参数b越小,谣言的传播力越强。
3.3遗忘率为指数函数和常数的比较
Ebbinghaus记忆和遗忘规律表明,遗忘的进程并不是均匀的,而是呈指数规律变化。免疫者数量的变化代表谣言消失的速度,我们研究遗忘率分别为常数和指数函数对免疫者密度的影响。遗忘率指数函数仍取a=1,2,b=0.2,因此遗忘率在[0.2, 1.0]之间变化。遗忘率为常数的情形取值为平均值0.6,如图7所示。
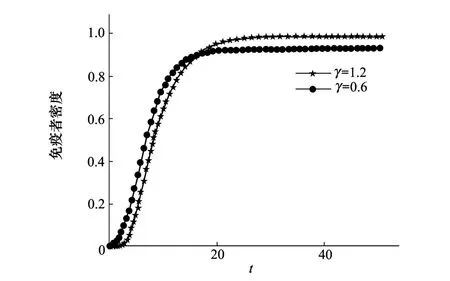
图7 遗忘率分别为常数和指数函数的免疫者密度
从图7可以看出,免疫者的密度先快速增加,经过一段时间以后,免疫者密度逐渐趋近于稳态值。遗忘率为指数函数时,在谣言传播的初始阶段,传播者的遗忘率较小,免疫者的密度也相对较小;在谣言传播的后期,传播者的遗忘率较大,免疫者的密度也相对较大。因此指数函数形式的遗忘率比常数形式更符合谣言传播的实际情况。
4 结 论
本文提出了一种在社交网络中考虑遗忘机制的谣言传播模型,以此研究遗忘机制对谣言传播的影响。本文的主要贡献在于:①根据Ebbinghaus遗忘规律,建立了遗忘率为指数函数的谣言传播模型。②建立了描述未知者、传播者、知道但不传播者和免疫者的平均场方程。③计算出基本再生数,并分析该模型的传播规律。④通过在社交网络中实验,分析了遗忘函数的各参数对谣言传播的影响。⑤对遗忘率分别为指数函数和常数2种情形的谣言传播做了对比。
通过实验分析,遗忘率对传播者和免疫者的密度影响显著,若初始遗忘概率越大,或者遗忘速度越大,则谣言的传播力越弱;相对于遗忘率为常数的情形,遗忘率为指数函数时传播者和免疫者的演化规律更符合谣言传播的实际情况。仿真实验验证了理论分析的正确性,因此第1节中给出的具有可变遗忘率的谣言传播模型具有合理性,能部分阐明谣言传播的内在规律。
根据谣言的传播规律,制定相应的谣言控制策略有显著的意义。为了减少谣言的影响,应尽量减少传播者的密度,增大免疫者的密度。传播者的初始遗忘概率反映了人们对谣言的重视程度,当谣言与人们的生活和利益相关性很大时,人们对谣言的重视程度很高,即认为谣言很重要,此时初始遗忘概率较小。当谣言的初始遗忘概率越大时,意味着该谣言不太重要,传播者更容易忘记谣言,传播者的峰值密度越小。传播者的遗忘速度也对传播者的密度影响显著,遗忘速度越大,传播者的峰值密度越小,谣言的传播力越弱。根据以上分析,控制谣言传播可采取以下策略:①第一时间公开谣言真相。当人们及时获得真相时,对谣言的重视程度降低,初始遗忘概率增大,从而减少了谣言的传播。②持续报道谣言的相关信息,让人们对信息的需求得到充分满足,传播意愿明显减小,遗忘速度增大,从而使得谣言的传播力变弱,人群中绝大部分成为免疫者。
本文的研究有助于深入理解谣言的传播行为,可为网络舆论的传播过程及预测提供参考。
[1] Leskovec J,McGlohon M,Faloutsos C,et al.Patterns of Cascading Behavior in Large Blog Graphs[C]//Prceedings of 2007 SIAM International Conference on Data Mining Minneapolis,Minnesota,USA:551-556
[2] 张彦超,刘云,张海峰,等.基于在线社交网络的信息传播模型[J].物理学报,2011,60(5):60-66
Zhang Yanchao,Liu Yun,Zhang Haifeng,et al.The Research of Information Dissemination Model on Online Social Network[J].Acta Physica Sinica,2011,60(5):60-66(in Chinese)
[3] Corporation H P.Impulsive Vaccination SEIR Model with Nonlinear Incidence Rate and Time Delay[J].Mathematical Problems in Engineering,2013(2):292-319
[4] 王辉,韩江洪,邓林,等.基于移动社交网络的谣言传播动力学研究[J].物理学报,2013,62(11):98-109
Wang Hui,Han Jianghong,Deng Lin,et al.Dynamics of Rumor Spreading in Mobile Social Networks[J].Acta Physica Sinica, 2013,62(11):98-109(in Chinese)
[5] 吴腾飞,周昌乐,王小华,等.基于平均场理论的微博传播网络模型[J].物理学报,2014,63(24):208902
Wu Tengfei,Zhou Changle,Wang Xiaohua,et al.Microblog Propagation Network Model Based on Mean-Field Theory[J].Acta Physica Sinica,2014,63(24):208902(in Chinese)
[6] 巩永旺,宋玉蓉,蒋国平.移动环境下网络病毒传播模型及其稳定性研究[J].物理学报,2012,61:46-54
Gong Yongwang,Song Yurong,Jiang Guoping.Epidemic Spreading Model and Stability of the Networks in Mobile Environment[J].Acta Physica Sinica,2012,61:46-54(in Chinese)
[7] Kawachi K.Deterministic Models for Rumor Transmission[J].Nonlinear Analysis Real World Applications,2008,9(5):1989-2028
[8] Nekovee M,Moreno Y,Bianconi G,et al.Theory of Rumour Spreading in Complex Social Networks[J].Physica A Statistical Mechanics&Its Applications,2008,374(1):457-470
[9] Gu J,Li W,Cai X.The Effect of the Forget-Remember Mechanism on Spreading[J].European Physical Journal B,2008,62 (2):247-255
[10]Zhao L,Qiu X,Wang X,et al.Rumor Spreading Model Considering Forgetting and Remembering Mechanisms in Inhomogeneous Networks[J].Physica A Statistical Mechanics&Its Applications,2013,392(4):987-994
[11]张芳,司光亚,罗批.谣言传播模型研究综述[J].复杂系统与复杂性科学,2009(6):1-11
Zhang Fang,Si Guangya,Luo Pi.A Survey for Rumor Propagation Models[J].Complex Systems and Complexity Science,2009 (6):1-11(in Chinese)
[12]Zan Yongli,Wu Jianliang,Li Ping,et al.SICR Rumor Spreading Model in Complex Networks:Counterattack and Self-Resistance[J].Physica A Statistical Mechanics&Its Applications,2014,405:159-170
[13]Zhao Laijun,Xie Wanlin,Gao H O,et al.A Rumor Spreading Model with Variable Forgetting Rate[J].Physica A Statistical Mechanics&Its Applications,2013,392(23):6146-6154
[14]王筱莉,赵来军,谢婉林.无标度网络中遗忘率变化的谣言传播模型研究[J].系统工程理论实践,2015,35(2):458-465
Wang Xiaoli,Zhao Laijun,Xie Wanlin.Rumor Spreading Model with Variable Forgetting Rate in Scale-Free Network[J].Systems Engineering-Theory&Practice,2015,35(2):458-465(in Chinese)
[15]顾亦然,夏玲玲.在线社交网络中谣言的传播与抑制[J].物理学报,2012,61(23):238701
Gu Yiran,Xia Lingling.The Propagation and Inhibition of Rumors in Online Social Network[J].Acta Physica Sinica,2012,61 (23):238701(in Chinese)
[16]Ebbinghaus H.Memory:A Contribution to Experimental Psychology[J].Annals of Neurosciences,2013,20:1151-1154
[17]Valerie Isham,Simon Harden,Maziar Nekovee.Stochastic Epidemics and Rumours on Finite Random Networks[J].Physica A Statistical Mechanics&Its Applications,2010,389(3):561-576
[18]Van den Driessche,P,Watmough,James.Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission[J].Mathematical Biosciences,2002,180(2):29-48
[19]王超,刘骋远,胡元萍,等.社交网络中信息传播的稳定性研究[J].物理学报,2014,63(18):180501
Wang Chao,Liu Chengyuan,Hu Yuanping,et al.Stability of Information Spreading over Social Network[J].Acta Physica Sinica,2014,63(18):180501(in Chinese)
[20]Wang Yanben,Cai Wandong.Epidemic Spreading Model Based on Social Active Degree in Social Networks[J].China Communications,2015,12(12):101-108
[21]Wang Ru,Cai Wandong.A Sequential Game-Theoretic Study of the Retweeting Behavior in Sina Weibo[J].Journal of Supercomputing,2015,71(9):3301-3319
Researching Rumor SPreading with Forgetting Mechanism Considered in Social Networking
Wang Yanben,Cai Wandong
(1.Department of Computer Science and Engineering,Northwestern Polytechnical University,Xi′an 710072,China
2.Department of Telecommunication and Information Engineering, Xi′an University of Posts&Telecommunications,Xi′an 710121,China)
Social networking is the most important medium for information spreading but incidents occur recently because of rumor spreading;so it is necessary to study how to reduce rumor spreading in social networking to a minimum.A rumor spreading model with forgetting mechanism considered is proposed in order to solve the problem of rumor spreading in social networking.In accordance with the forgetting rule of Ebbinghaus,we establish the model of exponential functional forgetting rate.The mean field equations of the model are established to describe the susceptible,the infected,know but not the infected,and the removed.The basic reproductive number is calculated and the spreading rules of the model are analyzed theoretically.We study the rules of four groups of throngs and analyze the influence of various parameters of forgetting function on rumor spreading.We compare the rumor spreading of exponential function forgetting rate and constant forgetting rate.The experiment results show that,the exponential forgetting rate can reflect the actual situation better:the forgetting rate has significant effect on the density of infected and removed,the greater the initial forgetting rate or forgetting speed,the weaker is the rumor spreading;compared with the case of constant forgetting rate,the exponential function forgetting rate is more in line with the actual situation of rumor spreading.The correctness of theoretical analysis is verified by simulation experiments and the control strategy of rumor is also proposed.The research results are helpful to understanding the behavior of rumor spreading and provide useful reference for the spreading process and the prediction of network public opinion.
algorithms,calculations,computer simulation,design,control,experiments,nonlinear analysis,nonlinear dynamical systems,social networking(online);forgetting mechanism,forgetting rule,rumor spreading,spreading model
TP393.0
A
1000-2758(2016)02-0349-07
2015-09-18基金项目:国家自然科学基金(61301091)与陕西省工业科技攻关项目(2015GY015)资助
王彦本(1977—),西北工业大学博士研究生,主要从事社交网络舆论传播的研究。
