基于正交分解技术的汽车非定常流场分析及重构

王国俊　崔文诗　周华　朱晖　杨志刚

摘要： 为有效开展汽车气动优化设计和主动流动控制技术，采用正交分解（Proper Orthogonal Decomposition， POD）技术分析汽车非定常流场中POD模态的物理意义，并利用重构技术建立汽车外流场瞬态简化模型.大涡模拟（Large Eddy Simulation， LES）仿真结果与实验结果的对比表明该仿真方法有效.POD分析结果表明：低阶模态主要对应分离泡的附着流动，包含流场中较高的能量；其他各个高阶模态含能相对较低，表征小尺度涡的作用.当保留前15阶POD模态时，通过重构技术可获得70%的原流场能量，得到的降阶模型可以较好地捕捉流动的特征.

关键词： 汽车； 非定常流场； 正交分解； 大涡模拟； 简化模型； Ahmed body； 流场重构； 涡能量耗散

中图分类号： U463.51； TB115.1文献标志码： B

Abstract： To carry out the automobile aerodynamic optimization design and the active flow-control technology effectively， the Proper Orthogonal Decomposition （POD） technology is used to analyze the physical meaning of POD modes in unsteady flow field around automobile， and a simplified transient model is built for flow field of automobile outer flow field. The Large Eddy Simulation（LES） results are compared with the experimental results to verify that the simulation method is effective. The POD analysis results show that， the low-order modes correspond to the attached flow of separation bubbles， which contains high energy of the flow field. Other high-order modes contain relatively low energy， which represents the effect of small scale vortex. If the first 15 order POD modes are retained， 70% energy of the original flow field can be obtained through reconstuction technology， the low-dimensional model can well capture the characteristics of the flow.

Key words： automobile； unsteady flow field； proper orthogonal decomposition； large eddy simulation； simplified model； Ahmed body； flow field reconstruction； vortex energy dissipation

0引言

汽车外形复杂，其运动流场是一个高阶非线性的复杂系统，存在着三维非定常分离流和近地面效应等复杂流动问题.汽车非定常流场对行驶稳定性、气动阻力、尾气传播和污染物夹带等[1]有重要影响，因此有必要将复杂流体动力系统分解并简化，得到主要流动结构，然后在此基础上进行高精度的流场重构，建立汽车非定常流场简化模型，进而实现高效的汽车气动优化设计和主动流动控制.

近年来，本征正交分解（Proper Orthogonal Decomposition，POD）技术被广泛应用于解决实验和数值模拟过程中的降维问题，如空气动力学、最优控制、结构动力学和热传导分析[2]等.POD技术是一种功能强大的降维和数据分解方法[3]，可在给出较高逼近度的情况下，有效降低物理问题的自由度，建立近似模型.因此，POD技术为高效分解和预测汽车非定常流场提供一种有效的工具.STH等[4]利用大涡模拟（Large Eddy Simulation， LES）对尾部倾角为90°的车体进行y向和x向速度计算，利用POD开展车体展向两侧涡脱落模式的研究.斜背后风窗对整车气动阻力和噪声影响较大[5]，但以往研究较少.国内外尚未开展基于涡量、压力等参数直接表征车辆气动性能的POD研究.

本文首先将数值仿真与实验结果比较，验证LES计算的有效性；然后，通过LES得到一系列快照的样本后，基于POD技术得到不同模态的拟序结构；最后，基于主要的流动结构建立斜背后风窗非定常简化流场（x和z向速度、涡量和压力），并与LES结果进行对比验证.

1数值仿真结果验证

1.1模型与仿真方法

以尾部倾角为25°的Ahmed body模型[5]为研究对象，采用0.7倍缩比的Ahmed body模型计算.缩比模型长L=0.731 m，宽W=0.272 m，高H=0.202 m，斜背后风窗长Lr=0.155 m，来流风速为25 m/s，雷诺数为1.2×106.根据模型尺寸，确定计算域长为8L，宽为7W，高为4H.为保证仿真准确性，设置第一层网格尺寸y+小于1，网格尺寸为0.3～1.5 mm，采用六面体网格对计算域空间进行离散，在流场变化较为剧烈的斜背和尾部进行网格加密以提高计算精度，体网格总数约为2 444万个，见图1.使用商业软件FLUENT 12.1进行LES计算，时间步长取0.000 1 s，迭代方法为SIMPLIC算法.

1.2仿真结果验证

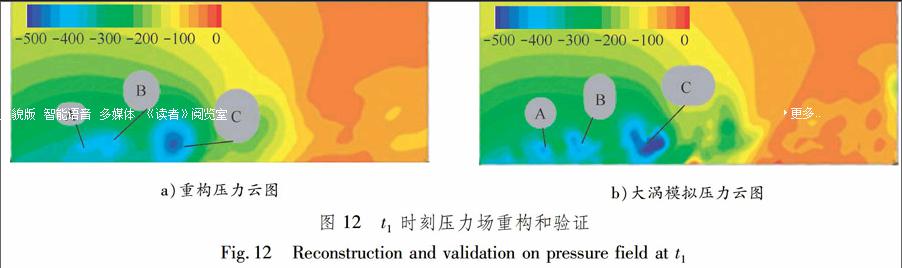
尾部平均压力系数仿真结果见图2.在z=0.17 m以下（车体尾部垂直背）和0.17 m

模型车身附近的几个涡脱落频率监测点示意见图3.对比实验与仿真结果的斯特劳哈尔数Sr=Hf0U-10，其中H为模型高度，f0为自然涡脱落频率.实验获得的Sr=0.2，LES得到的Sr=0.22，误差较小，因此可以认为此次仿真是有效的.

通过风洞实验，AHMED等[5]总结斜背倾角为25°的Ahmed body模型的气动阻力来源，认为阻力主要源于斜背的负压，而垂直背对阻力贡献较小.外流沿着车顶壁面向下游流动（见图4），气流附着在斜背上，实验中的气流附着位置更靠近斜背下缘，LES同样可捕捉到类似的流动现象.

2POD分析

2.1POD简介及其理论

POD方法于1967年首先引入到湍流流动结构研究中.[8]该方法的基本思想是把原来在时间域和空间域上的连续物理量场分解成只与时间和空间相关的函数展开序列，且其在均方意义上最优，在展开式中只需要少量的项数就可较准确地描述该物理过程，从而可以提供具有足够精度而自由度又少的低维模型，以降低计算维数、节省计算时间和内存.

A，B，C和D的坐标为：A（1.64，0.236）B（0.171，1.781）

C（1.807，0.228）D（1.664，0.294）

2.3POD分析结果

分别基于速度、涡量和压力的POD分析得到的模态数量皆为500，随着模态阶数的增多，含能降低.低阶模态通常代表流场中具有较高动能的大尺度流动结构，是整个流动的载体.1阶模态通常在流场发展中占支配地位，其含能最高，速度POD的1阶模态占总动能的16%，涡量POD的1阶模态占总动能的15%，压力POD的1阶模态占总动能的15%，皆远高于其对应的2阶模态.各变量的2～15阶模态含能占比皆超过1%，认为这些模态对流动仍有重要影响.速度、涡量和压力的1阶模态含能相差不到1%，2～7阶模态能量占比差异不大，8～15阶模态能量占比存在较小差异.速度、涡量和压力的前100阶模态各本征值占总动能的比例见图5.由此可知：不同变量的15阶模态含能总和皆在70%左右；随着阶数的增加，43阶模态后的每个模态能量占比皆趋近于0.由于高阶模态对总动能的贡献低，对应的是小尺度结构的作用，对流场的影响较低.每阶模态代表流动中不同尺度的流动结构.0阶模态代表时均速度场.速度模态表征脉动速度的分布，见图6.由此可知：1阶模态为速度场中的主要含能结构，包含流场的主要流动信息，其中x向速度模态更为清楚地展现上述流动现象；x和z向速度的2阶和3阶模态中高速脉动和低速脉动集中区呈现交替分布状态，z向速度模态中的交替结构更加明显.定义两高速脉动集中区（或低速脉动集中区）之间的距离为波长λ，通过图6e和6f可以清楚的观察到相邻模态之间高低速区以λ/4进行交替并向下游运动，文献[10]认为此现象与大尺度流动结构的耗散有关.

涡量的1阶模态为流场中的主要含能结构，其1阶模态见图7.由此可知：1阶模态对应的涡量分布形态对应斜背回流区.应该指出的是，高强度的涡量本身意味着高能量的消耗.y=0面涡量云图见图8.由图8可以看出：在斜背分离线处涡量大，随着流动往下游进行，这些漩涡逐渐分离，由能量较高的涡分离出能量较小的涡，在到x=1.8左右的时候，漩涡逐渐破碎，能量进一步耗散.1阶模态图直观地给出流场中能量消耗的主要来源.

基于静压的1阶模态也是流场中的主要含能结构.在图9a中，1阶模态中的负压区对应斜背回流区域，即为压力脉动在斜背附近空间的分布规律.在图9b和9c中，压力的2阶和3阶模态的高、低压力脉动集中区呈现交替分布，并向下游运动，这与基于z向速度的2阶和3阶模态结果类似，同样与大尺度流动结构的耗散有关.

3流场重构与验证

对含能贡献较低的高阶模态进行截断.根据对流场能量的需求，认为对包含70%能量的前几阶模态进行重构，可获得对流场较好的重构结果，即可简化流场.利用基于速度的前15阶模态进行重构，重构流场包含流场中70%的能量.速度场重构与验证见图10.

4结论

通过与实验结果相比，验证LES的有效性，进一步分析得到以下结论.

（1）相对于直接对非定常复杂流场进行分析而言，采用POD技术可以更加明确地辨别主导流动现象的主要流动结构.分别基于x和z向速度与涡量的POD分析指出：1阶模态含能最高，主要对应回流区的附着流动，是脉动能量的主要耗散来源；高阶模态含能相对较低，表征小尺度涡的耗散作用.

（2）在重构速度场中，当保留前15阶POD模态时，通过重构技术可获得70%的原场能量，得到的降阶模型能很好地重现斜背分离流中复杂的大小附着涡结构以及二次分离涡结构等非定常流动现象.

（3）基于涡量和压力POD的分析分别给出能量耗散的主要来源和压力脉动分布，可作为评价参数指导工程应用.参考文献：

[1]CHOI H， LEE J， PARK H. Aerodynamics of heavy vehicles[J]. Annual Review of Fluid Mechanics， 2014， 46： 441-68. DOI： 10.1146/annurev-fluid-011212-140616.

[2]SIROVICH L. Turbulence and the dynamics of coherent structures part I： coherent structures[J]. Quarterly of Applied Mathematics， 1987， 45（3）： 561-571.

[3]胡金秀， 郑保敬， 高效伟. 基于特征正交分解降价模型的瞬态热传导分析[J]. 中国科学： 物理学 力学 天文学[J]. 2015， 45（1）： 73-84.

HU J X， ZHENG B J， GAO X W. Reduced order model analysis method via proper orthogonal decomposition for transient heat conduction[J]. Scientia Sinica（Physica， Mechanica & Astronomica）， 2015， 45（1）： 73-84.

[4]STH J， NOACK B R， KRAJNOVIC′ S， et al. On the need for a nonlinear subscale turbulence a term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body[J]. Journal of Fluid Mechanics， 2014， 747： 518-544. DOI： 10.1017/jfm.2014.168.

[5]AHMED S R， RAMM R， FALTIN G. Some salient features of the time-averaged ground vehicle wake[DB/OL]. （1984-02-01）[2016-04-11]. http：//papers.sae.org/840300/. DOI： 10.4271/840300.

[6]KOURTA A， LECLERC C. Characterization of synthetic jet actuation with application to Ahmed body wake[J]. Sensors and Actuators A： Physical， 2013， 192： 13-26. DOI： 10.1016/j.sna.2012.12.008.

[7]MINGUEZ M， PASQUETTI R， SERRE E. High-order large-eddy simulation of flow over the “Ahmed body” car model[J]. Physics of Fluids ， 2008， 20（9）： 095101. DOI： 10.1063/1.2952595.

[8]BEN CHIEKH M， MICHARD M， GUELLOUZ M S， et al. POD analysis of momentumless trailing edge wake using synthetic jet actuation[J]. Experimental Thermal and Fluid Science， 2012， 46： 89-102. DOI： 10.1016/j.expthermflusci.2012.11.024.

[9]王掩刚， 陈俊旭， 先松川. 基于POD方法的二维方柱低雷诺数绕流流场分析研究[J]. 西北工业大学学报， 2014， 32（4）： 612-617.

WANG Y G， CHEN J X， XIAN S C. Analysis of low Reynolds number flow around a square cylinder based on POD method[J]. Journal of Northwestern Polytechnical University， 2014， 32（4）： 612-617.

[10]THACKER A， AUBRUN S， LEROY A， et al. Experimental characterization of flow unsteadiness in the centerline plane of an Ahmed body rear slant[DB/OL]. （2013-02-20）[2016-04-11]. http：//link.springer.com/article/10.1007/s00348-013-1479-5？no-access=true. DOI： 10.1007/s00348-013-1479-5.

（编辑武晓英）