误差激励作用下三维矩形液舱晃荡数值仿真

陈世文　杨志勋　杨钰城　阮诗论　岳前进

摘要： 原始激励的随机小幅变化会对晃荡载荷造成不确定影响，往往具有较强的随机性和非线性现象.通过计算流体力学（Computational Fluid Mechanics，CFD）方法构造三维矩形液舱载液率为85%的晃荡数值模型，并基于相同条件开展模型晃荡实验；通过追踪自由表面变化和晃荡冲击压力时程比较分析验证数值模型的有效性.基于原始激励构造一定误差变化范围（2%，5%和10%）内的误差激励，通过数值模拟分别提取拐角监测位置处的晃荡载荷时程曲线.研究结果表明：在不同误差激励下，虽然晃荡波形和频率基本一致，但压力峰值偏差与误差大小不呈现正相关效应，最大偏差约为33.17%；微小激励误差有可能对晃荡载荷结果造成较大的偏差影响.

关键词： 液舱； 液体晃荡； 误差激励； 冲击压力； 数值模拟

中图分类号： TE53； TB115.1文献标志码： B

Abstract： The radom slight change of original excitation would cause uncertain effect on sloshing load， which leads to strong stochastic and nonlinear phenomenon. A numerical model at 85% filling level is built for a 3D rectangle tank by Computational Fluid Mechanics （CFD） method， and the sloshing test is performed for the models under the same conditions； by comparing the free surface change and the time-history of sloshing impact pressure， the validity of the numerical model is verified. The error excitations with certain value （2%，5% and 10%） are given from the original excitation， under which the time-history curves of sloshing load of the detecting zone of the up-corner are obtained. The research results indicate that， there are similar sloshing wave form and frequency under different error excitation， but the deviation of pressure peak would not present positive correlation effect with error magnitude， and the maximum difference value is 33.17%； moreover， a slight excitation error would cause higher change of sloshing impact pressure error.

Key words： liquid tank； liquid sloshing； error excitation； impact pressure； numerical simulation

0引言

液体晃荡是一种非常复杂的流体流动现象，且具有很强的非线性和随机性.晃荡是普遍存在的一种自然现象，在海洋、船舶、航天和能源等工程领域也均有涉及，特别是在液化天然气行业.近年来由于浮式生产储油船和超大油船的装载量越来越大，伴随的晃荡冲击问题越来越严重.液舱在不同海况激励条件下的晃荡载荷成为液舱设计的一大难点和关键考虑要素.

影响晃荡载荷的因素较多，例如外激激励、载液高度及流体的物理特性（可压缩性、黏性和密度）等.不同的外激激励对晃荡载荷影响较大.THIAGARAJAN等[1]通过数值方法研究晃荡冲击压力和自由液面波高对激励频率、激励幅值和液体装载率等3个主要参数的敏感性.CAI等[2]通过实验和数值研究表明当液舱运动频率与流体的固有频率接近时，将会产生较大的冲击压力.NASAR等[3]研究不同的激励频率对晃荡频域的影响.这些分析研究大部分是在周期性激励下进行的，对于非周期运动激励的研究比较少.

从目前的研究可以看到，压力峰值的规律依赖于运动激励的可重复性.[4-5]实验手段可以很好地模拟晃荡物理现象，但实际操作中激励难免会出现误差，而误差激励相对原始激励的偏差对晃荡载荷规律影响的相关研究较少.以大连理工大学工业装备结构分析国家重点实验室的六自由度平台为参考：其承重能力为10 t，实际平台运动最大位移行程为±800 mm，经测量静态误差为±1 mm；转动最大角度行程±25°，静态误差为0.1°.通过大量的实验发现，实验并不能完全保证平台输入激励与平台输出激励完全一致，故本文通过数值模拟手段，运用流体体积法[6-8]研究运动激励误差变化与晃荡载荷的关系，研究结果对室内液舱模型晃荡实验有重要参考意义.

1数值模型

选取典型的三维矩形液舱为研究模型，其基本尺寸[9]见图1.在实际工程中，高载液率下晃荡冲击载荷一般较为严重，因此选择常见的危险载液高度即85%载液率作为研究对象.同时，高载液率情况下舱壁上拐角受到的抨击最大，因而选取图2所示位置作为晃荡载荷数据考察点.为保证计算精度，数值模型采用GAMBIT，选择六面体单元网格剖分，网格尺寸大小为总体结构尺寸的1%[10-12]，见图3.

2数值方法验证

为验证数值方法的有效性，选取同样的矩形液舱进行实验验证，保证晃荡实验与数值仿真采用一致的液舱尺寸、激励方式和初始条件，并针对相同的舱壁位置监测晃荡冲击载荷进行统计分析对比，从而验证数值模型.

2.1液舱与激励

实验采用大连理工大学工业装备结构分析国家重点实验拥有的六自由度平台，其可用于模拟船体单个或多个自由度的运动情况，见图4.基于数值模型液舱尺寸构建透明液舱，方便流场形态观察.参考数值模型载液率，加载85%的纯净水作为研究对象.同时，依据图2所示位置布置监测点并安装针孔式压力传感器，相互之间间距为10 mm×10 mm，以保证实验数据采样正确，方便后续对比.液舱运动激励采用与数值模拟相同的激励，即法国GTT公司所提供的C15横摇不规则运动激励谱[11].该系列运动谱被GTT鼓励作为全球范围内晃荡载荷基准性实验应采用的运动激励，目前诸多学者将其作为对晃荡现象研究的运动数据，其具体运动谱见图5.截取运动谱前60 s并对前20 s进行渐增处理，以更好地适应实验平台性能.

2.2结果对比分析

为更好地通过实验验证数值模拟的可靠性，分别对比液体晃荡过程中自由表面的变化情况以及监测位置的压力时程曲线.这2项是水波问题中常用的分析参数，可以直观地体现液舱晃荡问题时的晃荡冲击特性.相同激励下数值模拟与模型试验的自由表面对比见图6.

数值模拟和实验方法在各时刻的自由表面波形基本一致.在整个晃荡激励过程中自由液面的变化情况为：随着时间历程推移，横摇振幅不断增大，舱内液体晃荡现象逐渐剧烈；33 s时振幅第一次达到峰值，随后35 s时刻出现液面冲顶现象；此后，随着振幅变化相对持续平缓，晃荡维持上述现象不断往复；在45 s左右时由于振幅突然变小，晃荡现象出现小幅度下降，波的前后冲击暂时消失；而当50 s时刻附近振幅再次经过峰值，晃荡重新开始加剧，而且伴随着大量的碎波和夹杂空气现象，自由液面呈现的形态相对混乱，但整体轮廓与数值模拟结果仍然保持一致.由此可以认为该数值模型可以用于进一步对晃荡载荷进行研究分析，同时，采用数值方法还可以得到内部流场的速度信息.压力时程曲线对比是晃荡载荷检测的重要指标，其可以更加准确地量化数值方法的准确性.

为进一步验证数值模型可行性，原始激励下数值模拟获得的a1～a6监测位置压力时程曲线见图7.由此可知：各监测位置的压力时程曲线基本一致，其中最大冲击峰值约为静水压力的0.39倍，6个监测点压力峰值之间的最大差值约为静水压力的0.4%；从选取的监测位置来看，晃荡载荷的峰值在拐角附近分布相差不大.

选取晃荡冲击最为剧烈的时间段44～54 s，不难发现两者的压力时程曲线基本一致，但实验压力峰值相对数值求解较大，两者的晃荡冲击压力峰值相差约1.48%.虽然数值计算存在一定误差，但2种误差的综合作用结果仍然在研究的可靠范围内，从而验证后续工作的可靠性.液舱晃荡的自由表面波形变化情况同步对比较为一致，但由于局部碎波和强冲击时刻偏差的影响导致上述差异.

综上分析比较发现，与实验结果相比，数值计算得到的时值波动情况较弱，但整体的规律曲线一致，考虑到实验的误差与随机性，前述数值方法在一定程度内可以反映液体晃荡问题.

3矩形液舱晃荡敏感性分析

3.1误差激励

为研究激励发生偏差后对晃荡载荷的影响，通过随机参量小幅改变原始外部激励的峰值，将改变后的激励作为新的外部激励作用于液舱，得到相应的晃荡载荷.将新的激励定义为误差激励，见图9.假设原始激励每一周期的峰值为P0，i（i为激励中的周期数），存在均值为0.5的伪随机数组M{mi}（mi为数组元素，其数值为0～1的一位小数），通过表达式P1，i=（δ×mi+1）×P0，i转化获得新激励在各个周期的峰值载荷，其中δ为选定误差，本文考虑范围为1%～10%，由此得到的外激激励称为相应的误差激励.

3.2误差激励分析

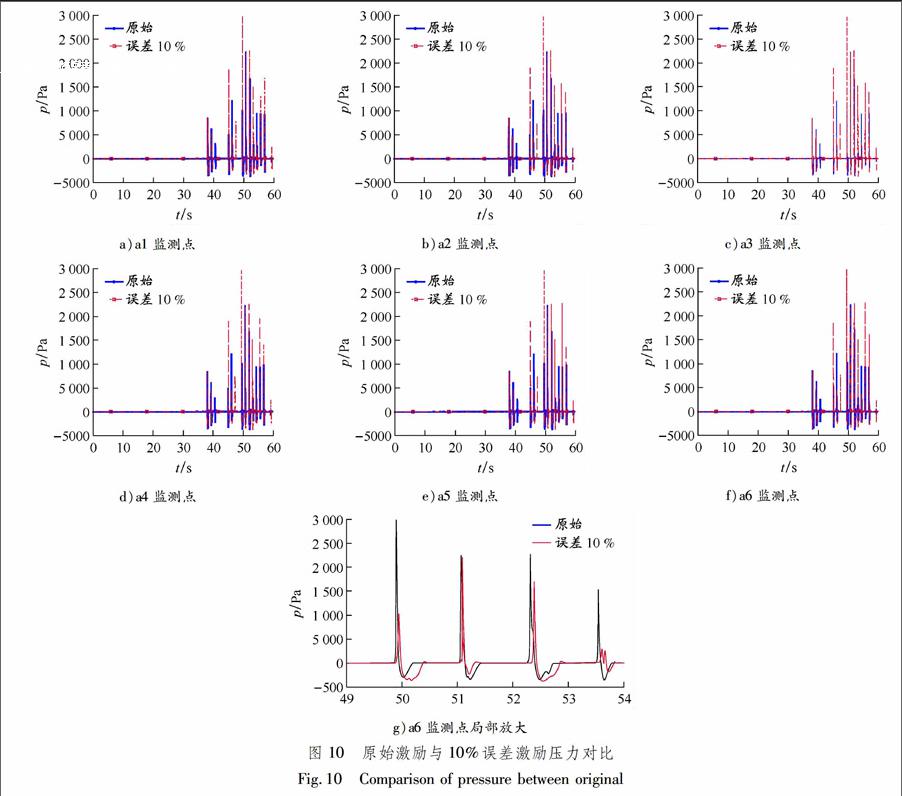
首先选取偏差为10%的误差激励对85%载液率的三维矩形液舱进行数值模拟，并将其晃荡载荷与原始激励结果进行对比.原始激励与10%误差激励在a1～a6监测点位置的压力时程曲线见图10.不难发现：两者压力时程曲线基本一致，压力峰值的变化基本与激励幅值同步；a6位置的局部放大图可以更加清晰地观察到晃荡冲击压力峰值与激励峰值基本发生于相同时刻，只是冲击峰值受激励峰值偏差的影响出现不同程度的波动.为更好地研究一定范围内误差激励变化对顶部监测位置的晃荡冲击载荷影响，考虑到液舱拐角监测点之间受到的抨击压力几乎相当，选取a1监测点作为研究对象进行数值模拟分析比较，其他位置同样可以得到类似结论.本文分别模拟2%，5%和10%误差激励作用下液舱的晃荡情况，分析冲击压力随时间变化曲线的特点以及压力峰值与原始激励结果偏差规律.

由图10不难发现，在该激励作用下，52 s时刻附近液舱受到的冲击压力最大.原始激励与2%，5%和10%误差激励作用下的液舱a1监测点该时间段晃荡载荷压力时程曲线见图11.

基于48～55 s区间段进行分析，可以看出误差激励与液舱晃荡的频率变化基本同步，并没有出现强烈的混沌现象.同时发现，本文中所定义的激励变化会使得载荷在峰值位置的时值发生变化，但对于整体晃荡周期和波形基本没有影响.

各误差激励下压力最大峰值及其相对原始激励偏差结果见表2.当误差激励为10%时压力峰值Pmax偏差最大为33.17%，说明由于误差激励所带来的压力峰值的变化较为明显.然而，激励误差大小与晃荡冲击压力偏差并不呈现正相关关系，虽然激励幅值增大，但其导致的晃荡冲击载荷有可能相对原始结果有所降低，例如5%误差激励所对应的结果.同时，误差激励对于晃荡载荷影响存在不确定性，即使很小的激励误差，都有可能对冲击压力造成显著影响，例如2%误差激励所对应的结果.单从压力峰值数值大小分析，其变化范围均在同一数量级，基本符合晃荡峰值的变化，说明该范围内误差激励未造成强烈随机现象.

4结论

针对三维矩形液舱，在系列误差激励下利用FLUENT进行数值模拟舱内晃荡问题，分析不同误差激励作用对液舱冲击载荷的影响，结论如下.

（1）基于流体体积法进行的三维矩形舱晃荡数值模拟，通过分析自由液面波形并对比试验结果，表明在没有出现碎波及弱冲击的情况下，其有效性和可靠性较高.

（2）在外激励作用下，三维矩形液舱上拐角受到较大的晃荡冲击载荷，各监测点压力呈现较好的一致性，峰值偏差范围在0.4%以内.从选取的监测位置来看，晃荡载荷峰值在拐角附近分布相差不大.

（3）本文所选取误差激励对于波形和周期的影响很小，但压力峰值偏差与误差大小不呈现正相关效应，压力峰值的变化范围在33.17%以内.

（4）从晃荡载荷的峰值对比分析中可以看出，由于晃荡载荷作用的随机性，即使微小的激励幅值误差都有可能造成较大的晃荡载荷偏差.

本文基于数值模拟对实验中存在的激励幅值误差对晃荡问题影响进行研究和分析，其结果对室内模型晃荡实验开展有重要参考意义.

参考文献：

[1]THIAGARAJAN K P， RAKSHIT D， REPALLE N. The air-water sloshing problem： Fundamental analysis and parametric studies on excitation and fill levels[J]. Ocean Engineering， 2011， 38（2）：498-508. DOI： 10.1016/j.oceaneng.2010.11.019.

[2]CAI Z H， WANG D Y， LI Z. Influence of excitation frequency on slosh-induced impact pressures of liquefied natural gas tanks[J]. Journal of Shanghai Jiaotong University（Science）， 2011， 16（1）： 124-128. DOI： 10.1007/s12204-011-1105-8.

[3]NASAR T， SANNASIRAJ S A， SUNDAR V. Liquid sloshing dynamics in a barge carrying container subjected to random wave excitation[J]. Journal of Naval Architecture and Marine Engineering， 2012， 9（1）： 43-65. DOI： 10.3329/jname.v9i1.7600.

[4]MEHL B， OPPITZ J， SCHREIER S. Sensitivity study on the influence of the exciting motion in liquid sloshing in a rectangular tank[C]//Proceedings of the 23rd International Offshore and Polar Engineering. Anchorage， 2013： 178-180.

[5]蔡忠华， 王德禹， 李喆. 液化天然气船液舱晃荡数值模拟与试验研究[J]. 上海交通大学学报， 2009， 43（10）： 1559-1563.

CAI Z H， WANG D Y， LI Z. Numerical simulation and experimental study of sloshing in a liquefied natural gas tank[J]. Journal of Shanghai Jiaotong University， 2009， 43（10）： 1559-1563.

[6]PARTOM I S. Application of the VOF method to the sloshing of a fluid in a partially filled cylindrical cotainer[J]. International Journal for Numerical Methods in Fluids 1987， 7（6）： 535-550. DOI： 10.1002/fld.1650070602.

[7]王永学， SU T C. 圆柱容器液体晃动问题的数值计算[J]. 空气动力学学报， 1991， 9（1）： 112-119.

WANG Y X， SU T C， Numerical simulation of liquid sloshing in cylindrical containers [J]. Acta Aerodynamica Sinica 1991， 9（1）： 112-119.

[8]PARK J J， KIM M S， HA M K. Three-dimensional sloshing analysis of LNG carriers in irregular waves[C]// Proceedings of the 15th International Offshore and Polar Engineering Conference. Seoul， 2005： 209-213.

[9]LOYSEL T， CHOLLET S， GERVAISE E， et al. Results of the first sloshing model test benchmark[C]//Proceedings of the 22nd International Offshore and Polar Engineering Conference. Osaka， 2009： 398-399.

[10]朱仁庆， 吴有生. 液舱内流体晃荡特性数值研究[J]. 中国造船， 2002， 43（2）： 15-21. DOI： 10.3969/j.issn.1000-4882.2002.02.003.

ZHU R Q， WU Y S. A numerical study on sloshing phenomena in a liquid tank[J]. Shipbuilding of China， 2002， 43（2）： 15-21. DOI： 10.3969/j.issn.1000-4882.2002.02.003.

[11]朱仁庆， 侯玲. LNG船液舱晃荡数值模拟[J]. 江苏科技大学学报（自然科学版）， 2010， 24（1）： 1-6. DOI： 10.3969/j.issn.1673-4807.2010.01.001.

ZHU R Q， HOU L. Numerical simulation of liquid sloshing in the tanks of LNG carrier[J]. Journal of Jiangsu University of Science and Technology （Natural Science Edition）， 2010， 24（1）： 1-6. DOI： 10.3969/j.issn.1673-4807.2010.01.001.

[12]GODDERIDGE B， TURNOCK S， TAN M， et al. An investigation of multiphase CFD modelling of a lateral sloshing tank[J]. Computers & Fluids， 2009， 38（2）：183-193. DOI： 10.1016/j.compfluid.2007.11.007.

[13]王福军. 计算流体动力学分析： CFD软件原理与应用[M]. 北京： 清华大学出版社， 2004.

（编辑武晓英）