基于倒立摆模型的四足机器人对角步态规划

郭鹏飞，王建中，施家栋

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

基于倒立摆模型的四足机器人对角步态规划

郭鹏飞，王建中，施家栋

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

为提高点着地四足机器人在匀速对角小跑过程中的动态稳定性，将对角小跑过程简化为一个倒立摆模型。；针对四足机器人对角小跑过程中由于重心无法始终处于支撑对角线上所引起的翻转，在此模型中转换为由于重心引起的摆动角误差；采用虚位移原理对机器人摆动角的变化进行分析，确定不同重心运动变化对摆动角误差的影响并找到合适的重心起始位置，理论上能够使摆动角的误差为零；动态仿真实验验证了所提出的对角步态规划能够使四足机器人实现稳定的对角小跑的有效性。

四足机器人；对角小跑；摆动角；倒立摆；步态规划

0 引言

四足机器人的对角步态作为一种占空系数比较小的步态，相对于爬行步态和溜蹄步态具有更快的运动速度。但是作为一种典型的高速运动方法，在对角支撑运动过程中，存在由于机体重心变化和腾空腿摆动造成的翻转力矩，从而使机器人的姿态产生变化。姿态的变化会引起腾空腿着地产生先后顺序，从而产生着地碰撞力，影响机器人的正常运动状态。随着落地姿态角误差的增大，碰撞力也会的增大，不仅会造成机器人的跳动改变运动方向，增大电机的负担，更有可能造成翻倒。因此如何对四足机器人对角步态进行合适的步态规划增强运动过程的稳定性防止翻倒是该研究亟待解决的关键问题。

日本的Inagaki K和Kobayashi H[1]对四足对角步态的翻转问题，提出了采用重力振子作为力补偿器的方法来平衡机器人的横向翻转力矩，但是没有对纵向翻转力矩进行平衡。上海交通大学的何冬青[2-3]提出了三分法，通过改变起始姿态的重心位置的方式来减小翻转角。南京航空航天大学的刘蕊[4]提出了类似的设置支撑足位置系数的方式来减小翻转角。但他们的模型都是在忽略腿部质量的情况下建立的，当腿部质量不能忽略时就会有较大的偏差[5]。谢惠祥[6]等提出了采用控制髋关节力的方式来对翻转角度进行控制。倒立摆模型现在主要在研究双足机器人[7-11]步行时有比较广泛的应用，由于四足机器人在对角小跑过程中是四足两两交替摆动向前运动，与双足机器人的步行非常类似，具有很大的借鉴意义。本文将四足机器人对角小跑过程中的翻倒问题与双足机器人的相似运动方式相结合提出了倒立摆翻转模型，并根据此模型方程对运动过程中的翻转的进行分析，确定能够实现理想对角步态的初始姿态和相应的对角步态，通过Pro/e与ADAMS联合仿真对模型以及相应步态进行仿真验证。

1 翻转倒立摆模型

当机体重心竖直投影不在支撑对角线上，以及摆动腿摆动时，就会产生绕对角线的翻转力矩，使机器人绕支撑对角线转动。在这里我们假设：

1)机器人以速度V匀速直线运动，地面水平无障碍。

2)机器人在运动过程中，支撑腿始终与地面接触无滑动。

3)机器人整体重心位置保持水平直线运动。

要实现稳定的匀速直线对角小跑，可知两组对角腿在运动过程中姿态完全对称，因此有足端初始前置S0=S/2。如图1所示a,b为四足机器人髋关节长方形的长和宽。2,3为支撑足，1,4为摆动腿。分别对腿1,4进行力学分析，如图2。摆动角速度分别为w1，w4。摆动角加速度分别为α1，α4。摆动角为θ1，θ4(与竖直方向的夹角，顺时针为负，逆时针为正)。在1,4腿足端轨迹一致时，有角度、角速度、角加速度完全相同。

图1 四足机器人初始四足位置与重心位置示意图

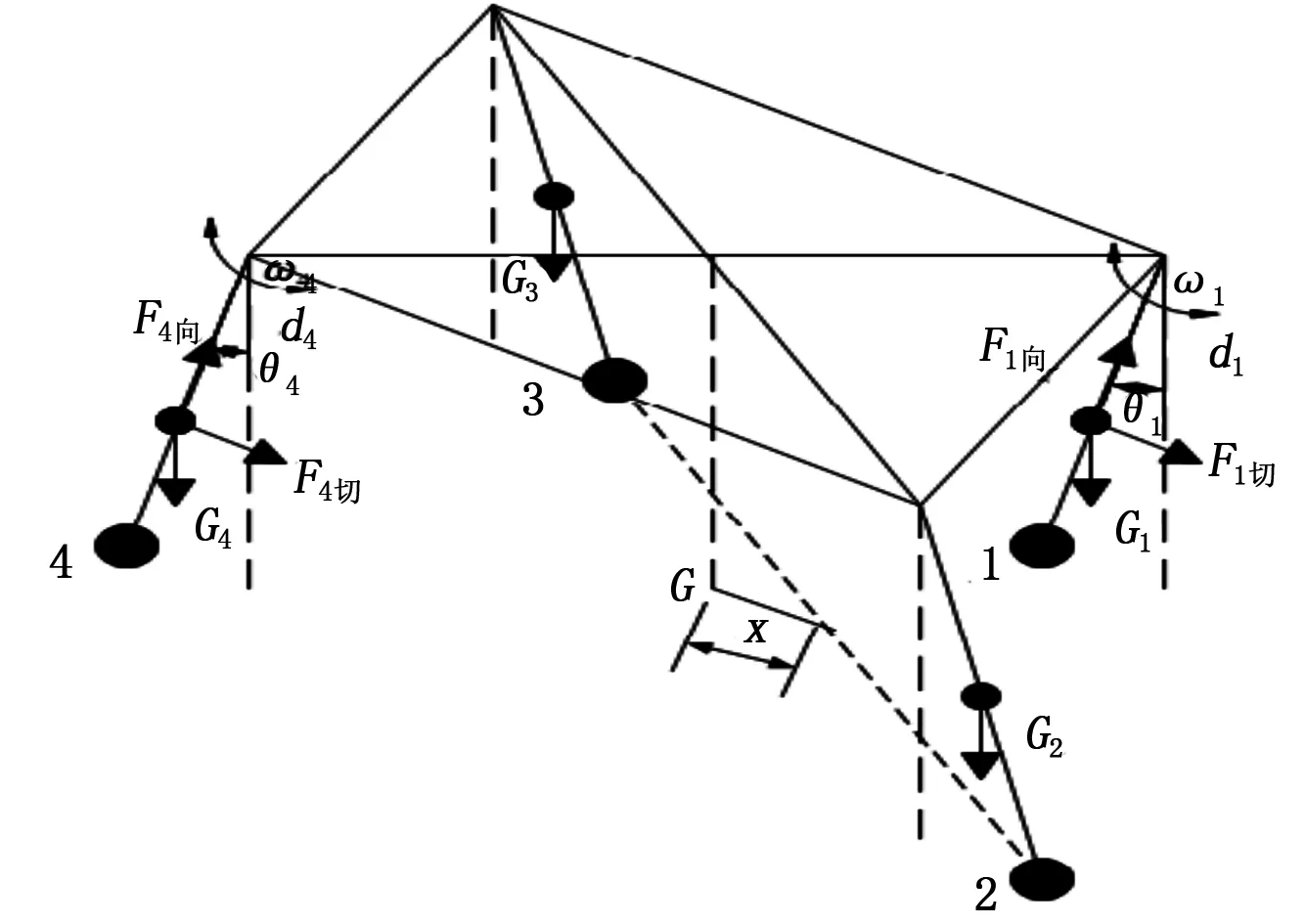
图2 四足机器人绕支撑对角线翻转模型

髋关节1处有虚位移原理知：

(1)

(2)

其中：

分别在竖直和水平方向的分量为：

(3)

同理在髋关节4处有：

(4)

对机器人躯干进行力学分析如图2所示有：

(5)

其中：

H1=H-Hcosθ1/2

H4=H-Hcosθ4/2

(6)

M，m分别为躯干和每条腿的质量，H为机器人高度。J为机器人绕支撑对角线的转动惯量，ε为机器人绕支撑对角线的翻转角加速度(逆时针为正)。l1,l4,H1,H4分别为腿1,4重心到支撑对角线的水平和竖直距离。

由w4=w1，θ4=θ1，α4=α1整理得到：

(7)

(8)

在没有T(θ4)即忽略腿摆动对翻倒的影响时有

(9)

(10)

代入式(9)对t积分有

(11)

再次积分有翻转角：

(12)

图3 重心在一个周期内的移动轨迹

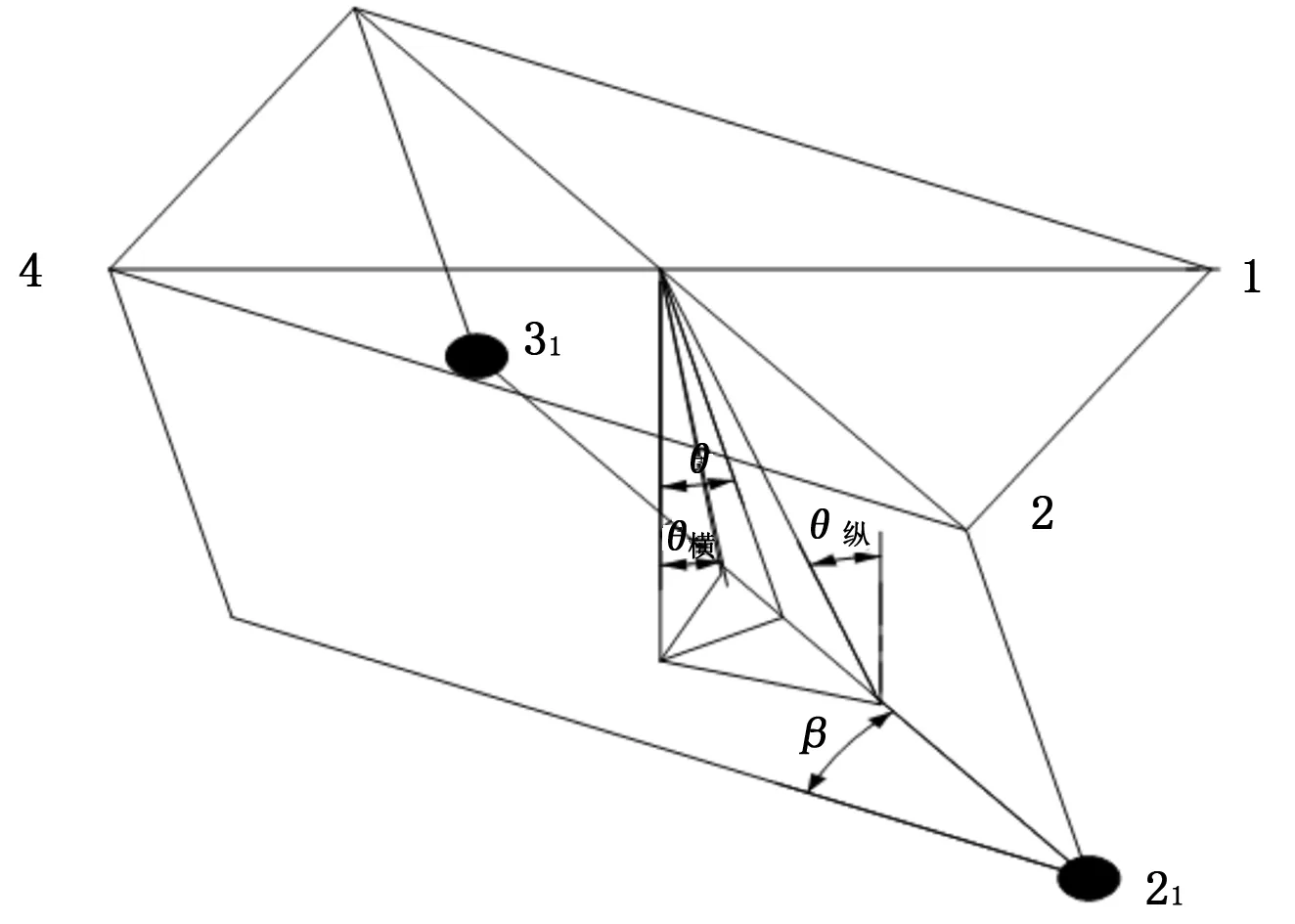
图4 机器人翻转角与横向与纵向翻转角示意图

如图4所示，横向和纵向翻滚角有

(13)

当θ比较小时有θ≈tanθ；则θ纵=θ/sinβ,θ横=θ/cosβ

在前进方向(纵向)有：

(14)

(15)

由式(14)可知要使四足机器人在摆动腿能够同时着地有

(16)

故：

(17)

(18)

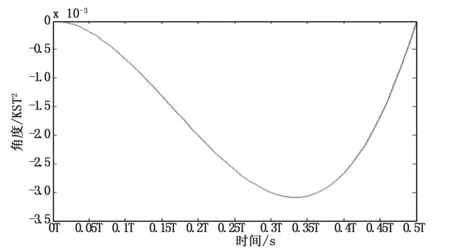
图5 摆动角第二项变化曲线

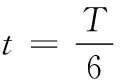
即

(19)

速度的取值范围为

(20)

2 对角步态规划

根据倒立摆模型理论分析得到了在不考虑T(θ4)影响下，能够实现匀速对角小跑对足同时着地的重心初始位置X，其中T(θ4)受摆动腿运动轨迹，机体转动惯量，摆腿转动惯量以及摆动周期的影响，可以通过测量相应摆动轨迹下摆腿对机体转动的转动角得到。在匀速对角小跑过程中，对足支撑与摆动切换位置如图1所示，2,3为落地腿的足端位置，1,4腿为摆动腿的摆动起始位置，重心在这一瞬间的位置为滞后支撑对角线X，重心运动速度恒定为v。摆动腿足端轨迹在机体坐标系内为正弦曲线

(21)

其中：h为抬腿高度，λ为步长，t为抬腿时间，T为机器人的步行周期。

3 仿真实验

为了验证采用倒立摆模型的正确性，采用pro/e与ADAMS联合建模如图6所示：机器人机体重16 kg，单腿重1.75 kg，总重量为23 kg；步长为200 mm，周期为0.5 s，tanβ=0.71，在水平地面上匀速直线行走，相应T(θ4)引起的摆动角误差范围为0～1.5°。

图6 四足机器人ADAMS模型

如图7所示，在前2 s为调整初始四足和重心时间，开始在经过一个到两个周期机器人速度达到预设值的时候，对足足端竖直方向轨迹几乎重合而且落地时刻基本一致，可知采用该模型步态即相对于四足直立状态，支撑对足足端前置s/2,重

心相对于支撑对角线滞后s/6时基本能够实现稳定的对角小跑。

图7 四足足端竖直方向运动轨迹

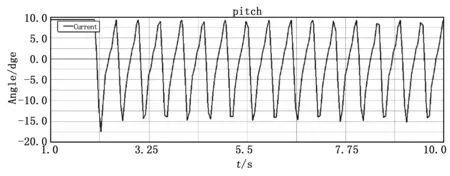
图8 机器人支撑腿摆动角度变化曲线

图9 机器人机体俯仰角变化曲线

4 结论

本文通过建立匀速对角小跑对支撑对角线的角动量方程，经过简化得到摆动方程。从仿生学的角度确定了初始支撑足的位置，根据摆动方程以摆动足的同时着地为出发点确定了初始重心位置与步长的关系。在机器人结构尺寸，质量分布等确定的情况下，对对角步态的允许速度范围进行讨论，分析了机构参数对对角小跑速度的影响。通过仿真实验表明在对角小跑过程中，机器人能够实现稳定的对角小跑，摆动角在一定的范围内稳定摆动。

[1] Inagaki K, Kobayashi H. Dynamical motion control for quadruped walking with autonomous distributed System[A]. Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems[C]. 1994(2):1004-1010.

[2] 何冬青,马培荪,曹 曦,等.四足机器人对角小跑起步姿态对稳定步行的影响[J]. 机器人，2004,26(6):529-532.

[3] 何冬青,马培荪,曹 曦,等.四足机器人对角小跑起步姿态对稳定性的影响[J].上海交通大学学报，2005,39(6):880-883.

[4] 刘 蕊，俞志伟，王 鹏,等.仿生四足机器人对角步态规划及稳定[J].科学技术与工程，2013,12(36):10852-10856.

[5] Schmiedeler J, Siston, R, Waldron, K. The significance of leg mass in modeling quadrupedal running gaits[A]. 14th Symposium on Theory and Practice of Robots and Manipulators[C]. Udine,Italy. 2002(1): 481-488.

[6] 谢惠祥 尚建中 罗自荣 薛勇 四足机器人对角小跑中机体翻转分析与姿态控制[J].机器人，2014,36(6):676-682.

[7] Wensing, Patrick M, Orin, David E. High-Speed Humanoid Running Through Control with a 3D-SLIP Model[A]. IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS)[C]. Tokyo, Japan. 2013(3): 5134-5140.

[8] 胡凌云，孙增圻.双足机器人步态控制研究方法综述[J].计算机研究与发展, 2015,16(5):728-733.

[9] 史耀强.双足机器人步行仿真与实验研究[D] 上海：上海交通大学, 2008.

[10] Motoi, Naoki, Suzuki, Tomoyuki, Ohnishi, Kouhei. A Bipedal Locomotion Planning Based on Virtual Linear Inverted Pendulum Mode[J].IEEE Transactions on Industrial Electronics. Bombay,India: IEEE 2009:54-61.

[11] Schweigart G, Mergner Y. Human stance control beyond steady stare response and inverted pendulum simplification[J]. Experimaental Brain Research,2008,185(4):635-653.

Diagonal Gait Planning for a Four Legged Robot Based on Inverted Pendulum Model

Guo Pengfei, Wang Jianzhong, Shi Jiadong

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology， Beijing 100081, China)

In order to improve the dynamic stability of the quadruped robot in the trot, an inverted pendulum model can be given by simplified the trotting. The center of gravity of the robot isn’t always up of the supporting diagonal which causes the turning. In the model, the turning angle is changed into the swinging angle which is caused by the Gravity. By using the principle of vitual displacement analysis of the influence of the center of gravity position on the swing angle error, a special point is found, which can make sure the robot swing error angle to be zero at the end of the swing. Dynamic simulation experiments show that the quadruped robot can run a stable trotting which verify the validity of the proposed planning method.

quadruped robot; trot; swing angle; inverted pendulum; gait planning

2016-01-14；

2016-02-29。

长江学者和创新团队发展计划(IRT1208)。

郭鹏飞(1988-)，男，博士研究生，主要从事机器人结构设计，机器人运动学与动力学方向研究。

王建中(1963-)，男，教授，博士生导师，主要从事地面无人作战平台方向的研究。

1671-4598(2016)07-0253-03

10.16526/j.cnki.11-4762/tp.2016.07.069

TP242

A