遥测振动信号EMD-WVD分布应用研究

王万金，张志国，徐洪洲

(中国人民解放军91550部队94分队，辽宁 大连 116023)

遥测振动信号EMD-WVD分布应用研究

王万金，张志国，徐洪洲

(中国人民解放军91550部队94分队，辽宁 大连 116023)

飞行器飞行试验采集的遥测振动信号频段丰富、成分构成复杂，合理有效地解读其包括的时频信息在分析飞行器结构和环境特性方面至关重要；依托经验模态分解(EMD)方法将复杂信号分解成准单分量信号，借助相关系数法将伪分量信号剔除，保证分解信号的有效性；通过EMD和 WVD方法的结合，将保留的准单分量信号进行WVD变换并做平滑伪处理，从而获得复杂信号的时频分布；EMD-WVD组合模型经在仿真信号上的应用检验，能够检测信号自身的时频特性，进一步应用其在遥测振动信号上，同平滑伪WVD抑制交叉项方法进行了比较，结果表明EMD-WVD组合模型更加有效，能够反映复杂工程信号的时频分布特性。

遥测振动信号;经验模态分解(EMD);Wigner-Ville分布(WVD);相关系数法

0 引言

飞行器从设计、研制、定型直至应用的过程需根据不同阶段的需求特点开展针对性试验，飞行环境的衡量和飞行状态的考核是其重要组成部分，需要借助无线遥测测量体制及相应的测控设备来实现。遥测振动信号是衡量飞行器飞行状态的重要参数，描述了其飞行过程中结构点、面的振动情况，应用相应的算法和结构信息能够给出飞行器飞行过程中的振动情况，准确有效地处理该类信号是遥测事后数据处理的重要工作。飞行器飞行环境和状态的多变决定了反应其状态信息的振动参数的非平稳性，对非平稳信号的处理，经典谱估计方法不能表示其时频特性，其表征了飞行器结构状态随时间的变化特征，在飞行器飞行试验结构健康状况鉴定中作用明显，合理有效地选择时频分析方法对遥测振动信号进行处理是数据处理工作的重要环节。Wigner-Ville分布(WVD)具有较高的时频分辨率，其时间和频率能够同时达到测不准原理的下界，是捕捉瞬态突变信号应用较广的时频分析方法，受其双线性表示理论基础的影响，对非单一信号将产生交叉项，而飞行器飞行试验采集的振动信号恰恰属于非单一信号，在先验信息缺乏的前提下，直接采用上述分析方法得到的处理结果难以直接判别信号的真实状况。因此，如何结合飞行器振动信号的特点，采取有效手段抑制交叉项导致的虚假信息是本文研究的重点，文中提出经验模态分解(EMD)和WVD结合的方法抑制交叉项的影响，通过合理确定相关系数阈值，剔除EMD过程伪分量的影响，达到有效分析振动信号时频特性的目的，通过仿真和试验数据分析，确定了方法的有效性和合理性，在飞行器飞行试验结构健康状况鉴定方面将发挥积极作用。

1 Winger-Ville分布(WVD)

魏格纳-威利变换(Wigner-Ville，WVD)，又称WVD分布，是采用对信号的双线性乘积进行核函数加权平均的方法来实现的非线性时频表示，它表示的是信号的能量密度分布，信号x(t)的WVD分布定义为：

其中：*表示复数共轭。WVD分布具有很多良好地性质，其中较高地时频聚集性使其在信号时频分析方面具有广泛地应用。遗憾的是，它却不满足可加性，考虑信号x(t)=x1(t)+x2(t)，它的WVD分布为：

可以看出，两个信号和的WVD分布并不是简单的两个信号各自的WVD分布之和，附加项2Re[WVDx1x2(t,ω)]通常称为交叉项。

2 经验模态分解(EMD)

2.1 经验模态分解(EMD)

经验模态分解方法定义信号都是由若干满足一定条件的单分量(IMF)构成，其中单分量需满足两个条件，一是每个IMF分量中极点数和过零点数小于等于1；二是单分量中任意一点，由局部极大、极小值点确定的包络线的均值为零。在满足上述条件基础上，EMD算法过程简述如下：

第一步，设置一定的步长，计算出信号s(t)的极大、极小值点，对其采用函数拟合获得原信号的上、下包络U(t)和L(t)，并计算其平均包络

将平均包络m1(t)从原信号s(t)中去除，新的信号序列记为：

第二步，判断h1(t)满足IMF条件是否成立，若成立，则原信号s(t)为IMF，否则重复第一步，直至找出满足IMF条件的信号为止，记为I1(t)。

第三步，将I1(t)从原信号中去除，对新的信号r1(t)重复第一步和第二步，直至找到第二个IMF分量I2(t)，循环往复，得到s(t)的个IMF分量，记

为残项，当其满足一定截止条件[1]时分解过程结束。原始信号s(t)可表示为：

(1)

在实际信号的分解过程中，若严格按照定义进行IMF分量的分解不可避免地将使产生的低频分量只具有调频或调幅属性，即为伪分量。因此，在工程应用中会采用一定的截止条件来控制分解过程，包括IMF分量和EMD过程两个截止条件。即便如此，由于受迭代次数和截止条件的综合影响，伪分量的产生亦是不可避免的，即若干低频IMF分量虽然满足EMD过程的定义，但并非原信号的真实成分，后文将采用相关系数法对其进行剔除处理。

2.2 相关系数法消除伪分量

相关系数是衡量两个随机变量之间线性相关程度的指标，其定义如下：

可以通过其来判断EMD过程分解的IMF分量同原信号的相关程度，达到剔除伪分量，保证分解分量能够真实反映原信号所包含的信息。相关度的阈值参数需要根据工程实际确定，一般认为相关系数绝对值在0～0.09之间为不相关，0.1～0.3之间为弱度相关，0.3～0.7之间为中度相关，0.7～1.0之间为强度相关。遥测振动信号本身复杂，在采用该方法剔除EMD过程产生的伪分量时，应根据工程实际来选取阈值参数，最大限度保证IMF分量的真实性。

3 EMD-WVD分布

WVD分布产生的交叉项是因为待分析信号包含多个频率成分，如果信号只包含单一频率成分则不会出现交叉项，且能够保持WVD分布良好的时频聚集性。利用EMD和WVD的结合，通过EMD将待分析信号分解成单分量信号，然后对单分量信号应用WVD分布求其时频分布，最后将各单分量信号的时频分布相加即可获得待分析信号的时频分布。EMD-WVD方法的过程为：

1)利用EMD方法将信号s(t)分解成若干只包含单一频率成分的分量,记为

使得其满足式(1)。

2)计算各分量Ii(t)(i=1…n)的WVD分布，即

3)将WVDIi(t,ω)求和，得到s(t)的EMD-WVD分布，

由于信号s(t)经EMD分解成不同的单分量信号来分别计算WVD分布，使得各单分量的WVD分布不受其它分量的干扰，能够有效地抑制交叉项的产生，且保持了WVD分布较高的时频分辨率。该方法的优点是通过对单分量的WVD分布结果进行叠加获得信号s(t)的时频分布，避开WVD分布交叉项影响的同时保持了良好的时频聚集性。

4 示例分析

4.1 仿真信号

一个典型的具有周期性、脉冲峰值、噪声以及调频和调幅为背景的非线性、非平稳机械振动信号可描述为：

x(t)=1.2sin(2π400t)[1+0.2cos(2π50t)]+0.8sin[((2π150t))+sin(2π30t)]+2.5sin(2π900t)+p(t)+y(t)

其中，采样频率为6 400 Hz，采样点数为1 024，采样数据序列时长为0.16 s，p(t)是脉宽为两个采样周期，幅值为3，中心分别位于0.04 s和0.12 s处的三角脉冲，y(t)是均值为零，方差为0.01的随机噪声，该信号时域波形如图1所示。

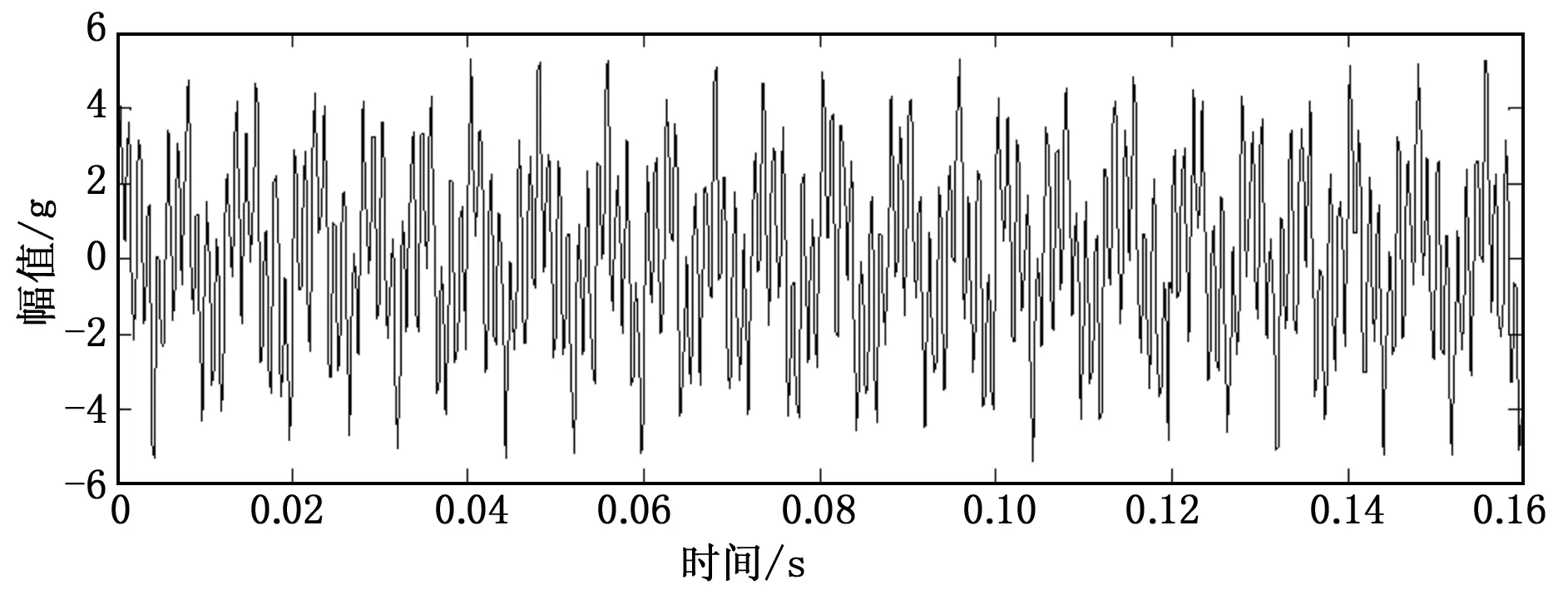
图1 仿真信号时域波形

图2为上述仿真信号经平滑伪WVD变换的时频分布结果，可以看出经过平滑伪过程抑制WVD交叉项的变换，能够分辨出信号中所含的900 Hz主频信息和150 Hz主频的调频信息，尽管400 Hz主频信息能够分辨出来，但其调幅特性辨别不够明显。

图2 仿真信号平滑伪WVD分布

图3为仿真信号经EMD分解获得的IMF分量，其中IMF8为残余项，IMF1-IMF7为分解获得的单分量，对各IMF分量与原信号进行相关性分析，相关系数分布如图4所示，可以看出IMF1-IMF3相关系数大于0.01，而IMF4-IMF7的相关系数小于0.01，判定IMF1-IMF3与原信号相关，其余不相关，即为伪分量。对IMF1-IMF3分别进行平滑伪WVD变换，其时频分布如图5所示，不难看出其体现了900 Hz主频特征、150 Hz主频的调频特征和400 Hz主频的调幅特征，与图1所示的仿真信号所包含分量的特征一致，且与图2分布结果比较看EMD-WVD组合模型的分布结果更能体现原信号的时频特征。

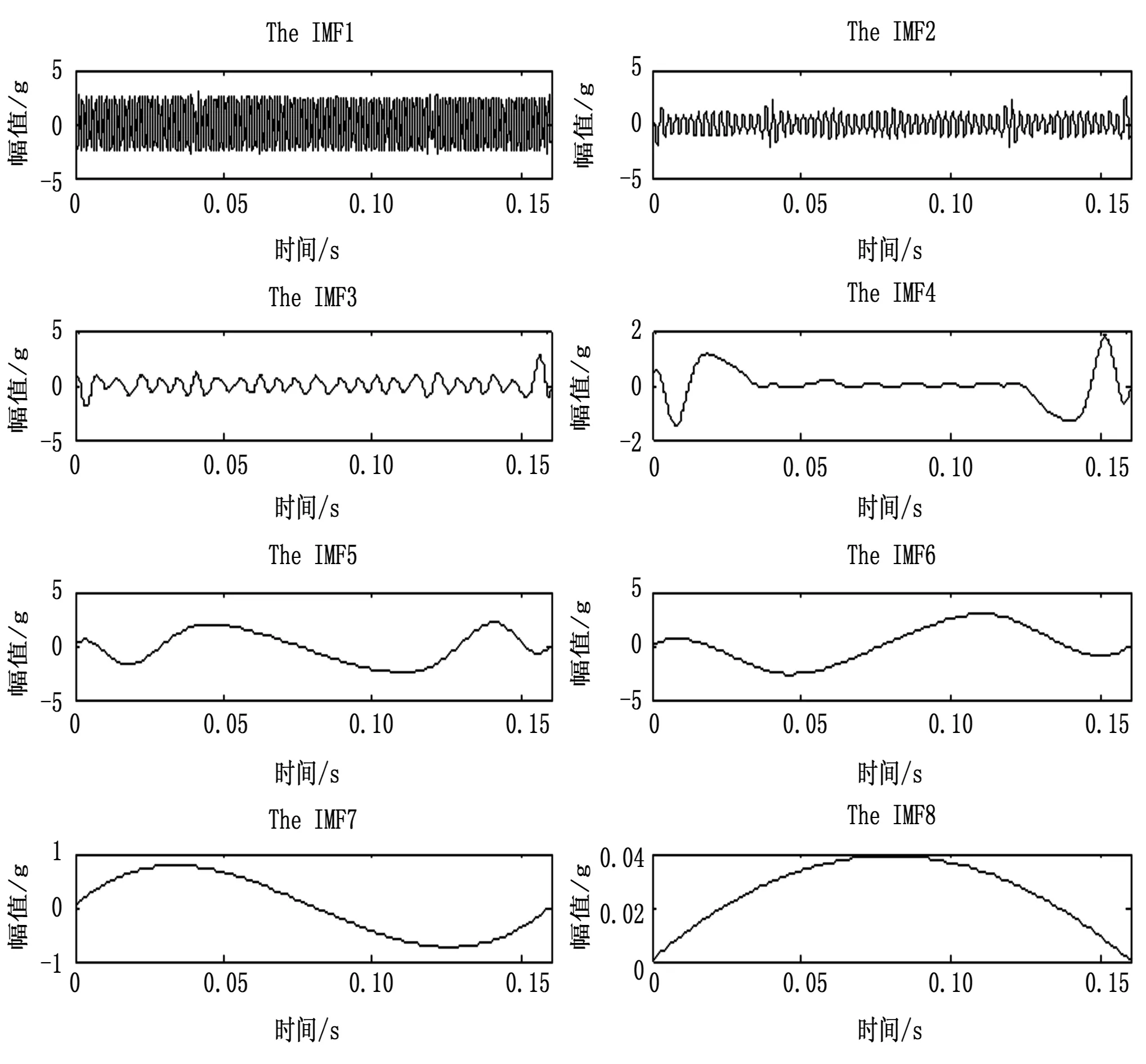
图3 仿真信号EMD分解的IMF分量

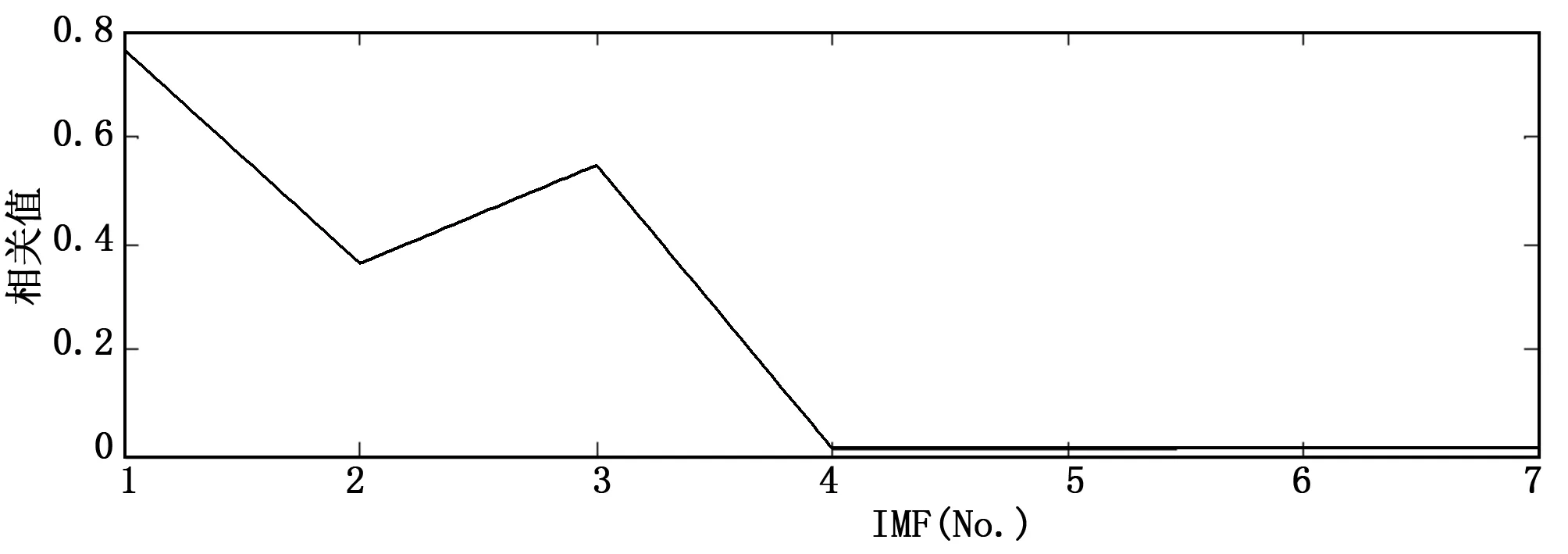
图4 仿真信号各IMF分量与原信号的相关性

图5 仿真信号EMD-WVD分布

4.2 实测信号

图6为某次飞行器飞行试验采集的遥测振动信号时域波形，采样序列长度为0.1 s。

对图6所示信号进行平滑伪WVD变换，时频分布如图7所示，从结果看上述实测信号包含了100～800 Hz的频率成分，对应时刻在0.018～0.091 s，且能量较大的频率成分主要集中在低频(150 Hz)部分。

图6 实测信号时域波形

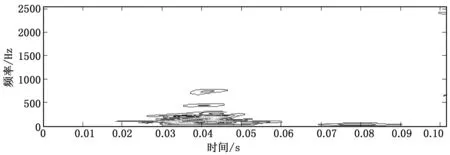
图7 实测信号平滑伪WVD分布

对图6所示信号进行EMD分解，获得的IMF分量如图8所示，其中IMF8为残余项，IMF1～IMF7暂且认为有效的准单分量信号，将各IMF依次与原信号做相关性分析，相关系数分布如图9所示，可以看出从IMF4之后的相关系数迅速减小，IMF5～IMF7的相关系数都小于0.15，根据工程经验，可以认为其为伪分量，予以剔除，即认为IMF1～IMF4为原信号所包含的准单分量。将IMF1～IMF4分别进行平滑伪WVD变换，时频分布如图10所示，从结果可以看出原信号所包含的频率成分主要集中在100～250 0 Hz，对应时刻在0.01～0.1 s，能量较大的频率成分依然集中在低频(150 Hz)部分，这与图7所示结果是一致的，但在0.095～0.1 s之间的时频分布是图7所没有体现的，其同样为原信号所包含的信

图8 实测信号EMD分解的IMF分量

息。综合分析，有理由说明EMD-WVD组合模型在实测信号上的应用是优于平滑伪WVD分布的，能够较为真实的反应原信号所包含的复杂频率信息。

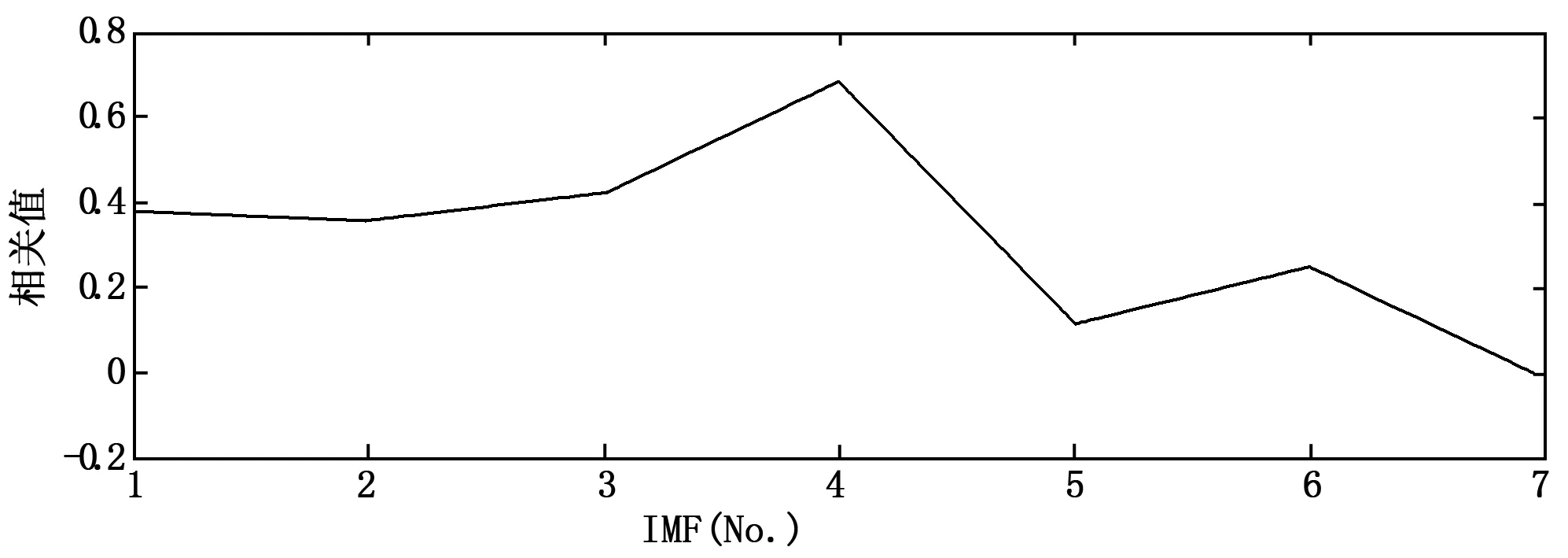
图9 实测信号各IMF分量与原信号的相关性

图10 实测信号EMD-WVD分布

5 结论

WVD分布具有较高的时频分辨率，能够分析复杂信号的时频特性，由于其双线性分布特性对于多分量信号而言将产生交叉项，采用平滑伪方法可以一定程度上降低交叉项的影响，但对简单信号的调幅特性反应失真，对实际工程信号某些能量较弱时段的时频分布更难以体现。经验模态分解(EMD)方法能将复杂工程信号分解成准单分量信号，可以借助相关系数法将分解过程产生的伪分量信号剔除，保证分解信号的有效性。通过EMD和WVD的结合，将分解后的准单分量信号进行WVD变换，进一步做平滑伪处理，从而获得复杂工程信号的时频分布特征。EMD～WVD的组合模型在仿真信号上应用效果良好，能够检测信号自身的时频特性，说明其理论基础的正确性，进一步将其应用在遥测振动信号上，同平滑伪WVD抑制交叉项方法进行了比较，结果表明该组合模型更加有效，能够反映复杂工程信号的时频分布特性，说明了其工程应用的可行性，研究结果对飞行器飞行试验结构和环境分析具有指导意义。

[1] Huang N E,Shen Z,Long S,et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[Z]. 1998.

[2] Huang N E,Shen Z,Long S.A new view of nonlinear water waves: The Hilbert spectrum[J]. Annu. Rev. Fluid Mech, 1999,31(1):417-457.

[3] Rilling G,Flandrin P,Gonc P, et al.On empirical mode decomposition and its algorithms[A].IEEE-EURASIP Work shop on Nonlinear Signal and Image Processing, NSIP-03[C]. 2003, 1-5.

[4] Huang N E,Wu M,Long S, et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proc. R. Soc. Lond. A, September, 2003, 459(2037): 2317-2345.

[5] 张贤达，保 铮．非平稳信号分析与处理[M].北京：国防工业出版社，1998.

[6] 钟佑明.希尔伯特-黄变换局瞬信号分析理论的研究[M].博士论文 2002.

[7] 李振兴，孟庆海.时频分析技术及其工程应用[M].大连：大连海事大学出版社，2011.

[8] 黄大吉，赵进平，苏纪兰.希尔伯特-黄变换的端点拖延[J].海洋学报，2003，25(1)：1-11.

[9] 李天云，赵 妍，季小慧，李楠.HHT方法在电力系统故障信号分析中的应用[J].电工技术学报,2005(6)：87-91.

[10] 沈国际，陶利民，陈仲生.多频信号经验模态分解的理论研究及应用[J].振动工程学报，2005，18(1)：994.

[11] 盖 强，张海勇，徐晓刚. Hilbert-Huang变换的自适应频率多分辨分析研究[J].电子学报, 2005(3):563-566.

[12] 陈军圣，于德介，杨 宇.希尔伯特-黄变换端点效应问题的探讨[J].振动与冲击，2005，24(6)：40-42.

[13] 赵 玲，刘小峰，秦树人等. 消除经验模态分解中混叠现象的改进掩膜信号法[J].振动与冲击，2010，29(9):13-17.

[14] 邹红星，戴琼海，李衍达等. 不含交叉扰项且具有WVD聚集性的时频分布之不存在性[J]. 中国科学，2001，3(4).

[15] 秦品乐，林 焰，陈 明．基于小波去噪和EMD的船舶液位信号特性分析[J]. 计算机工程，2008，34(18)：13-16.

[16] 蔡艳平，李艾华，李仁兵等.基于经验模态分解的WVD交叉项抑制法[J]. 计算机工程，2011，37(7)：271-273.

Use of EMD and WVD as Applied to Telemetry Vibration Signal

Wang Wanjin, Zhang Zhiguo, Xu Hongzhou

(PLA 91550 94 units, Dalian 116023, China)

Aircraft flight test telemetry vibration signal band gathered rich and complex composition, reasonable and effective interpretation information is crucial in the analysis of aircraft structure and its environmental characteristics include the frequency. Relying on empirical mode decomposition (EMD) method complex signal into quasi-single component signal, with the correlation coefficient pseudo component signal removed, ensure the validity of the decomposition of the signal. By combining EMD and WVD method, the quasi-single component of the signal remains were smoothed pseudo WVD transform and do treatment, thereby obtaining a complex signal frequency distribution. EMD-WVD combined model through the simulation test signal applications can be detected when the frequency characteristics of the signal itself. Its further application in the vibration signal telemetry, with smoothed pseudo WVD cross-term suppression methods are compared, the results show that EMD-WVD combination model more effective, when the project to reflect the complex - frequency distribution.

telemetry vibration signal; EMD, Wigner-Ville distribution; correlation coefficient

2015-09-21；

2016-03-07。

王万金(1982-)，男，辽宁人，理学硕士，工程师，主要从事信号处理及电磁拓扑技术方向的研究。

1671-4598(2016)07-0164-03

10.16526/j.cnki.11-4762/tp.2016.07.044

TH212；TH213.3

A