基于PID算法的四旋翼飞行器定点跟踪控制

李 希，陈 洋，陈鹏震

(武汉科技大学 信息科学与工程学院，武汉 430081)

基于PID算法的四旋翼飞行器定点跟踪控制

李 希，陈 洋，陈鹏震

(武汉科技大学 信息科学与工程学院，武汉 430081)

四旋翼飞行器是一种结构紧凑、飞行方式独特的垂直起降式飞行器，具有欠驱动、强耦合的特点；为实现对飞行器的控制，使之能从起始位置在一定时间内到达设定目标点并稳定悬停，根据其飞行特点建立动力学模型并在此基础上提出了一种双闭环PID控制方法；其中，外环实现飞行器的位置控制，使用目标点与反馈回的实际坐标的偏差作为控制器的输入，内环实现飞行器的姿态控制，其姿态的参考量由外环的输出经逆向求解获得的欧拉角与实际姿态角求得的偏差作为控制器的输入；通过PID算法后输出的姿态控制信号，经过四旋翼飞行器“十”字动力学模型解耦得到4个电机的转速控制值，从而完成定点跟踪任务；提出的双闭环PID控制方法在仿真中获得了验证，为飞行器的进一步研究提供了基础。

四旋翼飞行器；动力学模型；双闭环；PID控制器；定点跟踪

0 引言

随着计算机技术和自动化技术的不断发展，旋翼式飞行器技术在越来越多的领域有广阔的应用前景，四旋翼飞行器是一种结构紧凑、飞行方式独特的垂直起降式飞行器，具有欠驱动、强耦合的特点，通过调节对称分布的四个旋翼转速，实现对飞行姿态的控制。由于它具有普通无人机没有的优势，如垂直起降、协调转弯、空中悬停、侧飞、前飞等多种飞行模态，这决定了它在军用方面可以应用于进行侦查、攻击、通信、监视等工作，在民用方面可以应用于航拍、交通监控、大气检测、电力巡检、除冰等工作[1]。

目前，对于四旋翼飞行器的控制系统设计，国内外众多高校和科研机构进行了相关方面的研究，目前较为常用的控制算法有：PID控制器[2]，自抗扰控制器(ADRC)，线性二次型最优调节控制器(LQR)，滑模控制算法(Sliding-mode)，BackStepping控制算法。自抗扰控制器针对动力学模型中的未建模项，在传统的PID控制器中加入不确定函数和外界干扰，增强了机体的鲁棒性[3]，由于加入了外界未知干扰导致控制精度不够。线性二次型最优调节控制器通过构造线性二次型问题的状态方程，求解不同拉力下各个电机角度以及角速度[4]，该方法能缩短机体的响应时间，但是需要建立电机模型，过程复杂，使得控制系统的实时性不足；本文将采用经典的PID控制器，通过设计双环结构来实现对四旋翼飞行器的跟踪控制。该方法在四旋翼动力学模型的基础上设计了位置控制器和姿态控制器，能较好的控制机体的姿态角和移动速度，通过设置合适的参数也能克服跟踪精度不高的缺点。

本文运用Newton-Euler公式建立简化的四旋翼飞行器动力学模型[5-6]，并进行简化，运用PID算法，通过建立位置环、姿态环双闭环控制系统，实现了对四旋翼飞行器各通道控制律的设计，并在实验室模型样机上通过Simulink仿真实验，实现了四旋翼飞行器精确、稳定的定点飞行和稳定悬停，论证了算法的实时性、准确性。

1 动力学模型

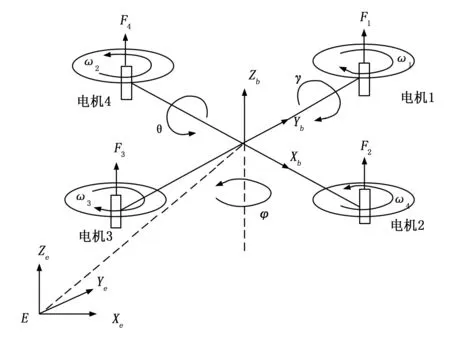
图1 四旋翼飞行器动力学建模示意图

1.1 平移动力学模型

为得到飞行器在机体坐标系中的受力FB与在导航系中受力FE的关系，假设机体按照先Z轴，Y轴，再X轴的顺序转动，这3次转动可表示为3个独立方向余弦矩阵。

则在此种转动顺序下，可定义：

从E系到B系的方向余弦矩阵：

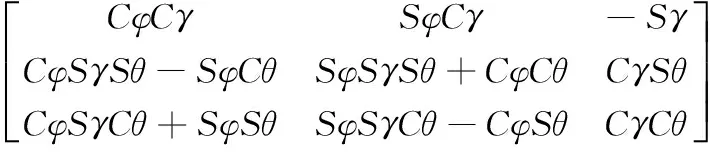
式中，Cφ=cosφ,Sφ=sinφ，同下。

从B系到E的方向余弦矩阵为：

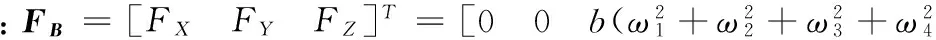
在导航系中机体的升力为：

(1)

(2)

1.2 转动动力学模型

四旋翼飞行器在飞行过程中，若忽略空气阻力和旋翼的陀螺效应，则飞行器在机体系中的转动力矩为：

(3)

式(3)中，Jx、Jy、Jz分别为机体绕机体坐标系xb,yb,zb轴转动的转动惯量；假设旋翼质心到机体质心的距离为l；p、q、r分别为机体绕机体坐标系B的xb,yb,zb轴转动角速度。

根据上图，可推得QE与QB的关系：

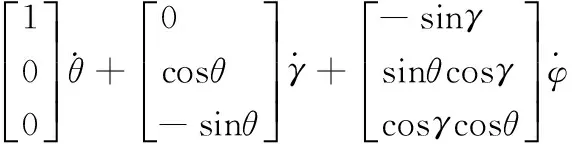
(4)

飞行器在悬停或者是匀速运动时，可以认为机体的欧拉角变化很小，接近0度，将θ=0,γ=0,φ=0代入公式(4)，得：

(5)

式(5)表明，机体在机体系中的角速度等于欧拉角的角速度，而转动力矩为:

(6)

式(6)表明，转动力矩M与角速度ω的导数成正比，而E系中的转动惯量J与B系中的转动惯量J相同，所以:

(7)

由公式(6)和公式(7)可得转动动力学模型：

(8)

通过改变飞行器电机转速，可以实现各种不同的运动。可将其合运动分解到四个独立方向，分别为：

1)上下运动(控制律U1)。

实现方法：四个电机转速一致，四个旋翼产生的升力大于或小于自身重力。

2)前后运动和俯仰角θ(控制律U2)。

实现方法：电机2、4转速不变，电机1，3转速一增一减且改变值相同。

3)左右运动和横滚角γ(控制律U3)。

实现方法：电机1、3转速不变，电机2、4转速一增一减且改变值相同。

4)偏航运动和偏航角φ(控制律U4)。

实现方法：电机1、3为一组，电机2、4为一组，一增一减且改变值相同，机体的旋转方向与转速快的旋翼的旋转方向相反。

注意：上下、前后、左右运动需抵消机身的反扭矩，使机身保持平衡，所以改变电机转速实现这几种运动的前提条件是τ1+τ3=τ2+τ4，即ω12+ ω32= ω22+ ω42。

假设1电机朝前为正方向，2电机朝右为正方向，电机1、3的旋转方向为偏航角的正方向，则每个通道的控制律如下：

(9)

将公式(9)代入公式(2)和公式(8)中即可得到简化的动力学模型，如式(10)所示。

(10)

2 控制器的设计

根据以上动力学模型的分析可知，可以通过改变四个电机的转速来控制飞行器的运动状态，机体在空间的移动速度主要是通过改变相应姿态角的大小来控制的，所以为实现飞行器定点跟踪，关键在于得到准确的姿态控制信号，控制器的设计如图2所示。

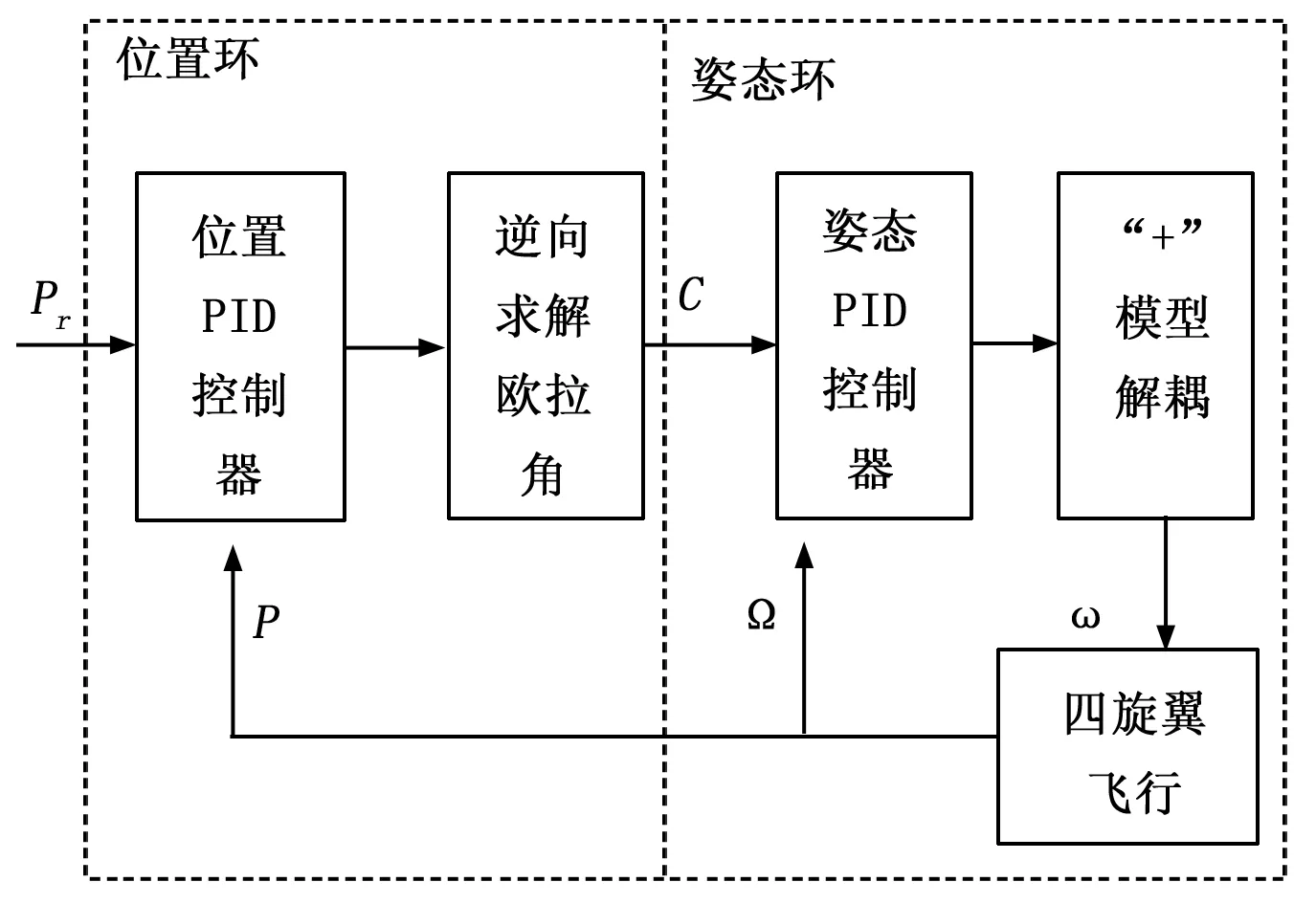
图2 控制结构示意图

从图2中可看出，该控制器采用双闭环控制结构，姿态控制作为内环，位置控制为外环，内环的设定值由外环的输出值通过逆向求解欧拉角得来。输出的姿态控制信号通过“十”模型解耦得到4个电机的转速从而控制飞行器的运动状态。

(11)

外环位置PID控制器的输出作为逆向求解欧拉角模块的输入。飞行器在定点跟踪的运动过程中，可以仅依靠上下、左右、前后运动就可完成在空间中从一点到另一点的飞行任务，所以，为了控制的方便，不妨假设偏航角φ=0，代入平移动力学模型公式(11)中可得：

(12)

由公式(12)可解得：

而φr=0

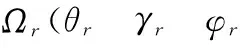
(13)

根据控制律公式(9)及其实现方法，可得到：

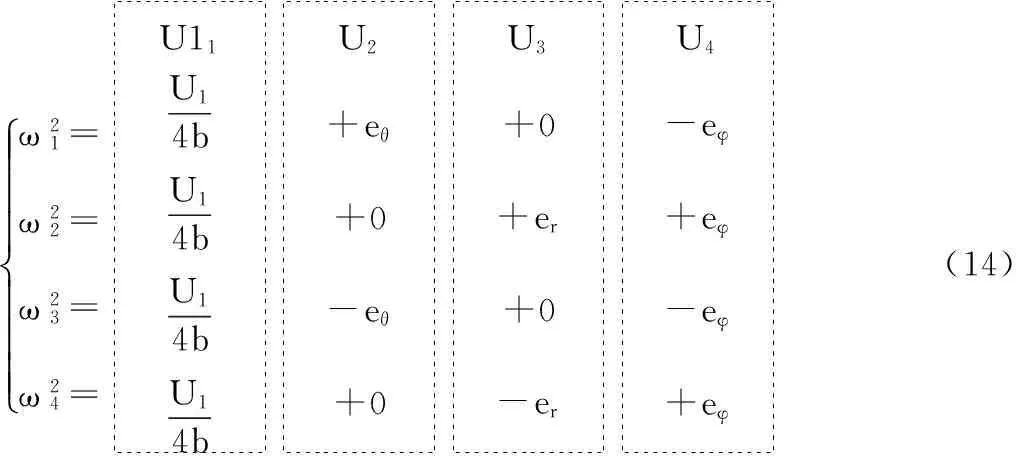
U11U2U3U4 ω21=ω22=ω23=ω24=ìîíïïïïïïU14bU14bU14bU14b+eθ+0-eθ+0+0+er+0-er-eφ+eφ-eφ+eφ(14)

利用公式(14)即可用3个姿态控制信号得到4个电机的转速控制信号，这就是“十”字模型解耦。

然后将转速控制信号相应地转换成各个电机的PWM波的占空比，使电机输出转速，从而使飞行器能在规定时间内完成定点跟踪任务。

3 实验结果与分析

用Matlab的Simulink模块搭建上述四旋翼飞行器动力学模型及其控制器，通过仿真结果验证此方法的可行性。其中飞行器参数暂定为：

b=2.289 3×10-5N·s2

d=1.189 7×10-6N·s2

m=2.467 kg

l=0.387 5 m

Jx=0.058 87 kg·s2

Jy=0.058 87 kg·s2

Jz=0.131 51 kg·s2

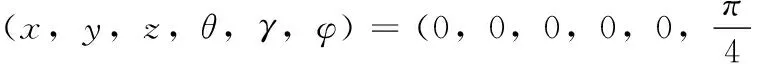
由图3和图4可以看出四旋翼飞行器在4s左右能够很快的到达设定目标点并能够稳定悬停，图5为飞行器的三维飞行轨迹图，由此可以看出通过设计出的双闭环PID控制器来控制飞行器完成指定飞行任务是可行的。

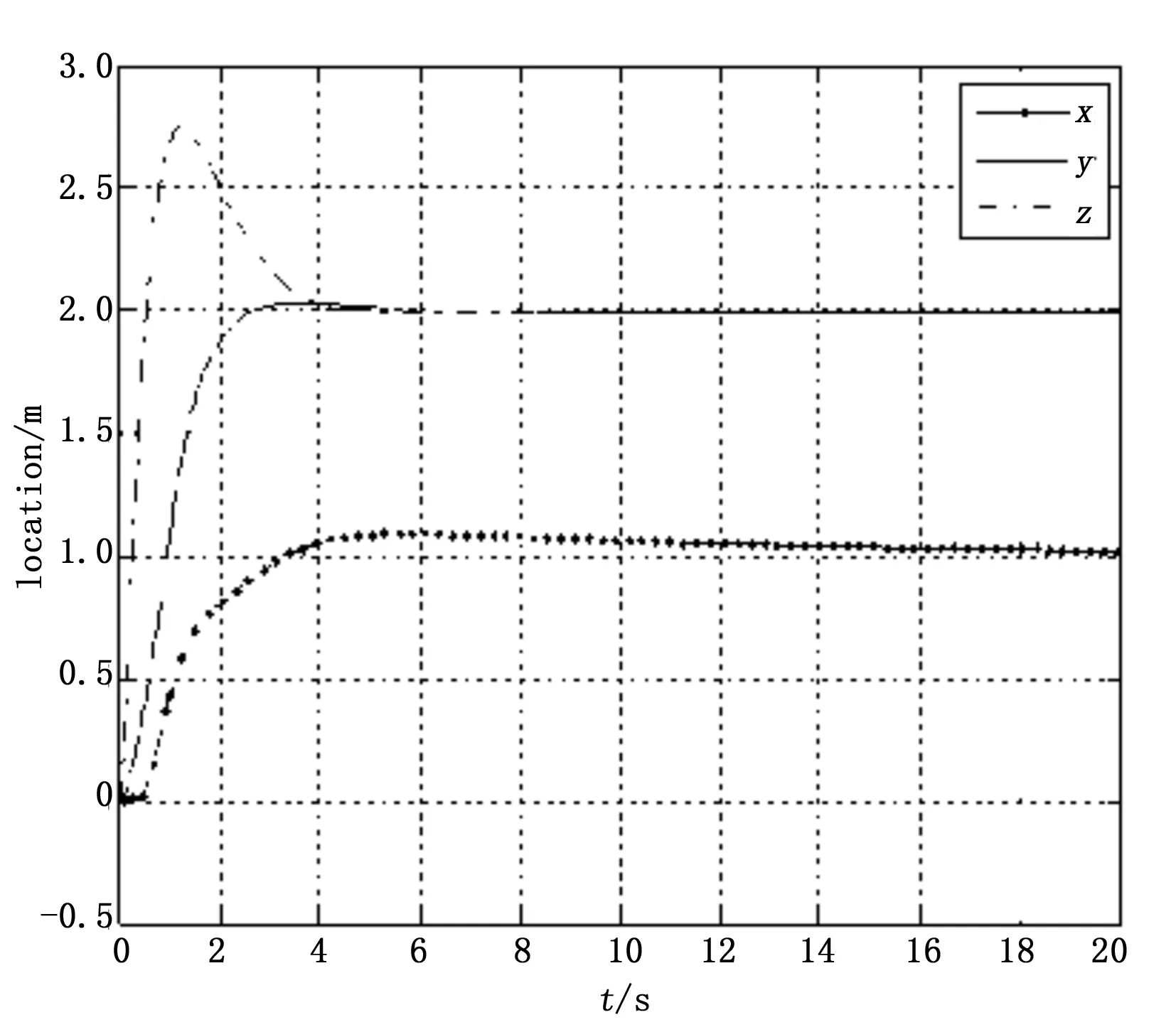
图3 四旋翼飞行器飞行位置坐标曲线

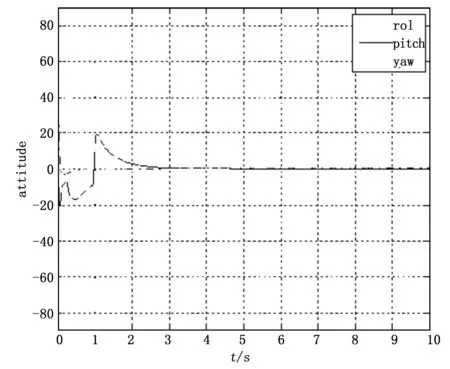
图4 四旋翼飞行器飞行姿态曲线

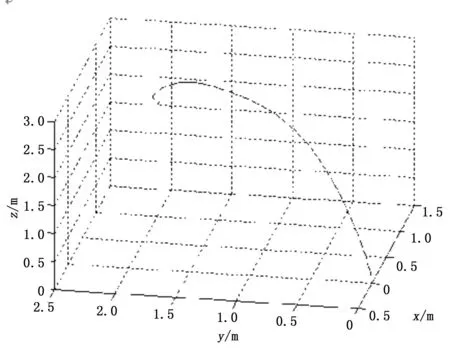
图5 四旋翼飞行器三维飞行轨迹曲线

4 结论

本文通过对飞行器各部分的运动机理进行分析，依据其所遵循的基本规律得到动力学模型，并在此基础上对飞行器的定点跟踪任务进行分析，提出由外环位置环和内环姿态环构成的双闭环PID控制系统，并通过仿真验证了该系统的可行性。本文重点在于对飞行器建模和双闭环 PID控制器的分析，对于通过GPS、气压计检测出飞行器的实际坐标位置的方法以及姿态解算算法(比如四元数算法)并未做详细分析。另外，对于PID算法中比例、积分、微分调节系数KP、KI、KD的整定是根据飞行器的实际情况和以上的理论分析利用试凑法来实现的。

但是，从图5的三维飞行轨迹图来看双闭环PID控制系统并不能控制飞行器沿最优的路径飞行——直线，并且其飞行路径无法确定，完全是由控制算法控制其飞向目标，所以路径规划是很有必要的，这也将是下一步努力的方向。

[1] 聂博文, 马宏绪, 王 剑，等. 微小型四旋翼飞行器的研究现状与关键技术[J].电光与控制，2007(6)：113-117.

[2] 吴成富, 刘小齐, 袁 旭. 四旋翼无人机建模及其PID控制律设计[J].电子设计工程，2012，16：68-70.

[3] 齐晓慧, 王洪军. 四旋翼无人机的自抗扰控制研究[J]. 测控技术，2014(5)：61-64.

[4] 丛梦苑. 基于线性二次调节器的四旋翼飞行器控制系统的设计与研究[D]. 哈尔滨：哈尔滨工程大学，2011.

[5] 赵育善, 师 鹏. 航天器飞行动力学建模理论与方法[M]. 北京：北京航空航天大学出版社，2012.

[6] 聂博文. 微小型四旋翼无人直升机建模及控制方法研究[D]. 长沙：国防科学技术大学，2006.

[7] Alexis K, Nikolakopoulos G, Tzes A. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances[J]. Control Engineering Practice, 2011, 19(10): 1195-1207.

[8] Xu R, Ozguner U. Sliding Mode Control of a Quadrotor Helicopter[A]. IEEE Conference on Decision and Control[C]. 2006:4957-4962.

[9] Hoffman G M, Huang H M, Waslander S L, et al. Precision flight control for a multi-vehicle quadrotor helicopter testbed[J]. Control Engineering Practice, 2011,19(9): 1023-1036.

[10] Wang J, Huang Y Ma L. Extending the Player Project for flexible cooperation of multiple robots[A]. International Conference on Mechatronics and Automation(ICMA)[C]. 2012: 1657-1662.

Quadrotor Tracking Control Based on PID Algorithm

Li Xi，Chen Yang，Chen Pengzhen

(College of information science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)

Quadrotor is a way to VTOL aircraft that has compact structure and unique fight, with underactuated and strong coupling characteristics. For controlling the aircraft to arrive at set-point and maintains a stable hover from initial location, the article proposed the method of double close-loop PID control based on the dynamic model according to its flight characteristics, the outer ring accomplishes location control,we set the error between set-point and feedback actual location as the controller. the inner ring accomplishes attitude control, the set-value of the attitude results form the inverse solution of outer ring’s output, that the error between the set-value and actual attitude is the input of controller .after double close-loop PID, the signals for controlling attitude will be output, which can convert to four value used to control motor speed via the decoupling of cross dynamic model of quadrotor. The task of set-point tracking can be accomplished according to above all. the method of double close-loop PID control in this article can be verified with simulation experiments, providing a basis for furture study on the quadrotor.

quadrotor; dynamic model; double close-loop; PID control; set- point tracking

2016-01-13；

2016-03-07。

国家自然科学基金项目(62103331, 61573263)；湖北省科技支撑计划项目(2015BAA018)。

李 希(1994-)，女，湖北咸宁人，主要从事旋翼飞行器自主控制方向的研究 。

1671-4598(2016)07-0109-04

10.16526/j.cnki.11-4762/tp.2016.07.029

TP301.6 文献标识码：A