基于神经网络模糊控制理论的转台伺服系统控制设计
2016-10-28路平,刘凯,王龙
路 平,刘 凯,王 龙
(1.军械工程学院 无人机工程系,石家庄 050003;2.中国人民解放军93420部队,石家庄 050071)
基于神经网络模糊控制理论的转台伺服系统控制设计
路 平1,刘 凯2,王 龙1
(1.军械工程学院 无人机工程系,石家庄 050003;2.中国人民解放军93420部队,石家庄 050071)
针对三轴飞行仿真转台伺服系统非线性、模型不精确等特点,在分析转台系统结构的基础上,采用模糊PID控制的方法对转台伺服系统进行仿真控制,得到较好的控制效果;模糊控制控制规则的获得带有很大的人为因素,并且在控制过程中对规则采用查表法占用大量的内存;基于以上原因,设计了神经网络模糊控制器(NNSOC),利用神经网络控制自学习、自调整的能力,为模糊控制器提供自动生成控制规则的能力;同时由于神经网络具有联系记忆能力,可对未训练的样本做出决策;对NNSOC的控制效果进行了仿真;结果表明:其具有很好的动态性能和鲁棒性,对转台的控制效果良好。
模糊控制;神经网络;神经网络模糊控制;转台;直流无刷电机
0 引言
三轴飞行仿真转台是一种三轴自动框架式多功能半实物仿真测试设备。它可以按照实验要求,提供飞行器飞行时的航向角、俯仰角、横滚角及飞行扰动,实时模拟飞行器在空中飞行的姿态。对转台伺服系统的高精度控制是实现转台功能的核心要求。这就需要一种合理的控制算法。
当前,对于转台伺服系统的控制多采用常规PID控制、模糊PID控制、神经网络PID控制、自适应控制等。文献[1]论述了常规PID的控制方法,对线性系统具有很好的控制效果,但对于实际伺服系统来说,由于存在非线性和参数时变性,很难达到理想的控制效果;文献[2-3]提出,模糊控制对于数学模型的依赖程度不高,系统鲁棒性强,适用于非线性时变系统的控制,采用模糊PID控制方法实现了对伺服系统的有效控制;文献[4]针对仿真转台不易建立精确数学且要求控制结构简单而实用的特点,提出了带比例因子的模糊自适应PID的伺服系统控制方法。
以上文献证明了模糊PID及其改进算法能够对转台伺服系统实施较好的控制。然而模糊控制的控制效果取决于是否正确、全面和有效地将操作人员的控制经验总结为一系列语言控制规则。在某些系统中,由于设计者和操作人员经验的局限性,总成模糊控制器无法保证最优或次优的控制性能。文献[5]设计了一种基于神经网络的自组织模糊控制器(NNSOC),将神经网络与模糊控制结合,为模糊控制器提供了良好的学习功能,并自动生成模糊控制规则,兼备两种技术的优点。
本文首先分析了转台伺服系统的数学模型;而后应用神经网络模糊控制的方法,对转台伺服系统神经网络模糊控制器进行了设计;最后,通过MATLAB仿真,验证了神经网络模糊控制器对转台伺服系统能够进行准确、有效地控制。
1 转台伺服系统的数学模型
本课题采用直流无刷电机作为伺服系统的驱动电机,其主要功能是是驱动转台各框架按照设定要求进行偏转,准确模拟飞行器在空中的飞行姿态。
飞行仿真转台采用典型的双闭环控制系统,其结构如图1所示。
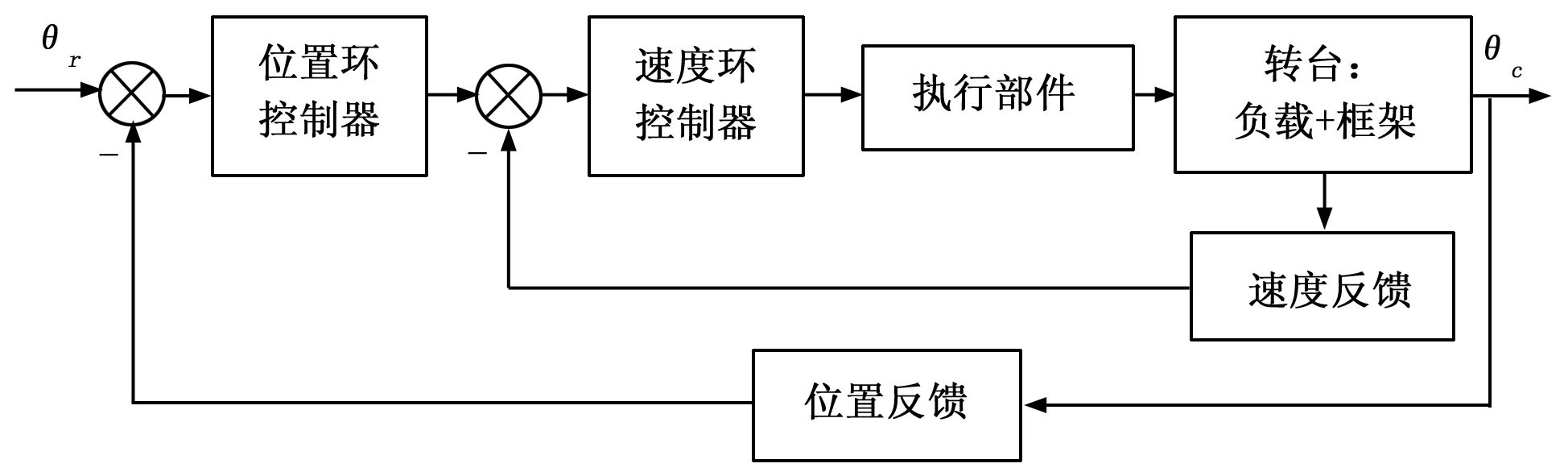
图1 转台系统结构框图
三轴飞行仿真转台由功率放大器、直流无刷电机(执行部件)、台体(负载+框架)以及光电编码器(位置测量元件)组成。
忽略机械轴上的弹性形变和弯曲,将直流无刷电机和负载视为一个刚体,即单质量伺服系统来考虑。
根据文献[6],直流无刷电机满足的数学模型为:
(1)
式(1)中,Tm=GD2R/375CeCm为电力拖动系统时间常数;Ce=E/n为电动势常数;Cm=300 Ce/π为电动机额定励磁下的转矩电流比;R、L为电枢回路总电阻和总电感;Tl=L/R为电枢回路电磁时间常数。
由n=60 ω/2π得:
(2)
式(2)中,Te为额定励磁下的电磁转矩;TL为包括电机空载转矩在内的负载转矩。
由动力学关系式:
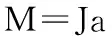
(3)
可知式(3)中,30 GD2/375 π为直流无刷电机转轴上的转动惯量,它由电机本身的转动惯量和转台各框架折合到电机转轴上的转动惯量组成。
以三轴转台中的偏航转台为例,根据转台伺服电机的具体参数结构,建立系统的近似数学模型为:
(4)
2 神经网络模糊控制器 [7]
2.1 转台伺服系统的模糊控制策略
飞行仿真转台模糊控制系统包括PID控制器、模糊控制器、转台伺服系统、位置反馈系统等四部分。模糊控制器对PID控制器的控制参数进行自适应调整,PID控制器的输出为系统实际控制量。其结构如图2所示。图中r(t)为转台伺服系统的输入(指定位置信号),y(t)为转台框架的实际转动角度。

图2 模糊控制结构图
模糊PID控制器的离散形似可表示为:
(5)
(6)
(7)
(8)
将系统误差e(t)和误差变化率ec(t)进行模糊化和归一化处理。误差E、误差变化率EC和PID3个参数的修正值对应的模糊集各分为七档,即{负大,负中,负小,零,正小,正中,正大}={NB,NM,NS,ZO,PS,PM,PB}。
E,EC和ΔKP、ΔKI和ΔKD的论域均为:{-6,-4,……,4,6}。
隶属度函数均为三角形,如图3所示。

图3 隶属度函数图
根据文献[8]和文献[9]说明的PID参数整定原则以及工程技术人员的技术知识和实际操作经验,建立模糊控制规则表为:
依据表1所示的模糊控制规则,建立模糊PID控制的仿真模型,对模糊PID控制器的控制效果进行阶跃响应仿真分析,仿真结果如图4所示。
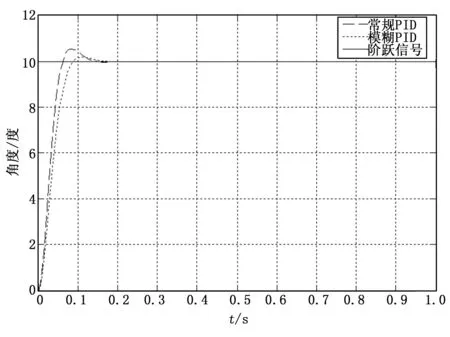
图4 模糊PID仿真结果图
2.2 神经网络模糊控制器简介[10]
根据模糊控制仿真图可知,模糊PID控制器的控制效果良好,达到了转台的控制要求。
然而,模糊PID控制器的控制效果很大程度上取决于工程操作人员的实际经验。同时,一般的模糊控制器将“专家经验”通过模糊规则体现出来,在系统运行中,通过查表等方式做出决策,输出控制量。这样就会占用大量的内存空间,并且查表反应速度较慢,使得转台控制的实时性能力下降。
将神经网络引入到模糊控制中,利用神经网络的自学习、自调整能力,对样本进行训练,使其记忆模糊控制规则。控制的反应速度快,对于未训练的样本,可以通过联想记忆功能做出决策,表现灵活。
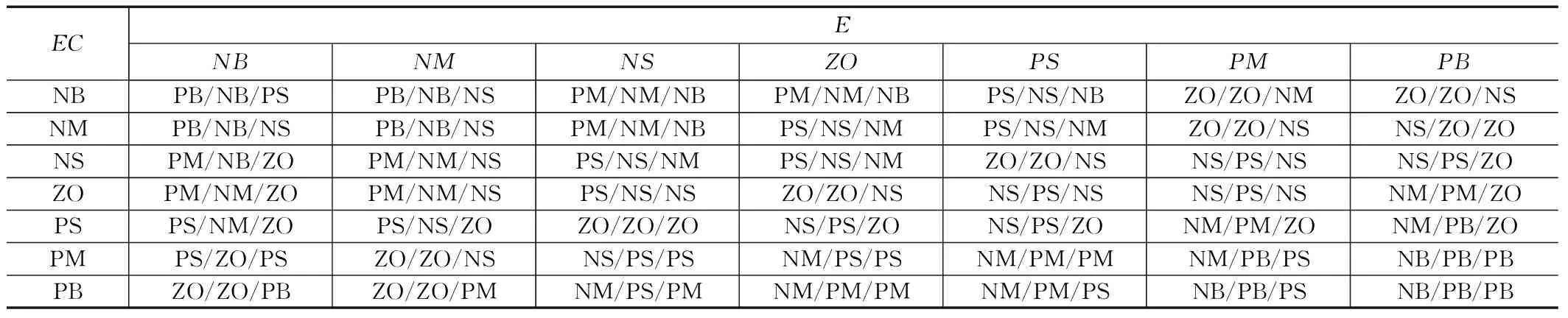
表1 模糊控制规则表
基于神经网络的自组织模糊控制器(NNSOC)的系统结构如图5所示[9]。其控制规则通过一个神经网络执行,由BP学习算法实现。
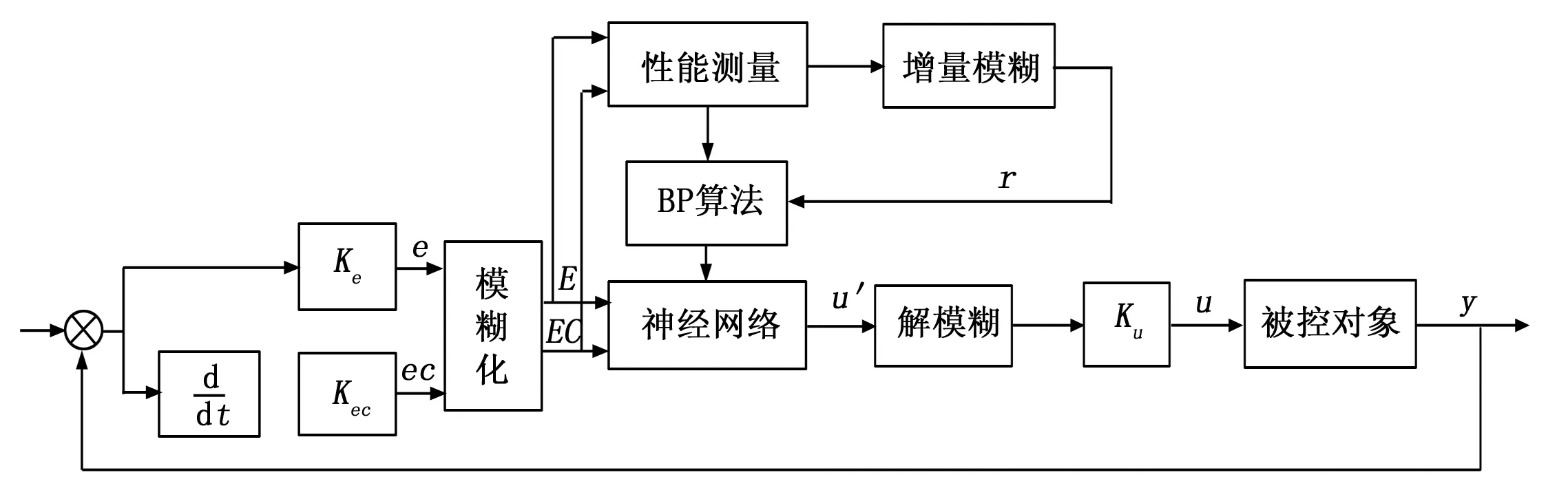
图5 NNSOC系统结构图
NNSOC主要由以下三部分组成:
(1)控制器。NNSOC中的控制器是由神经网络实现的,网络的输出代表了一个真实的控制量,而不是一个模糊子集,因而无需了解模糊过程。
(2)性能测量部分。用来对控制器自身作用进行评估。
(3)控制器自校正部分。在NNSOC中,采用BP算法进行一定次数的反复计算,通过调整神经网络的权值来修正控制量,实现期望的控制效果。
2.3 转台的神经网络模糊控制器设计
如图6所示,为转台伺服系统的神经网络模糊控制器结构图。

图6 转台伺服系统NNSOC结构图
神经网络结构图如图7所示。
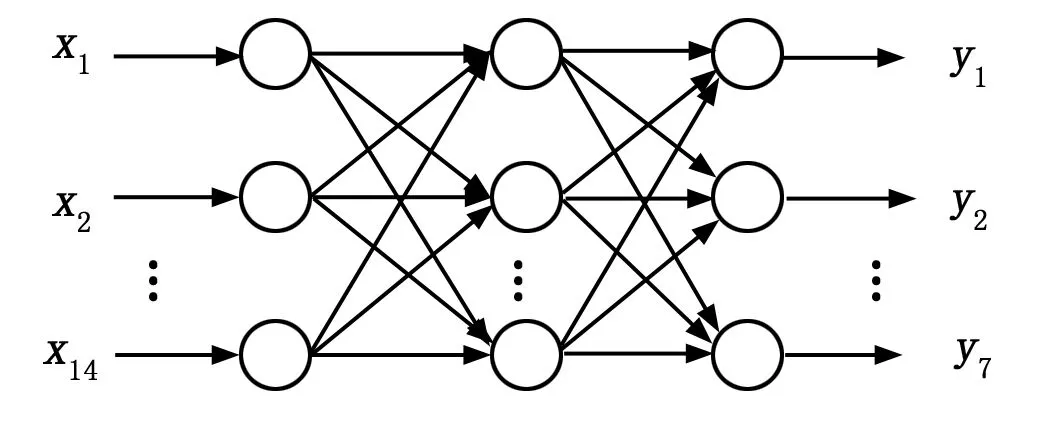
图7 神经网络结构图
网络的输入空间对应转台位置(偏转角度)误差和误差变化率两个变量。根据上文对模糊子集的分类,每个输入变量都有7个输入单元与其7个模糊子集相对应。
网络的输入信号格式为:
网络的每一个输入单元都对应着输出变量空间中的一个量化值。因此,输出的模糊子集就可以量化空间上的隶属函数来表示。输出信号的格式为:
神经网络模糊控制器采用一个单隐层的BP网络。根据上文论述,网络的输入值为误差E和误差变化率EC对于某一个模糊变量A的隶属度。
以E=NS,EC=PM为例。它的输入层为14个,其中x1~x7代表e(t)的模糊子集,x8~x14代表ec(t)的模糊子集。网络的输入信号为:
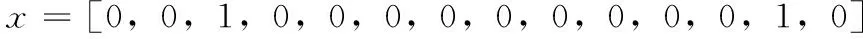
网络的输出层为21个,其中y1~y7代表ΔKP的模糊子集;y8~y14代表ΔKI的模糊子集;y15~y21代表ΔKD的模糊子集。根据模糊规则控制表可知ΔKP=NS、ΔKI=PS、ΔKD=PS此时则网络的输出信号为:
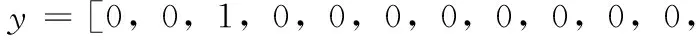
1,0,0,0,0,0,0,1,0,0]
x和y中的各元素为对应的隶属函数,即模糊子集的赋值。依据上述方法,可以列出7×7=49个样本对。将样本对送入神经网络进行离线训练,训练结束后,神经网络已经记忆了模糊控制规则,使用时具有联想记忆功能。
3 系统仿真
3.1 样本训练
根据表1确立的模糊规则,建立神经网络的训练样本。其训练样本形式为:
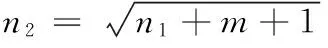
由于输入层有14个结点,输出层有21个结点,所以BP神经网络的隐含层结点数选为15个。
隐含层神经网络的传递函数为tansig;输出层神经元传递函数为logsig;网络训练函数为traingdx。
根据以上设定信息对49个样本对进行训练,得到的训练结果如图8所示。
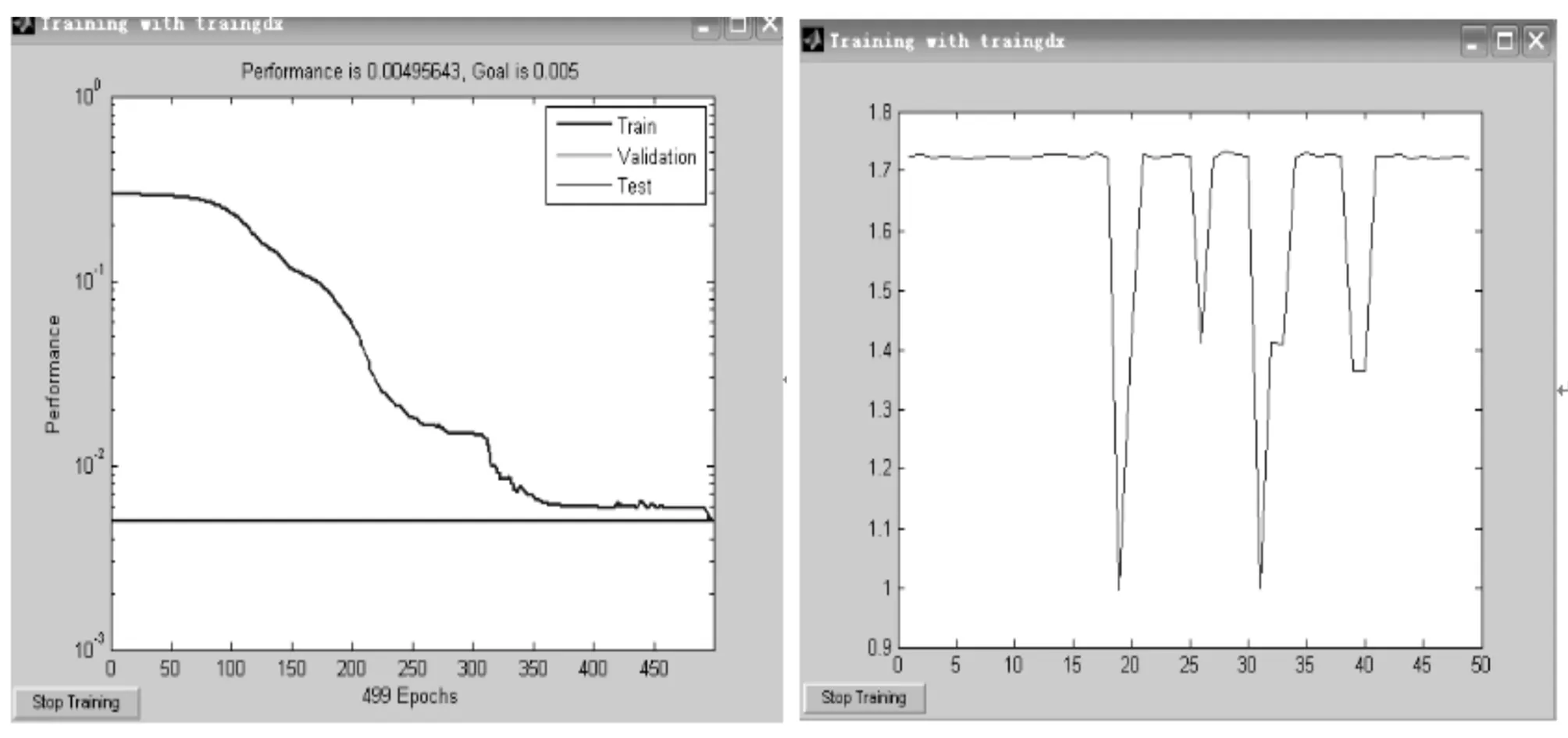
图8 样本训练结果图
由图8可知。网络训练499次后,训练目标误差减小到0.005以下,各个样本误差均小于2%,达到训练要求。
3.2 控制器性能仿真分析
将样本送入神经网络进行离线训练以后,训练好的神经网络已经记忆了转台伺服系统的模糊控制规则,相当于一个模糊关系存储器。
将转台位置误差和误差变化率的实际值模糊化后输入网络,得到的网络输出信号经过解模糊,得到PID控制器的修正值。
对神经网络模糊控制器的控制效果进行仿真,仿真结果如图9所示。
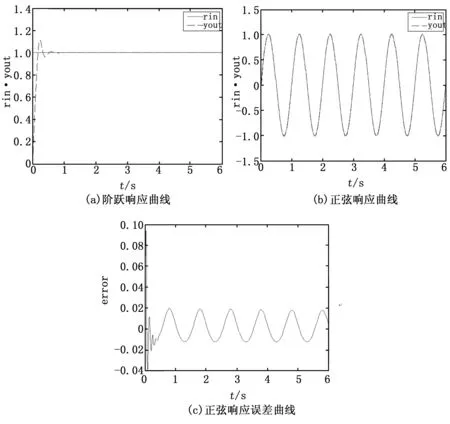
图9 基于NNSOC的PID控制曲线
由图9(a)可知,本文提出的神经网络模糊控制器对于阶跃响应的响应时间为0.18 s,超调量为0.15。在响应时间和鲁棒性方面性能较好。
由图9(b)和9(c)知,神经网络模糊控制对正弦信号有很好的跟踪能力。其跟踪误差为2%。可见,神经网络模糊控制器的动态性能良好。
4 结论
本文针对三轴飞行仿真转台伺服系统,在常规模糊PID控制器的基础上引入神经网络,设计了神经网络模糊控制器。
根据仿真实验的结果看出,该控制器的设计很好的满足了对转台伺服系统动态性能和鲁棒性的要求。同时,对于样本的训练采用离线的方式进行,可以满足转台控制的实时性要求。
[1] 石文兵,唐小琦.基于模糊自整定PID的二质量伺服控制系统的研究[J].工业仪表与自动化装置,2007 (2):3-5.
[2] 凡永华,岳小飞,于云峰,等.基于模糊控制的高空姿态控制系统设计[J].测控技术,2011,30(12):45-48.
[3] 吴艳敏,崔光照,黄 春,等.模糊自适应PID在转台位置控制中的应用[J].机床与液压,2009,37(3):127-129.
[4] 吕 博,吴云洁.基于模糊自适应PID的伺服系统控制[J].系统仿真学报,2009,21(21):6794-6797.
[5] 王丽珍.神经网络自组织模糊控制算法及其应用[J]. 机械研究与应用,2011(6):10-12.
[6] 甄红涛,齐晓慧.智能车参数自校正方向模糊控制器的设计[J].自动化仪表,2010,31(9):57-59.
[7] 付 强.一种基于RBF神经网络的转台分系统故障诊断方法[J].传感器与微系统,2007,26(6):26-32.
[8] 陈志佳,孙书鹰,张炜栋.三相直流电机伺服系统设计[J].自动化仪表,2012,33(1):44-47.
[9] 王祥好.模糊PID控制算法在智能小车中的研究与应用[D].合肥:合肥工业大学,2009.
[10] 顾 晨,赵国军,刘 峥.基于人工神经网络的自适应模糊电梯群控系统[J].计算机测量与控制,2003,11(12):947-949,939,961.
[11] 张德丰.MATLAB神经网络编程[M].北京:化学工业出版社,2011.
[12] 王发智,曹建鹰,牛润勋.基于神经网络的热风炉的模糊控制[J].化工自动化及仪表,2012,37(1):14-18.
Control of Turntable Servo System Based on NNSOC Method
Lu Ping1,Liu Kai2,Wang Long1
(Department of Optics and Electronics Engineering ,Ordnance Engineering College, Shijiazhuang 050003,China)
The three-axis turntable is nonlinear and the model is not precise. The paper analyses the structure of the turntable and adapts Fuzzy PID control method to control the turntable servo system. Also, make some simulation and result shows that the effect of Fuzzy PID is good. However, the rules of Fuzzy PID controller get from the experience of technician and take too much memory space. For these reasons, the paper designs a Neural Network (NN) Self-organizing Controller (NNSOC). Using the self-study and self-adjust ability of Neural Network, NNSOC provides control rules to Fuzzy PID controller. Meanwhile, because of the memory ability of NN, NNSOC can make decisions to the untrained samples. Make some simulation on NNSOC. Results show that NNSOC has good abilities of and robustness, the effect of controlling on turntable servo system is good.
fuzzy control; neural network; NNSOC; turntable; brushless DC motor
2015-10-22;
2016-01-29。
路 平(1961-),男,河北石家庄人,教授,硕士研究生导师,主要从事无人机通信链路与导航方向的研究。
1671-4598(2016)07-0086-04
10.16526/j.cnki.11-4762/tp.2016.07.023
TP13 文献标识码:A
