基于机器视觉的高精度测量与装配系统设计
2016-10-28胡国清吕成志赵朋飞
焦 亮,胡国清,吕成志,赵朋飞
(华南理工大学 机械与汽车工程学院,广州 510640)
基于机器视觉的高精度测量与装配系统设计
焦 亮,胡国清,吕成志,赵朋飞
(华南理工大学 机械与汽车工程学院,广州 510640)
在对某些精密产品实现自动化生产过程中,存在难以对装配该产品所需的多种装配小零件进行高精度自动测量与装配的问题;针对该问题,搭建了基于机器视觉技术的自动化测量与装配系统;基于Halcon图像处理软件平台,对零件图像进行了中值滤波、图像增强等预处理;采用了Canny算法对零件求取像素精度的边缘,并运用椭圆曲线拟合法获取了亚像素精度边缘;建立了两种相机镜头畸变模型,采用径向排列约束(RAC)标定法与张正友标定法对相机进行了标定,并对标定精度进行了对比;实验结果表明:本系统的装配同轴度精度能达到0.05mm,零件尺寸测量标准差低于3.8μm,满足工业需求,可以解决工业实际问题。
机器视觉;自动化装配;亚像素精度;畸变模型;相机标定
0 引言
随着工业自动化的发展,机器视觉广泛应用于工业领域,主要集中在电子行业、半导体行业、航天、测量等行业。机器视觉作为工业机器人获得外界环境信息的主要手段,可以提高工业生产的柔性与自动化程度,这使得对多种小零件的高精度测量与装配工作实现全自动化生产装配成为可能,可以提高装配效率,一般小零件的高精度装配对环境洁净度要求较高,实现自动化生产装配后,有利于对装配环境的保持与维护,减少了对装配环境维持的成本,提高了工业生产的稳定性与合格率。
机器视觉具有高效率和针对性强两大特点,面对各类工业需求,运用机器视觉技术开发相应的设备与解决方案,并取得了较理想的效果,王冠英等人采用线阵CCD扫描仪与Matlab图像处理技术相结合的方法,对织针针坯模具进行快速、准确地非接触测量,并取得了3 μm的测量精度[1];查英等人运用机器视觉技术构建了针对工业装配生产线的削刀架自动装配问题的在线视觉系统,取得了100%的识别零件正确率[2];李钊宝等人运用基于转轴法的外切矩形法对工件进行定位,并通过双线性差值算法实现工件边缘的亚像素提取,最终实现了0.015 mm的测量重复性精度[3];郭瑞等人设计了视觉系统到机器人的坐标标定及坐标值计算,实现了视觉系统对机器人精确定位的引导[4]。
针对某些精密产品自动化生产过程中,需对组成产品的多种小零件进行高精度测量和自动化装配问题,本文采用Keyence的CCD工业相机,运用光学测量理论、图像处理技术以及视觉定位算法来实现零件尺寸的高精度测量与自动化装配。首先对获取的零件图像进行预处理,减小噪声对图像的干扰,然后采用Canny算法提取像素精度边缘,在此基础上,通过椭圆曲线拟合法提取亚像素精度边缘,提高零件关键信息与尺寸的测量精度,满足工业需求。
1 系统总体方案设计
本文具体针对的问题:8种不同种类、不同尺寸圆形小零件需按要求依次叠放,且保证装配好的各类零件的中心与底座中心同轴度精度高于0.05 mm,同时测量每种零件的外径尺寸,精度高于0.01 mm。图1表示整个装配过程的流程。

图1 零件装配流程图
2 视觉系统设计
2.1 预处理
在进行图像采集过程中,不可避免地受到各种干扰而混入加性噪声,故需对图像进行滤波处理,图2(a)为8种装配小零件之一的圆片1原始灰度图,这里仅以该零件为例,需要获取的特征信息包括圆片1的外圆直径以及中心坐标值。
在圆片上存在若干白点噪声干扰,本文选用中值滤波算法对图像进行滤波,中值滤波是一种非线性滤波算法,能够在滤除随机噪声的同时,很好的保持图像的边缘信息[5]。
滤波后,通过图像增强使模糊的图像变清晰,图像增强算法可用式(1)所示。
(1)
其中:Yij为图像增强后序列,fij为增强前图像序列,a为比例系数,这个系数主要通过反复实验调试得到,本文取为2。
在图2为原始灰度图经过中值滤波,再经过图像增强处理的效果图,从图中可以看出,原始图像上的若干白点噪声基本被滤除。

图2 预处理效果图
2.2 亚像素边缘提取
图像边缘检测的目的是提取图像中物体的边缘,边缘提取效果的好坏直接影响到物体尺寸及定位信息的获取。边缘检测是图像测量的基础和关键,随着人们对检测精度要求的不断提高,像素级检测精度已经不能满足实际测量的要求,本文首先采用Canny算法提取像素级边缘,再采用椭圆曲线拟合法进一步求取亚像素精度边缘。
2.2.1 Canny算法
Canny算法具有良好的信噪比和检测精度,在图像处理领域应用广泛。检测时主要分为以下几个步骤:
1)采用高斯滤波进行图像去噪;2)计算梯度幅值和梯度方向;3)非极大值抑制;4)双阈值确定边缘。
本文设置梯度值的高阈值为Th=22,低阈值为Tl=10,图3为Canny算子边缘提取结果。

图3 Canny算子边缘提取结果
从图3可知,通过Canny算子获得了较完整的零件外圆边缘,但通过放大的小窗口可知,提取的边缘是像素级的,放大后呈锯齿状。此时测得的外圆圆心像素坐标为(583,792),直径大小为D=1 032 pix。
2.2.2 椭圆曲线拟合法
由于本文要检测的亚像素边缘是圆形,故采用椭圆最小二乘拟合法[6]进行边缘提取可以达到较好的精度和速度。
设一个二次曲线方程为:
x2+2Bxy+Cy2+2Dx+2Ey+F=0
(2)
(3)
(1+C)(CF+2BDE-D2C-B2F-E2)<0
(4)
如果式(3)和式(4)同时满足,式(2)就代表一个椭圆,其均方差为:
(5)
分别对式(5)中的B、C、D、E、F求偏导数,并令每个导数式都为零,这样,我们就得到了5个方程组,用矩阵求逆法求出椭圆的参数。
椭圆的中心坐标计算公式为:
(6)
(7)
图4为通过椭圆拟合法求取零件的亚像素精度边缘结果。
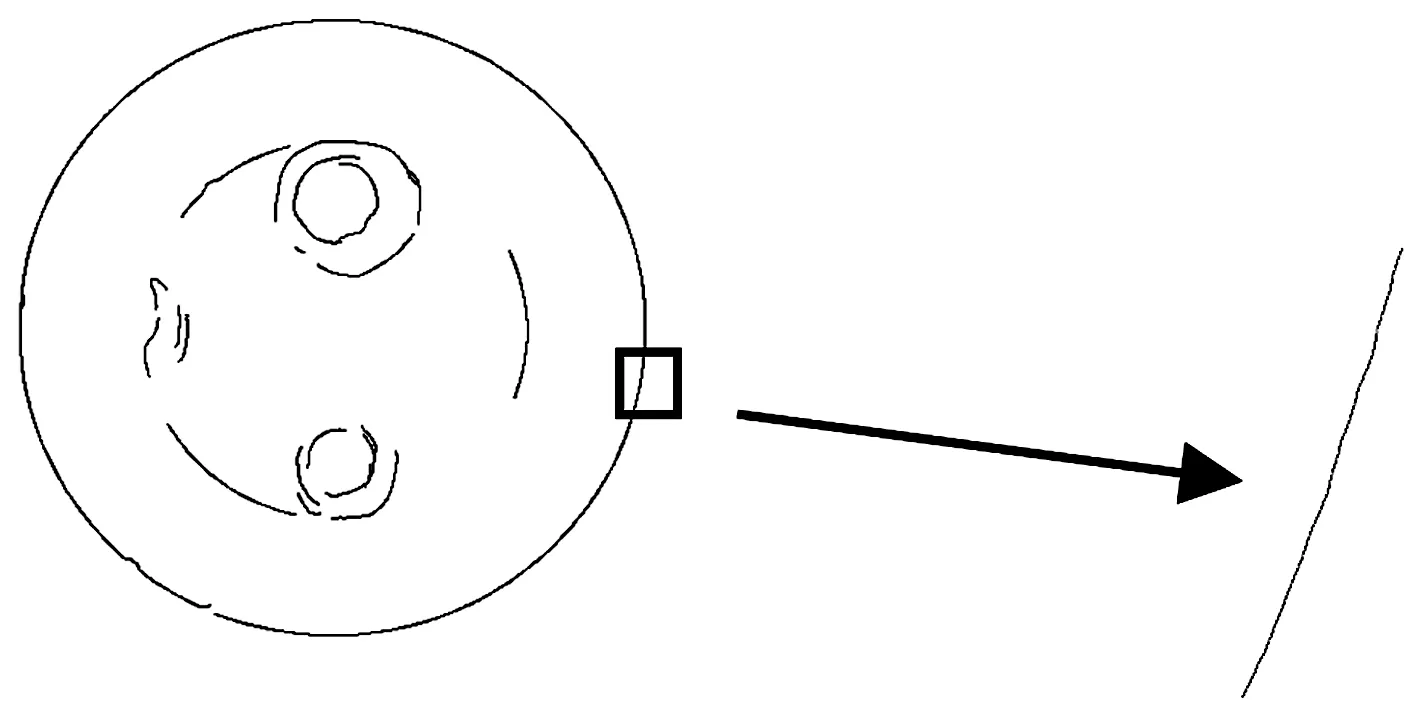
图4 亚像素边缘提取结果
由图5可知,亚像素精度边缘不受像素大小限制,边缘提取精度更高。由此测得的外圆圆心像素坐标为(582.056,791.754),直径为D=1 033.848 pix。
2.3 相机标定
机器视觉系统识别物体的位置和形状等信息,需要确定空间位置与图像上像素的映射关系,以及相机的内部参数和位置参数,即相机标定。相机标定有很多方法,例如:直接线性法(DLT)、基于径向排列约束的标定法(RAC)和张正友标定法等[7-9]。
2.3.1 成像几何模型及坐标变换
由于本系统零件装配的精度要求较高,需要考虑镜头的加工与装配误差导致的非线性畸变,考虑非线性畸变的成像几何模型如图5所示。
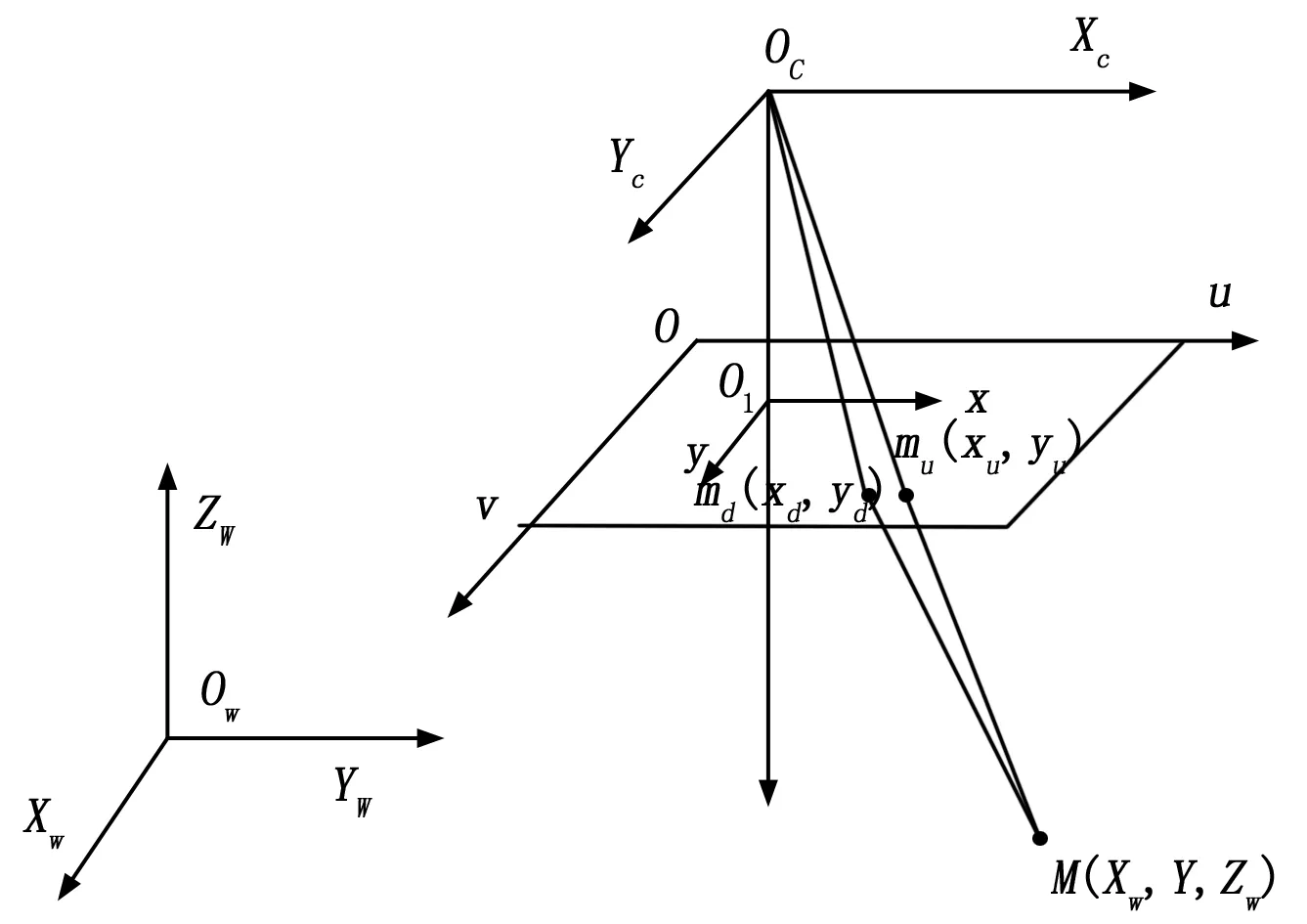
图5 非线性几何模型
空间中点M在世界坐标系(WCS)即owXwYwZw下表达为M(Xw,Yw,Zw),相机坐标系(CCS)为OcXcYcZc,像素坐标系(IPCS)为Ouv,理想情况下点M在图像坐标系(ICS)即O1xy下表示为mu(xu,yu),在实际情况下,相机成像几何模型存在畸变,导致点M成像在Md(xd,yd)。
按照理想的针孔透视模型,图像坐标系(ICS)与像素坐标系(IPCS)的转换关系为:
(8)
其中:(u0,v0)表示在像素坐标系下图像坐标原点的坐标,dx和dy分别为每个像素在图像平面x轴和y轴方向上的物理尺寸大小。
图像坐标系与相机坐标系的转换关系为:
(9)
式中,f为相机的焦距。
相机坐标系与世界坐标系的转换关系为:
(10)
式中,R是3*3的正交旋转矩阵,t表示三维平移向量,R和t的形式如下:
其中:R是α,β,γ的函数,表示如下:


将式(8)、式(9)和式(10)综合起来有:
(11)
式中,cx和cy分别表示图像水平和垂直的尺寸因子,ρ表示比例因子,H1矩阵中包含焦距、主点的坐标等相机的内部结构决定的参数,因而称其为内部参数矩阵,cx、cy、u0、v0叫做相机内部参数。H2成为相机的外部参数矩阵,因为其中包含的旋转矩阵R和平移向量t是由相机的坐标系相对于世界坐标系的位置决定的,相机标定的目的就是确定相机的内部参数与外部参数。
2.3.2 畸变模型
普通工业镜头存在径向畸变、离心畸变和薄透镜畸变,其中径向畸变是影响视觉精度的主要因素,薄透镜畸变可充分地近似为径向畸变。本文首先针对相机镜头存在的径向畸变建立畸变模型,并采用RAC标定法进行标定。为了进一步提高并保证装配精度,针对相机镜头可能存在的径向畸变以及离心畸变,建立存在两种畸变的畸变模型,再采用张正友标定法进行相机标定,并且对比两种方法的标定结果。
(1)径向畸变模型:
将径向畸变量考虑进成像几何关系中,并采用LENZ畸变模型[10],该畸变模型通用性强、精度高,用式12来描述相机的该畸变模型,当k为负值时表示桶形畸变,k为正值时为枕形畸变:
(12)
其中:(x,y)为相机理想的线性模型下的图像点的图像坐标值,(xd,yd)为发生畸变后得到的图像坐标值。
(2)混合畸变模型:
通过张正友相机标定法来解决相机镜头带来的径向畸变以及离心畸变,式(13)用来描述两种畸变的模型,式中包含k1,k2,k3的项表示径向畸变,包含p1,p2的项表示离心畸变。
(13)

2.3.3 相机标定实验
本文基于Halcon图像处理平台进行相机标定实验,标定所用的标定板一般有棋盘方格和圆形靶标[11]等,本文选用圆形靶标的标定板,相对于棋盘方格的角点提取,圆心提取算法抗噪声能力强,算法简单快速。标定板由7*7的圆点及左上角确定坐标系方向的黑色三角形块构成,如图6所示。
进行相机标定时,标定精度与图像数量有关,至少需要10幅图像,为了保证节省标定耗费时间,更适应于工业应用,本文只用10幅图像进行标定,所选图像中标定板的位置应该能覆盖视野的4个角,因为角落处的镜头畸变最大,这样能得到较准确地畸变参数。
拍摄的10幅标定图像如图6所示,并通过重投影法分析标定结果的平均误差,如式14,式15所示。
(14)
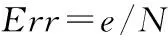
(15)
式中,e表示均方误差;Io(i)表示原始图像上第i点的向量,Ip(i)表示重投影图像上第i点的向量,i∈(0,N);N代表标志点总数,本文N=10*7*7=490;Err表示平均均方误差。

图6 标定图像
RAC标定法与张正友法对内部参数的标定结果如表1所示,外部参数标定结果如表2所示。

表1 相机内部参数标定结果

表2 相机外部参数标定结果
由表1可知,通过张正友相机标定法,将径向畸变与离心畸变加入畸变模型,对相机进行标定,相对于RAC标定法仅考虑径向畸变的畸变模型,减小了相机标定平均误差,平均误差从0.525%减到0.434%。通过测量两种方法的选用相同的10幅标定图像进行标定所用的时间,RAC法需用4 451ms,张正友法则需用5 324ms,虽然采用张正友法需要的时间比RAC法所花的时间多873ms,但张正友法提高了相机标定精度,故本系统采用张正友法对相机进行标定。
3 实验与结果分析
本文所研究的视觉定位装配系统需要测量各个零件的直径以及测得零件中心的坐标值用于零件装配。为了验证本系统对零件直径测量的精度,现对1套装配体中的零件进行测量,每套装配体除底座外包括7中不同的零件需要测量,并且对每个零件测量5次,求取平均值测量结果如表3所示。
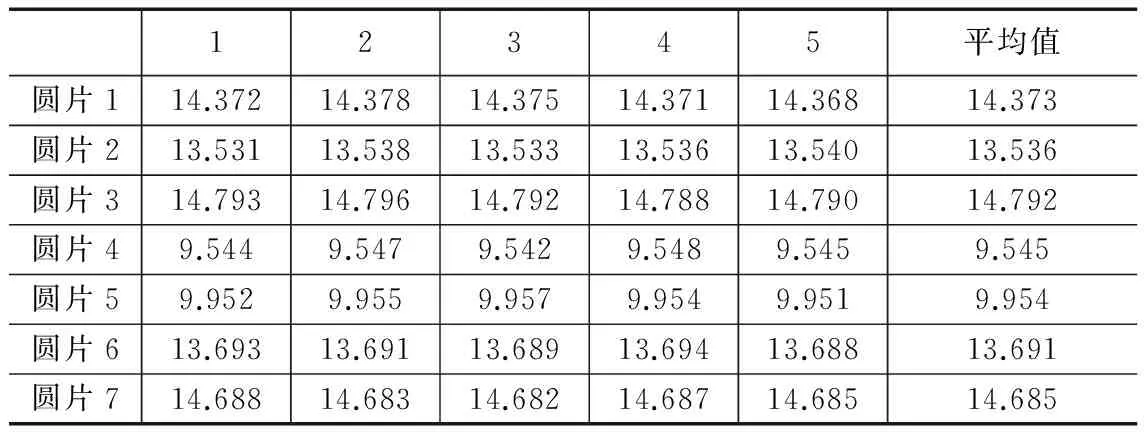
表3 零件直径测量结果 mm
根据公式16,求取测量7种零件直径的标准差σ,计算结果如表4所示。
(16)

表4 零件直径标准差 mm
从表4中可以得出,7种零件直径测量尺寸中,最大标准差σmax=0.003 8mm,满足工业要求。
为了对零件中心的视觉定位精度进行验证,随机选取一个底座,针对该底座反复装配3次,通过测量各零件中心定位坐标来得到同轴度精度,并且与未加入视觉定位系统的装配精度进行对比,首先测得底座的中心像素坐标为(793.672,607.154),装配结果分别如表5,表6所示。
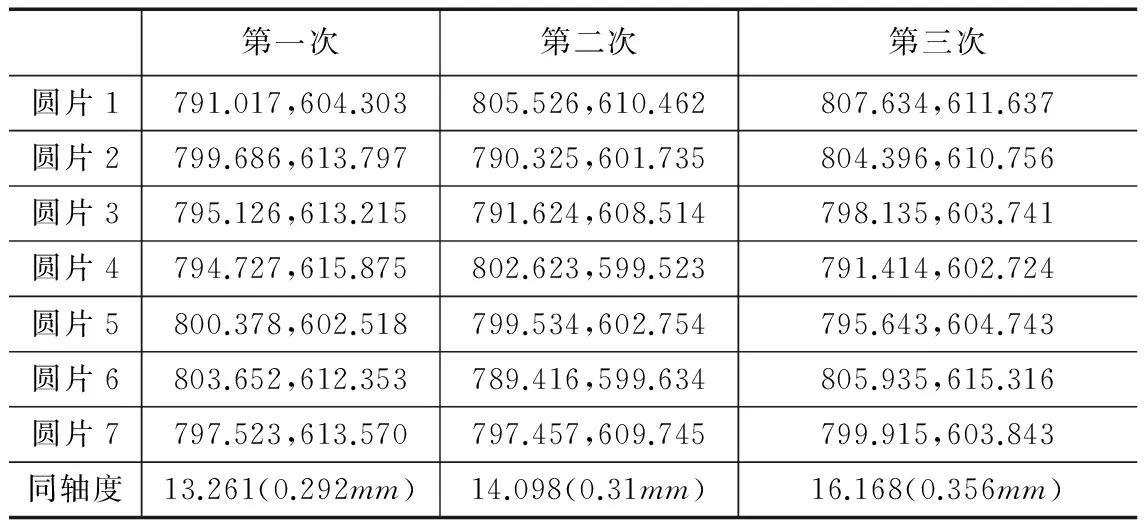
表5 未引入视觉定位的装配结果 pixel

表6 引入视觉定位的装配结果 pixel
由表5、表6中的同轴度数据可知,未引入视觉定位系统时,装配同轴度误差最大达到0.356 mm,而引入视觉定位系统时,装配同轴度误差最大只有0.011 mm,小于0.05 mm,满足装配同轴度精度的要求。
4 结论
本文基于机器视觉搭建的高精度测量与装配系统,通过结合Canny算法以及椭圆曲线拟合法,提取了零件亚像素精度边缘,为零件尺寸的高精度测量以及零件的高精度装配奠定了基础,通过分析对比张正友相机标定法与RAC标定法的标定结果,得出采用RAC法标定花费的时间比张正友法少,但前者的精度没有后者高。最终本系统获得的零件尺寸测量精度以及装配同轴度精度均满足工业要求,可以解决实际问题。
[1] 王冠英, 胡心平, 刁维龙. 基于机器视觉的复杂形状模具尺寸测量[J]. 计算机测量与控制, 2015,23(3):706-708.
[2] 查 英, 刘铁根, 杜 东, 等. 基于机器视觉的零件自动装配系统[J]. 天津大学学报, 2006,39(6):722-726.
[3] 李钊宝, 汪新新, 贾茜媛. 基于机器视觉的工件尺寸高精度测量方法[J]. 计算机测量与控制, 2015,23(6):1866-1870.
[4] 郭 瑞, 刘振国, 曹云翔, 等. 基于视觉的装配机器人精确定位研究[J]. 制造业自动化, 2014,36(5):154-156.
[5] Casten Steger, Markus Ulrich, Christian Wiedemann. Machine Vision Algorithms and Applications[M].1sted., Yang Shaorong, Wu Dijing, Duan Deshan, translated. Beijing: Tsinghua University Press,2008:97-125.
[6] 张丽群. 基于相关法的多重成像亚像素定位算法的研究与实现[D]. 哈尔滨:哈尔滨工程大学, 2005.
[7] 解则晓, 辛少辉, 李绪勇, 等. 基于单目视觉的机器人标定方法[J].机械工程学报, 2011, 47(5):35-39.
[8] 赵高长, 武风波, 周 彬, 等.基于DLT模型的摄像机标定简化方法[J].应用光学, 2009, 30(4):585-589.
[9] 张 娜. 摄像机标定方法的研究[D]. 南京:南京理工大学, 2014.
[10] Lanser S.Model-based localization based on monocular video images[D]. Technical University of Munich, 1997.
[11] Zhang Z Y. A flexible new technique for camera calibration[J].IEEE Transactions on Patten Analysis and Machine Intelligence, 2000, 22(11):1330-1334.
Design of High-precision Measurement and Assembly System Based on Machine Vision
Jiao Liang,Hu Guoqing,Lü Chengzhi,Zhao Pengfei
(College of Mechanical and Automotive Engineering, South China University of Technology,Guangzhou 510640, China)
In realizing automation production process of certain precision products, there exist the problem of being hard to measure and assemble many kinds of small parts which are necessary for the product high-precision and autamatically. Aiming at the problem, the automatic measurement and assembly system is built based on machine vision technology. Based on Halcon, the image processing software platform, the system pretreats the parts image with median filtering, image enhancement and so on, and uses the Canny algorithm to calculate the pixel-precision edge, then uses elliptic curve fitting method to obtain the subpixel-precision edge. Two kinds of camera lens distortion model are established, using the method of the radial alignment constraint (RAC) and the method of Zhang Zhengyou to calibrate cameras and compared the calibration accuracy. The experimental results show that the assembly alignment accuracy of system can reach 0.05 mm, and the standard deviation of measurement is less than 3.8 μm. It can meet the requirement of industry and solve practical problems.
machine vision; automatic assembly; sub-pixel accuracy; distortion model; camera calibration
2016-01-16;
2016-02-15。
广东省教育部产学研结合项目(2012B091100109)。
焦 亮(1990-),男,江西吉安人,硕士研究生,主要从事智能机器人与图像处理技术方向的研究。
胡国清(1964-),男,四川崇庆人,教授,博士导师,主要从事智能机器人与图像处理技术方向的研究。
1671-4598(2016)07-0072-04
:10.16526/j.cnki.11-4762/tp
TP391.41 文献标识码:A
