沥青路面结构足尺力学响应实测与仿真
2016-10-28张怀志任俊达
张怀志, 任俊达, 纪 伦, 王 磊
(1. 高速公路养护技术交通行业重点实验室(辽宁省交通科学研究院), 沈阳 110015; 2.哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090; 3.辽宁省交通厅公路管理局, 沈阳 110005)
沥青路面结构足尺力学响应实测与仿真
张怀志1, 任俊达1, 纪伦2, 王磊3
(1. 高速公路养护技术交通行业重点实验室(辽宁省交通科学研究院), 沈阳 110015; 2.哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090; 3.辽宁省交通厅公路管理局, 沈阳 110005)
为探究沥青路面在荷载作用下力学响应,通过基于辽宁省沥青路面足尺加速加载试验,开展路面结构力学仿真方法及力学响应特征研究. 采用光纤光栅传感器实测足尺加速加载路面的面层底部、基层底部和路基顶面的力学响应,利用单轴压缩动态模量试验获取沥青混合料的粘弹性参数,通过FWD弯沉盆反算得到基层及土基的弹性模量,利用接触痕迹得到轮胎的接触面分布;通过单轴压缩动态模量试验及四点弯曲动态模量试验对传感器进行了标定. 在此基础上,采用有限元软件ABAQUS建立基于实测参数的路面结构力学仿真模型,分析路面结构在不同加载位置和速度下的力学响应,并与实测结果进行对比. 结果表明:所建立的路面力学仿真模型能较合理地模拟沥青层底三向应变、半刚性材料层底纵向、横向应变以及土基顶面的压应力. 沥青混合料粘弹特性导致弹性后效,使力学响应曲线表现出非对称特点. 随着温度的增加和加载速度的减小,沥青层底三向应变、半刚性基层底的水平应变以及土基顶面压应力的响应幅值增加.
铺面工程; 加速加载试验; 三维粘弹有限元; 路面力学响应; 仿真模型
路面结构力学响应分析是沥青路面力学-经验设计方法的核心. 当前我国沥青路面结构设计力学分析的理论基础是静态层状弹性体系,通过限制路表弯沉、沥青层底和基层底的弯拉应力来保证路面结构的疲劳寿命[1]. 然而,随着交通轴载和车辆速度的增加,路面结构的动态特征显著,导致静态层状弹性力学分析方法难以解释新条件下沥青路面的破坏现象[2-3]. 考虑车辆荷载的动态效应进行路面结构力学响应分析方法分为两大类:瞬态分析和粘弹性分析. 瞬态分析方法基于沥青路面层状弹性体系结构的基本假定以及Hamiton原理,考虑路面结构阻尼的影响. 对于路面结构中的阻尼,由于其机理复杂,通常采用瑞利阻尼假设,基于经验公式计算阻尼系数[4-7]. 限于对阻尼研究的不足,该方法的应用仍需进一步探讨. 对于粘弹性分析方法,重点考虑沥青混合料的粘弹特性,忽略结构阻尼和惯性的影响,采用粘弹本构关系,将沥青混合料的粘弹参数引入结构分析模型,排除了假定阻尼参数的影响,更好地反映沥青混合料的实际工作状态,分析结果具有较好的合理性[8-11]. 然而,大部分粘弹性分析研究仍停留在定性分析阶段,缺乏计算值与实测值的对比和验证,其结论具有局限性,难以保证路面力学响应分析的准确性和可靠性.
为消除分析模型中假定参数的影响,以辽宁省高速公路典型沥青路面足尺加速加载试验结构为研究对象,建立了基于实测参数的三维有限元仿真模型. 采用室内试验方法,得到沥青混合料的粘弹参数;利用FWD弯沉盆反算得到基层和土基的弹性模量;实测了加速加载试验设备MLS 66加载轮胎接触面积分布. 采用光纤光栅传感器,对结构内部力学响应进行实时监测. 通过计算值与实测值对比,对所建立的路面力学仿真模型进行验证;并进一步分析了路面结构内部力学响应特点及其受温度和加载速度的影响.
1 路面结构参数及力学响应测量
按照辽宁省典型的高速公路沥青路面结构形式铺筑了5 m×40 m加速加载试验段,试验段路面结构为3.5 cm SMA13+6 cm AC20+8 cm AC25+20 cm水泥稳定碎石+20 cm水泥稳定碎石+15 cm级配砂砾+土基. 采用MLS 66加速加载试验系统,对路面进行加速加载试验. MLS 66具有自行移动功能,依靠直线感应电机可实现较高的加载频率,最大加载速度为6 000次/h,相当于22 km/h的行车速度.
为能获取路面结构内部的力学响应,在加速加载试验路进行了光纤光栅应力应变传感器及环境参数传感器的现场埋设,对面层和基层底部的三向应变及土基顶面压应力进行采集,同时实时采集路面结构内部温湿度状况. 传感器沿加载段中心线布设,采用双轮荷载进行加载,轴载150 kN. 加载位置包括正载和偏载两种方案,正载是指荷载单元双轮中心位置位于传感器纵断面正上方;偏载是指荷载单元单轮中心位置位于传感器纵断面正上方.
所采用的光纤光栅传感器模量(一般为50~70 GPa)与沥青混合料模量(一般为1.0~1.2 GPa)相差较大,高模量传感器的存在使其附近区域的应力场和应变场重新分布,导致其测定的结果与真实值存在差异,而评价光纤光栅传感器与沥青混合料间协调变形性能是解决其在路面中应用的前提和基础. 为此专门设计了室内试验对传感器的协调变形能力进行评估,如图1、2所示.
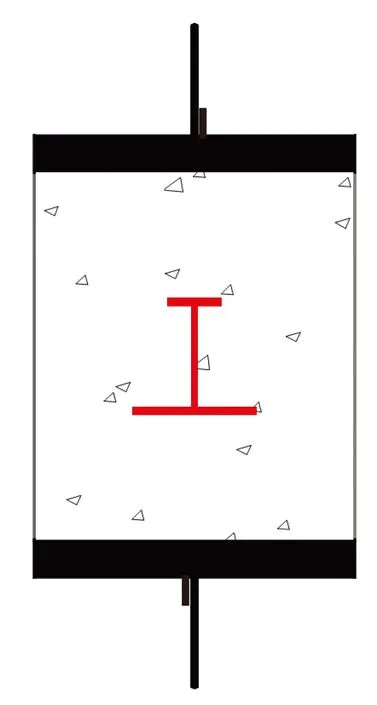
图1 单轴压缩动态模量试验
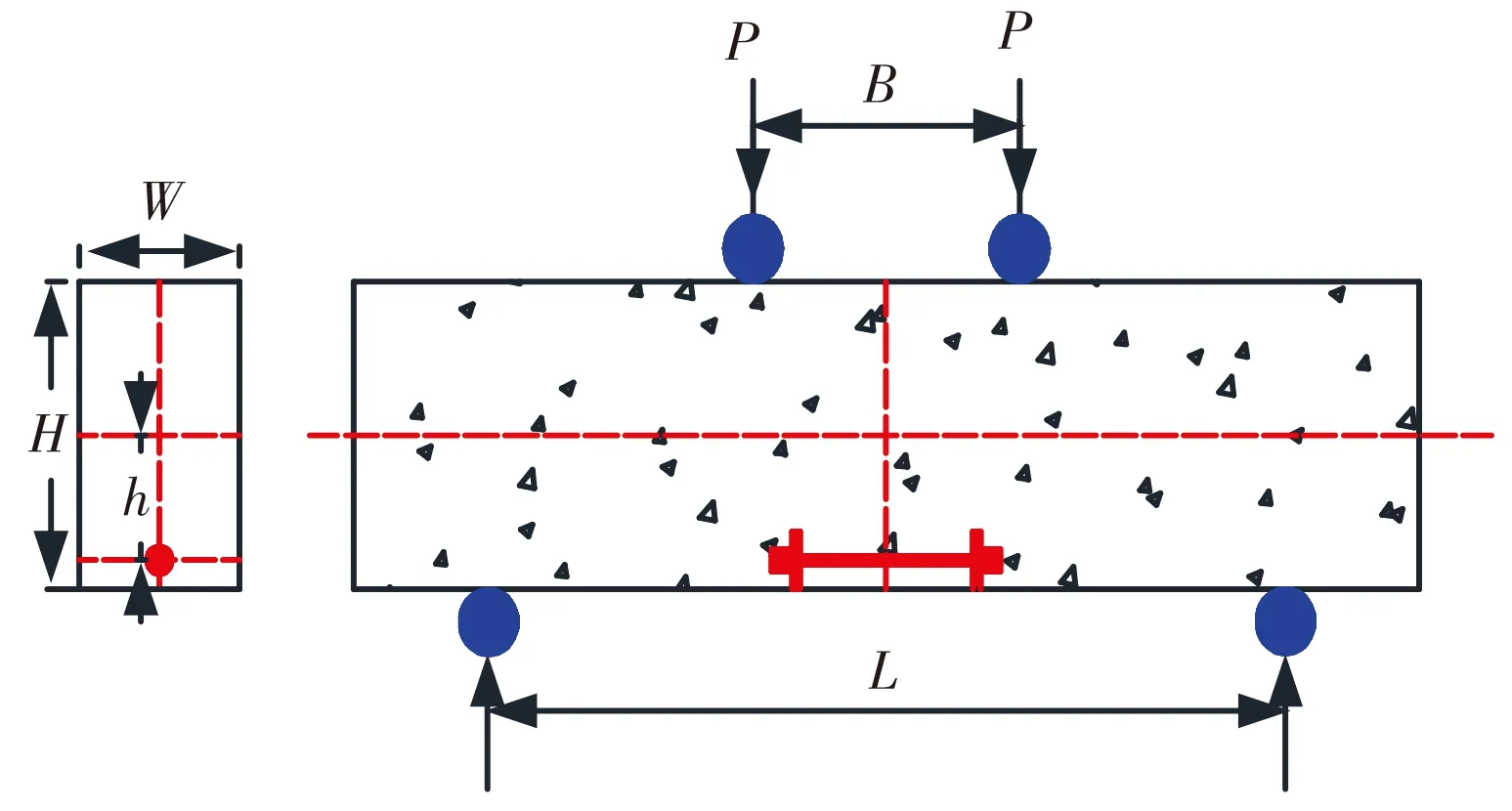
图2 四点弯曲动态模量试验
在单轴压缩动态模量试验与四点弯曲动态模量试验的试件中分别埋入光纤光栅传感器,传感器布置见图1、2. 同时在试验过程中,利用固定在试件表面的LVDT传感器,同步记录试验过程中试件的变形量,进而对两种测试结果进行对比分析. 两种测试方法下的部分试验数据对比结果如图3、4所示.

图3 FBG传感器与LVDT测试结果对比
对于测试结果,采用一个三角函数与线性函数的组合对变形量与时间进行拟合,得

(1)
式中: y为拟合值;a、ω、φ分别为正弦函数峰值、角频率及相位角;b、c分别线性函数的为斜率、截距.
对图3中数据,拟合结果如下:ωFBG=125.4(R2=0.88), ωLVDT=125.5(R2=0.98). 角频率的变化表征FBG传感器同步变形的能力,由数据可知,FBG传感器的变形响应基本与LVDT一致,没有滞后性.
由图4分析FBG传感器变形的线性特征. 良好的线性特性意味着传感器的协同变形能力的稳定性. 可以看出,在不同的应变水平下,FBG传感器的波长变化与实际应变保持良好的线性相关性,相关系数R2=0.99.

图4 不同应变水平下FBG传感器波长变化与实际应变对比Fig.4 Wave length contrast between FBG and real strain of varying strain
由上述分析可以看出,所采用的FBG传感器可以与沥青混合料产生良好的协调变形,经标定后,满足现场测试的需要. 沥青混合料是一种具有复杂粘弹特性的复合材料,对沥青混合料和沥青路面结构进行粘弹性分析可以更客观地反映其行为特性. 为准确获取沥青混合料粘弹参数,利用UTM-100材料试验系统,采用应力控制方式,分别对SMA13、AC20、AC25混合料试件施加正弦荷载,测定其复数模量. 根据时间-温度等效原理[12],确定了3种沥青混合料的动态模量主曲线(如图5~7所示),同时得到各个温度下的时间-温度位移因子αT,如图8所示.
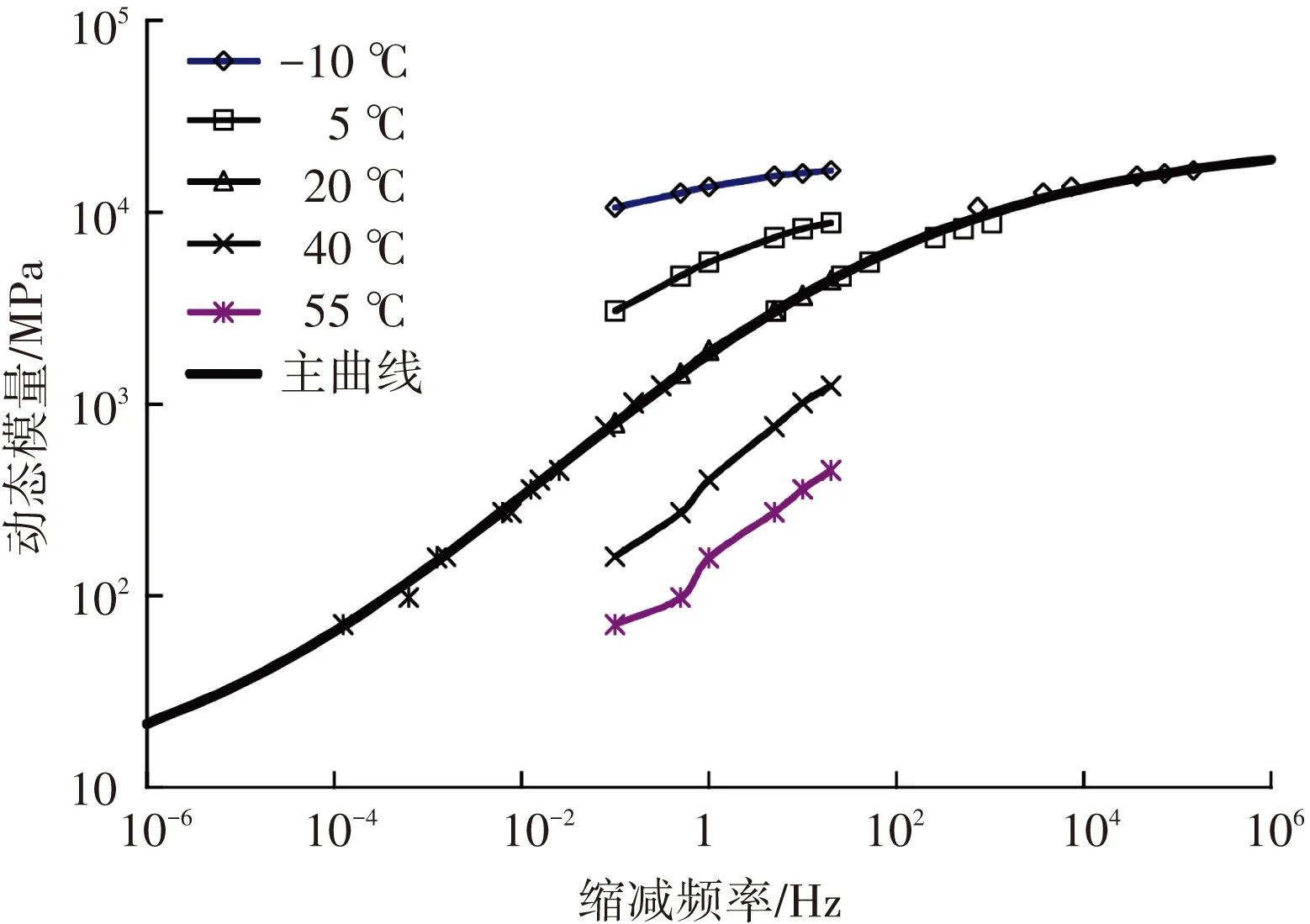
图5 SMA13动态模量主曲线
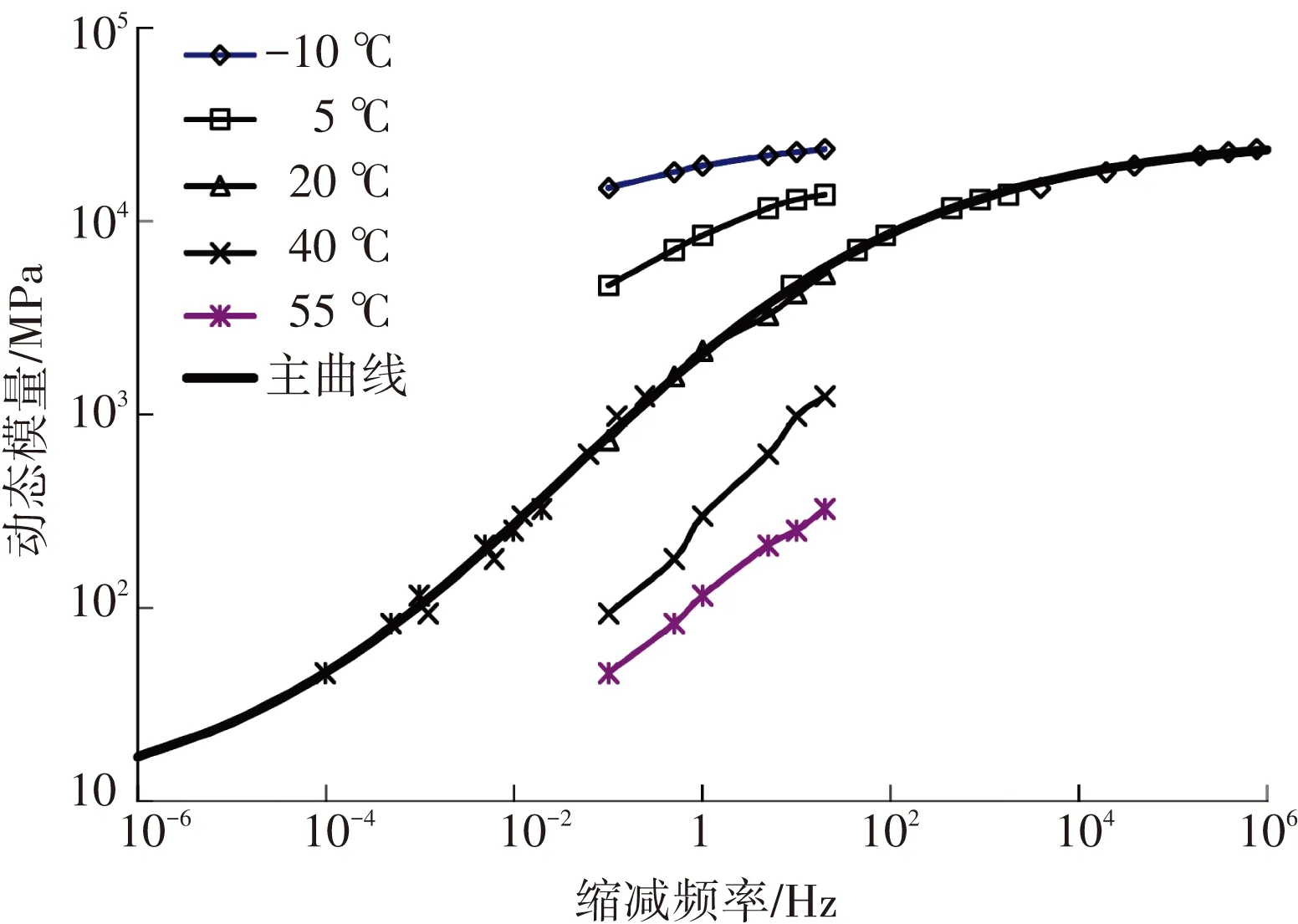
图6 AC20动态模量主曲线

图7 AC25 动态模量主曲线
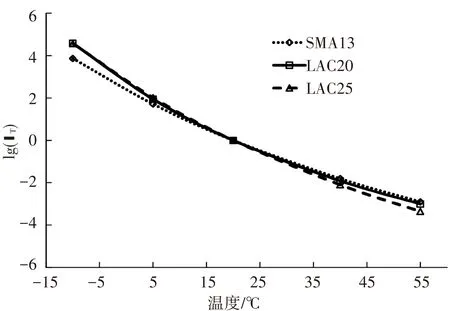
图8 时间-温度位移因子与温度的关系
根据Boltzmann叠加原理,粘弹性材料有如下的本构关系为
(2)
式中:E(t)为松弛模量;σ为应力;ε为应变;t为缩减时间;τ为积分变量.
利用沥青混合料不同温度和荷载频率下复数模量试验结果,通过Wiechert模型确定松弛模量[13]. 转换后,可将松弛模量表示为Prony系列,即
(3)
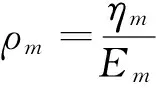
基层及土基弹性模量通过FWD弯沉盆反算得到. 在加速加载试验段的11个测点进行了FWD试验. 模量反算采用EVERCAL软件. 在FWD模量反算中,将水稳碎石和水稳砂砾作为一层(半刚性材料层),将垫层和土基作为一层. 实验中得到半刚性材料模量的平均值为1 635.3 MPa,变异系数为11.2%;土基模量平均值为124.7 MPa,变异系数为12.7%.
2 有限元仿真模型的建立
基于大型有限元软件ABAQUS建立仿真模型. 假设各沥青混合料层为均质、各向同性的粘弹性材料;水稳基层及土基为均质、各向同性的线弹性材料. 对于沥青混合料,利用前面试验得到粘弹力学参数;而对于半刚性材料和土基的模量直接采用FWD模量反演结果.
轮胎接触压强的分布对路面结构内部力学响应存在显著影响[14]. 加载轮胎接地面积采用实际测定,接地压力分别为0.69、0.86、0.9、0.86、0.69 MPa. 由于结构和荷载的对称性,取1/2结构建立模型. 对于本研究的问题,有限元模型必需足够大,才能保证得到路面结构内不同深度处完整的应力波形,并且当轮载在路面上移动时,可以消除边界条件的影响. 通过试验分析,确定有限元模型在长度、宽度和深度方向的尺寸分别为8.0、4.0、5.0 m. 采用三维六面体八节点等参元,将路面结构划分为47 040个单元,共51 540个节点. 各层层间状态为完全连续. 除了对称边界条件外,底面和侧面均为法向完全约束. 对于行车荷载的模拟详见文献[15].
3 力学响应实测与计算比较分析
3.1沥青层底
图9为不同轮载行驶速度下,正载和偏载作用下沥青层底竖向应变随时间的变化规律. 如图所示,计算值与实测值表现出了类似的变化趋势. 当轮载从远处驶向分析点时,沥青层底承受较小的拉应变,此时计算的拉应变稍大于实测压应变;随着轮载进一步靠近,拉应变转为压应变,并逐渐到达峰值;而后当荷载驶离时,该点从受拉状态快速恢复至初始状态. 从上述过程可以看出,路面在车辆驶过前后,经历了拉-压的交替变化,力学响应曲线呈现出显著的非对称性,且拉应变相对于压应变而言是不可忽略的. 计算的压应变峰值普遍小于或接近实测值,不同行驶速度下表现出相同的趋势.

(a) 正载作用下沥青层底竖向应变

(b) 偏载作用下沥青层底竖向应变
图10、11为不同轮载行驶速度下沥青层底纵向应变和横向应变的实测值和计算值. 由于在正载工况下,通过轮隙中心沿行车方面的平面为对称面,在对称面上横向应变为0,因此,本研究不进行正载下横向应变的分析. 当轮载经过路面结构时,与压应变不同,沥青层底的水平应变会经过受压、受拉、再受压的变化过程. 对于纵向应变,在轮载驶离过程中,计算的压应变大于实测值. 对于横向应变,在轮载趋近过程中,实测压应变大于计算值.
3.2半刚性材料层底
图12为水稳砂砾层底正载和偏载下纵向应变的实测值和计算值,由图可知,在轮载趋近和驶离过程中,计算值和实测值很接近,力学响应曲线基本呈现对称性,响应持续时间较长,计算得到的峰值较实测值稍小. 图13为水稳砂砾层底水平横向应变计算和实测的时程曲线,可以发现,计算值和实测值不论是峰值还是曲线形状符合度均较好.
3.3土基顶面
图14为正载和偏载下土基顶面压应力的实测值和计算值. 由图可知,计算值与实测值在不同荷载位置和加载速度下均非常接近. 随着轮载趋近,路基顶面压应力开始出现并逐渐增大,加载和卸载阶段,其力学响应曲线呈对称状态,基本不受整体结构粘弹性影响.
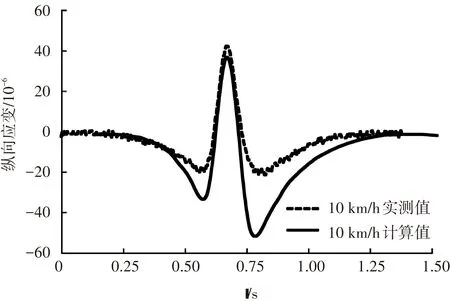
(a) 正载作用下沥青层底纵向应变

(b) 偏载作用下沥青层底纵向应变

(a) 偏载作用下沥青层底横向应变
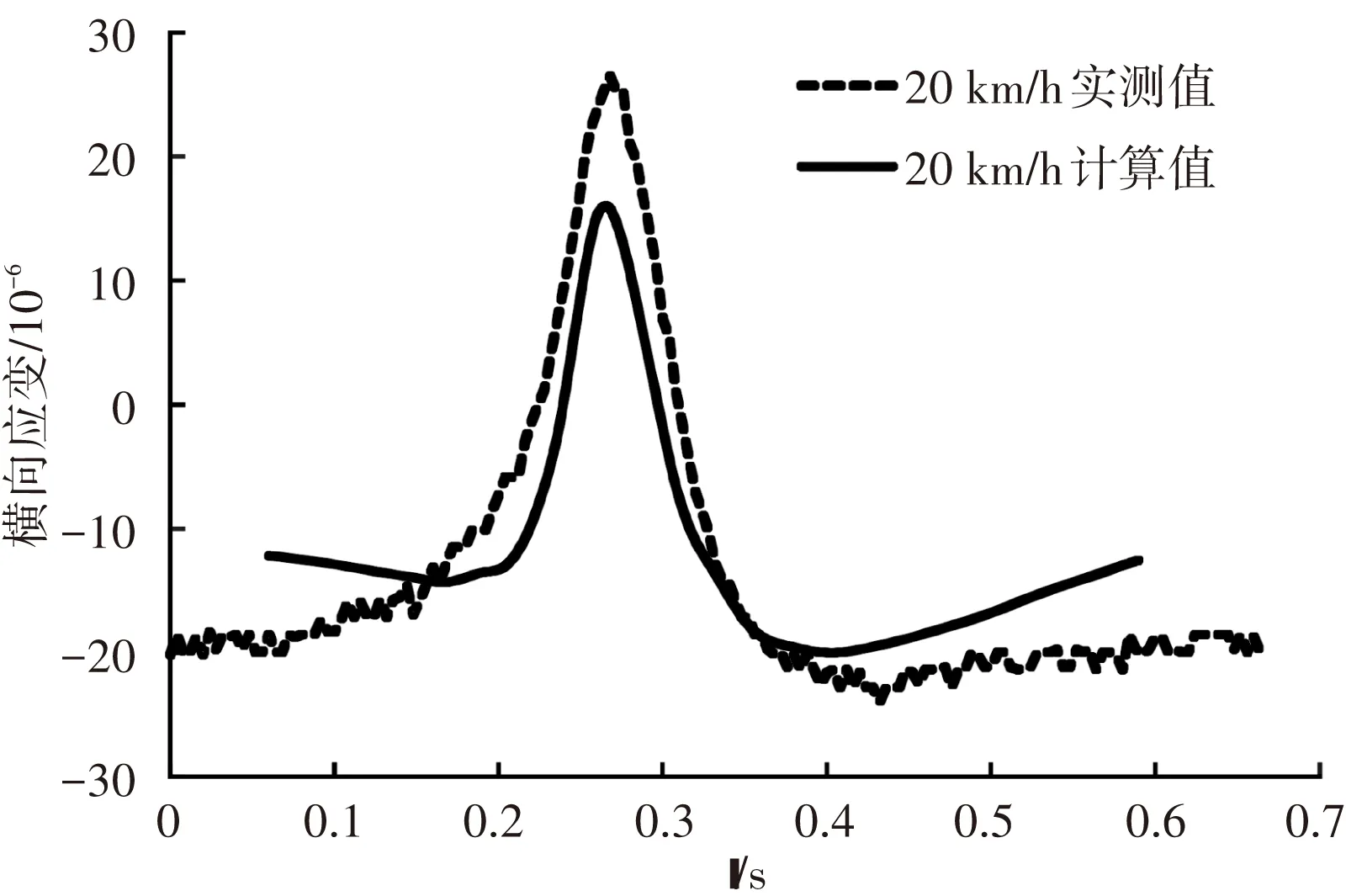
(b) 偏载作用下沥青层底横向应变
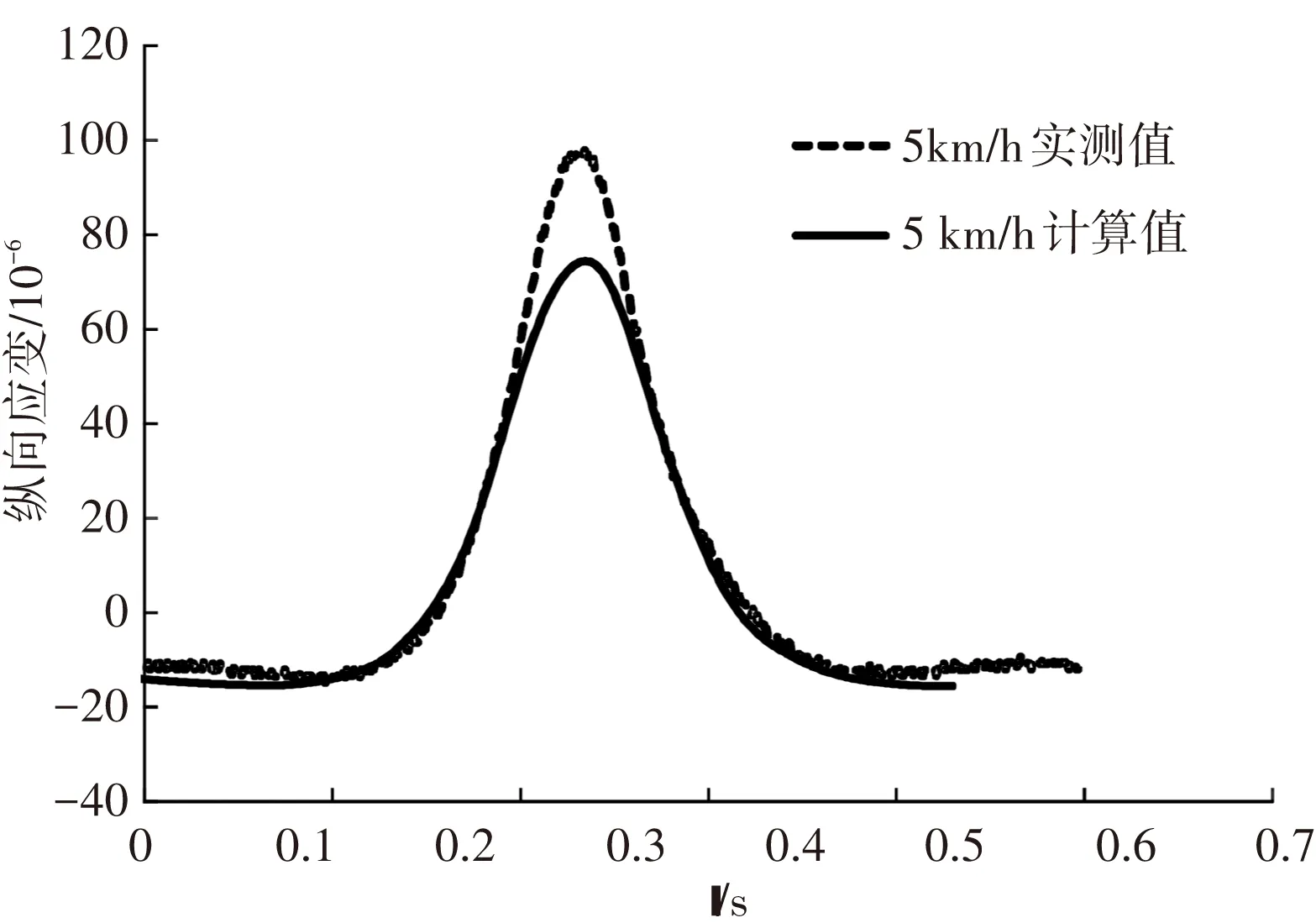
(a) 正载作用下水稳砂砾层底纵向应变
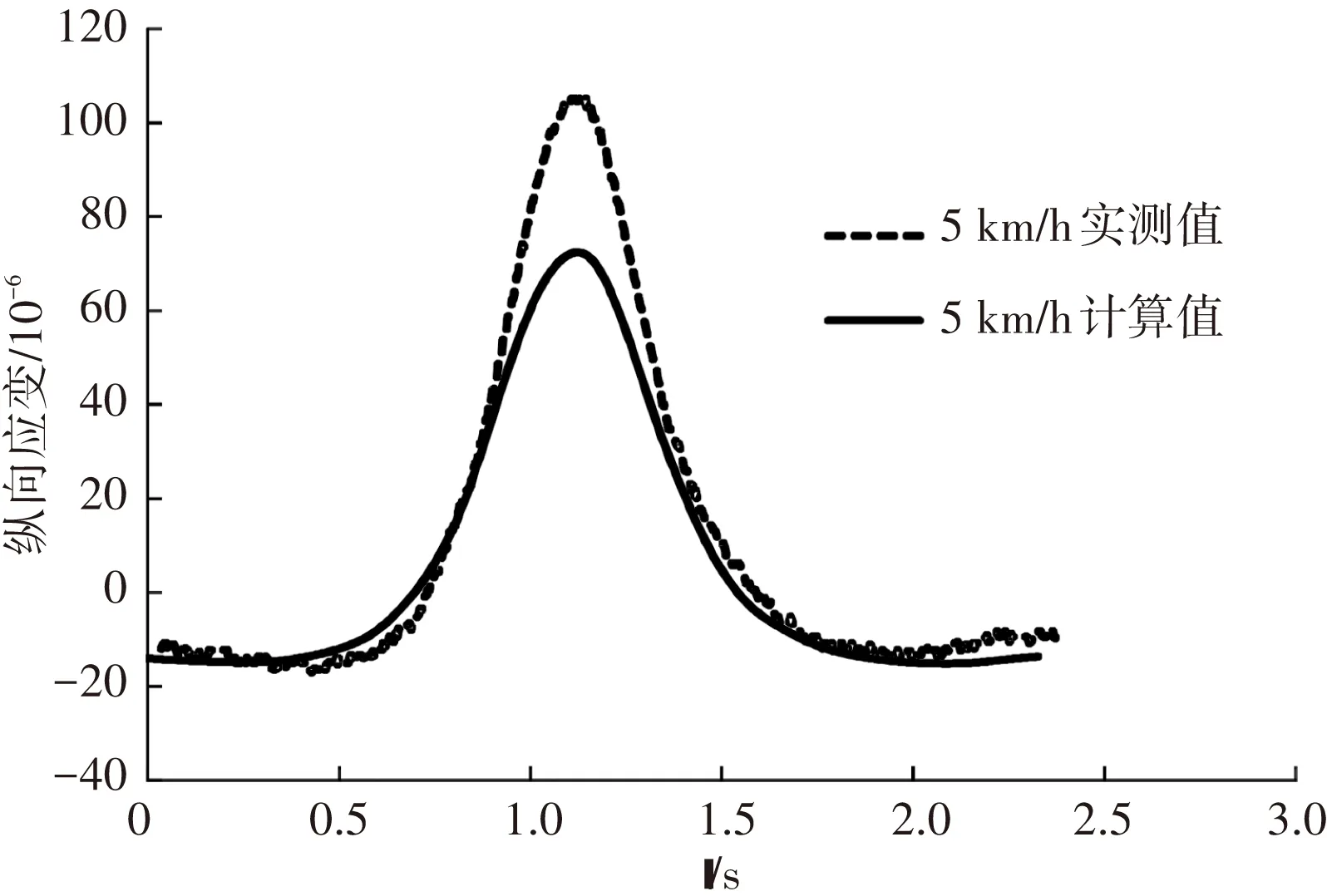
(b) 偏载作用下水稳砂砾层底纵向应变
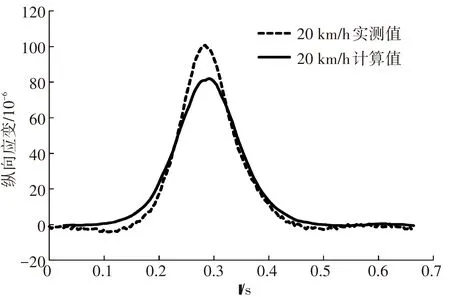
(c) 正载作用下水稳砂砾层底纵向应变

(d) 偏载作用下水稳砂砾层底纵向应变
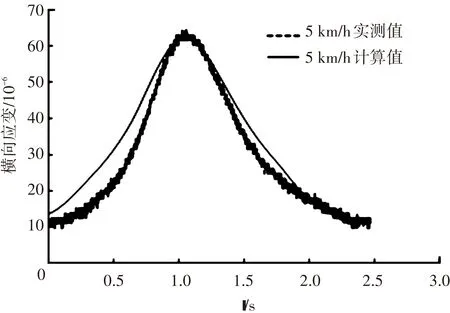
(a) 偏载作用下水稳砂砾层底横向应变
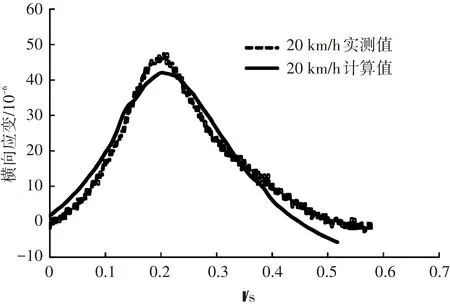
(b)偏载作用下水稳砂砾层底横向应变
由上述分析可以看出,所采用的建模方法和参数可以较好地模拟路面结构在移动轮载作用下不同工况路面结构内部的力学响应变化. 就符合程度而言,路基顶面好于半刚性层底好于沥青层底. 沥青层底部在一些工况下,理论计算值和实测值存在局部的差异,这些误差主要是由传感器的定位精度与埋入材料的协同变形能力等因素所导致. 沥青层底的传感器定位难度较大,与沥青混合料的协同变形能力较为复杂,仍是一个需要深入研究的技术问题[16],而路基中土压力盒的布设则属于较为成熟的方法[17]. 总体而言,整体上所建立的力学仿真模型能够较好符合实测结果,精度满足工程要求,可以较为精确地进行路面结构力学响应分析.
4 温度和行车速度对力学响应的影响
由以上分析可知,利用三维粘弹性有限元可以较好地模拟现场移动轮载作用下路面结构内的力学响应. 本研究中利用该方法分析路面结构内部力学响应随温度和行车速度的变化规律,在分析中采用3个不同温度(10、25、40 ℃)和3个不同行车速度(5、45、90 km/h). 因篇幅限制本文只分析了偏载作用下路面结构层内的力学响应.
图15~17为沥青层底竖向、纵向、横向应变幅值. 可见沥青层内的力学响应受温度和行车速度的影响很大. 随着温度的增加和行车速度的减小,沥青层三向应变幅值增加,并且当温度较高或行车速度较低时,力学响应效果更加明显. 在40 ℃时,当行车速度从45 km/h减小到5 km/h时,竖向应变幅值增加了约250%,剪应变增加了约125%,水平纵向应变增加了约60%,横向应变增加了约195%.
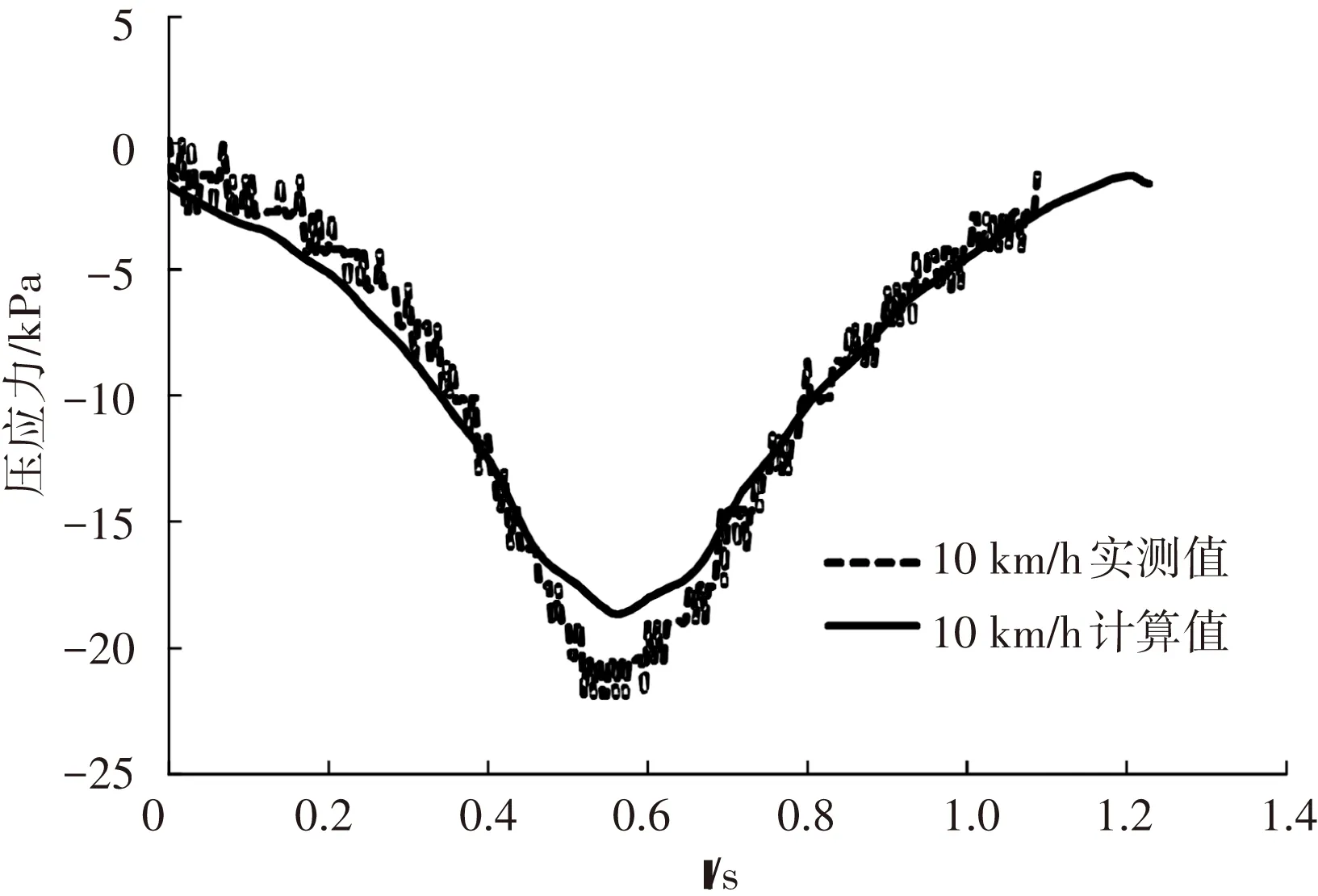
(a) 正载作用下土基顶面压应力
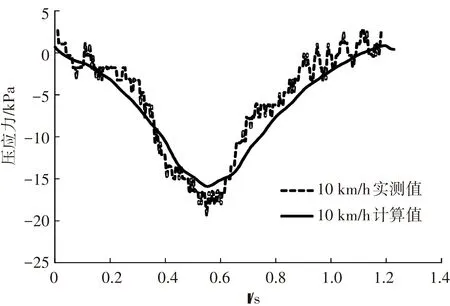
(b) 偏载作用下土基顶面压应力
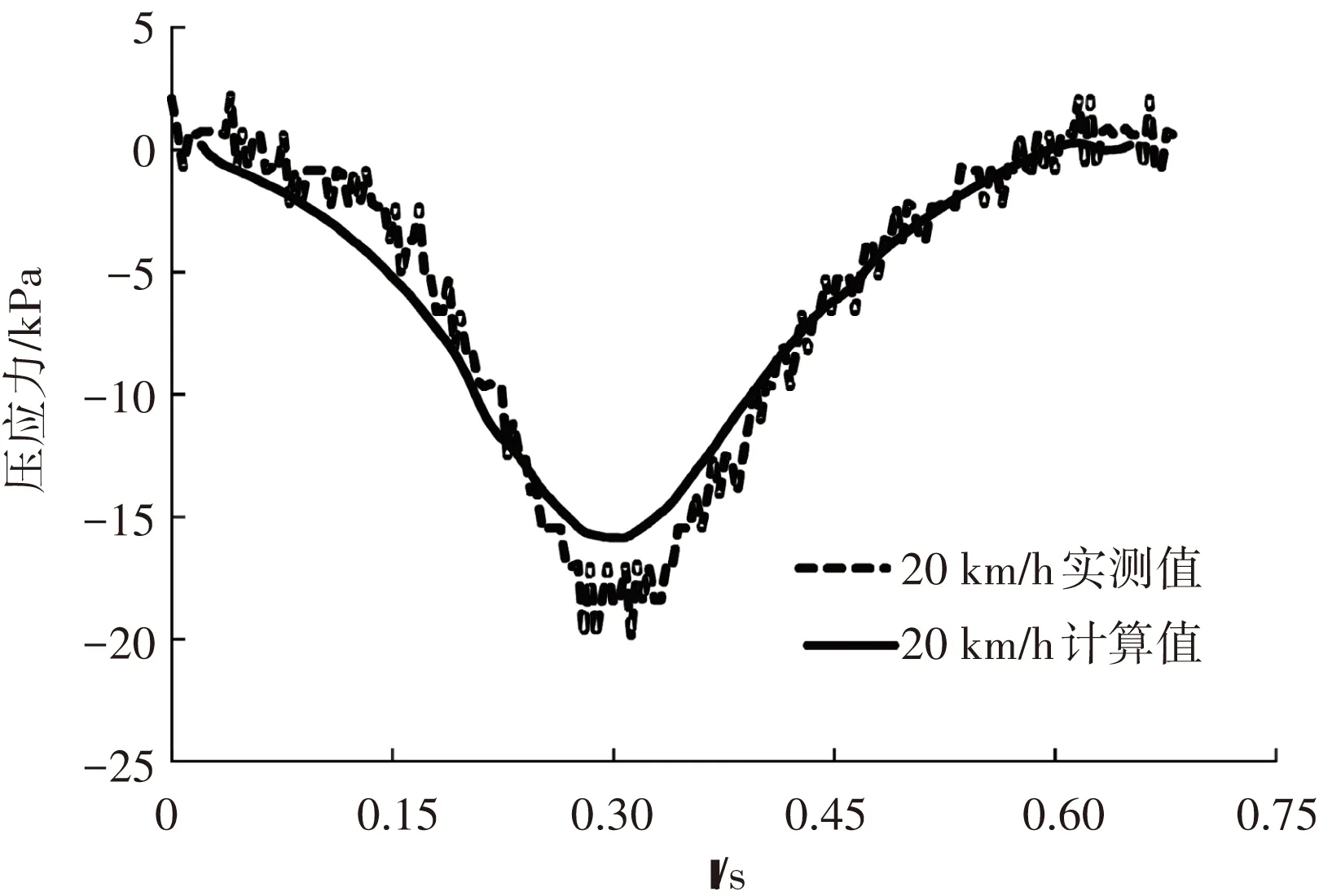
(c) 正载作用下土基顶面压应力
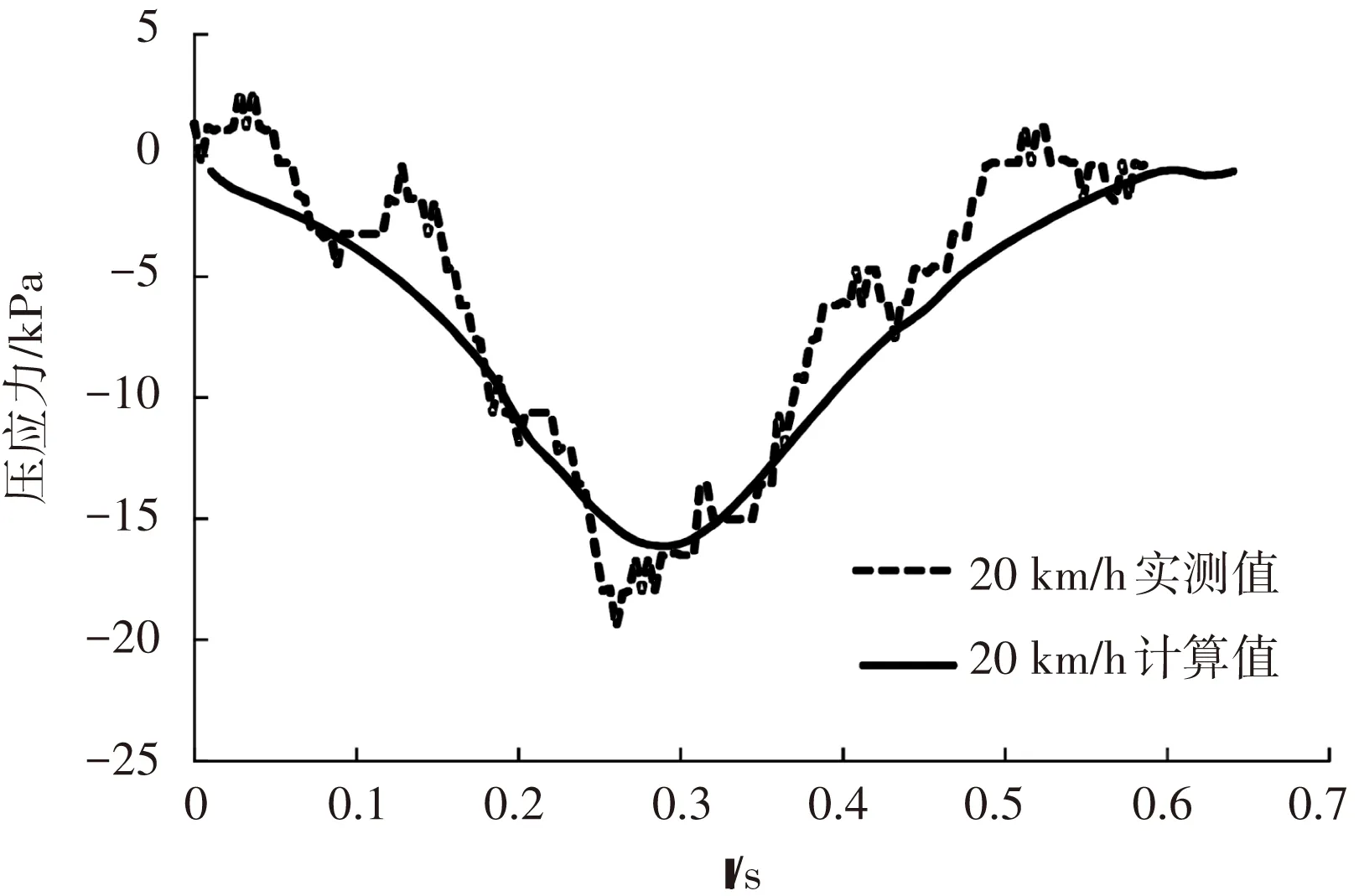
(d) 偏载作用下土基顶面压应力
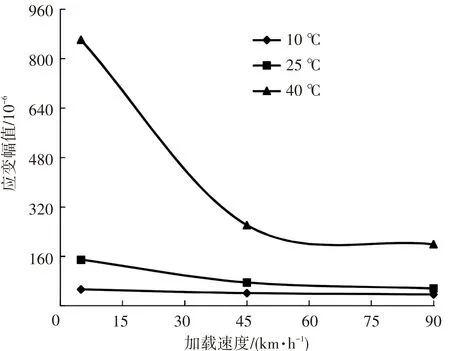
图15 沥青层底竖向应变幅值

图16 沥青层底纵向应变幅值

图17 沥青层底横向应变幅值
图18、19分别为水稳砂砾层底纵向及横向应变幅值随速度和温度的变化曲线. 尽管水稳砂砾材料没有明显的粘弹性质,其力学参数受温度和行车速度的影响很小,但由于温度和行车速度改变了沥青层的力学参数,因此造成了水稳砂砾层底的力学响应的变化. 由图可见,随着温度的增加或行车速度的减小,水稳砂砾层底的水平应变幅值增加,并且当温度较高或行车速度较低时,力学响应增加的效果更加明显. 水稳砂砾层底力学响应增加的幅度没有沥青层底的明显,在40 ℃时,当行车速度从45 km/h减小到5 km/h时,水平纵向应变增加了约20%,横向应变增加了约10%.
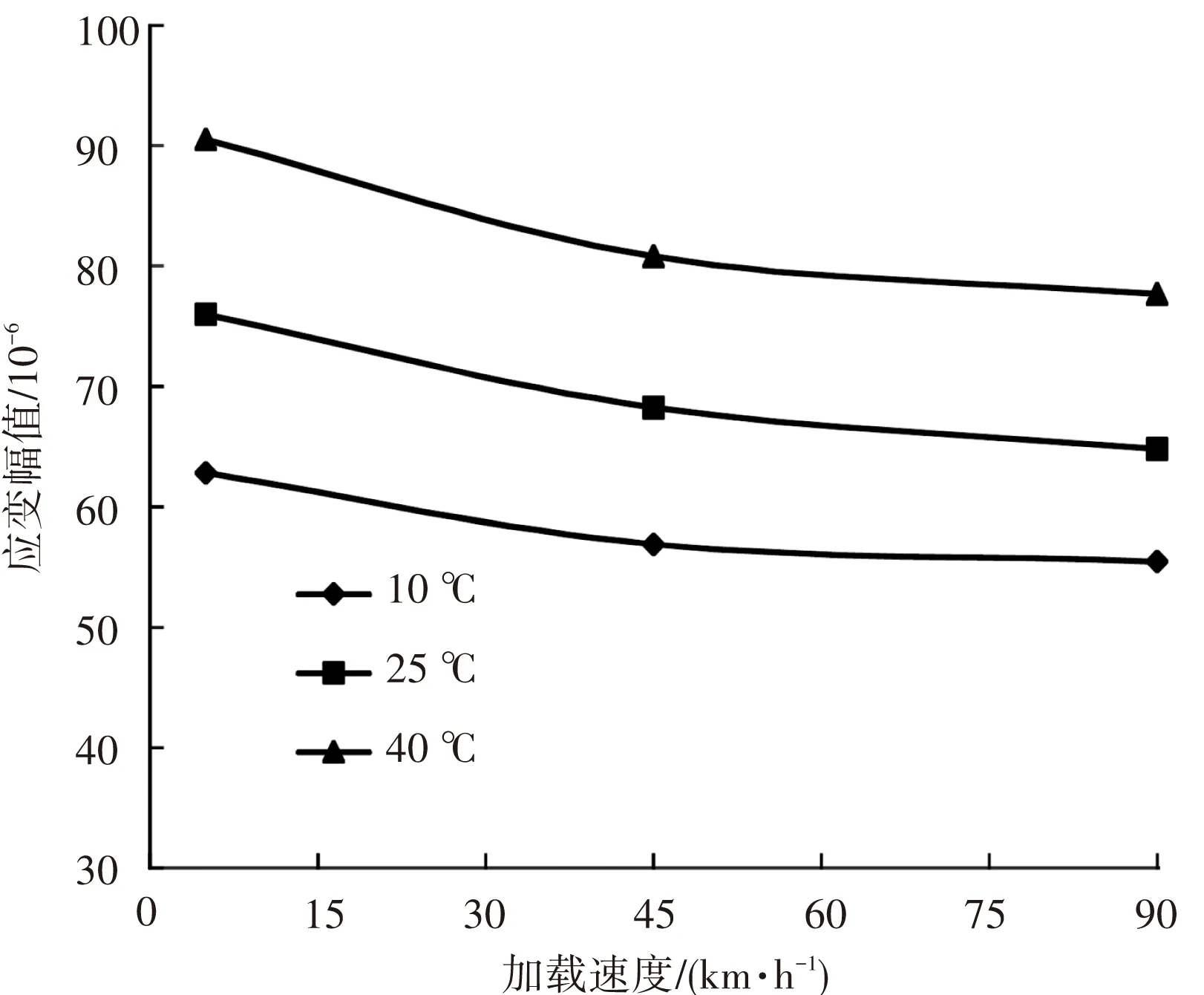
图18 水稳砂砾层底纵向应变幅值Fig.18 Longitudinal strain amplitude of water stabilized gravel bottom

图19 水稳砂砾层底横向应变幅值
Fig.19Transverse strain amplitude of water stabilized gravel bottom
图20为土基顶面压应力随温度和行车速度的变化,可见与水稳砂砾层底的情况类似,由于沥青层材料参数随温度和行车速度而变,土基顶面压应力随着温度增加或行车速度减小而增加,但增加的幅度较沥青层底力学响应不明显.

图20 土基顶面压应力幅值
5 结 论
1)通过辽宁省沥青路面足尺加速加载试验,对路面结构力学仿真方法和内部力学特性进行研究,排除了假定参数的影响,利用实测参数建立路面结构力学仿真模型. 所建立的模型能够较好地模拟路面结构不同位置处的力学响应,与光纤光栅传感器实测结果较为符合,可以用来进行路面结构受力特点的仿真分析.
2)计算值和实测值对比表明:在行车荷载作用下,沥青层底竖向受力呈现拉压交替变化;沥青层底水平受力为压—拉—压变化;半刚性基层层底以受拉为主;土基顶面承受压力作用. 由于荷载随深度扩散,随着结构深度的增加,力学响应曲线的持续时间增加.
3)沥青混合料粘弹特性导致的弹性后效使得沥青层的力学响应呈现非对称分布特点;而基层和路基处于弹性状态,其力学响应曲线形状不受沥青层粘弹性的影响,但峰值随加载速度的减小而增大.
4)路面结构内部力学响应受温度和加载速度的影响较大. 随着温度的增加和加载速度的减小,沥青层三向应变、半刚性基层底的水平应变以及土基顶面压应力的响应幅值增加,并且当温度较高或加载速度较低时,力学响应增加的效果更加明显.
[1] 姚祖康.对我国沥青路面现行设计指标的评述[J].公路, 2003(2):43-49.
YAO Zukang. A review on design criteria of asphalt pavements[J].Highway, 2003 (2):43-49.
[2] 孙立军.沥青路面结构行为理论[M].上海:同济大学出版社, 2003.SUN Lijun. Structural behavior study for asphalt pavement[M]. Shanghai: Tongji University Press,2003.
[3] 董泽蛟.多孔介质理论下饱水沥青路面动力响应分析[D].哈尔滨:哈尔滨工业大学,2006.
DONG Zejiao. Dynamic response analysis of saturated asphalt pavement based on porous medium theory[D]. Harbin:Harbin Institute of Technology,2006.
[4] 侯芸,郭忠印,田波,等. 动荷作用下沥青路面结构的变形响应分析[J]. 中国公路学报, 2002, 15(3): 6-10.
HOU Yun, GUO Zhongyin, TIAN Bo, et al. Dynamic deflection response of layered pavement structure subjected to dynamic load[J]. China Journal of Highway and Transport, 2002, 15(3): 6-10.
[5] 舒富民, 钱振东. 移动荷载作用下沥青路面的动力响应分析[J]. 交通运输工程与信息学报, 2007, 5(3): 90-95.
SHU Fumin, QIAN Zhendong. Analysis on the dynamic response of asphalt pavement under moving load[J]. Journal of Transportation Engineering and Information, 2007, 5(3): 90-95.
[6] 董泽蛟,曹丽萍,谭忆秋,等. 移动荷载作用下沥青路面三向应变动力响应模拟分析[J].土木工程学报,2009, 42(4): 133-139.DONG Zejiao, CAO Liping, TAN Yiqiu, et al. Analysis of the dynamic response of three directional strains in asphalt pavement under moving vehicle loads[J].China Civil Engineering Journal, 2009,42(4):133-139.[7] 刘宁. 半刚性基层长寿命路面力学响应的现场测试与分析[D]. 哈尔滨:哈尔滨工业大学,2012.
LIU Ning, Field test and analysis on mechanical response of semi-rigid base of long-life asphalt pavement[D]. Harbin: Harbin Institute of Technology,2012.
[8] 关宏信, 郑健龙, 张起森. 行车荷载作用下沥青路面粘弹性应力响应规律分析[J]. 中外公路, 2006, 26(1): 44-47.
GUAN Hongxin, ZHENG Jianlong, ZHANG Qisen.Analysis of viscoelastic stress response law of asphalt pavement under vehicle load[J]. Journal of China & Foreign Highway, 2006, 26(1): 44-47.
[9] 赵延庆,黄大喜,潘友强.柔性基层沥青路面结构黏弹性力学响应分析[J].土木工程学报,2007,40(5):96-99,110.
ZHAO Yanqing, HUANG Daxi, PAN Youqiang. Analysis of viscoelastic r esponses of asphalt pavements with flexible bases[J]. China Civil Engineering Journal, 2007,40(5):96-99,110.
[10]何兆益, 雷婷, 陈洪兴, 等. 沥青路面车辙变形的三维粘弹性动力有限元分析[J]. 重庆建筑大学学报, 2008, 30(6):33-34.
HE Zhaoyi , LEI Ting, CHEN Hongxing, et al. A 3D visco-elasto-plastic finite element analysis of the asphalt pavement rutting deformation[J]. Journal of Chongqing Jianzhu University, 2008, 30(6):33-34.
[11]赵延庆, 刘慧, 白龙, 等. 沥青混合料本构关系对路面力学响应的影响[J]. 中国公路学报, 2012, 25(5): 6-11.
ZHAO Yanqing, LIU Hui, BAI Long, et al. Effect of constitutive relationship of asphalt mixture on pavement response[J]. China Journal of Highway and Transport, 2012, 25(5): 6-11.
[12]张肖宁. 实验粘弹原理[M].哈尔滨: 哈尔滨船舶工程学院出版杜, 1990.
ZHANG Xiaoning. The experimental principle of viscoelastic[M]. Harbin:Harbin Engineering University Press,1990.
[13]PARK S W, SCHAPERY R A. Methods of interconversion between linear viscoelastic material functions:a numerical method based on Prony series[J].International Journal of Solids and Structures,1999,36(11): 1653-1675.
[14]谢水友.轮胎接触压力对沥青路面结构的影响研究[D].西安:长安大学, 2003.
XIE Shuiyou. Effects of the tire/pavement contact pressure on asphalt pavement[D]. Xi’an: Chang’an University,2003.
[15]赵延庆,王志超,王国忠,等.移动荷载下沥青路面内应力脉冲的持续时间[J]. 交通运输工程学报, 2009, 9(6): 11-15.
ZHAO Yanqing, WANG Zhichao, WANG Guozhong, et al. Stress pulse durations in asphalt pavement under moving load[J]. Journal of Traffic and Transportation Engineering, 2009, 9(6): 11-15.
[16]田庚亮,董泽蛟,胡庆立,等. 光纤光栅传感器与沥青混合料协同变形分析[J]. 哈尔滨工业大学学报,2009,41(5): 73-76.
TIAN Gengliang, DONG Zejiao, HU Qingli, et al. Analysis of coordination between asphalt mixture and fiber bragg grating sensor[J]. Journal of Harbin Institute of Technology,2009,41(5):73-76.
[17]张彬,王钊,杨俊峰,等.土压力盒在工程应用中的误差分析[J]. 探矿工程: 岩土钻掘工程, 2005, 32(B09): 157-161.
ZHANG Bin, WANG Zhao,YANG Junfeng,et al. Error analysis of earth pressure cell in geotechnical engineering[J]. Exploration Engineering: Rock and Soil Drilling Engineering, 2005, 32(B09): 157-161.
(编辑魏希柱)
Mechanical response measurement and simulation of full scale asphalt pavement
ZHANG Huaizhi1,REN Junda1,JI Lun2,WANG Lei3
(1. Key Laboratory of Expressway Maintenance Technology Ministry of Communications, PRC(Transportation Research Institute of Liaoning Province), Shenyang 110015, China; 2. School of Transportation Science and Engineering, Harbin Institute of Technology,Harbin 150090, China; 3.Liaoning Provincial Department of Transportation Highway Administration, Shenyang 110005, China)
In order to explore the mechanical response of asphalt pavement under the vehicle load, researches on the mechanical simulation method and the characteristics of internal mechanical response of asphalt pavement were conducted based on the full-scale accelerated test of asphalt pavement in Liaoning, China. Fiber bragg grating sensors were utilized to measure the mechanical response of the surface course bottom, the base course bottom and the top surface of the subgrade respectively. Viscoelastic parameters of asphalt mixtures were obtained through uniaxial compression dynamic modulus testing. Elasticity moduli of the base and subgrade were back-calculated through the FWD deflection basin. The distribution of the contact surface between the tires and the pavement surface was also measured. The sensors were calibrated through uniaxial compression dynamic modulus and four-point bending dynamic modulus testing. Based on the measured input data, a mechanical simulation model of the pavement structure was developed with the finite element software, ABAQUS, in order to analyze the mechanical response of pavement structure under different loading positions and speeds, then a subsequent comparison was made between the measured and calculated mechanical response data. The results indicate that the developed model can reasonably simulate the three-dimensional responses of the asphalt layer, the longitudinal and lateral response of the bottom of semi-rigid base, as well as the compressive stress on the subgrade surface. The viscoelastic property of the asphalt mixture induces the elastic aftereffect which leads to the asymmetry of the mechanical response curve. Amplitudes of the asphalt layer three-dimensional responses, horizontal responses of the bottom layer of the semi-rigid base and compressive stresses of the subgrade surface are all raised with the increase of temperature and the decrease of loading speed.
pavement engineering; accelerated pavement testing; viscoelastic three-dimensional finite element; pavement mechanical response; simulation model
10.11918/j.issn.0367-6234.2016.09.008
2014-11-18
辽宁省交通科技项目(201507)
张怀志(1982—),男,博士,高级工程师
任俊达,renjunda89@163.com.
U414.1
A
0367-6234(2016)09-0041-08
