例谈“超级画板”在数学探究性教学中的应用
2016-10-28郑义
郑 义
(福建省厦门双十中学,厦门 361001)
例谈“超级画板”在数学探究性教学中的应用
郑义
(福建省厦门双十中学,厦门361001)
数学课程的设计与实施应重视运用现代信息技术.“超级画板”作为我国自主研发的数学软件,为数学教学、数学学习及数学研究提供了一个新的平台和视野.
超级画板探究性教学
《义务教育数学课程标准(2011年版)》提出:“数学课程的设计与实施应重视运用现代信息技术,特别要充分考虑计算器、计算机对数学学习内容和方式的影响,大力开发并向学生提供更为丰富的学习资源,把现代信息技术作为学生学习数学和解决问题的强有力的工具,致力于改变学生的学习方式,使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去.”
“超级画板”作为我国自主研发的数学软件,是基于动态几何设计的智能教育平台,功能相当完善,为数学教学、数学学习及数学研究提供了一个新的平台和视野.本文将通过两个教学案例,体现“超级画板”在数学探究性教学中的应用.

【问题思考】这道题目本身并不难,我们固然可以通过分析该方程得出结论.但是这样处理的话,能否向学生解释清楚,能否让学生理解透彻,都是不确定的,再说也不利于学生进行积极地思考.如果我们利用“超级画板”来辅助教学,利用其动画及跟踪效果,在学生眼见为实的基础上得出相应结论,并引导学生根据观察结果进行严格地证明,那么课堂的探究性就更加明显了.
【问题处理】在“超级画板”辅助教学下,我们不妨先来研究下面几个问题.
(1)当l=0时,方程表示什么图形?
(2)当l取定值l0时,该方程表示什么图形?还是一条直线吗?
(3)当l变化时,该方程表示什么图形?该图形有什么特征?
教师提出问题后,先让学生思考.第(1)(2)问,学生不难回答:(1)当l=0时,方程表示直线l1.(2)可将方程化为:(3+2l)x+(4+l)y+(2l-2)=0,注意到x,y前面的系数3+2l、4+l不同时为零,因此当l取定值(不管该定值为何值)时,方程均为直线的方程,都表示一条直线.

图1
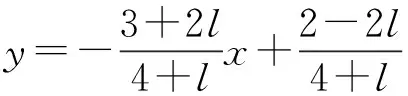
由图1,通过“超级画板”的演示,随着参数l的变化,学生可以观察到很多条直线.而这些直线有个共同特征:都经过了一个点,且这个点就是直线l1,l2的交点.由此可以引导学生粗略地得出结论:当l变化时,该方程表示经过点N的“很多条直线”,而确定一条直线的要素有定点和斜率.定点我们已经找到了,即两直线的交点,余下我们只要求直线的斜率即可.
【设计意图】 在本次探究中,教师将一个问题细分为三个小问题,并且层层递进,以一个引导者的身份,引导学生自己去思考探究,并且利用“超级画板”将变量l对方程的影响通过动态展现给学生,既给予了学生直观的印象,又活跃了课堂气氛,同时将问题化难为易.此过程虽然占用了课堂较多的时间,却将探究问题、思维发展的过程完完整整地呈现了出来,这样既激发了学生学习数学的兴趣,又提高了他们的数学探究能力.
【问题思考】这道轨迹问题,如果直接求解的话,难度及计算量相对较大.如何在课堂的有限时间里进行有效的教学,是我们要去突破的一个问题.能否将这个复杂的问题简单化?是否可以先猜测该问题的结论,再去证明呢?


(1)

(2)
观察可得结论:所求点的轨迹是以原点为圆心,a为半径的圆.由“超级画板”探究所得到的“轨迹为圆”的结论,其实给了我们解决这道题的几何方法.如何证明这个结论呢?

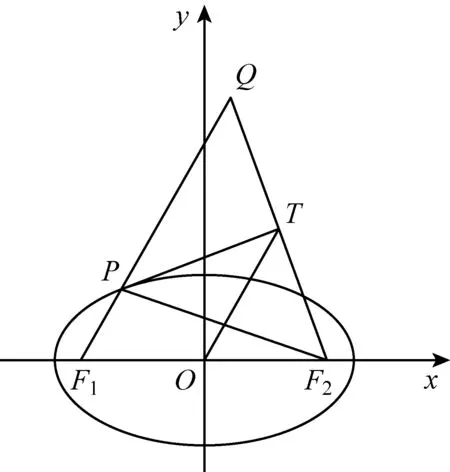
图3


所以PT⊥TF2,则PT为QF2的中垂线.故T为QF2的中点.
【设计意图】与传统的证明方法、探究方法相比,“超级画板”确实可以为数学问题的探究提供一个方便操作、方便学习、方便研究的途径.在一些几何命题的证明和探究上,“超级画板”在一定程度上避免了繁杂的计算过程、证明过程、逻辑推理过程,确实为学习和研究提供了一个便捷而准确,直观而深刻的渠道.
基于以上思考,在本次探究活动中,先利用“超级画板”探究所得到的“轨迹为圆”的结论,再证明动点到圆心的距离等于定值,化难为易.在探究过程中,引导学生从直观观察到严谨论证,较好地调动了学生的学习积极性,也体现了数学探究精神与课堂趣味性的有效结合.
《普通高中数学课程标准(实验)》提倡实现信息技术与课程内容的有机整合,注意把算法融入到数学课程的各个相关部分.提倡利用信息技术来呈现以往教学中难以呈现的课程内容,尽可能使用科学型计算器,各种数学教育技术平台,加强数学教学与信息技术的结合.鼓励学生运用计算机、计算器等进行探索和发现.把现代信息技术作为学生学习数学和解决问题的强有力的工具,致力于改变学生的学习方式,使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去.
“超级画板”确实在一定程度上有利于数学的教与学.有趣活泼的动画效果,生动直观的彩色图形,正是学习的最佳刺激.以趣引思,能使学生处于兴奋状态和积极思考状态,学生在这种情境下会乐于学习,也有利于对新知的吸收和理解,而这一切都是传统教学很难做到的.不过,凡事都有利弊,如何正确使用“超级画板”,使之更好地服务于数学教学,是值得我们继续思考和研究的.
[1]中华人民共和国教育部. 义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2]中华人民共和国教育部. 普通高中数学课程标准(实验)[S].北京:人民教育出版社,2003.
[3]张景中,彭翕成.数学教育技术[M].北京:高等教育出版社,2009.
(责任编辑:李珺)
