基于Maxwell-Stefan双扩散模型的煤层气注气数值模拟

孙晓飞, 张艳玉, 李　凯, 李志涛, 尚凡杰, 孙仁远

(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石油大学地球科学与技术学院,山东青岛 266580;3.中国石油新疆油田分公司实验检测研究院,新疆克拉玛依 834000; 4.中海油研究总院开发研究院,北京 100027)



基于Maxwell-Stefan双扩散模型的煤层气注气数值模拟

孙晓飞1,2, 张艳玉1, 李凯3, 李志涛1, 尚凡杰4, 孙仁远1

(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石油大学地球科学与技术学院,山东青岛 266580;3.中国石油新疆油田分公司实验检测研究院,新疆克拉玛依 834000; 4.中海油研究总院开发研究院,北京 100027)

目前煤层气注气数值模拟软件中均以扩展Langmuir模型模拟多组分气体吸附/解吸,以拟稳态单孔扩散模型和Fick定律描述煤层基质中气体扩散,虽然简单,便于应用,但存在较大局限性。以试验数据为依据,评价扩展Langmuir、IAS和2D PR-EOS多组分气体吸附模型可靠性,并建立Maxwell-Stefan双扩散模型模拟气体扩散过程。最后,将双扩散模型与煤储层气水两相多组分渗流模型耦合,利用IMPES方法求解研究煤层气注气过程。研究表明:2D PR-EOS模型预测结果优于扩展Langmuir和IAS模型;注气初期基质中多组分气体吸附和甲烷解吸速率较快,之后逐渐变缓;该模拟方法可以较为准确地模拟煤层气衰竭和注气开发过程,预测煤基质中气体各组分浓度分布,为煤层气注气开发的研究及现场应用提供有效的技术手段。

煤层气; 注气; 多组分吸附; 双扩散模型; Maxwell-Stefan方程

引用格式：孙晓飞，张艳玉，李凯，等. 基于Maxwell-Stefan双扩散模型的煤层气注气数值模拟[J].中国石油大学学报(自然科学版)，2016,40(3)：113-120.

SUN Xiaofei， ZHANG Yanyu， LI Kai， et al. Numerical simulation of gas injection enhanced coalbed methane recovery based on bi-dispersing diffusion model with Maxwell-Stefan equation[J].Journal of China University of Petroleum(Edition of Natural Science)，2016,40(3)：113-120.

由于二氧化碳、烟道气等气体能够通过竞争吸附置换煤储层孔隙内的甲烷,注气提高煤层气采收率技术逐渐成为国内外专家学者研究的热点[1-4]。煤层气注气过程涉及多组分气体的吸附/解吸、煤基质扩散以及割理中气水两相渗流等多个复杂问题，数值模拟技术是研究上述过程的重要手段[5-6]。现有煤层气注气模拟方法多采用扩展Langmuir模型描述多组分气体吸附,拟稳态单孔扩散模型表征煤基质微孔隙结构,Fick定律模拟气体扩散运动,不能真实反映煤层气注气过程[3,7-9]。笔者在评价多组分气体吸附模型的基础上,以Maxwell-Stefan双扩散模型描述气体二级扩散过程,建立基质割理气水流动耦合渗流方程,模拟煤层气注气开发过程,为煤层气注气开发的研究及现场应用提供有效的技术手段。

1　多组分气体吸附模型对比分析

煤层气注气数值模拟中亟待解决的一个关键问题是精确预测多组分气体(CO2、N2等)在煤层中的吸附/解吸过程[10]。目前煤层气模拟软件中均采用扩展Langmuir模型,该模型的假设条件与真实情况不符,尤其对于气体物性差异较大的多组分气体,预测精度更低。有必要筛选更为可靠的多组分气体吸附模型用于后续的煤层气注气数值模拟研究。本文中选取理想吸附溶剂模型(IAS)[11]和二维状态方程模型(2D PR-EOS)[12]与扩展Langmuir模型进行对比,确定每种模型的应用条件以及精度范围。

对于IAS模型,当吸附相为理想状态时,气相和吸附相平衡关系式的简化形式为

xipoi(Πi)=pyi.

(1)

式中,poi为组分i的蒸汽压,MPa;xi为吸附相中组分i的摩尔分数;Πi为组分i的扩展压力减少量。实际的吸附相扩展压不能直接测得,采用的计算式为

(2)

式中,πi为组分i的扩展压,MPa;A为吸附相的比表面积,m2/kg;MPa;T为温度,K;R为摩尔气体常数;ni(pi)为纯组分气体吸附等温式,为了避免数值积分运算,采用Langmuir等温式。由于在达到吸附平衡时各组分的扩展压力减少量相等,因此在给定p和yi初始值的情况下,根据式(1)和(2)以及约束条件(x1+x2+…+xnc=1)可以对nc+1个未知量进行迭代求解。

2D PR-EOS模型为

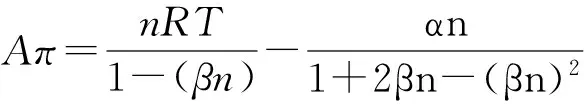
(3)

式中,n为单位质量吸附剂吸附的气体摩尔数,mol/kg;α和β为模型参数。

当吸附达到平衡时,满足:

Zaniφai=kifgi

(4)

式中,φai和fgi分别为组分i在气相中的逸度和吸附相中的逸度系数;ki为压力很低时吸附量和压力的比值;Za为与理想气体类似的吸附相压缩因子。对于nc个组分的混合气体,式(4)可以写出含有nc+1个未知量的方程组,加入约束条件(x1+x2+…+xnc=1)后,以扩展Langmuir模型的计算结果为迭代初始值,通过拟牛顿-拉夫森数值迭代算法可对其进行求解。

在预测多组分气体吸附量之前,需要确定Langmuir模型中的n和b以及2D PR-EOS模型的α、β和lnk等参数。国内外专家针对Fruitland煤进行了大量纯组分(CH4、CO2、N2)和多组分气体等温吸附试验,试验数据相对丰富、全面[13-14],因此本文中以46 ℃下气体在Fruitland湿煤和干活性炭上的等温吸附试验数据为依据[13],通过Langmuir和2D PR-EOS模型拟合试验数据确定上述参数,并通过RMSE(均平方根误差)表征拟合精度。等温吸附试验数据及拟合后的Langmuir和2D PR-EOS模型预测结果见图1,拟合后的模型参数见表1。由图1和表1可知,两种模型对甲烷和氮气的拟合精度明显高于二氧化碳,且2D PR-EOS模型拟合精度高于Langmuir模型。

以表1所示参数为基础,通过扩展Langmuir、IAS和2D PR-EOS模型分别对混合气体(CH4和CO2)在Fruitland湿煤和活性炭中的吸附进行计算,并与实际的试验数据进行对比,甲烷和二氧化碳混合气体在不同供给气组分下(由上至下甲烷摩尔分数分别为0.8、0.6、0.4、0.2)在Fruitland湿煤(温度45.85 ℃)和干活性炭(温度54.45 ℃)的甲烷吸附量如图2所示。

图1　纯组分等温吸附试验数据及模型预测结果Fig.1　Comparison of experimental data and predicted results of Langmuir and 2D PR-EOS models

纯组分气体Langmuir模型nL/(mol·kg-1)b/MPa-1RMSM2DPR-EOS模型α/(kg·mol-1)β/(kg·mol-1)ln(k/mol·kg-1·MPa-1)RMSECH4湿煤1.1370.2660.015-16970.3396-0.8440.006干活性炭6.1580.6690.115-2520.09401.9410.073CO2湿煤1.5440.6420.035-19990.09670.5320.027干活性炭9.3641.0600.165-2700.05323.0070.170N2湿煤0.9420.8970.009-20580.1863-2.3090.007干活性炭4.8600.3280.049-1370.12290.7310.019

图2　干活性炭和湿煤的甲烷吸附量预测结果Fig.2　Predicted results of amount of CH4 adsorption on Fruitland wet coal and dry activated carbon

由图2可知,2D PR-EOS模型相比其他模型更能适合高压系统的吸附预测。此外,对于Fruitland湿煤,扩展Langmuir、IAS和2D PR-EOS模型平均绝对偏差分别为10.96%、17.49%和6.00%。对于干活性炭,三者分别为21.59%、12.07%和4.85%。由此可知,IAS-Langmuir和扩展Langmuir模型对于不同煤的预测精度偏差较大,2D PR-EOS模型预测精度明显高于扩展Langmuir和IAS模型。其原因在于扩展Langmuir模型中,不同气体的饱和吸附量往往存在较大差异,这与热力学连续性不符合,且该模型未考虑气体相对吸附性随平衡气相组分和压力的变化,因此预测精度低于IAS和2D PR-EOS模型。IAS模型中将气相和吸附相分别看成理想气体和理想混合物,2D PR-EOS模型则基于实际气体和理想混合物,因此当压力较高时,IAS模型预测精度低于2D PR-EOS模型。

通过计算分离因子进一步对比3种模型在预测多组分吸附方面的差异,分离因子可以表征吸附剂对混合气体的相对吸附,对于两种组分(组分1和组分2)的吸附系统,分离因子的定义式为α=(x/y)1/(x/y)2[15]。3种模型计算所得干活性炭及Fruitland湿煤分离因子如图3所示。

图3　干活性炭及湿煤分离因子Fig.3　Separation factor on dry activated carbon and Fruitland wet coal

由图3可知,3种模型分离因子变化规律差异较大,扩展Langmuir模型的分离因子在整个吸附过程中为常数。IAS模型在平衡气相浓度一定时,预测的分离因子随压力增加而降低。同一压力下,分离因子与平衡气相组分成正比。2DPR-EOS模型在煤吸附性较强时,表现出与IAS模型相同的规律,当煤的吸附性降低时,分离因子的变化规律与IAS模型截然相反。此外,对于IAS和2DPR-EOS两种模型,低压下,气相组分对分离因子的影响较小,随压力增大,气相组分的影响效果增加。原因在于IAS和2DPR-EOS模型考虑了吸附过程中气体相对吸附性随组分和压力的变化,而扩展Langmuir模型没有考虑该因素。由此可知,在预测多组分竞争吸附方面,IAS和2DPR-EOS模型相比于扩展Langmuir更具有优势。综上所述,2DPR-EOS模型优于扩展Langmuir和IAS模型。

2　基于Maxwell-Stefan的基质双扩散模型

假设煤基质由多个割理系统包围的圆柱形单元组成(图4),每个单元体充填等半径的球形颗粒,颗粒内部包含着等半径球形微颗粒。球形微颗粒之间的空隙为基质大孔隙,气体以自由相存在,微颗粒内为基质微孔隙,只存在吸附相气体。气体在基质中的扩散为二级扩散,基质大孔隙中气体扩散受分子扩散和努森扩散控制,基质微孔隙中主要为吸附相气体的表面扩散。扩散过程中整个系统等温,且煤基质中不考虑水相的存在。

图4　双扩散孔隙结构示意图Fig.4　Conceptual model for bidisperse pore structure

根据以上假设,基质大孔隙里气体的流动可简化为一维达西流,物质平衡方程式为

(5)

式中,φc为基质大孔孔隙度;Cci为基质大孔隙中气体组分i的摩尔浓度;ug为气体速度;Jm-c为单位体积基质大孔隙与球形颗粒之间的交换量。

对于半径为Rp的球形颗粒,采用考虑分子扩散和努森扩散的Maxwell-Stefan方程描述多组分气体在基质微孔隙中的扩散过程[16],满足:

(6)

初始条件和边界条件为

式中,φm为基质微孔孔隙度;Cmi和Cmj为基质微孔隙中气体组分i、j的摩尔浓度,mol/m3;Dmij为考虑气体组分i和j相互作用的扩散系数;Jm-μ为单位体积基质颗粒中,微孔和大孔之间气相组分i的交换量;Cm0i和Cci分别为基质微孔隙和大孔隙中气体组分i的原始气体摩尔浓度,mol/m3。

对于半径为rμ的微球形颗粒,建立气体组分i在微孔隙中扩散的物质平衡方程,并将描述表面扩散的Maxwell-Stefan方程代入,得

(7)

初始条件和边界条件为

Cμi=CEi(Cm).

式中,φμ为球形微颗粒孔隙度;Cμi为微颗粒中,吸附相气体组分i的气体摩尔浓度;CEi为基质微颗粒表面达到吸附平衡时气体组分i的摩尔浓度,通过优选的2D PR-EOS多组分吸附平衡模型计算;Cμ0i为基质微颗粒气体组分i的原始摩尔浓度。

式(5)～(7)加上相应的初始条件和边界条件构成了基于Maxwell-Stefan方程的基质双扩散模型。该模型通过数值方法进行求解。首先引入无因次参数(无因次浓度、无因次半径等),之后采用有限差分方法进行求解。其中,考虑到在基质颗粒的边界处气体浓度的变化大于颗粒球心处,差分过程采用等比级数网格进行差分。由于采用以上优选的非线性2D PR-EOS多组分吸附模型,使方程组的求解过程需对平衡吸附量进行半隐式处理。

3　煤层气注气数值模拟

3.1多组分渗流数学模型

假设煤储层是由割理系统和基质系统构成,煤基质为图4所示的双孔隙结构;储层具有非均质,各向异性,可压缩,生产过程中上覆岩层压力保持不变;割理系统中,气水两相的流动符合达西渗流定律,并考虑重力和毛管力的影响;多组分气体在煤基质中为双扩散过程,服从Maxwell-Stefan扩散运动方程。割理中气体为自由气体,服从真实气体状态方程,液体微可压缩,并考虑了气体在水中的溶解;初始条件下,煤储层割理中只有水相,基质大孔隙和微孔隙中不考虑水相的存在。

(1)割理系统气水两相渗流方程。割理系统中气相组分i及水相渗流方程分别为

(8)

(9)

式中,k为割理系统的绝对渗透率,10-3μm2;Krg和Krw分别为割理中气、水相对渗透率;μg和μw分别为混合气相和水相黏度,mPa·s;Bg和Bw分别为混合气相和水相体积系数;pg和pw分别为割理系统中气相和水相的压力,MPa;D为标高,从某一基准面算起的垂直方向深度(海拔),m;Rswi为水相中气体i的溶解气水比;ρg和ρw分别为储层条件下混合气相和水相密度,kg/m3;φf为割理系统孔隙度;Sg和Sw分别为割理系统中混合气相和水相饱和度;yi为割理系统中气体组分i在气相中所占的摩尔分数;qgi和qw分别为地面标准条件下单位时间单位体积煤岩内产出或注入气相组分i的体积和产出或注入水的体积,m3/(m3·d);qsi为地面标准条件下单位时间单位体积煤岩中从煤基质吸附/解吸的气相组分i的体积,m3/(m3·d)。

(2)煤基质与割理之间窜流量计算。煤基质与割理之间窜流量的计算涉及到多组分气体在煤基质中的吸附/解吸和扩散两个过程,其值等于所求时刻基质中含气量与前一时刻基质中含气量的差值,其计算表达式为

(10)

模型中多组分气体的吸附平衡采用优选的2DPR-EOS多组分吸附模型。

(3)辅助方程。

饱和度方程为

Sw+So=1;

毛管力方程为

pcow=po-pw;

气体组分约束方程为

y1+y2+…+ync=1;

气体分压与总气相压力关系式为

pg=pg1+pg2+…+pgnc.

3.2模型求解及实例计算

模型的求解过程如下:

(1)多个气体组分i的渗流方程相加得到总的气相渗流方程,并通过辅助方程消去Sw和Sg两个未知量,从而使其只有未知量pw。

(2)通过块中心差分对方程离散。差分过程中传导系数、毛管压力、产量项以及扩散项采用显式处理,对压力采用隐式处理,最后得到一个七对角矩阵。该过程中相对渗透率和气相摩尔分数取上游权,流体体积系数取算术平均,传导系数取调和平均。混合气体压缩因子采用DPR方法,溶解气水比由单组分溶解气水比叠加,黏度由Herning等[17]提出的混合方法计算。

(3)求解差分方程组。首先,采用预处理共轭梯度法求解,得到n+1时刻水相压力pw,把时间步长分成m段,依次计算每一小时间段的气水饱和度、CEi、xi及yi。每次求出饱和度之后都需要重新计算与饱和度有关的系数值(Krg等),然后再求下一小时间步的饱和度,依次类推。

以一个400m×400m×5m的5点井网区块为例研究注气过程,模拟计算储层和流体参数:网格尺寸为21×21×1,煤层顶深为500m,煤层原始含水饱和度为1.0,煤层原始压力为5.0MPa,割理孔隙度为5.0%,割理渗透率为5.0×10-3μm2,割理压缩系数为0.03MPa-1,基质压缩系数为0.03MPa-1。基质双扩散模型参数:基质大孔孔隙度为0.000 1,基质微孔孔隙度为0.001,扩散速率比值为0.01,储容比ω为500,煤密度为1.35g/cm3,基质颗粒半径为0.05m,初始大孔扩散系数为3.0×10-9m2/s,初始微孔扩散系数为5.0×10-13m2/s。基质双扩散模型采用的扩散系数见表2。

表2　基质双扩散模型扩散系数

生产控制条件为生产初期煤层气井排水降压开发,生产至2 000 d时,模型四角注气井向煤层注入不同摩尔分数的CO2和N2混合气体,注入压力和注入量分别为20 MPa和500 m3/d,中心一口生产井的井底流压为0.2 MPa。

计算结果见图5。由图5可得:①衰竭式开发过程中产气量曲线出现双峰值,符合煤层气衰竭开发特征,验证了模型的正确性;②随着混合气体中CO2摩尔分数的增加,日产气量不断增加,注入纯CO2时,煤层气日产量最高,累积产量最大为6.507 2×106m3,采出程度较衰竭式开发提高6.1%。由此可见,注CO2提高煤层气采收率效果好于注N2。

图5　不同摩尔分数CO2和N2混合气体日产气量Fig.5　Comparison of gas production rates under different gas injection components

以图5中CO2与N2摩尔分数比为1∶1的模拟结果为例,分析基质大孔隙和微孔隙中CH4、CO2和N2浓度随时间和空间的变化情况(图6)。由图6可知:① 随时间和距离的增加,基质大孔隙和微孔隙中CH4含量逐渐降低,CO2和N2浓度逐渐增加,表明CO2和N2可以通过竞争吸附置换CH4,且越接近基质表面,吸附量越大;② 基质大孔隙中,CO2的总体浓度低于N2(图6(b)和(c)),并且只存在于基质表面附近,而在基质微孔隙中,边界附近的CO2含量远大于N2含量,并随着颗粒半径的减小迅速降低,在半径值较小处,N2的含量高于CO2含量(图6(e)和(f)),由此可知,由于煤对CO2具有较强吸附性,导致CO2的扩散距离短,主要集中在煤基质表面处,相比之下,N2的扩散距离远,能够驱替出煤基质深处的煤层气。

煤基质中CH4、CO2浓度分布如图7所示。由图7可知,由于CH4在注入气的驱替作用下向生产井周围聚集,使生产井周围CH4浓度较高;由于注入气的影响,注入井周围CO2浓度高于生产井周围。煤基质中CH4、CO2和N2吸附/解吸速率随时间变化如图8所示。由图8可知,注气初期CH4解吸、CO2和N2吸附速率较大,之后逐渐变慢,且基质中CO2吸附速率明显高于N2。

图6　基质大孔隙、微孔隙中CH4、CO2和N2无因次浓度随时间和空间的变化规律Fig.6　Dimensionless concentration distribution of CH4, CO2 and N2 as a function of space and time in macropore and micropore

图7　煤基质中CH4、CO2浓度分布Fig.7　Concentration distribution of CH4 and CO2 in matrix

图8　煤基质中CH4、CO2和N2吸附/解吸速率随时间变化Fig.8　Exchange rates of CH4, CO2 and N2between matrix and cleat

4　结　论

(1)对于纯组分气体的吸附计算,2D PR-EOS模型计算精度高于Langmuir模型,且两者对CH4的拟合精度高于CO2。对于混合气体的吸附计算,2D PR-EOS模型预测结果好于扩展Langmuir和IAS模型,且能体现多组分气体的相对吸附。

(2)与N2相比,煤对CO2具有较强吸附性,导致CO2扩散距离短,主要集中在煤基质表面,而N2的扩散距离远,能够驱替出煤基质深处的煤层气。注气初期基质中多组分气体吸附和甲烷解吸的速率较快,之后逐渐变缓,基质中CO2吸附速率明显高于N2。

(3)基于Maxwell-Stefan双扩散模型的煤层气注气数值模拟方法可以准确地模拟煤层气衰竭和注气(CO2、N2、烟道气等)开发过程,预测煤基质中气体各组分浓度分布,为煤层气注气开发的研究及现场应用提供有效的技术手段。

[1]张松航,唐书恒,潘哲军,等.晋城无烟煤CO2-ECBM数值模拟研究[J].煤炭学报,2011,36(10):1741-1747.

ZHANG Songhang, TANG Shuheng, PAN Zhejun, et al. Numerical simulation of CO2enhanced coalbed methaneon Jincheng anthracite coal reservoir [J]. Journal of China Coal Society, 2011,36(10):1741-1747.

[2]刘冰,杜继芸,綦耀光,等.抽油机井杆管环空瞬态流场煤粉颗粒排出研究[J].中国石油大学学报(自然科学版),2014,38(1):117-123.

LIU Bing, DU Jiyun, QI Yaoguang, et al. Research on coal particle carrying out in unsteady flow field of rod pumped well annulus [J]. Journal of China University of Petroleum (Edition of Natural Science), 2014,38(1):117-123.

[3]LAW D H S, VAN L G H, GUNTER W D. Numerical simulator comparison study for enhanced coalbed methane recovery processes part I: pure carbon dioxide injection [R]. SPE 75669, 2002.

[4]叶建平,冯三利,范志强,等.沁水盆地南部注二氧化碳提高煤层气采收率微型先导性试验研究[J].石油学报,2007,28(4):77-80.

YE Jianping, FENG Sanli, FAN Zhiqiang, et al. Micro pilot test for enhanced coalbed methane recovery by injecting carbon dioxide in south part of Qinshui Basin[J]. Acta Petrolei Sinica, 2007,28(4):77-80.

[5]范铁刚,张广清. 注液速率及压裂液黏度对煤层水力裂缝形态的影响[J].中国石油大学学报(自然科学版),2014,38(4):117-123.

FAN Tiegang, ZHANG Guangqiang. Influence of injection rate and fracturing fluid viscosity on hydraulic fracture geometry in coal[J]. Journal of China University of Petroleum (Edition of Natural Science),2014,38(4):117-123.

[6]李明忠,陈会娟,张贤松,等. 煤层气多分支水平井井筒压力及入流量分布规律[J].中国石油大学学报(自然科学版),2014,38(1):92-97.

LI Mingzhong, CHEN Huijuan, ZHANG Xiansong, et al. Wellbore pressure and inflow rate distribution of multi-lateral horizontal well for coalbed methane [J]. Journal of China University of Petroleum (Edition of Natural Science), 2014,38(1):92-97.

[7]张芬娜,李明忠,綦耀光,等.煤层气排采产气通道适度携煤粉理论[J].中国石油大学学报(自然科学版),2015,39(2):86-91.

ZHANG Fenna, LI Mingzhong, QI Yaoguang, et al. Analysis of pulverized coal migration during CBM production [J]. Journal of China University of Petroleum (Edition of Natural Science), 2015,39(2):86-91.

[8]PILLALAMARRY M, HARPALANI S, LIU S. Gas diffusion behavior of coal and its impact on production from coalbed methane reservoirs [J]. International Journal of Coal Geology, 2011,86(4):342-348.

[9]YI J, AKKUTLT I Y, DEUTSCH C V. Gas transport in bidisperse coal particles: investigation for an effective diffusion coefficient in coalbeds [J]. Journal of Canadian Petroleum Technology, 2008,47(10):20-26.

[10]ZHENG G, PAN Z, TANG S, et al. Laboratory and modeling study on gas diffusion with pore structures in different-rank Chinese coals [J]. Energy, Exploration & Exploitation, 2013,31(6):859-878.[11]MYERS A L, PRAUSNITZ J M. Thermodynamics of mixed-gas adsorption[J]. AIChE Journal, 1965,11(1):121-127.

[12]ZHOU C, HALL F, GASEM K A M, et al. Predicting gas adsorption using two-dimensional equations of state [J]. Industrial & Engineering Chemistry Research, 1994,33(5):1280-1289.

[13]HALL F E, ZHOU C, GASEM K A M, et al. Adsorption of pure metnane,nitrogen,and carbon dioxide and their binary mixtures on wet Fruitland coal [R]. SPE 29194, 1994.

[14]SUDIBANDRIYO M, PAN Zhejun, FITZGERALD J E, et al. Adsorption of methane, nitrogen, carbon dioxide, and their binary mixtures on dry activated carbon at 318.2 K and pressures up to 13.6 MPa [J]. Langmuir,2003,19(13):5323-5331.

[15]CLARKSON C R, BUSTIN R M. Binary gas adsorption/desorption isotherms: effect of moisture and coal composition upon carbon dioxide selectivity over methane [J]. International Journal of Coal Geology, 2000,42(4):241-271.

[16]KRISHNA R, WESSELINGH J A. The Maxwell-Stefan approach to mass transfer [J]. Chemical Engineering Science, 1997,52(6):861-911.

[17]李士伦.天然气工程[M].北京:石油工业出版社,2009.

(编辑李志芬)

Numerical simulation of gas injection enhanced coalbed methane recovery based on bi-dispersing diffusion model with Maxwell-Stefan equation

SUN Xiaofei1,2， ZHANG Yanyu1， LI Kai3， LI Zhitao1, SHANG Fanjie4， SUN Renyuan1

(1.School of Petroleum Engineering in China University of Petroleum, Qingdao 266580, China;2.SchoolofGeosciencesinChinaUniversityofPetroleum,Qingdao266580,China;3.InstituteofExperimentandAnalysis,PetroChinaXinjiangOilfieldCompany,Karamay834000,China;4.DevelopmentResearchDepartment,CNOOCResearchInstitute,Beijing100027,China)

In most commercial coalbed methane simulation software, an extended Langmuir model, quasi-steady single pore diffusion and Ficks law are currently used to describe the adsorption of mixed gases on coal rocks and gas diffusion process. Although these methods are simple and easy for application, there are also some limitations. In this paper, the effectiveness of the extended Langmuir, IAS and 2D PR-EOS models for the prediction of the gas adsorption process on coal was analyzed with experimental data in order to establish a better model for the simulation. Then, the Maxwell-Stefan equation was used to develop a bi-dispersing diffusion model, in which the 2D PR-EOS model was used to predict multi-component gas adsorption. Finally, the bi-dispersing diffusion model was coupled with a gas/water two-phase multi-component simulation model, and the IMPES method was used to solve the equations. The simulation results of gas injection for enhanced coalbed methane recovery using CO2and N2show that the 2D PR-EOS model is better than the extended Langmuir and IAS models, which can reflect the relative adsorption of multi-component gases. The adsorption and desorption rates of gases are faster in the early stage of the gas injection, then gradually become slow, and the adsorption rate of CO2is significantly higher than that of N2. This numerical simulation method can effectively simulate the gas injection process for enhanced methane recovery, and accurately predict the distribution of different gas components in the coal matrix.

coalbed methane; gas injection; multi-component adsorption equilibrium; bi-dispersing diffusion model; Maxwell-Stefan equation

2015-09-25

国家科技重大专项(2009ZX05042-003);中国博士后科学基金面上项目(2015M582168);山东省自然科学基金项目(ZR2011EL034)

孙晓飞(1984-),男,博士,博士后,研究方向为煤层气数值模拟。E-mail:sunxiaofei540361@163.com。

1673-5005(2016)03-0113-08doi:10.3969/j.issn.1673-5005.2016.03.015

TE 357

A