仿蜻蜓扑翼飞行器机构设计及气动力研究

孙卫, 冯春鹏

(北方工业大学 机械与材料工程学院, 北京 100144)



仿蜻蜓扑翼飞行器机构设计及气动力研究

孙卫, 冯春鹏

(北方工业大学 机械与材料工程学院, 北京 100144)

针对蜻蜓扑翼飞行机理与鸟类单翼飞行机理的不同,设计了一种双翅翼空间四杆扑翼机构,提出了一种非对称刚度柔性翅翼。该翅翼上拍时刚度较小,下拍时刚度较大,上拍时翅翼变形比下拍时翅翼变形大,空气阻力较小,可以提高每个拍动周期中的等效升力,从而有效减小飞行器飞行时的能耗速度,提高飞行效率。基于非定常空气动力学原理,建立了仿蜻蜓扑翼飞行器的动力学模型,对双翼挥拍过程中不同相位差下的升阻特性进行了分析,可为飞行过程中扑动模式的选择提供参考。

双翅翼; 非对称刚度; 相位差

0　引言

扑翼飞行涵盖了固定翼飞行和旋翼飞行的优点,可以实现快速地起飞、加速和悬停,具有高度的机动性和灵活性。蜻蜓具有两对独立控制的翅翼,所以其空气动力学特性与大部分昆虫显著不同[1]。近年来,对于鸟类这种单翼飞行的升力机理已取得了相当的技术成果[2-4],但是对于蜻蜓这类双翅翼的飞行机理研究还处于初级阶段。

本文设计了一种双翅翼仿蜻蜓扑翼机构,实现了两对翅膀的协调运动,通过拍打具有相位差的翅翼实现了悬停飞行,依靠阻力产生足够的升力来支撑机体重量。针对以往翅膀在正反方向拍动时刚度相同、扑翼飞行器的飞行能效性很低的缺点,提出一种非对称刚度柔性平板翼,并进行了理论分析和有限元仿真。昆虫飞行的核心问题是如何产生高升力,在扑翼飞行机理研究的初级阶段,人们采用与固定翼飞行相同的模式来计算翅翼在稳态空气动力学环境下的升力。通过对果蝇翅翼的风洞实验表明,定常流产生的升力并不足以支撑果蝇自身的体重。因此,提出了非定常流空气动力学理论来解释扑翼飞行时产生的高升力机理。

1　扑翼机构原理

1.1传动机构设计

昆虫翼的运动有3个自由度[5]:挥拍角(φ)运动、迎角(α)运动和偏航角(ψ)运动。仿蜻蜓扑翼飞行器设计中,通过锂电池给直流电机供电,带动二级减速齿轮驱动空间曲柄摇杆机构使机翼上下扑动,产生挥拍角运动;通过舵机作用在前翅翼上使翅翼摆动,产生迎角运动。在蜻蜓的飞行过程中,偏航角较小,一般小于6°,所以为了简化飞行器模型,在悬停过程分析中可以将偏航角忽略。

在运动学分析中,不考虑力的作用,研究机构的相对位置和姿态情况,求解出各杆的相对位移、速度、加速度与主动件的关系,它是研究系统动力性能的必要条件。为了提高系统传动性能并且减少摩擦,避免机构中出现高副和移动副,采用的扑翼机构为空间曲柄摇杆机构,图1为仿蜻蜓扑翼飞行器前翼的传动机构简图和三维设计模型。

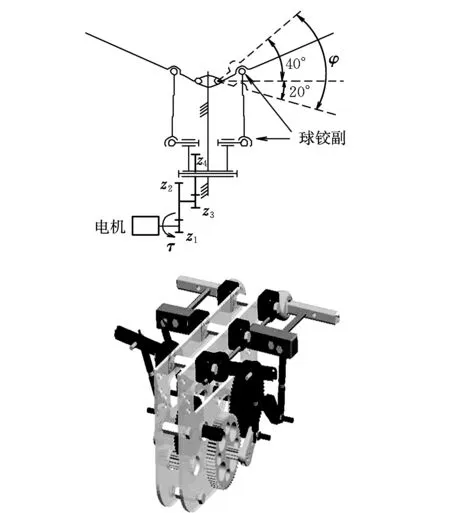
图1　扑翼传动机构简图和三维设计模型Fig.1　Transmission mechanism of the flapping-wing and 3-D design model

本文以北方工业大学研制的飞行器样机为研究对象,其电机到曲柄的传动比为:

(1)

式中:z2=50是模数为0.5的塑料齿轮;z1=11为固定在电机上的齿轮;z3=8为二级减速齿轮。齿轮z1和z4为铜齿轮,目的是为了提高其使用寿命。带动后翼拍打的齿轮和z4齿轮完全相同,所以前后翼齿轮的传动比为1∶1。

电机的最高转速ω=22 000 r/min,则翅翼的挥拍频率为:

(2)

利用ProE创建扑翼结构零部件,然后虚拟装配成整体的扑翼结构三维模型。利用ADAMS运动仿真模块进行简单的运动学分析,验证了机构设计的合理性,图2为加工装配成的实物图。

图2　双翅翼飞行器实物图Fig.2　Double-wing air vehicles prototype

所设计的前后翼拍打极限不一样,其水平位置也不对称,后翼的下拍极限为0°、上挥极限为60°,即挥拍角60°。前后翼拍动时会出现相位差,以前后翼相差1/2周期(反相)为例,其翅翼的简谐扑动方式如图3所示。

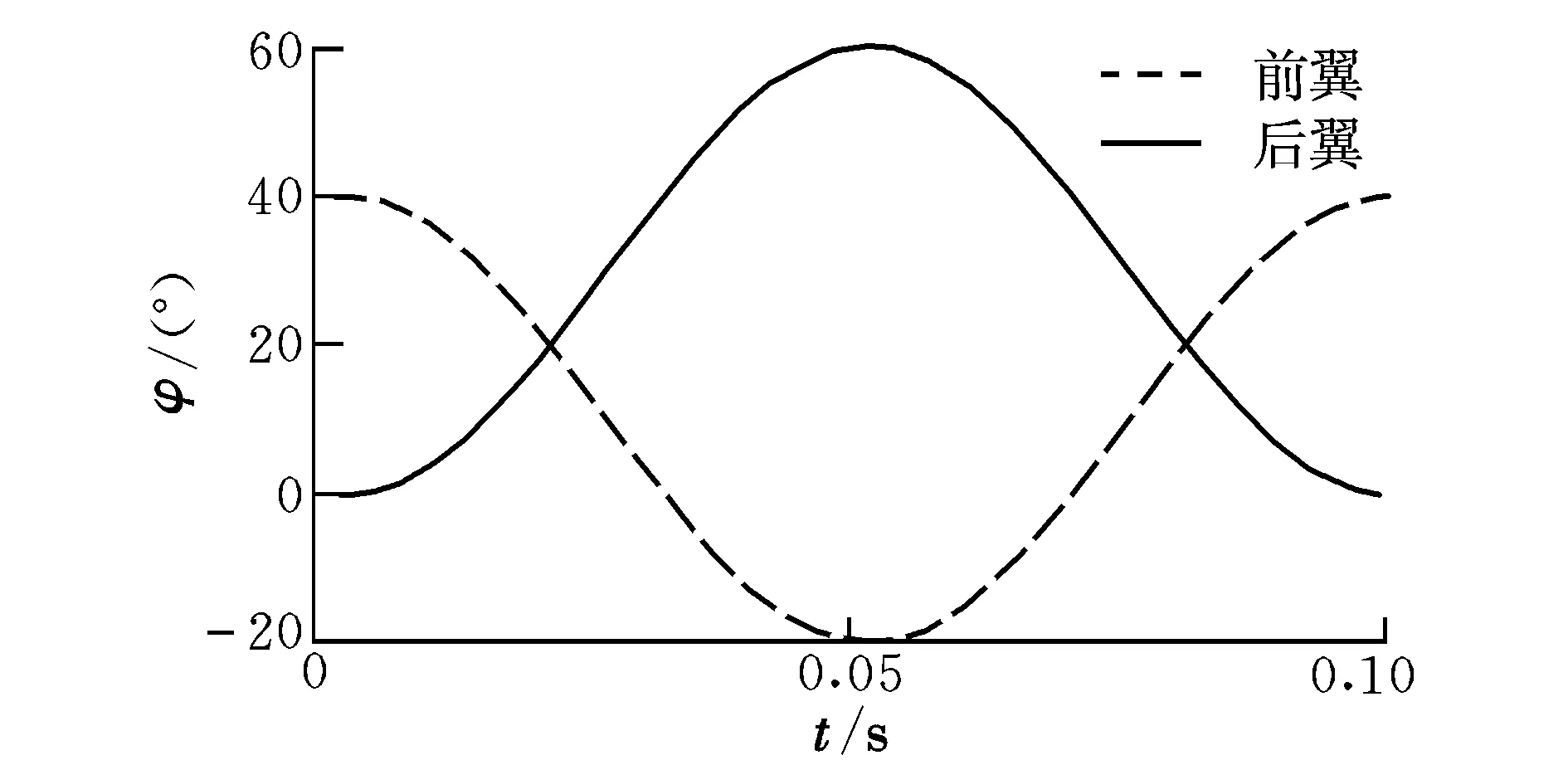
图3　前后翼扑翼角曲线Fig.3　Simulation of angle curves for flapping wings

1.2翅翼结构设计

小型鸟类高速拍动翅膀时,其翅膀的运动轨迹是由拍动和扭转运动复合而成。翅膀在上拍和下拍时,都会受到空气阻力。下拍时空气阻力做正功,上拍时空气阻力做负功。为了提高飞行能量效率,鸟类在机动飞行时,自然地在翅膀下拍时使迎风面积变大,上拍时迎风面积变小,从而提高飞行效率。以往的小型扑翼飞行器机构多采用柔性薄膜翅形[6-8],通过碳纤维杆作为翅膀骨架,其翅膀在正反两个方向拍动时刚度都相同,产生升力只能通过调整迎角和加快拍动频率以提高飞行速度来实现,使得扑翼飞行器的飞行能效性很低,多数小型扑翼飞行机器人只能连续飞行10 min左右。

本文的扑翼飞行器翅翼采用带有碳纤维骨架的柔性翼,翼膜材料为风筝布。由于其在扑动过程中会受到气动力和气动力矩的作用,因此会产生柔性变形,如图4所示。

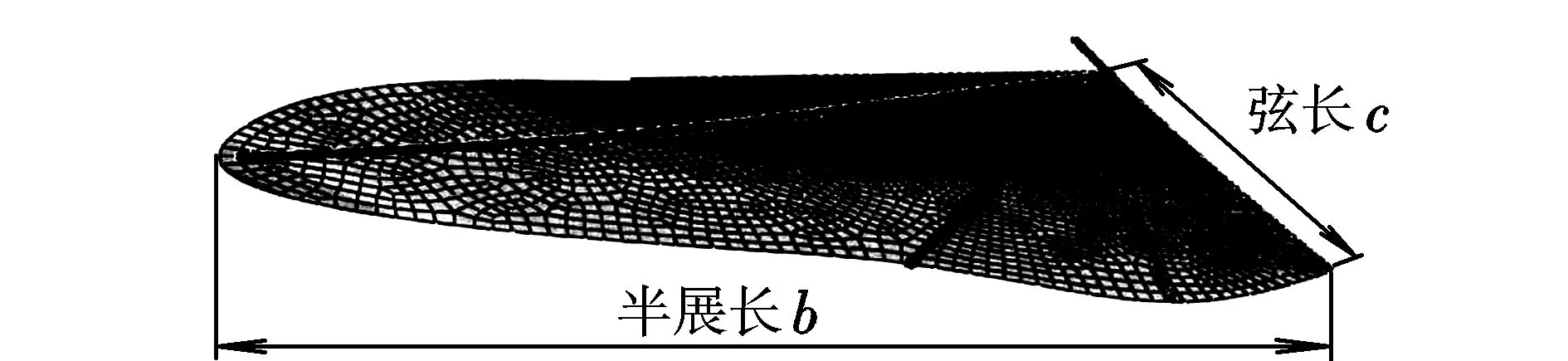
图4　翅翼的柔性变形Fig.4　Flapping-wing flexible deformation

扑翼受到的气动力矩可分解为展向弯曲力矩和弦向扭转力矩。弯曲力矩造成展向的柔性变形,扭转力矩造成弦向的柔性变形。由于柔性翼采用前缘刚性骨架,因此计算时取前缘处为扭转轴。翅翼扭转以抛物线规律变化,翼稍处扭转最大,翼根处不扭转,其弦向的扭转函数为:

(3)

式中:αt为翼尖扭转角;c为弦长;b为半展长。

扭转力矩与弦向柔性变形息息相关。αt和扭转力矩成正比,翅翼从最高点开始下拍时,扭转力矩逐渐增大。到达水平位置,也就是翅翼与垂直空气接触面积最大时扭转力矩最大,然后开始逐渐减小,到达下极限位置时最小,然后从最低点开始上拍时扭转力矩逐渐增大,到达水平位置时最大。αt的函数表达式为:

(4)

式中:αmax为翼尖最大柔性变形角。因此,弦向的扭转函数为:

(5)

气动弯曲力矩会造成展向的柔性变形,利用上述对弦向的柔性变形分析方法,可以得到展向的扭转函数为:

(6)

不考虑翅翼的柔性变形,翅翼只能进行上下拍动运动,其拍动函数为:

(7)

式中:α(t)为翅翼迎角;α为翅翼的固定迎角;β(t)为翼面与水平面的夹角;β0为翅翼的初始拍动角;β为拍动幅度;f为拍动频率。

综合上述分析,柔性翅翼的拍动函数为:

(8)

本设计采用非对称刚度柔性平板翼,即采用平行接触的柔性骨架结构,如图5和图6所示。通过设计使得柔性平板翼在上拍时刚度较小,下拍时刚度变大,这种非对称刚度柔性平板翼设计,可以提高每个拍动周期中的等效升力,从而有效减小飞行器飞行时的能耗速度,提高飞行效率。

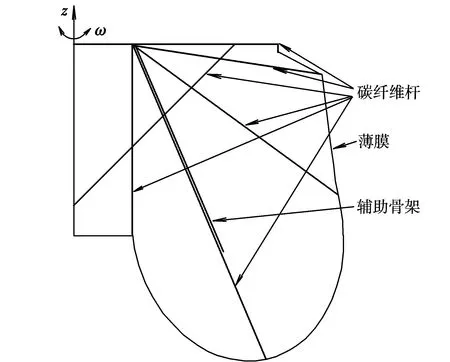
图5　非对称刚度柔性平板翼结构Fig.5　Structure of asymmetric stiffness flexible flat wing

图6　非对称刚度柔性平板翼Fig.6　Flexible flat wings with asymmetric stiffness

图7为上下拍动变形的有限元仿真分析示意图。根据图中位移数值可以看出:该非对称刚度柔性平板翼上拍时翅膀变形比下拍时翅膀变形大,验证了该结构设计的可行性和合理性。

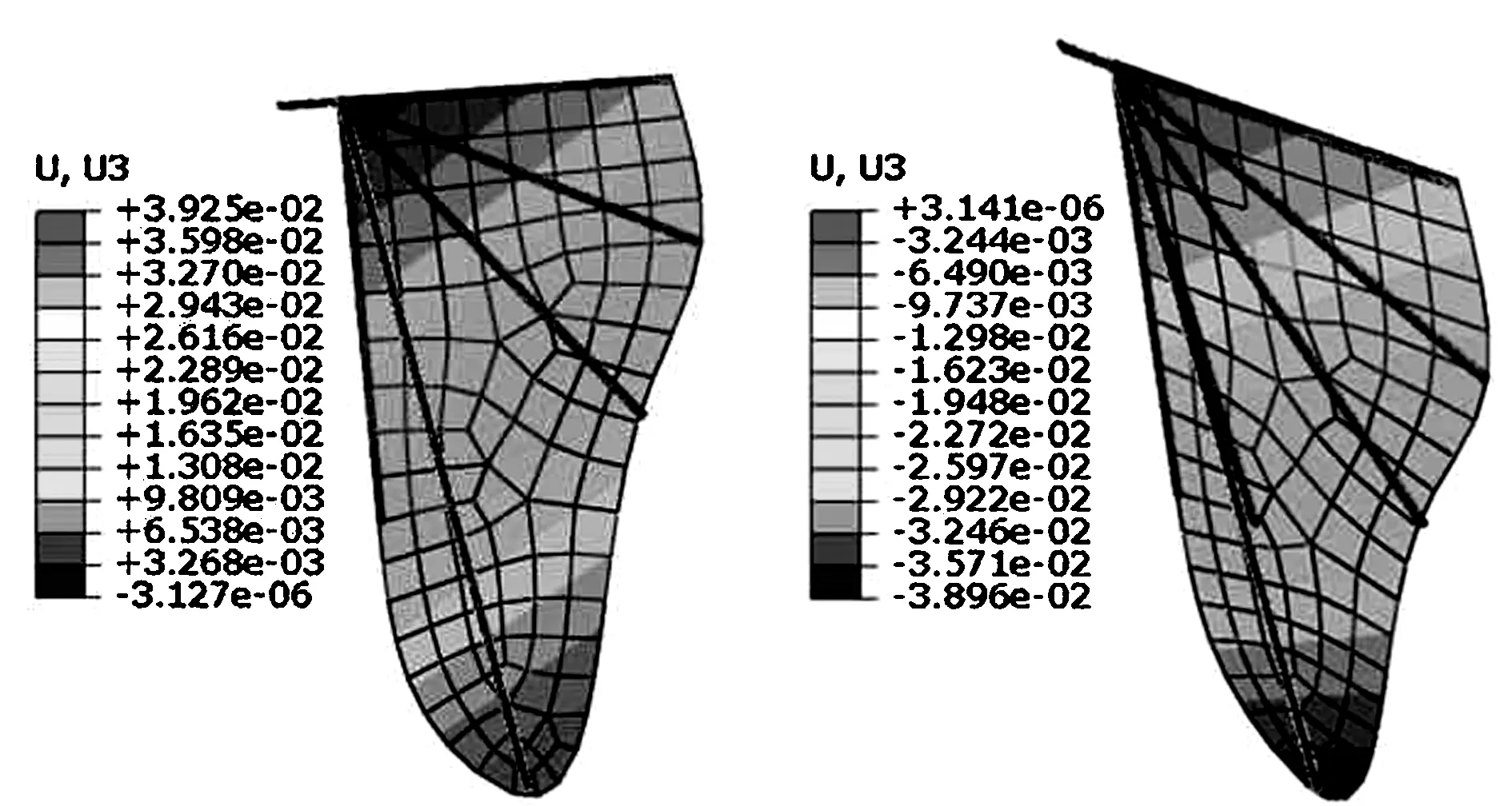
图7　上下拍动翅翼变形的有限元仿真Fig.7　Simulation of flapping wings

表1为所设计的翅翼的几何特性参数。表中，S为面积，L为展长，W为弦长，λ为展弦比。

表1　翅翼几何特性

2　气动力及力矩

本文的蜻蜓扑翼在空间的运动主要包括随质心的移动和绕质心的转动,可以简单地当作刚体进行研究。为了描述蜻蜓的飞行速度和运动轨迹,引入惯性坐标系;为了描述蜻蜓自身的姿态运动,引入体坐标系。

根据流体力学原理,取翼展上一个微面,将其视为二维刚性扑翼,其产生的瞬时气动力[9-10]为:

(9)

式中:dFN为翼面上垂直于翅膀平面的空气动力分量;dFC为平行于翅膀平面弦向的空气动力分量;dFS为平行于翅膀平面展向的空气动力分量;CN,CC,CS分别为翅膀法向、弦向和展向的空气动力系数;ρ为空气密度;c(r)为距昆虫质心距离为r的弦向长度;U为翅翼拍打速度。dFS对扑翼过程中产生的升力和阻力的影响特别小,可以忽略展向的空气动力在飞行器悬停中的影响。

法向和弦向的空气动力系数与迎角α有关,根据文献[3，11]可得到如下经验公式:

(10)

(11)

结合式(9)并沿翼展方向进行积分可得:

(12)

将法向气动力FN和弦向气动力FC在体坐标系内分解为升力和阻力:

(13)

以仿蜻蜓扑翼飞行器进行分析,上式所研究的为前翼的左翼产生的升力和阻力,因为左右翼是完全对称的,所以左右翼的升力和阻力完全相同。对于后翼,其升力和阻力为:

(14)

蜻蜓翅膀在受力的同时也受到力矩的作用,微面的气动力矩[12-13]为:

dML=FLrdr, dMD=FDrdr

(15)

对上式沿翼展方向进行积分,得到前后翼的气动力矩分别为:

(16)

由上式可知,气动力矩和气动力是关于翅翼拍动角速度的函数,而拍动角速度又可以表示为曲柄转角的函数,所以翅翼的气动力和气动力矩可以表示为曲柄转角的函数。

在1个周期内,扑翼产生的力和力矩为变量,采用1个周期内的平均力和力矩来表示:

(27)

式中:Fave,Mave分别为1个周期内的平均力和力矩;T为周期;F,M分别为瞬时力和力矩。

3　气动力分析

3.1单翼拍动气动力

以前翼拍动为例,图8给出了3个周期内的升力系数和阻力系数随时间的变化曲线,起始点为上挥极限位置,下一步将要进行下拍运动。

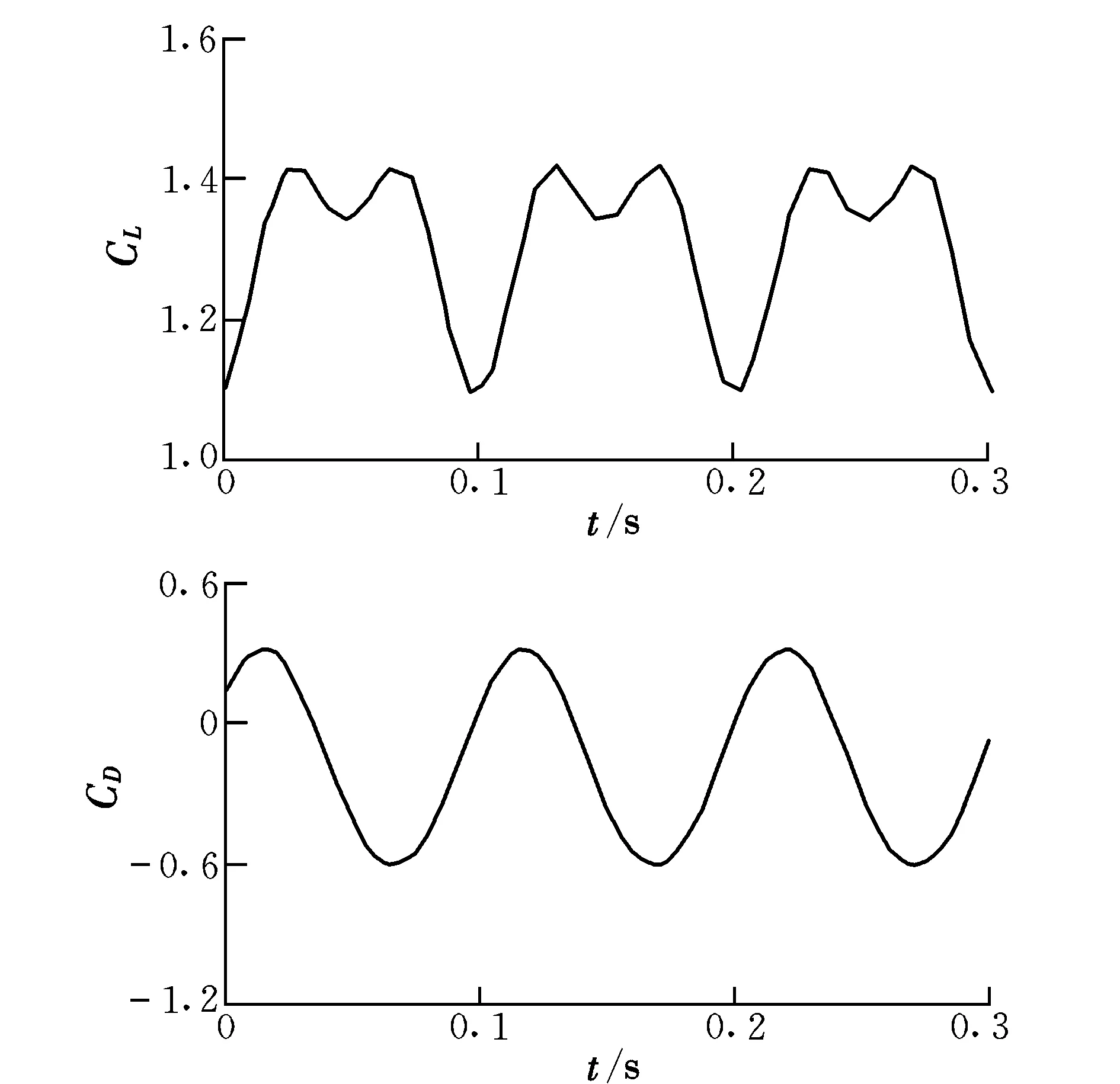
图8　单翼的升力系数和阻力系数变化曲线Fig.8　Lift and drag coefficients of a pair of flapping wings

整个周期内,升力系数有2个峰值,在上挥和下拍过程中各1个,这与文献[14]中的研究结果一致。下拍过程中,升力逐渐增大,当翼型面积与相对运动气流作用面积最大时,升力达到最大,然后逐渐减小,升力在上挥和下拍过程中都为正值,升力系数在1个周期内的平均值为1.304。

上挥运动时阻力为负,下拍运动时阻力为正,对于悬停过程中的蜻蜓来说,上挥和下拍运动中阻力系数往往是反对称的,即阻力在1个周期内相互抵消掉。但是在图8中可以看到,上挥时产生的阻力较大,1个周期内的阻力系数平均值为-0.143,这是因为翅翼挥拍过程中气动阻力造成曲柄不能匀速转动,间接影响了摇杆的运动规律所致。

3.2双翼拍动气动力

对于鸟类这种单扑翼飞行机理来讲,昆虫的双扑翼飞行机理具有更好的飞行性能。双翼挥拍过程中不同相位差是影响气动性能的重要参数,因此,双翼不同相位差下的性能好坏对于双扑翼飞行器的设计具有重大意义。前后翼相位差最大180°,分析中将双翼相位差分别从0°～180°每间隔90°取1个点,即同相、后翼领先1/4周期、反相,这分别代表了双翅翼拍打的3种主要特点。

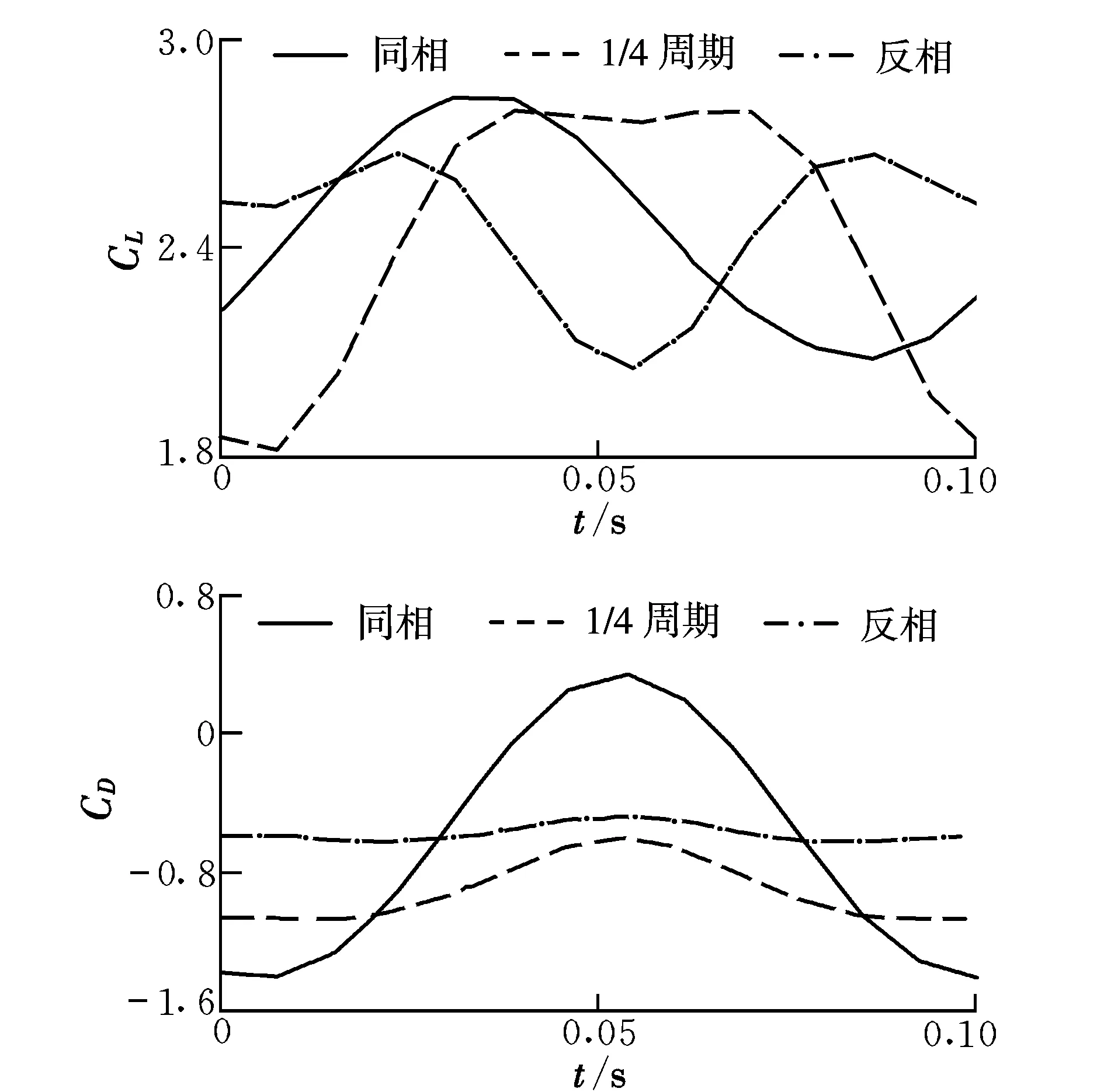
图9　不同拍动模式下升力系数和阻力系数变化曲线Fig.9　Lift and drag coefficients in different flapping mode

双翼同相拍动时和单翼鸟类飞行机理相似,此时升阻力的产生机理较为简单,昆虫起飞时大多采用同相拍动模式;后翼领先1/4周期时,前后翼上下拍动不同步,且拍动的同时有交汇,对于双翼拍动模式下的研究具有代表性。而反相拍动时,由于前后翼拍动周期一致,因此前后翼上下拍动的曲线完全相反,此时与蜻蜓悬停时两对翅膀相互协调拍打来调节升阻力的情况非常相似。图9为双翼挥拍过程中不同相位差[15-16](同相、后翼领先1/4周期、反相)时升力系数和阻力系数的变化曲线。

当前后翅翼同相拍动时,升力系数最大。后翼领先1/4周期情况下,升力幅值略小于同相拍动,大约有1/3周期内升力系数保持稳定,出现在前后翼交会的时刻。反相拍动时,升力变化速率较平缓,升力也比较小。在1个周期内，同相、后翼领先1/4周期、反相的平均升力系数分别为2.436,2.389,2.315。

后翼领先1/4周期拍动时,阻力系数最大,此时推力较大。而反相拍动时,阻力系数几乎保持恒定,此时阻力系数最小。当翅翼同相拍动时,阻力系数波动较大,但平均阻力系数小于后翼领先1/4周期。在1个周期内，同相、后翼领先1/4周期、反相的平均阻力系数分别为-0.745,-0.944,-0.594。

由以上分析可以看出:双翼同相拍动时升力具有最大值,这种拍动模式适合于起飞;后翼领先前翼1/4周期拍动时,升力小于双翼同相拍动,但推力最大,这种拍动模式适合于加速前飞。前后翼反相拍动时,阻力和升力都最小,这种模式适合于最省力的巡航飞行。

4　结束语

本文针对仿蜻蜓扑翼飞行机理与鸟类单翼飞行机理的不同,基于非定常空气动力学原理建立了仿蜻蜓扑翼飞行器的动力学模型,分析了气动力和力矩,并对双翼挥拍过程中不同相位差所受到的气动力进行了计算,分析结果对双翅翼微型飞行器机构设计与研究有一定的理论指导意义。

[1]Wang J Z.The role of drag in insect hovering[J].Journal of Experimental Biology,2004,207(23):4147-4155.

[2]Dudley R.The biomechanics of insect flight[J].Journal of Biomechanics,2003,36(2):307-308.

[3]Sun M,Tang J.Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J].Journal of Experimental Biology,2002,205(1):55-70.

[4]Deng X,Schenato L,Sastry S.Model identification and attitude control scheme for a microme chanical-flying insect[C]//Proceedings of the 7th ICARCV.Singapore:IEEE,2002:1007-1012.

[5]魏榛,高东奇,贾立超,等.一种用于研究鹰蛾悬停飞行的扑翼实验装置[J].实验力学,2010,25(4):393-400.

[6]Mazaheri K,Ebrahimi A.Experimental investigation of the effect of chord wise flexibility on the aerodynamics of flapping wings in hovering flight[J].Journal of Fluids and Structures,2010,26(4):544-558.

[7]Hollenbecka A C,Palazottob A N.Methods used to evaluate the hawkmoth as a flapping-wing micro air vehicle[J].International Journal of Micro Air Vehicles,2012,4(2):119-132.

[8]杨智春,李思政,舒忠平,等.一种柔性微型扑翼设计及其气动力特性的试验研究[J].机械科学,2006,25(1):12-14.

[9]Sane S P.The aerodynamics of insect flight [J].Journal of Experimental Biology,2003,206(23):4191-4208.

[10]夏风,张剑波,张蓬蓬.一种微型仿昆扑翼飞行器扑翼操控机制[J].飞行力学,2010,28(1):16-19.

[11]Isogai K,Fjishirou S.Unsteady three-dimensional viscous flow simulation of a dragonfly hovering [J].AIAA Journal,2004,42(10):2053-2059.

[12]Lai W,Yan J,Motamed M,et al.Force measurements on a scaled mechanical model of dragonfly in forward flight[C]//International Conference on Advanced Robotics.Icar,2005:595-600.

[13]Yamamoto M.Direct measurement of unsteady fluid dynamic forces for a hovering dragonfly[J].AIAA Journal,2012,43(43):2475-2480.

[14]Liu H,Ellington C,Kalachi K.A computational fluid dynamic study of hawkmoth hovering [J].Journal of Experimental Biology,1998,201(3):461-477.

[15]Maybury W J,Lehmann F O.The fluid dynamics of flight control by kinematics phase lag variation between two robotic insect wings [J].Journal of Experimental Biology,2004,207(26):4707-4726.

[16]Alexander D E.Unusual phase relationships between the forewings and hindwings in flying dragonflies[J].Journal of Experimental Biology,1984,109(1):379-383.

(编辑：崔立峰)

Mechanism design and aerodynamic research on a dragonfly flapping-wing air vehicle

SUN Wei, FENG Chun-peng

(College of Mechanical and Electrical Engineering, North China University of Technology,Beijing 100144, China)

In consideration of the distinction between dragonfly flapping wing flight and the bird’s single wing flight mechanism, we designed the double-wing spatial four-bar flapping wing mechanisms and introduced asymmetric stiffness flexible flat wings in this paper. In comparison with downstroke, the stiffness of wings was smaller and the deformation of wings was more obvious in upstroke. As a consequence, the air resistance generated during upstroke was decreased, and then the equivalent lift of each flapping cycle was enhanced. Finally, the energy consumption speed was reduced and flight efficiency was increased when the air vehicle. Based on the unsteady aerodynamics force model, the dynamic model of dragonfly flapping-wing air vehicle is established and the contrastive analysis of lift and drag coefficient change between the different phase difference during the double-wing swinging(In-phase, a difference of 1/4 period,anti-phase) is performed in this study, which can provide a theoretical basis for selection of different flapping model.

double wings; asymmetric stiffness; different phase

2015-12-10;

2016-03-21; 网络出版时间:2016-03-23 14:10

孙卫(1990-)，男，山东济宁人，硕士研究生，研究方向为扑翼飞行器设计。

V214.19; V211.59

A

1002-0853(2016)05-0021-05