联合低轨卫星和地面监测站数据确定导航卫星轨道

冯来平　阮仁桂　吴显兵　孙碧娇

1　信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2　西安测绘研究所，西安市雁塔路中段1号，710054 3　地理信息工程国家重点实验室，西安市雁塔路中段1号，710054



联合低轨卫星和地面监测站数据确定导航卫星轨道

冯来平1,2,3阮仁桂2,3吴显兵2,3孙碧娇2,3

1信息工程大学地理空间信息学院，郑州市科学大道62号，450001 2西安测绘研究所，西安市雁塔路中段1号，710054 3地理信息工程国家重点实验室，西安市雁塔路中段1号，710054

探讨同时利用星载数据和地面监测站数据进行导航卫星联合定轨的方法。为验证该方法的有效性，利用2011-03-16～31中国境内7个GPS监测站的观测数据和GRACE-A&B星载数据进行定轨实验。结果表明，在7个国内监测站基础上，加入一颗低轨卫星(GRACE-B)星载GPS数据,GPS可见弧段增加约14%，卫星径向、切向和法向(R、T、N)定轨精度可分别提高约35%、44%和45%；若同时加入GRACE-A和GRACE-B星载数据，可见弧段增加约18%，R、T、N分量精度分别提高约51%、60%和62%。该方法为区域监测站布设条件下导航卫星定轨精度的提升提供了一种新思路。

低轨卫星；星载数据；精密定轨；SPODS软件; 区域站

导航卫星的轨道和钟差通过地面监测站观测数据解算得到，其精度决定了用户定位授时的精度。数量多、分布广的地面监测站可获得对卫星的更多观测，对于提高卫星轨道和钟差精度至关重要。而一些新兴的导航卫星系统，其地面监测站规模尚小，又不具备建设海外监测站的条件，难以实现对导航卫星的全弧段连续跟踪，难以实现高精度定轨，如采用国内监测站伪距数据进行GPS定轨，精度约为10 m；采用载波相位定轨，精度约为1 m。研究表明，即使采用载波相位定轨，由于星座几何构型的影响，北斗MEO卫星定轨精度低于GPS卫星2、3倍，GEO精度更差[1-2]。近年来，以GPS、北斗为代表的导航卫星系统寄希望于通过建立导航卫星之间的测量链路实现全弧段跟踪，从而实现高精度定轨[3-6]。事实上，凭借独有的连续三维定位能力，导航卫星系统已经成为低轨卫星的主要测轨手段。当前，基于星载GPS的低轨卫星定轨精度已达1～2 cm[6-8]，众多对位置精度要求较高的低轨卫星上也已搭载了星载GPS接收机，如TOPEX、CHAMP、Jason、GRACE、GOCE等。这些星载接收机可获得高精度的伪距和载波观测数据，如果将这些低轨卫星视为运动的监测站，便可将星载数据与地面监测站数据共同用于确定导航卫星的精密轨道。对于地面观测站，低仰角卫星观测量易受多路径等因素的影响，为保证观测数据的质量，通常需要设置0°～15°测站高度角；而低轨卫星周围不存在遮挡，且其轨道高于对流层，对于低高度角、甚至负高度角的GNSS卫星观测量，其所受的影响比地面站小；再者，作为“运动监测站”的低轨卫星在空间观测几何上对GNSS具有增强作用[9]，使低轨卫星和GNSS卫星定轨精度都得到改善。Zhu[10]提出将低轨卫星(GRACE和CHAMP)星载GPS数据和地面监测站数据“一体化”处理，同时确定低轨卫星和GPS卫星轨道、地心坐标和地球引力场系数的方法，可明显提高两类卫星的轨道精度和地球动力学参数精度。耿江辉[11]利用星载数据和地面监测站数据进行GPS卫星定轨实验，亦得出类似的结论。这些研究成果清晰地表明，利用星载数据可以增强导航卫星轨道确定的精度。以上研究都是基于全球布站的情况展开讨论和实验分析的，本文以中国在建的北斗全球导航卫星系统为研究背景，探讨在区域监测站布设情况下，利用低轨卫星星载数据增强导航卫星定轨的可行性。讨论了联合定轨方法和力学模型，并分析了在中国区域7个GPS监测站基础上加入GRACE卫星星载数据后对GPS卫星跟踪弧段和定轨精度的改进情况。

1　数学模型

地面监测站数据和星载数据联合处理观测模型可以简单表示如下：

(1)

其中，Lsta、Lleo分别表示地面监测站接收机和星载接收机获得的GPS观测数据，vsta、vleo分别为相应的测量误差，Psta、Pleo为对应的权矩阵；t为时间参数；xgps、xleo分别为GPS轨道参数和低轨卫星轨道参数；xsta为测站有关的参数，如站坐标、对流层延迟参数等；xo为观测量相关的参数，如载波相位模糊度、钟差参数等。

对上述观测方程进行线性化并写成如下矩阵形式：

(2)

其中，

式中，(·)0表示参数初值，δ(·)表示参数的改正数，则对应的最小二乘解可以表示为：

(3)

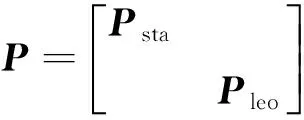
在定轨任务中，测站坐标通常精确已知，可以作为已知量。而低轨卫星围绕地球高速运动，轨道是未知的，且其受力复杂，尤其是太阳光压和大气阻力难以模型化。因此，相比传统的导航卫星精密定轨，利用星载数据进行导航卫星轨道确定的关键是如何高精度地描述低轨卫星轨道。

2　定轨方法

星载GPS的应用不仅大幅度提高了低轨卫星的轨道确定精度，也推动了低轨卫星定轨技术的发展。目前，低轨卫星主要的定轨方法有动力学法、运动学法和约化动力学法。过去20多年中，在国外重力卫星和测高卫星(如CHAMP、GRACE、GOCE、TOPEX、Jason-1/2等)的轨道确定中，为了避免轨道动力学模型误差(尤其是地球引力场模型误差)的影响，主要采用约化动力学法和几何法进行卫星轨道的确定[7-8,12-18]，这些卫星的重要科学成果之一，就是极大地改进了地球引力场模型的精度，使得低轨卫星的动力学模型精度大幅度提高。目前，利用最新的地球引力场模型进行低轨卫星动力学定轨，精度可以达到5cm以内[7]。动力学法是直接恢复卫星相关参数(如轨道参数、地球重力场参数、地球质心位置等)的有效方法。此外，动力学法可以利用任何等间隔或非等间隔采样的数据，同时获得卫星的位置和速度。本文的目的是利用低轨卫星星载GPS数据增强GPS卫星的精密定轨，应该避免采用运动学法和约化动力学法，因为二者的未知参数数量较多；另外，通过当前先进的轨道动力学模型约束低轨卫星轨道，可以使得低轨卫星轨道获得更多的信息，而这些信息也会增强GPS卫星的结构[9]。因此，本文采用动力学定轨方法描述低轨卫星轨道。

为保证轨道动力学模型的准确性，考虑的力模型应包括地球引力场、日、月及行星引力、太阳光压摄动力、后牛顿效应等。GPS卫星和低轨卫星的力模型分别如表1所示。

表1　GPS卫星和低轨卫星力模型

值得说明的是，表1中太阳光压和大气阻力模型具有很大的不确定性，它们的模型系数要与轨道初始状态参数一起作为未知参数求解。对于GPS卫星，求解5个参数(D0、Y0、B0、Bc和Bs)可以获得理想的轨道解[20]。对于低轨卫星，太阳光压反射系数和大气阻力系数每6 h估计一个常数。此外，每个轨道周期估计一组径向、迹向和法向的周期性经验力参数[21]。

我们在SPODS (satellite positioning and orbit determination system)软件基础上进行了功能扩展[22]，增加了联合利用星载GNSS数据和地面监测站数据进行导航卫星定轨的功能，以下实验基于该软件完成。

3　实验及分析

3.1实验数据

为评估联合低轨卫星星载数据和区域监测站数据进行GPS卫星定轨的效能，收集GRACE-A和GRACE-B两颗卫星的星载数据，联合中国境内7个GPS跟踪站(BJFS、KUNM、LAHZ、SHAO、URUM、CHAN和XIAN)的观测数据进行分析和实验。GRACE是美国NASA和德国DLR共同提出的以地球引力场反演和探测大气、电离层环境实验为目的的卫星项目，GRACE采用低低卫星跟踪技术，由两颗在同一轨道相距220±50 km、前后运行的卫星构成，轨道倾角89°，高度485～500 km，约90 min绕地球一圈[23]。两颗卫星均搭载有星载GPS接收机，用于精确确定其位置。观测时段为2011-03-16～31。

为了便于比较和说明问题，计算分析中设置了以下3个实验方案：方案1，采用国内7个GPS跟踪站观测数据；方案2，采用国内7个GPS跟踪站观测数据和GRACE-B卫星星载GPS观测数据；方案3，采用国内7个GPS跟踪站观测数据和GRACE-A、GRACE-B卫星星载GPS观测数。

针对以上3种方案分别进行定轨处理，定轨数据采用3 d弧段，数据采样间隔为30 s。实验假设星载数据和地面监测站数据测量精度相当，依据我们的经验，消电离层组合伪距和相位的精度分别设为2 m和2 cm，依此进行赋权。如前所述，为降低多路径影响，地面站截止高度角取10°；低轨卫星周围不存在遮挡物，截止高度角取5°。待估参数除卫星轨道参数外，还包括非差消电离层组合模糊度参数以及测站对流层天顶延迟，其中模糊度参数采用浮点解。GPS卫星的初始轨道参数通过广播星历计算得到；对于GRACE卫星，首先利用广播星历和伪距观测数据进行运动学定轨，然后通过动力学平滑获得轨道初始状态矢量和动力学模型参数初值。为了分析低轨卫星星载数据的作用，首先分析不同方案GPS定轨几何结构的变化，然后以IGS精密轨道作为参考轨道分析不同方案的定轨外符合精度。

3.2定轨几何结构分析

低轨卫星的加入必然带来定轨几何结构的增强。首先表现在可见弧段的增加，在此定义可见弧段为至少被一个监测站观测到的时段。图1统计了算例中不同方案中GPS各颗卫星的可见弧段。可以看出，方案1中，各卫星的可见弧段为30.2%～41.8%，平均约为36.8%。方案2中，除30号卫星外，各GPS卫星的可见弧段比例略有提高，为35.2%～57.3%，平均约为50.8%，比方案1增加了约14.0%，相对提高约38.0%。由于GRACE-B卫星没有观测到30号卫星，所以该星的可见弧段没有变化。方案3中，各颗卫星的有效弧段都得到显著增加，为47.3%～60.5%，平均约为54.6%，比方案1增加17.8%，相对提高约48.4%，比方案2增加了3.8%。

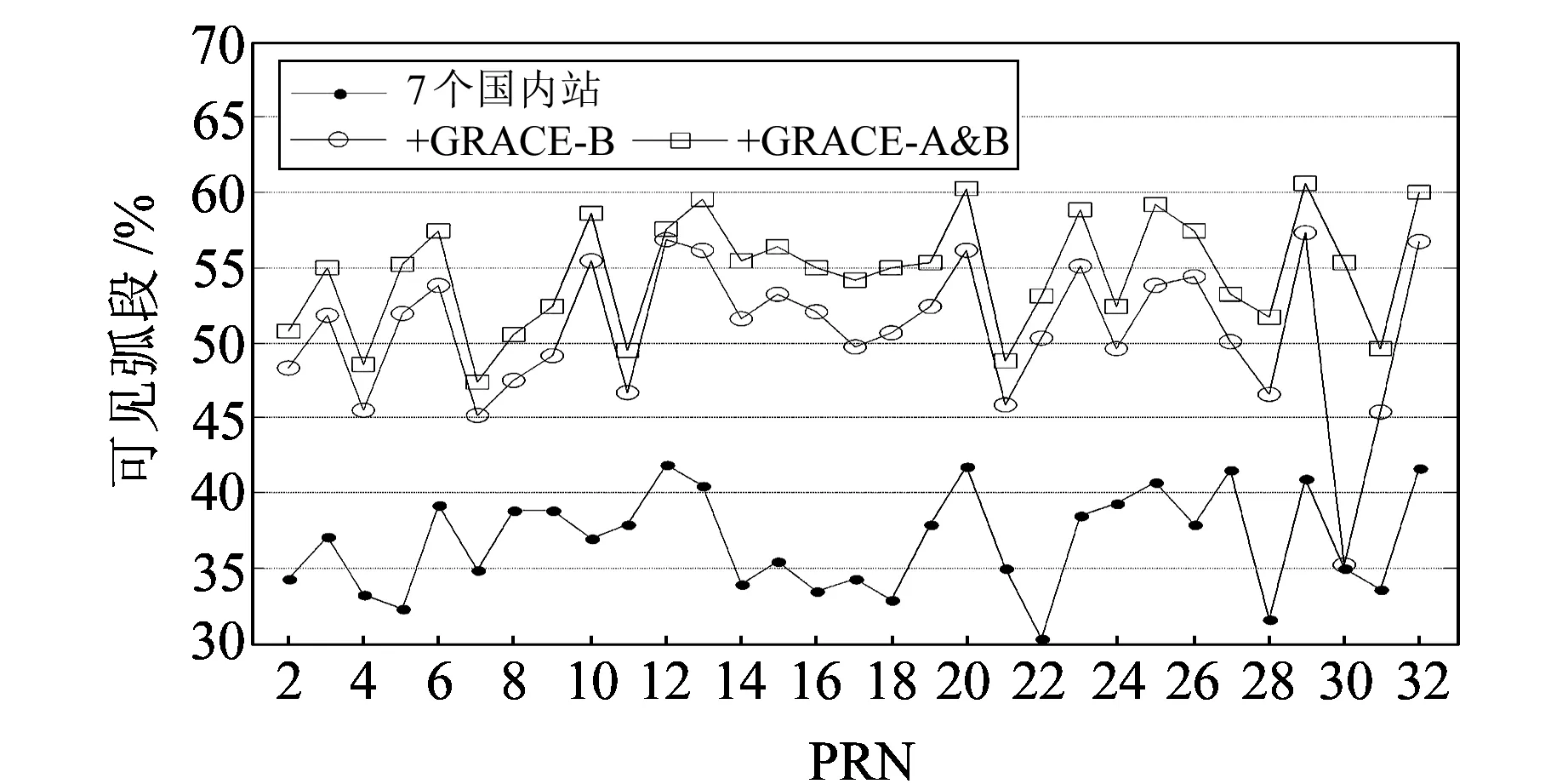
图1　3种方案GPS卫星可视弧段比较Fig.1　Comparison among the visibility of GPS satellites from three solutions

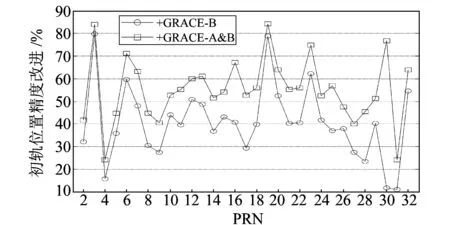
图2　方案2和方案3相对于方案1各卫星初始三维位置精度的改进Fig.2　Improvement of the satellites initial position precision by solution 2 & 3 compared with solution 1

3.3定轨精度分析

图3给出了3种方案定轨结果与IGS最终轨道在R、T、N方向以d为单位统计的RMS。可以看出，方案1中，轨道径向(R)方向的RMS为0.2 m左右，切向(T)和法向(N)均约0.6 m；方案2中，R、T、N方向的RMS均得到显著降低，R方向的RMS约为0.1 m，T和N方向的RMS基本小于0.4 m。表2(单位m)统计了16 d的平均轨道R、T、N方向和3维位置的RMS。方案1、方案2和方案3的轨道三维位置精度分别为0.952 m、0.521 m和0.361 m，其中方案3的轨道径向精度可达0.1 m。相比于方案1，方案2和方案3的改进幅度分别为约45%和62%。

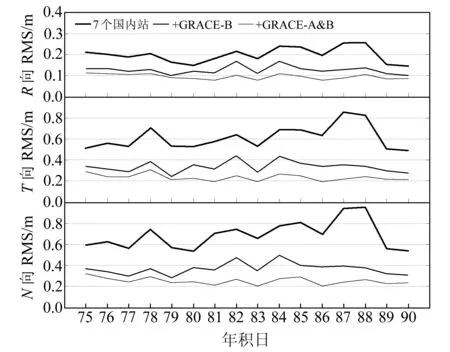
图3　3种方案定轨结果与IGS轨道在R、T、N方向的RMSFig.3　Daily RMS in RTN of different solutions compared with IGS final orbits

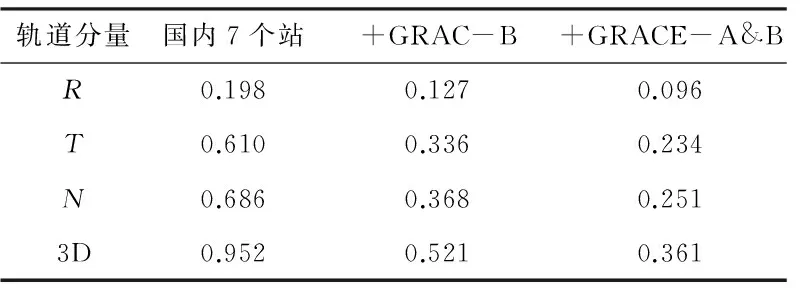
轨道分量国内7个站+GRAC-B+GRACE-A&BR0.1980.1270.096T0.6100.3360.234N0.6860.3680.2513D0.9520.5210.361

图4给出了方案2、3相对于方案1轨道精度的改进情况。可以看出，方案2中R方向RMS的改进幅度在17%～49%之间，T方向在32%～58%之间，N方向在30%～60%之间，R、T、N方向的平均改进幅度分别约为35%、44%和45%。方案3的轨道精度进一步提高，R方向的改进幅度为42%～65%，T方向为43%～75%，N方向为46%～73%，R、T、N方向的平均改进幅度分别约为51%、60%和62%。这说明，星载数据带来轨道T方向和N方向的改进更加明显，虽GRACE双星相距仅200多km，但却带来了轨道精度的显著改善。

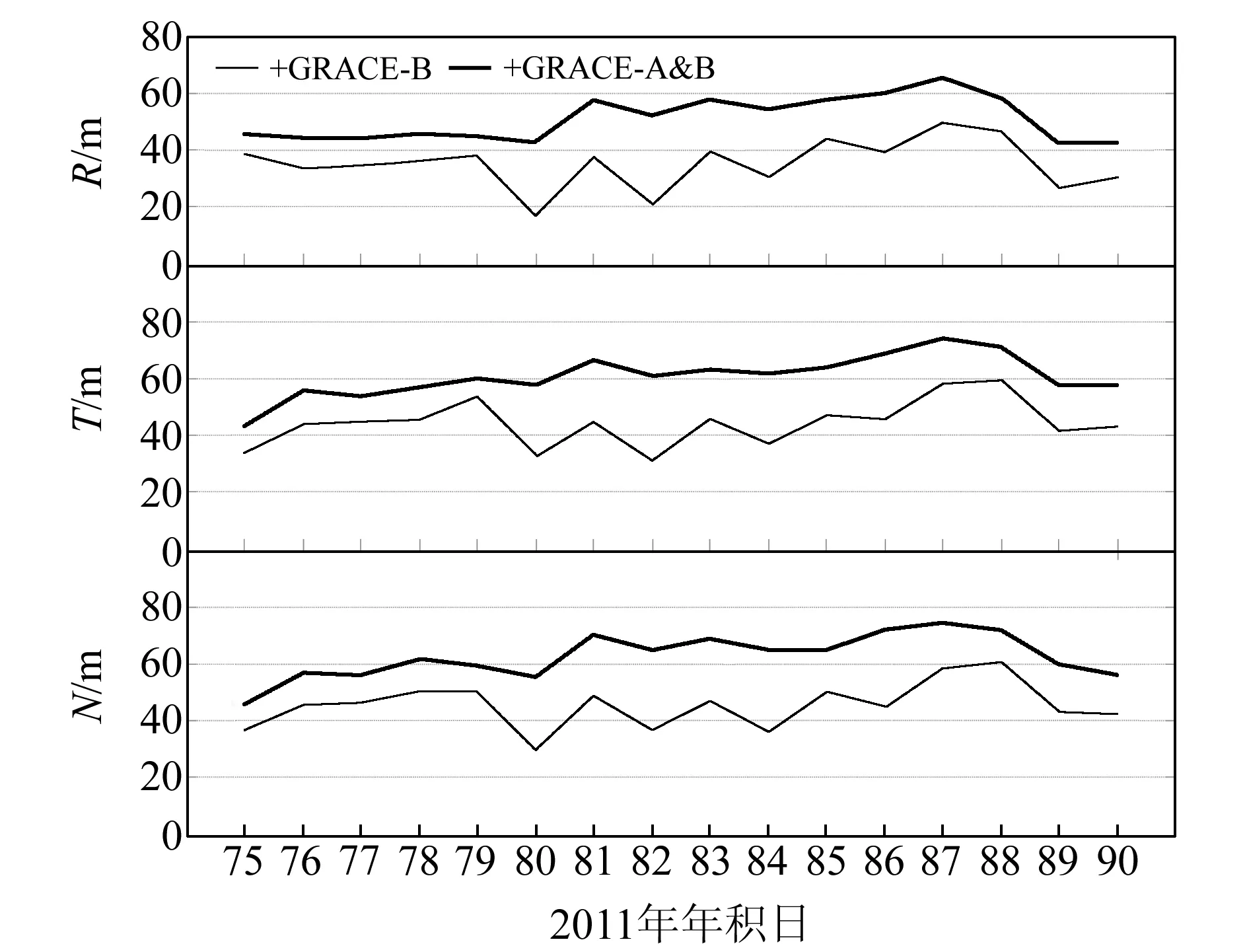
图4　方案3和方案2相对于方案1的轨道精度改进程度Fig.4　Improvements of orbit accuracy by solution 2 & 3 compared with solution 1

图5是按卫星号统计的轨道精度改进情况。加入一颗LEO卫星后，除30号卫星外，轨道R方向的改进幅度约为11%～63%，T方向的改进幅度约为25%～64%，N方向的改进幅度约为25%～65%。值得注意的是，PRN 30号卫星虽然没有直接被GRACE-B卫星观测到，但是由于在定轨解算过程中各卫星轨道之间的相关性，其轨道R、T、N方向也得到不同程度的改进，分别提高了7%、9%和13%。当同时加入GRACE-A&B卫星时，各GPS卫星轨道R方向的改进幅度为15%～76%，T方向改进幅度为31%～78%，N方向改进幅度为37%～80%。

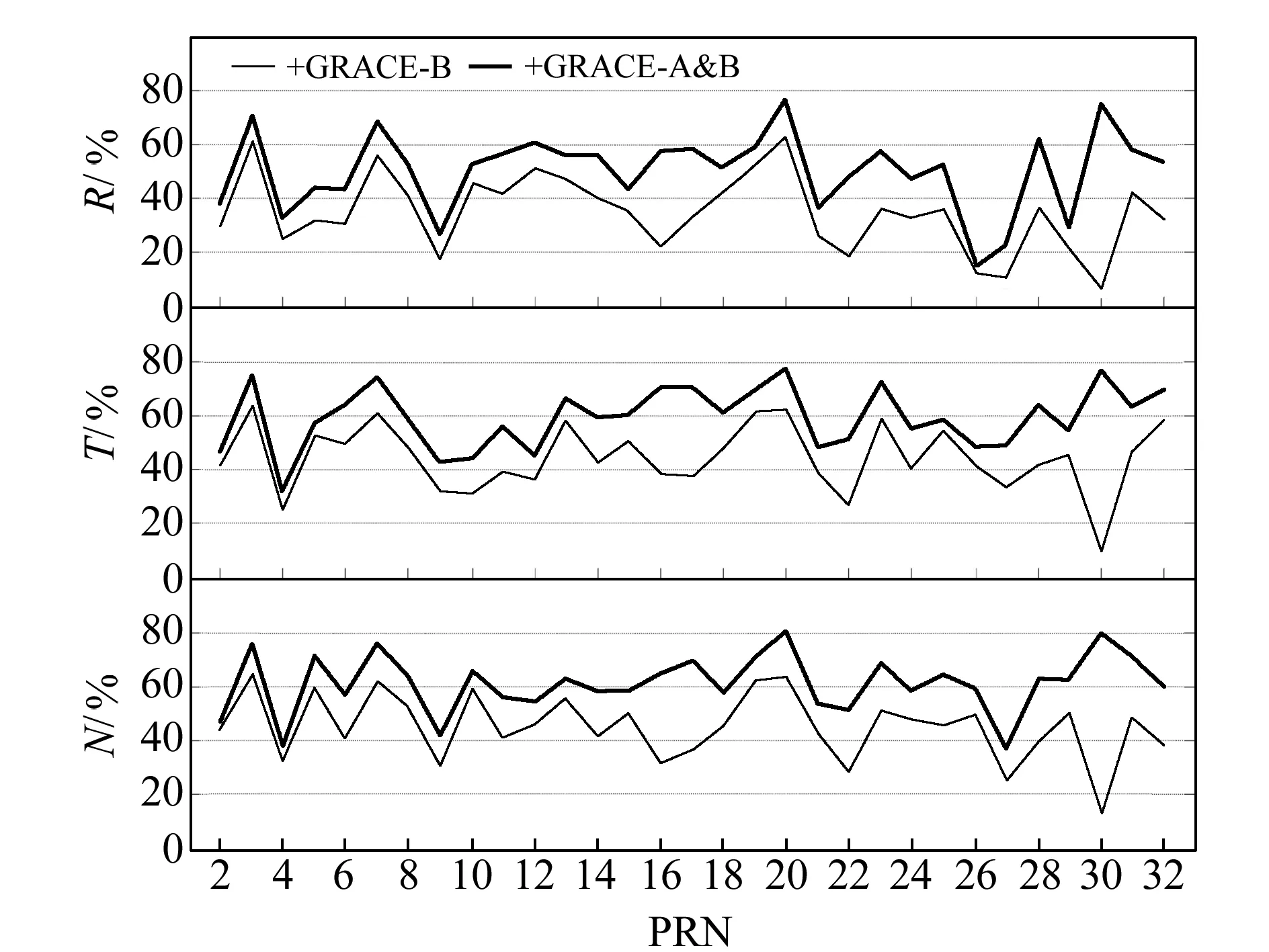
图5　按卫星统计的轨道精度改进Fig.5　Improvements of orbit accuracy respective to satellites

4　结　语

通过加入低轨卫星星载数据，实现联合星载数据和地面监测站数据的导航卫星定轨，可有效提高区域监测站条件下导航卫星精密定轨的精度。本文分析表明，通过加入低轨卫星星载GPS数据，可有效提高导航卫星的可见弧段，增强定轨的几何结构。定轨实验表明，在7个国内监测站基础上，加入GRACE-B卫星星载GPS数据,使得GPS卫星可见弧段增加约14%，R、T、N方向的定轨精度分别提高约35%、44%和45%；当同时加入GRACE-A、GRACE-B卫星数据时，可见弧段增加约18%，R、T、N分量的精度分别提高约51%、60%和62%。这也说明，类似于GRACE这样的卫星编队，相比于单颗的低轨卫星，其在这两个方面的贡献更加显著。可以设想，借助于一定数量、轨道分布合理的低轨卫星，并结合国内区域跟踪站，完全有可能实现对导航卫星的有效跟踪和高精度定轨。

[1]周善石，胡小工，吴斌，等. 区域监测网精密定轨与轨道预报精度分析[J]. 中国科学:物理学力学天文学，2010,40(6): 800-808(Zhou Shanshi, Hu Xiaogong,Hu Bin, et al, Analysis of Orbit Determinnation and Prediction Accuracy for a Regional Tracking Network[J]. Scientia Sinica:Phys, Mech & Astron, 2010,40(6): 800-808)

[2]宋小勇. COMPASS导航卫星定轨研究[D].西安：长安大学，2009(Song Xiaoyong. Study on the Orbit Determination of COMPASS Navigation Satellites[D]. Xi’an:Chang’an University,2009)

[3]Amarillo F F. Inter Satellite Ranging and Inter-Satellite Communication Links for Enhancing GNSS Satellite Broadcast Navigation Data[J]. Advances in Space Research, 2011,47(5):786-801

[4]Ananda M P, Bernstein H. Global Positioning System Autonomous Navigation[C]. IEEE Position, Location and Navigation Symposium ,Las Vegas, Nevada, 1990

[5]林益明，何善宝，郑晋军,等. 全球导航星座星间链路技术发展建议[J]. 航天器工程,2010,19(6): 1-7(Lin Yiming, He Shanbao, Zheng Jinjun, et al. Development Recommendation of Inter-Satellites Links in GNSS[J].Spacecraft Engineering. 2010,19(6): 1-7)

[6]秦显平. 星载GPS 低轨卫星定轨理论及方法研究[D]. 郑州: 信息工程大学, 2009(Qin Xianping. Space-Borne GPS Low Earth Orbit Research Theory and Method of Satellite Orbit[D]. Zhengzhou: Information Engineering University,2009)

[7]徐天河, 江南, 孙张振. 基于GOCE卫星几何轨道的动力学平滑研究[J]. 测绘科学与工程, 2013,33(1): 16-20(Xu Tianhe, Jiang Nan, Sun Zhangzhen. Studies Dynamics Smoothing for GOCE Satellite Kinematic Orbit[J]. Geomatics Science and Engineering, 2013,33(1): 16-20)

[8]Svehla D, Rothacher M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003(1): 47-56

[9]Rothacher M. Precise Orbit Determination for Low Earth Orbiters[R].Colloquium on Atmospheric Remote Sensing Using the Global Positioning System,2004.

[10]Zhu S, Reigber C, Konig R. Integrated Adjustment of CHAMP, GRACE, and GPS Data[J]. Journal of Geodesy, 2004,(78): 103-108

[11]耿江辉, 施闯, 赵齐乐,等. 联合地面和星载数据精密确定GPS卫星轨道[J]. 武汉大学学报:信息科学版, 2007,32(10): 906-909(Geng Jianghui, Shi Chuang, Zhao Qile, et al. GPS Precision Orbit Determination from Combined Ground and Space-Borne Data[J]. Geomatics and Information Science of Wuhan University, 2007,32(10): 906-909)

[12]赵齐乐．GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]．武汉：武汉大学，2003(Zhao Qile. Research on Precision Orbit Determination Theory and Software of both GPS Naviagation Constellation and LEO Satellites[D].Wuhan: Wuhan University ,2003)

[13]Bock H, Jaggi A, Svehla D, et al. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007,39(10): 1 638-1 647

[14]Schutz B E, Tapley B D, Abusali P A M, et al. Dynamic Orbit Determination Using GPS Measurements from TOPEX/POSEIDON[J]. Geophysical Research Letters, 1994,21(19): 2 179-2 182

[15]Svehla D, Rothacher M. Kinematic Positioning of LEO and GPS Satellites and IGS Stations on the Ground[J]. Advances in Space Research, 2005,36(3): 376-381

[16]Wu S C,Yunck T P, Thornton C L. Reduced-Dynamic Technique for Precise Orbit Determination of Low Earth Satellites[J]. Journal of Guidance, 1990,14(1): 24-24

[17]Yunck T P, Bertiger W I, Wu S C, et al. First Assessment of GPS-Based Reduced Dynamic Orbit Determination on TOPEX/Poseidon[J]. Geophysical Research Letters, 1994,21(7): 541-544

[18]李建成, 张守建, 邹贤才，等. GRACE 卫星非差运动学厘米级定轨[J]. 科学通报, 2009,54(16): 2 355-2 362(Li Jiancheng, Zhang Shoujian, Zou Xiancai, et al. Precise Orbit Determination for GRACE with Zero-Difference Kinematic Method[J]. Chinese Sci Bull, 2009,54(16): 2 355-2 362)

[19]McCarthy D D, Petit G. IERS Conventions (2003)[R].Verlag des Bundesamtes fur Kartographie und Geodasie, Frankfurt am Main 2004, 2004

[20]Springer T A. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D]. Berne, Switzerland: Astronomical Institute, University of Berne, 1999

[21]Bock H. Efficient Methods for Determining Precise Orbits for Low Earth Orbiters Using the Global Positioning System (GPS)[D]. Bern: University of Bern, 2003

[22]魏子卿, 阮仁桂, 贾小林, 等. 卫星定位定轨系统SPODS:理论与测试[J]. 测绘学报, 2014,43 (1):1-4 (Wei Ziqing, Ruan Rengui, Jia Xiaolin, et al. Satellite Positioning and Orbit Determination System SPODS: Theory and Test[J]. Acta Geodaetica et Cartographica Sinica, 2014,43(1): 1-4)

[23]陈俊平.低轨卫星精密定轨研究[D]. 上海：同济大学, 2007 (Chen Junping. Precise Orbit Determination of Low Earth Orbiters[D]. Shanghai: Tongji University, 2007)

About the first author:FENG Laiping, PhD candidate, senior engineer,majors in GNSS orbit determination and positioning technology,E-mail:fenglaiping@163.com.

Precise Orbit Determination of Navigation Satellite Using Joint Data from Regional Tracking Station and LEO

FENGLaiping1,2,3RUANRengui2,3WUXianbing2,3SUNBijiao2,3

1Institute of Surveying and Mapping, Information Engineering University, 62 Kexue Road,Zhengzhou 450001, China 2Xi’an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road,Xi’an 710054, China 3State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road,Xi’an 710054, China

We discuss the method of orbit determination combining the on-board data of LEO with the observation data of regional monitor stations. In order to validate this proposed approach and its performance, the observation data of 7 GPS stations in China and on-board data of GRACE-A&B during March 16-31, 2011 are collected and orbit determination experiments were carried out. The results show that, compared with the result of 7 stations, the visibility of GPS satellites is increased by about 14%. Meanwhile, the precision of GPS orbits expressed inR,T,Ncomponents are improved by about 35%, 44% and 45% respectively when introducing only GRACE-B; improvements inR,T,Ncomponents of 51%, 60% and 62% are achieved when both GRACE-A and GRACE-B are introduced and the visibility of GPS satellites is increased by 18% in this case. The proposed approach provides a new means to improve the orbit determination accuracy of navigation satellites under the restriction of regional monitoring stations.

LEO；on-board data； precise orbit determination；SPODS；regional stations

National Natural Science Foundation of China, No. 41104019; Open Fund of State Key Laboratory of Geodesy and Earth’s Dynamics, No. SKLGED2014-3-4-E.

2015-10-13

冯来平，博士生，高级工程师，主要从事GNSS精密定轨与定位技术研究，E-mail:fenglaiping@163.com。

10.14075/j.jgg.2016.10.005

1671-5942(2016)010-0864-06

P228

A

项目来源：国家自然科学基金(41204020)；大地测量与地球动力学国家重点实验室开放基金(SKLGED2014-3-4-E)。