重力数据误差对大地水准面模型建立的影响
2016-10-27李姗姗曲政豪
李姗姗 曲政豪
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
重力数据误差对大地水准面模型建立的影响
李姗姗1曲政豪1
1信息工程大学地理空间信息学院,郑州市科学大道62号,450001
基于Stokes理论建立的大地水准面模型,其精度受重力数据误差,即重力数据分辨率、精度以及积分范围的影响。针对这一问题,通过重力场谱特征分析,给出不同地形区域重力数据分辨率以及积分半径造成的大地水准面高频截断误差的量级大小,计算平均重力异常误差对大地水准面建模精度的影响。研究成果对不同地形区域cm级大地水准面模型的建立具有理论与指导意义。
截断误差;大地水准面;平均重力异常;代表误差;积分半径
建立高精度高分辨率的大地水准面模型需要有地面上的重力异常。因为测量总是在地面离散点上进行,不能满足理论上连续分布的数据要求,因此以重力异常计算大地水准面时,都是使用数值化的方法来实现。最为常见的是将积分的球面划分成若干个面积,以该面积内或其周围已知的重力异常推求出该面积的平均重力异常,再用求和的方法完成积分的数值计算。由上述或等价的其他数值方法确定大地水准面将产生来自两个方面的误差:一是模型误差,即解式本身的误差(如地形起伏影响、球近似的影响等),可通过提高解式的严密性来减弱[1-4];二是源于重力数据的误差,体现在平均重力异常的分辨率(即面积大小)、积分半径的选取及其精度两个方面。本文拟针对1′×1′ cm级大地水准面模型的建立,研究分析不同地形区域对积分半径选取以及平均重力异常精度的要求。
1 重力数据的分辨率与精度
利用Stokes-Pizzetti公式计算大地水准面可表示为[5-6 ]:
(1)
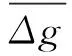
(2)
在实际应用中,显然不可能采用全球积分。对于局域大地水准面模型的建立,一般采用求和的方法完成积分的数值计算,即将(1)式表示成如下的形式:
(3)
从式(3)可以看出,大地水准面模型建立的精度主要受两部分影响:一方面,平均重力异常的格网面积越小,即数值积分的单元面积划分越细,积分范围越大,则数值积分的结果就越精确;另一方面,水准面的精度还受到网格平均重力异常误差的影响,这一误差主要因为观测值稀疏与数据处理不完善造成。可将大地水准面建模误差分为由平均重力异常分辨率以及积分半径引起的截断误差部分m1和平均重力异常误差所引起的误差部分m2,即
(4)
2 截断误差计算
取计算点周围(球冠半径为ψ0)1′×1′分辨率的重力异常数据,结合EGM2008模型,采用移去-恢复技术计算大地水准面,位系数误差的影响可通过具体的模型误差来分析,这里暂且将它忽略。则截断误差主要包含两部分:
第一部分,是仅采用1′×1′重力数据计算大地水准面所造成的影响,即在整个球面上忽略了频段n=10 801~的重力数据而导致的高频截断误差:
(5)
其中,误差估计为:
(6)
第二部分,由于积分半径(球冠半径ψ0)以外区域采用的是2 160阶的EGM2008模型,相当于5′×5′的重力数据,也就是说,在该积分区域外还存在n=2 161~10 800的截断误差:
(7)
其中,误差估计为:
(8)
式中,Qn为截断系数,可表示为[7]:
(9)
研究推导Qn的文献很多。忽略其推导步骤,其计算式如下[7]:
(10)
式中,
Jn(ψ0)=
J0(ψ0)=I1(ψ0)
Kn+1(ψ0)-2Kn(ψ0)+Kn-1(ψ0)=
利用Rapp-Tscherning模型估计得重力异常阶方差为[8]:
(11)
式中,A=425.28,S=0.999 623,B=24,C2=7.5 (mGal)2。
根据式(6)和式(11),计算得到1′×1′重力数据分辨率造成的高频截断误差为0.63 cm。然后取不同的积分半径,依据式(8)~(11)计算积分半径外的截断误差,计算结果如表1所示。
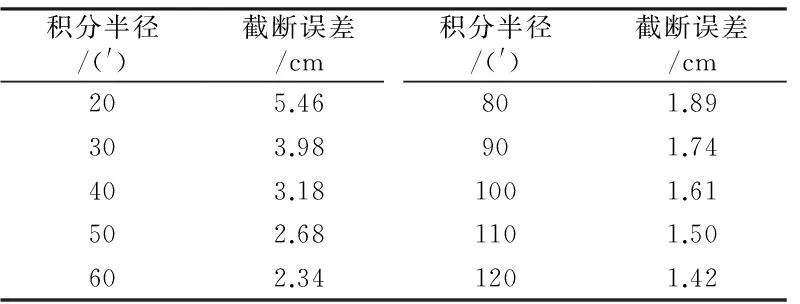
表1 不同积分半径造成的截断误差
3 不同地形区域重力场的谱特征
当利用式(6)、式(8)来估计分辨率以及远区高频截断部分造成的误差并以此确定平均重力异常积分半径时,是根据重力异常阶方差Cn估算的。而由式(11)给出的阶方差模型(以及其他一些已知模型)是国外学者通过全球重力异常的统计分析得出的经验公式,因此代表了全球重力异常的一般特征,但各个不同地区重力场的具体情况是有差异的。数据分辨率误差的本质是平均重力异常与其代表面积内各点重力异常的差异,即代表误差。对于局部地区,通常采用下面的代表误差模型[8]:
E2=4C2D
(12)
其中,D是平均重力异常矩形网格的边长,以km为单位;C称为代表误差系数,它与各地区的地形情况(反映了重力场的复杂度)有关。
由于
(13)
式中,角标K代表不同的地形类别。由代表误差的经验公式可见,不同地形类别的代表误差仅相差一个常数因子,故可取:
(14)
即
(15)
从而,可由C求得相应的常数AK:
(16)
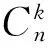
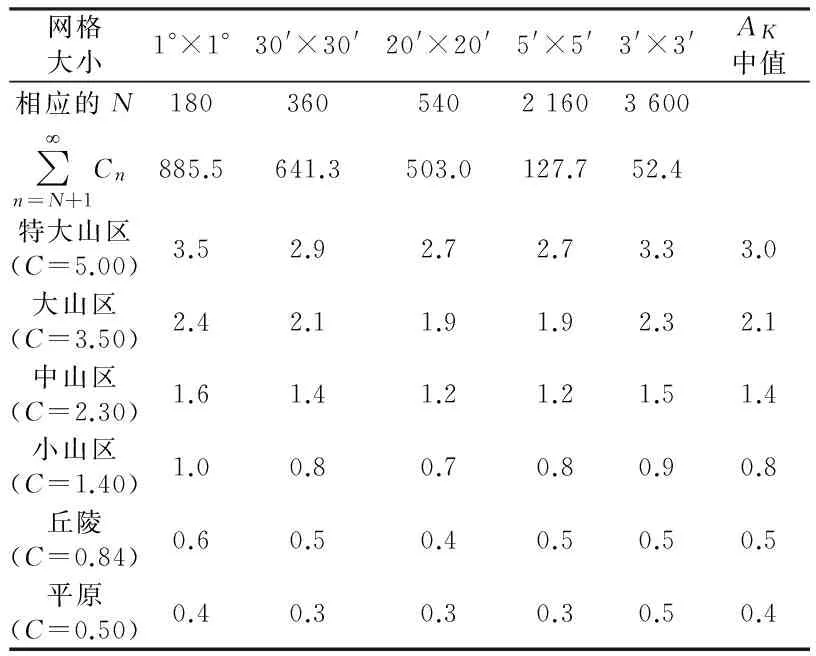
表2 不同地形区域AK统计
因而,考虑到不同的地形类别,式(6)与式(8)的高频截断误差分别变为:
(17)
(18)
根据式(17)计算的不同地形区域重力数据1′×1′分辨率造成的高频截断误差如表3所示。

表3 不同地形区域重力数据1′×1′分辨率
从表3可以看出,1′×1′数据分辨率造成的高频截断误差,即使在特大山区,也仅为1.88 cm,因此1′×1′重力数据分辨率能满足cm级大地水准面建模的精度要求。根据式(18)计算的不同地形区域不同积分半径造成的截断误差示于表4。
从表4可以看出,当积分半径取至20′时,在平原、丘陵和小山区均能满足cm级大地水准面建模的要求;但对于中山区与大山区而言,则积分半径至少需要取至30′和70′;而对于特大山区,积分半径即使取至2°也无法满足cm级建模的精度要求。继续扩大特大山区积分区域,结果示于表5。当积分半径取至3°时,在特大山区积分半径造成的截断误差为9.65 cm。
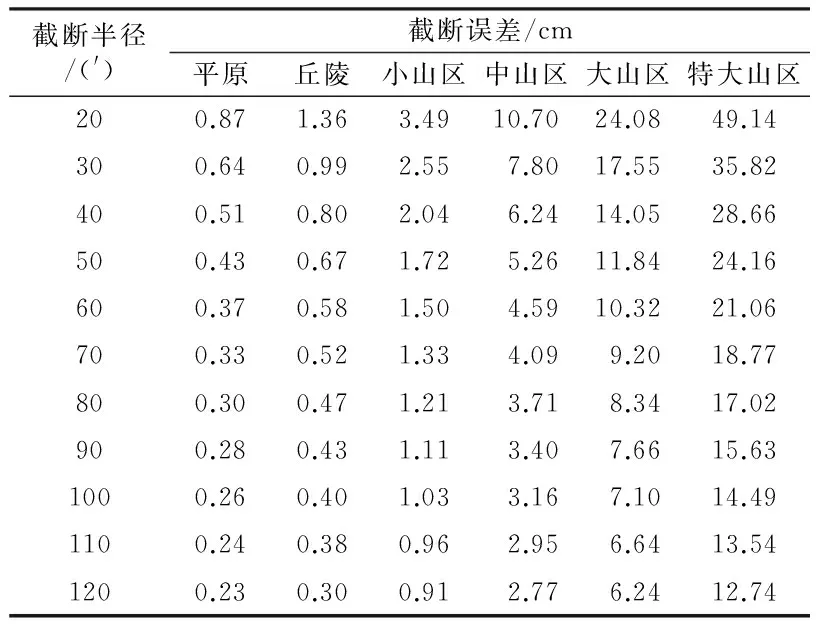
表4 不同积分半径在不同地形区域造成的截断误差
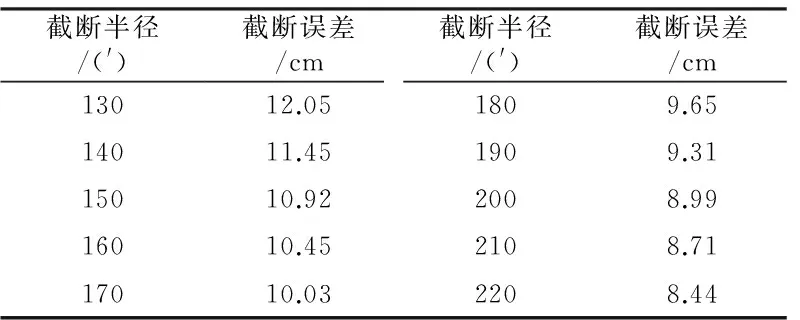
表5 不同积分半径在特大山区造成的截断误差
4 重力数据误差影响
仅考虑近区平均重力异常误差对大地水准面的影响,将式(3)表示为:
(19)
式中,S为线性化Stokes积分算子,δΔg为重力异常值向量。设平均重力异常的方差为CδΔg,根据误差传播定理,可得大地水准面的方差CδN为:
(20)
因此,平均重力异常中误差与大地水准面高中误差的关系为:
(21)
考虑到中央区S(ψ)的计算存在奇异问题,因此将式(20)表示为中央区σ0与扣除中央区σ-σ0的组合:
(22)
式中,MδN(σ-σ0)计算如式(21)。而在中央区,由于[6]
(23)
代入到式(1),得到平面近似下中央区大地水准面的计算公式[1]:
(24)
其中,
(25)
通过式(25),依据误差传播定理,将Δg(x,y)的误差传播给拟合系数aij,再通过式(24)计算MδN(σ0)。
选择不同积分半径计算3mGal、5mGal、10mGal以及20mGal平均重力异常误差对大地准面计算精度的影响,计算点位置(33°,110°),计算结果如表6所示(分辨率1′×1′,单位cm)。
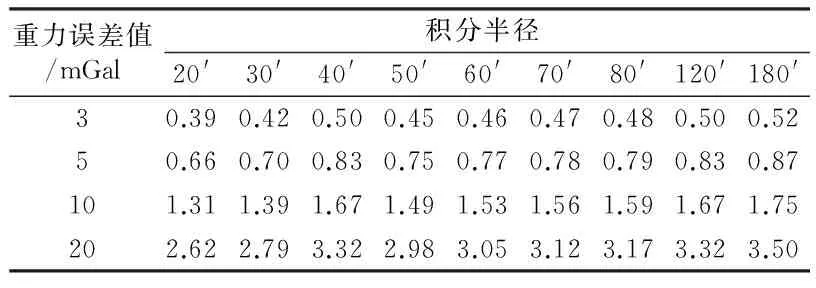
表6 不同积分半径平均重力异常数据误差
从表6可以看出,随着积分半径的增大,平均重力异常误差对大地水准面建模精度的影响逐渐增大。综合表3、表4与表6,我们可以根据局域大地水准面建模精度的要求,选择合适的积分半径,并对1′×1′平均重力异常精度提出要求。例如假定某计算区域为一大山区,要求大地水准面精度为10 cm,我们选定积分半径为80′,该区域1′×1′平均重力异常精度为10 mGal,则大地水准面建模精度为11.23 cm;如果该区域1′×1′平均重力异常精度为3 mGal,则大地水准面建模精度为10.12 cm。选定积分半径为120′,平均重力异常精度为10 mGal,则大地水准面建模精度为9.21 cm;如果该区域平均重力异常精度为3 mGal,则大地水准面建模精度为8.04 cm。显然,积分半径越大,平均重力异常精度越高,建模精度就越高。考虑到重力测量的工程量,在建立局域大地水准面模型之前,需要根据建模精度的需求选择合适的积分半径与平均重力异常精度,尽可能地满足建模精度需求,且测量任务又不至于过于繁重。
5 结 语
本文研究分析了1′×1′cm级大地水准面建模精度对不同地形区域积分半径选取以及平均重力异常精度的要求。实验表明,当积分半径取至20′时,在平原、丘陵和小山区均能满足cm级大地水准面的建模要求;对于中山区与大山区而言,则积分半径至少需要取至30′和70′;而对于特大山区,当积分半径取至3°时,其造成的截断误差为9.65 cm。同时,给出了3 mGal、5 mGal、10 mGal以及20 mGal平均重力异常误差对大地准面建模精度影响的量级大小。综合计算结果,我们可以选择合适的积分半径以及平均重力异常精度,使之既满足建模精度需求,又避免冗余繁重的工程测量任务。本文的研究成果对于计算确定局域cm级大地水准面模型具有参考价值与指导意义。
[1]李姗姗,吴晓平,张传定,等.顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J].测绘学报,2012, 41(4):510-516(Li Shanshan, Wu Xiaoping, Zhang Chuanding,et al. Regional Quasi-Geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly’s Gradient Term[J].Acta Geodaetica et Cartographia Sinica, 2012, 41(4):510-516)
[2]陈俊勇,李建成,宁津生,等.我国大陆高精度、高分辨率大地水准面的研究和实施[J].测绘学报,2001,30(2):95-99(Chen Junyong, Li Jiancheng, Ning Jinsheng, et al. On a High Resolution and High Accuracy Geoid in China Mainland[J].Acta Geodaetica et Cartographia Sinica, 2001, 30(2): 95-99)
[3]陈俊勇,李建成,宁津生,等.中国新一代高精度、高分辨率大地水准面的研究和实施[J].武汉大学学报:信息科学版,2001,26(4):283-289(Chen Junyong, Li Jiancheng, Ning Jinsheng, et al. A New Chinese Geoid with High Resolution and High Accuracy[J]. Geomatics and Information Science of Wuhan University, 2001, 26(4): 283-289)
[4]宁津生,罗志才,杨沾吉,等.深圳市1 km高分辨率cm级高精度大地水准面的确定[J].测绘学报,2003,32(2):102-107(Ning Jinsheng, Luo Zhicai, Yang Zhanji, et al. Determination of Shenzhen Geoid with 1 km Resolution and Centimeter Accuracy[J].Acta Geodaetica et Cartographia Sinica, 2003, 32(2): 102-107)
[5]Moritz H. Physical Geodesy [M]. New York:Springer-Verlag Wien, 2005
[6]郭俊义.物理大地测量学基础[M].武汉:武汉测绘科技大学出版社,1994(Guo Junyi. Foundation of Physical Geodesy[M]. Wuhan: Wuhan Techonology University of Surveying and Mapping Press, 1994)[7]Zhang C D , Lu Z L, Wu X P. Truncation Error Formulae for the Disturbing Gravity Vector[J].Journal of Geodesy, 1998, 72: 119-123
[8]陆仲连.地球重力场的理论与方法[M].北京:解放军出版社,1996(Lu Zhonglian. Theory and Method of the Earth’s Gravity Field[M]. Beijing: PLA Publishing House, 1996)
About the first author:LI Shanshan, PhD, professor, PhD supervisor, majors in physical geodesy, E-mail: zzy_lily@sina.com.
Effect of Error of Gravity Data on Geoid Determination
LIShanshan1QUZhenghao1
1Institute of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
Determining accurate regional geoid with Stokes theory can be affected by gravity data errors, such as resolution of gravity, precision of mean gravity and integral radius. In order to solve this problem, the magnitude of truncation errors of geoids in different terrain areas, which are caused by gravity resolution and integral radius, are given based on the analysis of characteristics of the gravity frequency spectrum. Also, the effect of error of mean gravity anomalies on geoid construction is calculated. Therefore, the results put forward in this paper contain great theoretical value for centimeter geiod calculation in different terrain areas.
truncation error; geoid; mean gravity anomaly; representation error; integral radius
National Natural Science Foundation of China, No.41274029; National High Technology Research and Development Program, No.2013AA122502.
2015-10-30
李姗姗,博士,教授,博士生导师,主要从事物理大地测量学研究,E-mail:zzy_lily@sina.com。
10.14075/j.jgg.2016.10.001
1671-5942(2016)010-0847-04
P223
A
项目来源:国家自然科学基金(41274029);国家863计划(2013AA122502)。
