有限元强度折减法在黄土路基边坡稳定分析中的应用

李 颖，梁 鸿，张 雷

（内蒙古农业大学能源与交通工程学院，内蒙古呼和浩特 010018）

道路工程

有限元强度折减法在黄土路基边坡稳定分析中的应用

李 颖，梁 鸿，张 雷

（内蒙古农业大学能源与交通工程学院，内蒙古呼和浩特 010018）

以解决实际工程中存在的黄土路基边坡的稳定性问题，本研究的主要思路是利用有限元软件ABAQUS，在有限元强度折减法的基础上，通过数值模拟边坡，对其稳定性进行分析，并且得到该边坡相应的稳定系数。模拟结果表明，对于黄土边坡存在的潜在破坏面，利用该法可以较为准确地、形象地预测其破坏位置与滑裂趋势，并且模拟得到的安全系数与简化的毕肖普法计算的结果很接近，不但增强了传统极限平衡法的计算结果的可靠性，也提高了精确性，还为评价黄土边坡的稳定性提供了新的方式。

ABAQUS；黄土边坡；边坡稳定性；强度折减法

1 引 言

准池铁路从内蒙古中部到山西省北部的重载运煤铁路专线。本线路的主要路基填料为黄土，通常黄土具有孔隙大、高压缩、低承载力、较差均匀性、遇水湿陷性等物理力学特性。因该地区主要分布的是新晋堆积的黄土，具有自重湿陷性质且密实度较低，且因此会对工程建设产生很大的影响。黄土边坡稳定性，是在路基工程建设中存在的一个重要的问题，同时，边坡稳定性也是至今尚未完全解决的经典力学问题之一，黄土边坡稳定性直接影响着黄土路基工程建设的安全问题，当黄土路基边坡出现变形、坍塌和滑坡等现象后会造成极其严重的工程事故。

近年来对于边坡稳定的研究，一直采用传统的极限平衡法，就简单剖面的均质边坡而言，从直观上采用极限平衡法一种比较便捷、准确地找到潜在破坏面的具体位置与大概轮廓的方法，从而确定稳定安全系数。在实际中，无论是人工边坡或是天然边坡，其主断面一般往往都呈现多级台阶，但在各种传统极限平衡法的理论基础上分析边坡稳定性时，对于土体内部的应力应变关系却没有充分考虑到，因而不能对非均质、非线性的不连续复杂地质土体进行描述和分析。有限元法不同于传统极限平衡法，它是一种能够对力的平衡条件、非均质边坡土体和不连续性、以及土体的应力、应变的大小和塑性分布都能充分考虑到的一种方法。与传统极限平衡法相比，有限元法的优点是可以避免将滑体视为刚体而过于简单，还可以通过计算机计算，对黄土边坡变形破坏机制根据应力、应变规律进行分析，使计算和分析的结果更加与实际情况相一致。

本文尝试利用大型有限元软件ABAQUS对准池铁路的黄土路基边坡进行计算机数值模拟，选取边坡的有限元分析方法——强度折减法，对边坡进行稳定性分析，将最后得到的安全系数与传统的毕肖普法的计算结果进行对比。结果表明，有限元强度折减法得到的稳定系数更偏于安全，同时说明强度折减法比传统的极限平衡法得到的结果更接近于实际情况，计算机模拟得到的塑形应变图可以较形象的描绘出边坡破坏的情况，今后将该方法应用于对黄土边坡稳定性的分析研究之中。

2 有限元强度折减法理论概述

2.1折减强度法原理

有限元强度折减法的基本原理是，基于假定外荷载始终保持不变以其他外部条件不变的情况的条件下，将边坡土体的两个主要强度参数：粘聚力c和摩擦角tanφ分别除以一个折减系数值F，得到新一组的强度参数c′和φ′

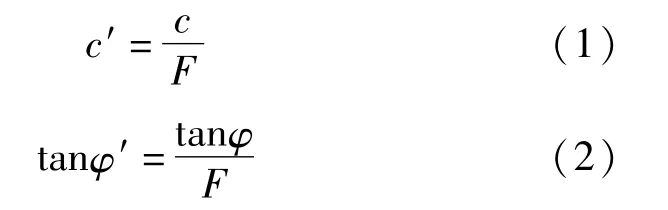
计算后会得到新的材料参数c′和φ′，将新的强度参数再次输入所建立的原始模型中，数值改变后，重新进行有限元计算。然后通过不断增大或减小折减系数F的值，反复代入进行试算，直到有限元的计算不再收敛。当有限元计算不收敛，说明这时的边坡发生剪切破坏，达到临界极限状态，即边坡土体抗剪强度将达到最大值，得到破坏滑动面和塑性应变区，此时对应的折减系数F的值即为边坡的安全系数。

传统极限平衡法采用的是Mohr-Coulomb屈服准则，其安全系数的定义是：沿着滑移面的抗剪强度与滑移面上实际剪应力之比，表示为

将式（3）两边同时除以Fs得

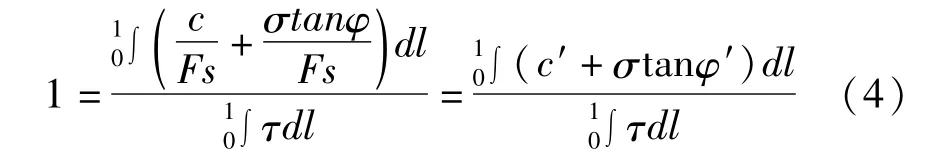
得到式（4）左边等于1，这时的强度参数为Fs，边坡处于临界状态。由此可以看出，虽然有限元强度折减法与传统的极限平衡法的计算方式略有不同，但在本质上二者的基本理论是一致的。

2.2有限元分析软件ABAQUS

本文采用目前在处理岩土工程问题时应用较广的大型有限元分析软件ABAQUS，对边坡进行计算机数值模拟，该软件不仅涵盖了大量的针对不同材料的各种模型，还能模拟土体这种复杂又特殊的材料，特别是它的非线性分析功能和良好的收敛性，在解决复杂的岩土力学的非线性问题方面优势显著。ABAQUS能够真实的反映土体复杂性状的本构模型，进行土体中应力、应变、位移的计算，因此，在岩土工程领域有广泛的应用。

（1）屈服准则的选取

土体的抗剪强度是衡量土坡失稳破坏的关键影响因素之一，当图特的剪应力达到极限破坏状态时，土坡随之失稳。故本文在用强度折减法处理黄土边坡稳定问题时，采用理想弹塑性模型进行建模，屈服准则设定为Mohr-Coulomb屈服准则：F=

式中：I1和J2分别为应力的张量第一不变量和偏量第二不变量；θσ为应力罗德角，且

（2）流动法则

在ABAQUS中采用的摩尔-库伦准则中引入了流动势函数，使其屈服面光滑，以便于计算。流动法则其描述了土体材料进入塑性阶段后的应力和应变之间的关系，与Mohr-Coulomb屈服准则相对应的塑性势函数为：

式中：σm为平均应力；ψ为剪胀角，且0≤ψ≤φ。当ψ=0不会出现剪胀现象，当ψ=φ符合Mohr-Coulomb准则的屈服条件，出现最大的剪胀现象。根据黄土的特性，采用非关联流动法则，即剪胀角ψ=0。

2.3边坡稳定的评判依据

对于利用计算机数值模拟边坡稳定，其判断边坡失稳的主要依据有三种：第一，有限元的解是否收敛性，当有限元的解不再收敛时，边坡失稳；第二，以计算不收敛为标准、最大位移与折减系数三者之间的曲线变化特征，边坡失稳时三者的曲线变化会有明显的突变点；第二，以特征点位移突变为标准、塑性区是否贯通为标准，当塑性应变区从坡脚贯穿到坡顶时，边坡失稳。这三种失稳判断依据都存在一定的局限性，各有利弊，本文采用塑性区贯通作为边坡失稳的判断依据，从而对黄土边坡进行稳定性的分析。

3 ABAQUS建模

本论文使用的ABAQUS版本为6.11，为了更好的了解黄土边坡稳定性问题，选择路基上一侧的黄土路基边坡为模拟对象。按照平面应变建立有限元的边坡模型，几何模型的边坡边界条件设定为左、右两边水平约束，即Ux=0。底面为水平横向和垂直纵向都约束的铰接约束，即Ux=0，Uy=0。坡顶上部为自由边界。黄土的本构模型选用弹塑性模型，屈服准则为Mohr-Coulomb屈服准则。采用非关联流动法则，即剪胀角ψ=0。

该地区黄土属于IV区—山西地区黄土，因该地区主要分布的是新晋堆积的黄土，密实度较低，因此会对工程建设产生很大的影响。通过室内实试验得到，该路基黄土边坡的最大干密度是1.83 g/cm3，最佳含水率是12.4％，烧灼失量是4.02％。

对黄土边坡进行ABAQUS计算机建模，其中该边坡的尺寸取总宽度28 m，深度20 m，黄土边坡的土体主要分为三层，具体尺寸如图1所示。对该沿线进行勘探后，经过分析和试验得出的土层主要模型物理力学参数如表1。

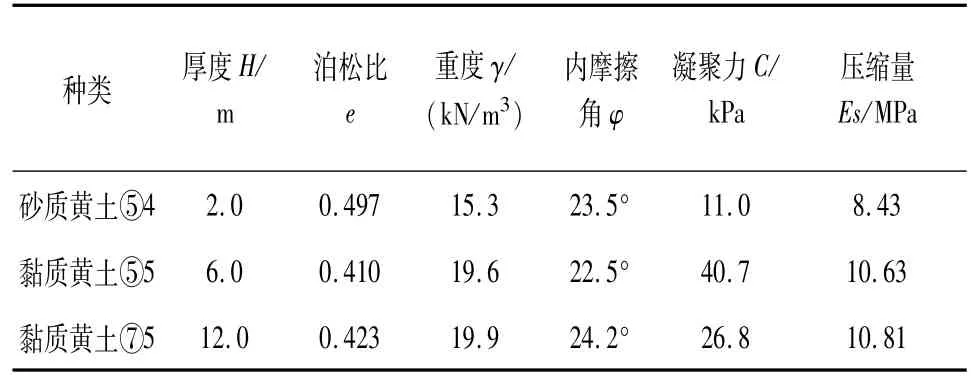
表1　模型各物理参数取值

图2是ABAQUS经过创建模型、定义截面属性、创建分析步、定义边和荷载、划分网格等步骤之后的黄土路基边坡模型，黄土路基边坡的网格划分采用八节点四边形平面应变孔压单元（CPE8P）。

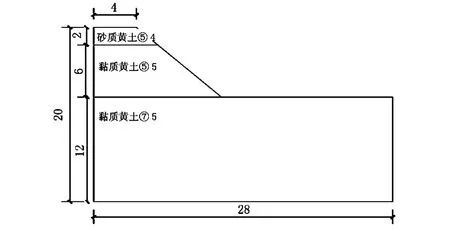
图1　模型尺寸图

图2　黄土路基边坡模型

经过ABAQUS/Standard计算之后，图3为黄土路基边坡在折减系数F=1.0时初始状态的塑性应变云图，此时的黄土边坡处于稳定状态。

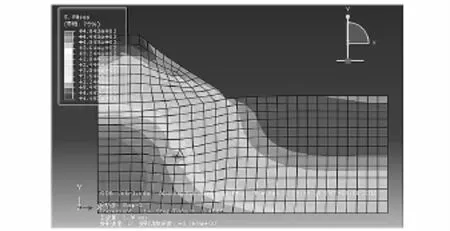
图3 F=1.0时塑性应变图

图4-6中，可以明显看到剪应力的扩展趋势，当不断改变折减系数将其增大时，剪应力也随着折减系数的增加而增大，从坡脚开始，塑性应变区逐渐扩大，对应着黄土边逐渐的破坏过程。在图5中塑性应变区有明显的从下向上延伸扩大的趋势，当折减系数F=1.26时，从图6中可见边坡上的塑性应变区已连成一片，但此时，边坡仍呈稳定状态。

图4　F=1.2时塑性应变图

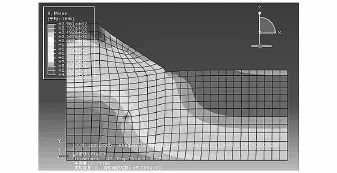
图5　F=1.25时塑性应变图

图6　F=1.26时塑性应变图

图7　F=1.27时塑性应变图

由图7可知，当强度折减系数F增加到1.27时，从图上可以直观看到坡角塑性区正往边坡顶面发展，并且在边坡形成贯通区域，，位移也在增加。当折减系数F=1.28时，有限元计算不收敛，认为边坡处于失稳状态。从而判定通过ABAQUS软件模拟得到的黄土边坡临界状态时的安全系数为1.27，此时边坡处于临界破坏状态。模拟结果的得到的安全系数1.27与简化毕肖普法算出的安全系数1.30很接近，这表明强度折减法在处理黄土边坡稳定性问题上是合理、可行的。此外，从图7中可以清楚看到黄土边坡的塑性应变是由下而上，从坡角开始逐步向坡顶的扩展趋势。应用该方法不但可以简便地得到边坡的安全稳定系数，还可以看到临界破坏时的滑裂面在塑性应变图上是直观的，容易被判别的。

4 结 论

本文在分析黄土边坡稳定性时利用了ABAQUS软件求解非线性的功能与强度折减有限元法，利用计算机模拟黄土边坡的状态与实际情况相结合，通过ABAQUS模拟对黄土边坡进行计算，得到的动态显示技术为黄土边坡的真实受力状态提供参考依，形象地预测出黄土边坡失稳时的破坏趋势。分析表明，本文运用强度折减法所确定的安全系数，通过与简化Bishop法计算所得安全系数的对比，发现二者的安全系数值极为相近，且两者的计算误差在合理的误差范围之内，所有可将此法引用在准池铁路的黄土边坡稳定性分析中是合理可行的，同时也为解决黄土边坡稳定性的问题提供一定的理论支撑和施工依据。

［1］ 王永焱.中国黄土的结构特征及物理力学性质［M］.北京：科学出版社，1990：15-17.

［2］ 崔月娥.关于黄土湿陷敏感性问题探讨［J］.煤炭工程，2010，（8）：76-78.

［3］ 史宏民.湿陷性黄土工程性质及其地基处理方法简述［J］.山西水利，2010，（2）：47-48.

［4］ 张丽萍.有限元强度折减法验算黄土高路堤边坡稳定性［J］.西部探矿工程，2007，（5）：4-3.

［5］ 张鲁渝，郑颖人，赵尚毅，时卫民.有限元强度折减系数法计算土坡稳定安全系数的精度研究［J］.水利学报，2003，（1）：21-7.

U418.9

C

1008-3383（2016）09-0001-03

2016-03-27

李颖（1989-），女，内蒙古呼和浩特人，硕士研究生，从事道路工程相关工作研究。

重载铁路黄土路基冲击压实机理与质量控制研究（207-003）。