朔黄线重载列车节能策略的设计与实现

程　伟，陈临强，郑木火

(1.杭州电子科技大学计算机学院，浙江 杭州 310018;2.浙江浙大网新集团，浙江 杭州 310052)



朔黄线重载列车节能策略的设计与实现

程伟1，陈临强1，郑木火2

(1.杭州电子科技大学计算机学院，浙江 杭州 310018;2.浙江浙大网新集团，浙江 杭州 310052)

朔黄线路条件复杂，重载列车在该线路上行驶时，一直以来未考虑节能问题.根据朔黄线路条件，从操纵优化角度给出了该线路下坡行车的节能策略.在相同路况下，速度波动越低，平均速度越小，越节能；平均速度基本相同时，制动距离越小，越节能.在满足安全、准点的前提下，可实现节能5%以上，为列车折返存储更多电量.

朔黄线路；节能策略；操纵优化；重载列车；存储电量

0　引　言

轴重30 t以上煤炭运输重载铁路关键技术与核心装备的研制有利于提高重载运输和创新能力.目前，对大运量重载列车节能的研究主要围绕列车节能运行的技术操作层面展开，比如以列车动力系统为研究对象的牵引动力优化研究[1].而从操控方式角度研究重载列车节能策略，一般是借鉴传统行车经验，以最大加速度启动，以最大减速度降速或停车，增加行车过程中的惰行时间，这在地势较平坦的铁路上确实取得了较好的节能效果[2-3].但朔黄线多以大下坡为主，线路条件复杂，起点至终点的垂直高度差近2 km，运行区间内一味增加惰行时间会引起列车超速，安全隐患极大.本文提出了基于朔黄铁路实际路况的节能策略，为朔黄线上重载列车节能运行提供了一种标准，具有一定的经济价值和现实意义.

1　坡度划分

根据对朔黄线路条件的分析发现，坡度是造成朔黄线能耗大的主要线路原因.如何根据朔黄线条件设计节能策略，得到能耗优化值是本文研究重点.朔黄全线近600 km，34个站.图1(a)给出了全线起点至终点高度差示意图，图1(b)给出了全线运行工况示意图，图中上/中/下3段分别表示制动、惰行、牵引工况，图1(c)给出了全线运行时的管压变化情况.

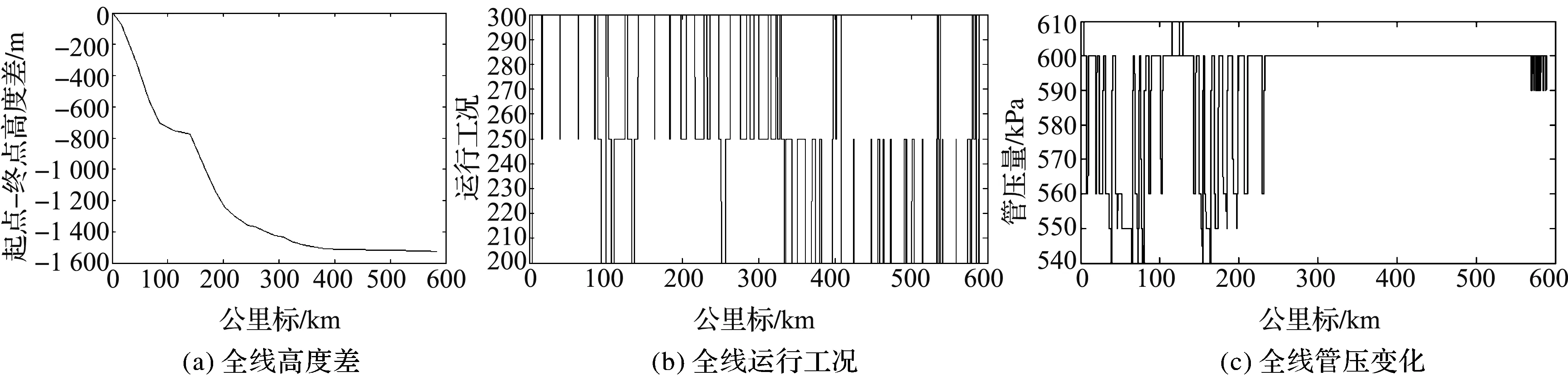
图1　朔黄全线列车运行概况图

由图1可看出，管压量变化明显地方均是在坡度较陡处，因该处(0～240 km)需施加空气制动；坡度较缓处(240～320 km)管压量无变化，是以电制动为主的运行工况；平坡上(320～580 km)，主要以牵引为主.根据图1所示线路状况以及运行工况，将全线划分为有空气制动做功的长大下坡、以电制动为主的大下坡以及以牵引为主的平坡起伏坡道.

2　能耗模型设计

2.1长大下坡

长大下坡段需要施加空气制动，图2给出了机车在该区间运行的最小简化模型，A-B为长大下坡，需施加空气制动，B-C为平坡.

图2　需空气制动的产电模型

根据能量守恒定律，列车从A点运行到C点有：

E0+Es=En+Ee+Ez+Ep.

(1)

式中：E0，Ee为列车在A，C两点的动能；En为从A点到C点电制动做功；Ez为从A点到C点基本阻力做功；Es为列车在A点的势能；Ep为从A点到C点空气制动力做功.故制动能耗为：

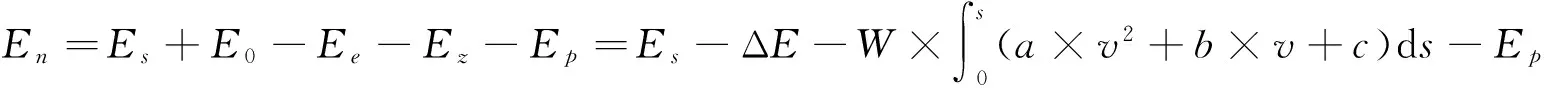
(2)

式中：a，b，c为与车辆类型有关的常数.根据《列车牵引计算规程》，以朔黄线上的主力机车HXD1型为例，列车基本阻力F=0.000 3 v2+0.038 v+1.4，v为当前列车速度[4].ΔE为动能变化量，W=m×g，m为列车质量，g为重力加速度9.806 65N/kg.

结合式(2)，在初始势能Es确定且已知前提下，En的优化值与ΔE,Ez,Ep有关，从式(2)得出如下结论：

1)空气制动做功相同时，速度越低，电能产量越多；

2)速度相同时，空气制动做功越少，电能产量越多.

考虑实际线路运行条件，本文主要分析了结论2，Ep=f×s，其中f为空气制动力大小，s为空气制动距离.因此，在保证安全，准点条件下，减少f或s均可减少空气制动做功，增加电能产量.

2.2大下坡

朔黄线上从第12站到第18站以0.4%～0.6%的大下坡为主，该区间以电制动为主.图3给出了机车在该区间运行的最小简化模型，A-B为坡度在0.4%以上，0.6%以下的大下坡，B-C段为平坡.

图3　电制动为主的产电模型

根据动力学定律，列车从A点运行到C点有：

Es+E0=En+Ez+Ee.

(3)

式中：E0,Ee为列车在A，C两点的动能；En为从A点到C点电制动做功；Ez为从A点到C点基本阻力做功；Es为列车在A点的势能.故

En=Es-ΔE-Ez.

(4)

式中：ΔE为动能变化.在A点的势能确定情况下，根据式(4)可知：

1)列车牵引能耗值与其运行速度有关；

2)列车运行速度越低，动能变化越小，基本阻力耗能越小，从而再生制动产生电能越多.

2.3平坡起伏坡道

结合朔黄线的实际路况，当坡度小于0.4%时，以起伏坡道为主，这在18站之后比较常见，图4给出了机车在第18站之后运行的最小简化模型.

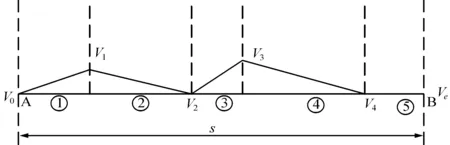
图4　平坡上的起伏坡道

列车从A点运行到B点，设①，③，⑤段施加牵引，②，④段施加制动，则在5个区段运行的能耗分别为：

E1=EV1+W×H1-EV0+Ef1,E2=EV2-W×H2-EV1+Ef2,E3=EV3+W×H3-EV2+Ef3,

E4=EV4-W×H4-EV3+Ef4,E5=Ee-W×H5-EV4+Ef5.

所以总的能耗为：

E=E1+E2+E3+E4+E5=Ef1+Ef2+Ef3+Ef4+Ef5+W×ΔH+EVe-EV0.

(5)

式中：ΔH为A站和B站之间的高度差；Ef1～Ef5为列车的基本阻力所消耗能量；EVe,EV0～EV4为列车动能；E1，E3，E5为列车牵引能耗；E2，E4为列车制动产能.

总能耗可转化为：

(6)

式中：ΔE为动能变化量，同时W×ΔH是确定的，那么列车能耗的优化就是基本阻力能耗和动能变化量的寻优问题.得到如下结论：

1)列车能耗的优化值即为基本阻力能耗和动能变化量的优化值；

2)列车运行速度越低，则牵引所消耗的能量越小.

3　平坡起伏坡道上的节能算法

结合朔黄线路条件.在坡度小于0.4%时，可匀速或非匀速(惰行)控车[5].此区间的非匀速行车指在最大限速和最小速度区间内惰行，当速度超过最大限速则施加制动，低于最小速度则施加牵引.下面将从理论上对比匀速和惰行行车能耗情况.前提条件为：

图5　匀速-非匀速v -t图

1)A站到B站运营时间相同，时间为T；

2)为简化计算量，设A站和到B站的速度相同，并且等于匀速运行的速度；

3)A站到B站的距离为s.

列车匀速和非匀速的速度-时间曲线如图5所示，MRSP曲线表示最大限速，点划线表示非匀速(惰性)，实线表示匀速.

设T时刻，运行位移相等，故s1=s2，设初速度v0，s1速度变化率Δv1，s2速度变化率Δv2，其中：

1)s=s2+s3+s4=s1+s3+s4=v0×t；

2)由s1+s3=(v0+Δv1)×t1得出s1=(v0+Δv1)×t1-s3=Δv1×t1；

3)s4=(v0-Δv2)×(T-t1)；

4)由s2+s4=v0×(T-t1)得出s2=v0×(T-t1)-s4=Δv2×(T-t1).

所以得到：

1)如果t1=T/2,Δv1=Δv2；

2)如果t1>T/2,Δv1≤Δv2；

3)如果t1Δv2.

因始末速度相等，结合式(6)，得到：

1)列车匀速运行时：

W×F0×s+W×ΔH.

(7)

2)列车非匀速运行时：

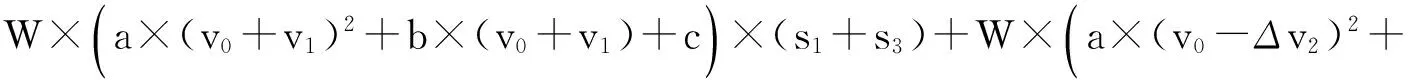
s4+W×ΔH=W×F0×s+W×ΔF1×(s1+s3)-W×ΔF2×s4+W×ΔH.

(8)

式中：F0为匀速运行的单位基本阻力，ΔF1，ΔF2是与Δv1，Δv2对应的单位基本阻力变化率，式(8)减式(7)得能耗差ΔE：

ΔE=W×ΔF1×(s1+s3)-W×ΔF2×s4=W×ΔF1×(v0+Δv1)×t1-W×ΔF2×

(v0-Δv2)×(T-t1).

(9)

针对不同的t1值以及Δv1，Δv2，分析速度波动与能耗的关系：

1)如果t1=T/2,Δv1=Δv2，则有

ΔE=W×(ΔF1-ΔF2)×v0×T/2+W×(ΔF1+ΔF2)×Δv1×T/2>0，所以匀速控车更节能；

2)如果t1>T/2,Δv1≤Δv2，则有

ΔE=W×ΔF1×(v0+Δv1)×t1-W×ΔF2×(v0-Δv2)×(T-t1)>

W×ΔF1×(v0+Δv1)×t1-W×ΔF2×(v0-Δv2)×t1=

W×(ΔF1-ΔF2)×v0×t1+W×(ΔF1+ΔF2)×Δv1×t1.

如果Δv1≥v0，那么ΔE>=W×(ΔF1-ΔF2)×v0×t1+W×(ΔF1+ΔF2)×v0×t1>0，说明波动越大，能耗越多，匀速控车速度波动为0，更节能；

3)如果t1Δv2，则有

ΔE=W×ΔF1×(v0+Δv1)×t1-W×ΔF2×(v0-Δv2)×(T-t1)>W×ΔF1×(v0+Δv2)×t1-

W×ΔF2×(v0-Δv2)×t1>0，说明匀速控车更节能.

综上所述，列车在起伏坡道区间行驶时，在保证安全，准点前提下，因尽量减少速度波动，降低速度，这样有利于提高能量利用率，达到较好的节能效果.

4　仿真验证

仿真环境搭建在独立的PC机上，由sim程序和TOD程序组成，通过设置主机IP来模拟sim和TOD的IP，启动sim仿真，通过UDP协议实时向TOD发送线路数据.TOD程序根据当前速度，线路状况决定施加牵引/制动力的大小.根据做功—电能转化关系式1 kW·h=3.6×106J，得到相应的电能情况.

4.1空气制动距离验证

长大下坡段的龙宫—北大牛区间基本是施加一次空气制动.在保证区间平均速度基本相同时，图6给出了该区间两次空气制动的位移关系图，可以看出，实线的减压量与虚线减压量相同，而制动距离更小.图7给出了空气制动区间的能耗对比情况，负数表示发电，正数表示耗电.结合图6、图7可发现，在减压量相同时，制动距离小的实线发电量明显高于制动距离大的虚线发电量.

图6　两次空气制动下的位移对比图

图7　两次空气制动下的能耗对比图

4.2速度大小验证

目前，大下坡段的西柏坡—三汲之间运行速度在60～70 km/h之间，运行时间小于规划时间，在满足准点的条件下，图8给出了该区间的两条速度曲线，图9给出了不同速度下该区间的能耗情况.图8中，虚线代表的速度大于实线表示的速度，结合图9看出，虚线的能耗明显高于实线的能耗.

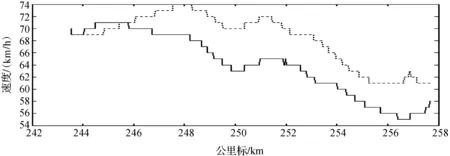
图8　速度曲线图

图9　不同运行速度的能耗对比图

4.3速度波动验证

图10给出了朔黄线平坡起伏坡道上太师庄—河间区段的两种运行工况，实线速度波动范围较小，维持在区间[66,68]内，可认为匀速；虚线的速度波动较大，代表非匀速(惰行).图11给出了两种运行工况下该区间的耗电量情况，两条曲线均成线性关系递增，表明该区间主要是牵引做功，能耗不断累加.图10中虚线相对实线的速度波动明显，结合图11，虚线的耗电量大于实线耗电量.从而验证了速度波动对能耗的影响.

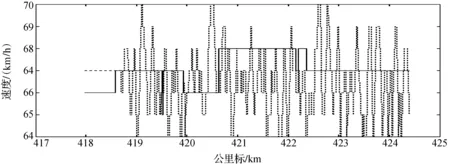
图10　不同速度波动图

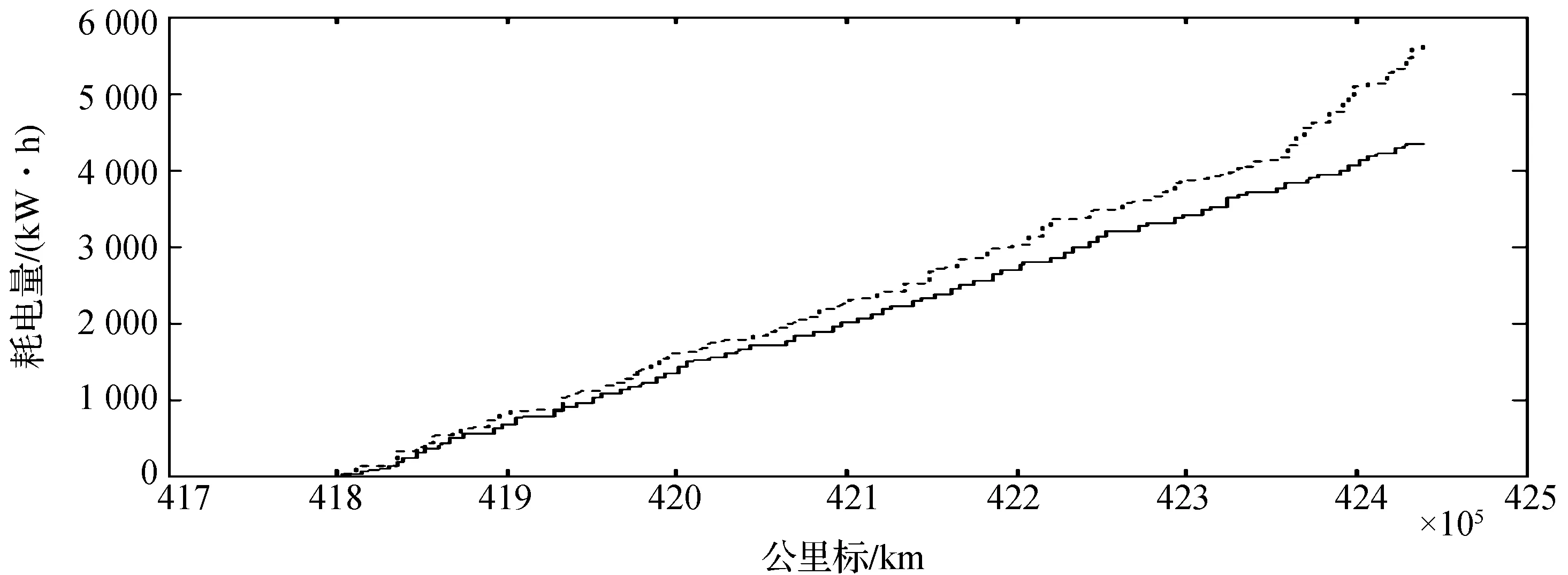
图11　不同速度波动下的能耗对比图

自此，针对朔黄线长大下坡的空气制动节能策略、大下坡的速度节能策略、平坡上起伏坡道上的速度波动节能策略均得到仿真验证.针对上述区间，图12给出了采用节能优化策略前后的能耗曲线.

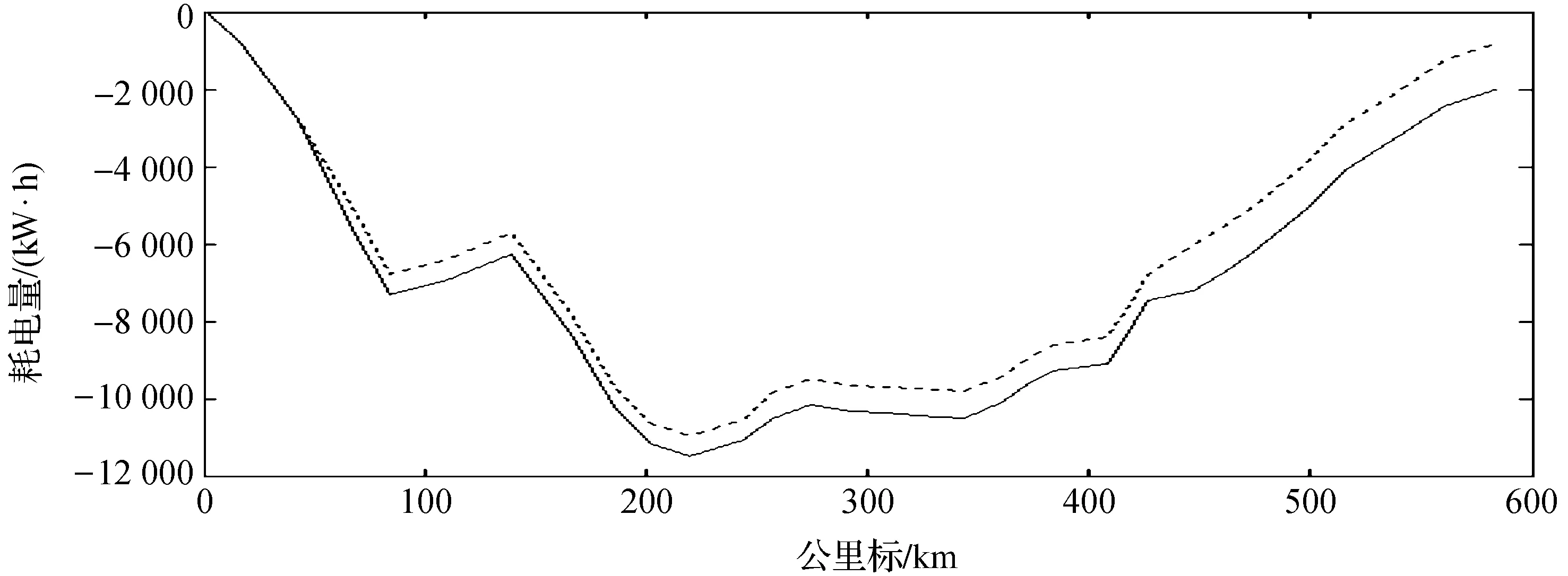
图12　采用节能策略前后能耗比较图

可以看出，上述3个区间采用节能优化策略后，发电量明显增多.万吨重载列车在朔黄全线运行一趟，耗电约13 000 kW·h，结合图12优化后曲线，以节电1 000 kW·h计算，节能率1 000/13 000×100%=7.6%，大于5%的节能指标.如果在保证安全，准点前提下，其他区间也按该节能策略进行，则节能效果会更明显.本节能策略实现了科技支撑项目要求的节能指标，为列车折返爬坡储存了更多电量，也为开展20 000 t列车的节能策略提供了重要借鉴思路.

5　结束语

本文以朔黄铁路重载列车为研究对象，通过建模，设计适用于该线路上的节能策略，并应用在30 t轴重列车上，在仿真环境下验证了该策略的正确性，可行性.为朔黄铁路上的重载列车节能问题提供了一种切实可行的方案，并为后续智能操控辅助驾驶曲线的优化从节能角度提供了一种思路.如何在辅助操控曲线中，根据前方路况信息，结合节能策略，自动优化曲线，降低能耗，是后续研究的重点.

[1]薛艳冰,马大炜,王烈.列车牵引能耗计算的实用方法研究[C]//铁道科学技术新进展铁道科学研究院五十五周年论文集,北京:中国铁道出版社，2005:665-669.

[2]丁雪松.城市轨道交通列车节能优化及能耗评估[D].北京:北京交通大学，2012.

[3]付印平，李克平.列车运行节能操纵优化方法研究[J].科学技术与工程，2009,9(5):1337-1340.

[4]王问盈.我国《列车牵引计算规程》的回顾与前瞻[J].铁道机车车辆,2000(1):7-10.

[5]钱立新.世界铁路重载运输技术[J].中国铁路，2007(6):49-53.

Design and Implementation of Energy-saving Strategies of Load Train of Shuohuang Railway

CHENG Wei1, CHENG Lingqiang1, ZHENG Muhuo2

(1.SchoolofComputer,HangzhouDianziUniversity,HangzhouZhejiang310018,China;2.ZhejiangInsigmaGroup,HangzhouZhejiang310052,China)

Because of complex conditions of Shuohuang line, load train on this line is not considered a problem about energy efficiency. According to Shuohuang line conditions, given from the steering angle to optimize traffic on the line energy policy, concluded in the same road, lower volatility of speed, smaller of average speed, more energy-efficient; substantially the same average speed, smaller of braking distance, more energy-efficient. To meet the safety, punctuality premise, more than 5% energy can be achieved, and more energy can be saved when train return.

Shuohuang railway; energy conservation; manipulation of the optimization; overloaded train; stored energy

10.13954/j.cnki.hdu.2016.05.007

2015-12-07

国家科技支撑计划资助项目(2013BAG20B01)

程伟(1991-)，男，安徽黄山人，硕士研究生.智能控制.通信作者：陈临强教授，E-mail：clq@hdu.edu.cn.

U284.48

A

1001-9146(2016)05-0031-07