韭园沟流域淤地坝坝系布局评价

王 丹,李占斌,李 鹏,高海东,赵宾华,袁水龙

(西安理工大学 西北水资源与环境生态教育部重点实验室,西安 710048)



韭园沟流域淤地坝坝系布局评价

王 丹,李占斌,李 鹏,高海东,赵宾华,袁水龙

(西安理工大学 西北水资源与环境生态教育部重点实验室,西安 710048)

淤地坝系的科学布局关系到流域的防洪安全，对淤地坝系布局进行评价，可以为流域坝系工程的规划、建设和设计工作提供理论依据。将黄土丘陵沟壑区韭园沟流域划分为1个主沟坝系单元和14个子坝系单元，选取了大型坝占总比、串联率、库容均衡度、稳定系数、侵蚀模数、洪量模数及保收率7个指标，采用AHP、IAHP、熵权法及组合权重法分别计算了各指标权重，依次对韭园沟坝系布局进行了评价。研究表明：(1)流域部分子坝系单元布局不合理，但全流域坝系布局合理；(2)IAHP法和组合权重法在计算权重时更客观，评价结果较为合理；(3)4种方法中，大型占总比权重系数均达到最大，表明骨干坝对坝系布局有决定性影响；(4)当骨干坝控制全流域50%以上，库容均衡度达0～20万m3/km2，稳定系数达到1/25～1/20，洪量模数0～10万m3/km2，骨干坝串联个数低于2.5座/km时，坝系布局基本合理。

坝系单元; IAHP; 熵权法; 组合权重; 坝系布局评价

长期的水土保持实践表明，淤地坝在黄土高原地区水土流失防治中是最行之有效的沟道工程措施。淤地坝的显著特点是能有效地拦截洪水泥沙，集大面积水肥于小地块利用，形成高产稳产的基本农田，从而有效实现了治黄与治贫、生态环境建设的长远利益和经济发展的现实利益等基本关系的协调发展[1]。在黄土高原水土保持治理长河中，其巨大的经济、生态和社会效益已得到广泛认可。

近年来，为确保发挥淤地坝的安全效益和整体效益，基于前人的研究经验和试验基础，单元控制理论即“小流域为单元，骨干坝为支架，骨干坝和中小型淤地坝相嵌套”的建坝思路逐渐形成[2]。正是在骨干坝以及中小型坝的配合分工和联合运用下，小流域的水沙利用能力才得以提高。而流域坝系总体布局的合理与否，决定着坝系工程充分发挥其系统功能的成败。不合理的坝系布局可能对工程自身以及下游的安全，乃至水沙资源的持续利用造成影响。因此，为给小流域坝系工程的规划、建设和设计工作提供理论依据，以期实现小流域坝系建设项目效益的正常发挥，对小流域坝系总体布局合理性进行的评价工作就显得尤为必要。

目前，已有众多学者对坝系布局合理性评价系统进行了初探。陈骞[3]在小流域坝系建设的问题探讨中强调了土壤侵蚀模数的确定在淤地坝系布局研究中的重要性；蒋耿民[4]引入模糊数学理论，采用多层次模糊综合评价模型对淤地坝坝系工程总体布局的综合评价数值进行了具体计算，初步实现了淤地坝坝系工程总体布局多目标、动态的综合评价效果。然而，目前针对小流域坝系总体布局合理性开展的评价工作还存在诸如评价指标不明确、定性多于定量的缺陷[5]，因而难以得到科学合理的布局评价效果，不能适应黄土高原水土保持淤地坝工程建设的需要。本文选取黄土高原水土保持工程典型示范区——韭园沟流域为研究对象，综合考虑经济、安全及效益等各方面因素选取并建立适当指标，构建布局评价系统，对该流域淤地坝系进行布局评价研究，以期为小流域坝系工程的规划、建设和设计工作提供理论依据。

1　数据与方法

1.1研究区概况

韭园沟流域地处陕西省绥德县，属于黄土丘陵沟壑丘第Ⅰ副区，为无定河中游左岸一级支流，地理位置位于东经110°16′—110°26′，北纬37°33′—37°38′，是黄河中游多沙粗沙主要来源区的代表性小流域。主沟长18 km，平均比降1.15%，沟道断面呈“V”字形，沟壑密度5.34 km/km2，海拔高程820～1 180 m。流域内地形破碎，沟壑纵横，梁峁起伏，土层深厚，土地贫瘠，植被稀少，垦殖指数高，水土流失严重，平均土壤侵蚀模数达到14 000 t/(km2·a)，属于无定河中下游丘陵沟壑强度流失区。韭园沟流域地处温带半干旱地区，年蒸发量1 519～1 600 mm，多年平均降水量为469 mm，雨水多集中在7—9月，且多数以暴雨形式出现。

韭园沟流域沟道坝系经过多年的示范建设，截至2010年底，水土保持措施面积4 832.8 hm2，其中基本农田、林地、草地面积分别为1 613.6，2 383.9，835.4 hm2，治理程度达到68.9%。全流域淤地坝共计257座，总库容达3 016.1万m3，已淤库容2 695.6万m3。其中，骨干坝24座，总库容为2 111.5万m3，已淤库容1 648.6万m3，平均单坝控制面积4.38 km2；中型坝47座，总库容为850.3万m3，已淤库容722.8万m3，平均单坝控制面积0.98 km2；小型坝186座，总库容为407.5万m3，已淤库容324.2万m3，平均单坝控制面积0.18 km2。全流域布坝密度为3.7座/km2，总库容43.0万m3/km2，已淤库容38.5万m3/km2，可淤地面积5.4 hm2/km2，已淤地面积4.4 hm2/km2，人均坝地0.026 hm2。坝地面积与坝控面积之比达到1/24，坝系进入基本保收阶段[6]。

1.2技术路线

1.2.1流域坝系单元的划分小流域坝系一般包含若干个相对独立的子坝系，而子坝系又是构成总坝系的基础单元。子坝系在总坝系群体联防中，独当一面，镇守一方，同时通过其防洪、淤地、生产功能的有机结合与分工负责以及对下游坝系的控制作用，保障了下游流域坝系的生产安全与功能发挥。韭园沟流域坝系的Ⅲ级沟道具有较合理的布坝条件和结构，易形成坝系单元。本文根据该流域坝系现状分析，按照坝系单位划分要求，将整个流域坝系划分为1个主沟坝系单元和14个子坝系单元，并分别以各坝系单元以及全流域为研究对象展开布局评价工作。韭园沟内部各坝系单元间的控制与从属关系见图1。

1.2.2评价指标的建立与计算淤地坝坝系工程总体布局是一个涉及因素多、涉及范围广的复杂系统，对其实现比较深入、全面的评价是非常困难的。建立科学合理的评价指标体系，是影响评价结果准确性和客观性的关键。本文基于相关领域专家学者以往的研究成果，并结合淤地坝工程实际，综合考虑防洪安全、稳定可靠以及经济效益等各方面因素，最终选取大型坝占总比、串联率、库容均衡度、稳定系数、侵蚀模数、洪量模数及保收率7个指标建立布局评价指标体系，各指标释义及计算方法如下：

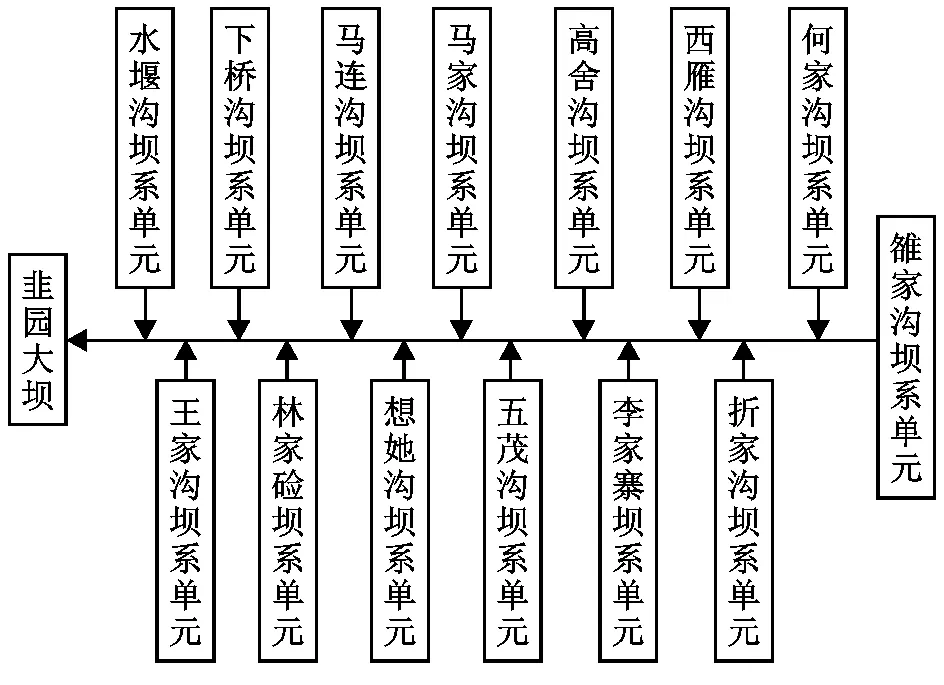
图1　韭园沟流域坝系框架控制关系结构图

(1)大型坝占总比。由于一个流域的防洪标准依赖于整个流域坝系，尤其是大型骨干坝的调蓄作用，因此大型坝库容占总库容的比值越大，其对洪水的调节能力就越强，流域对洪水的抵御能力也就越强。计算公式如下：

(1)

式中：L为大型坝占总比(%)；SL为流域坝系(单元)中大型坝总库容(万m3)；ST为坝系(单元)总库容(万m3)。

(2)串联率。由于在有限长度的流域沟道上，考虑溃坝风险，淤地坝的串联个数越多，单坝溃决后造成连锁溃坝的危险程度就越高，因此，串联率越低，布局相对越合理。计算公式如下：

(2)

式中：C为串联率(个/km)；Nc为淤地坝最大串联个数(个)；G为对应流域沟道长度(km)。

(3)库容均衡度。用来衡量流域坝系(单元)库容的均匀分配程度，该值越小，说明流域坝系(单元)对库容的分配越均匀。计算公式如下：

(3)

式中：B为库容均衡度(万m3/km2)；Smax，Smin分别为流域坝系(单元)内同类别淤地坝的最大库容与最小库容(万m3)；Ac为流域坝系(单元)控制面积(km2)。

(4)稳定系数。该值反映了坝系(单元)的相对稳定状态，同时也侧面影响流域的经济效益，而稳定性和经济性也是布局评价的重要内容。计算公式如下：

(4)

式中：D为稳定系数；Al，Ac分别为流域坝系(单元)的可淤地面积与坝控面积(km2)。

(5)侵蚀模数。单位时间、单位面积内被剥蚀并发生位移的土壤侵蚀量[t/(km2·a)]，是用来衡量土壤侵蚀程度的指标。坝系的建设，一方面可以拦截上游沟道产生的泥沙，另一方面在一定程度上改变了流域(沟道)的侵蚀形态，是布局合理性评判不可缺少的指标之一。本文利用韭园沟流域10 m分辨率的数字高程模型(DEM)以及2012年快鸟影像的土地利用解译图，基于ArcGIS平台，采用修正通用土壤流失方程(RUSLE)计算全区土壤侵蚀模数并进行强度分级(图2)，在流域划分的基础上进一步得出各坝系单元的平均侵蚀模数。

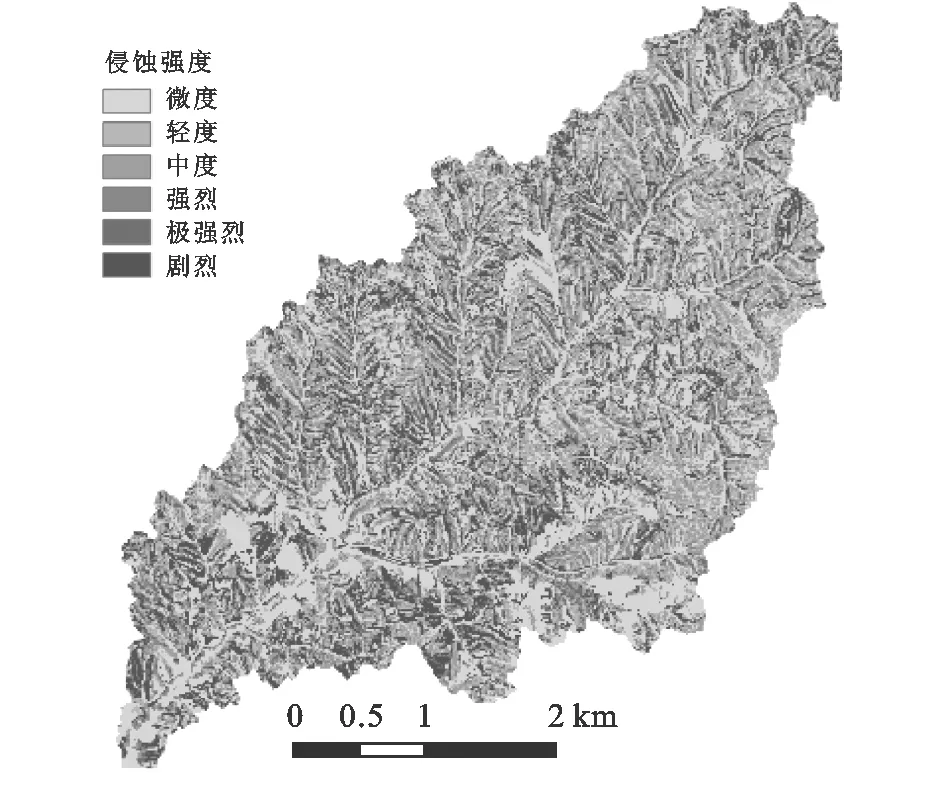
图2　韭园沟土壤侵蚀强度

(6)洪量模数。该指标用来衡量坝系(单元)拦蓄洪水的能力，计算公式如下：

(5)

式中：M为洪量模数(万m3/km2)；F选取300年一遇的洪水总量(万m3)；Ac为坝控面积(km2)；

(7)保收率：经不同重现期洪水以及淹水深度的计算，根据淹水深度不超过80 cm时坝地即可保收的标准计算保收率，该值也可影响到坝系(单元)的相对稳定和经济效益。计算公式如下：

(6)

式中：P为保收率(%)；N为淹水深度不超过80 cm时对应的重现期(a)。

1.2.3流域坝系布局合理性评价标准确定本文选用的7个指标中，除侵蚀模数、稳定系数和保收率有参考标准外，其余指标由于是新列指标，暂无统一标准，故结合数据属性和相关研究来拟定评价标准。其中关于稳定系数和保收率，研究表明多沙粗沙区坝地在20年一遇的洪水条件下，当作物保收率在80%以上时，其经济效益是相当可观的，可达到防洪保收的目的；当稳定系数达到1/30～1/50时，坝地属于初步利用阶段，为1/20～1/30时，坝地属于基本保收阶段，大于1/20时，该坝可实现相对稳定[7]；当大型占总比达到50%以上时，骨干坝可以对流域进行较好的控制，基本达到坝系建设的目标；串联率考虑当出现3座以上淤地坝串联时，坝系工程的安全风险增加。由此建立的坝系布局合理性评价标准见表1。

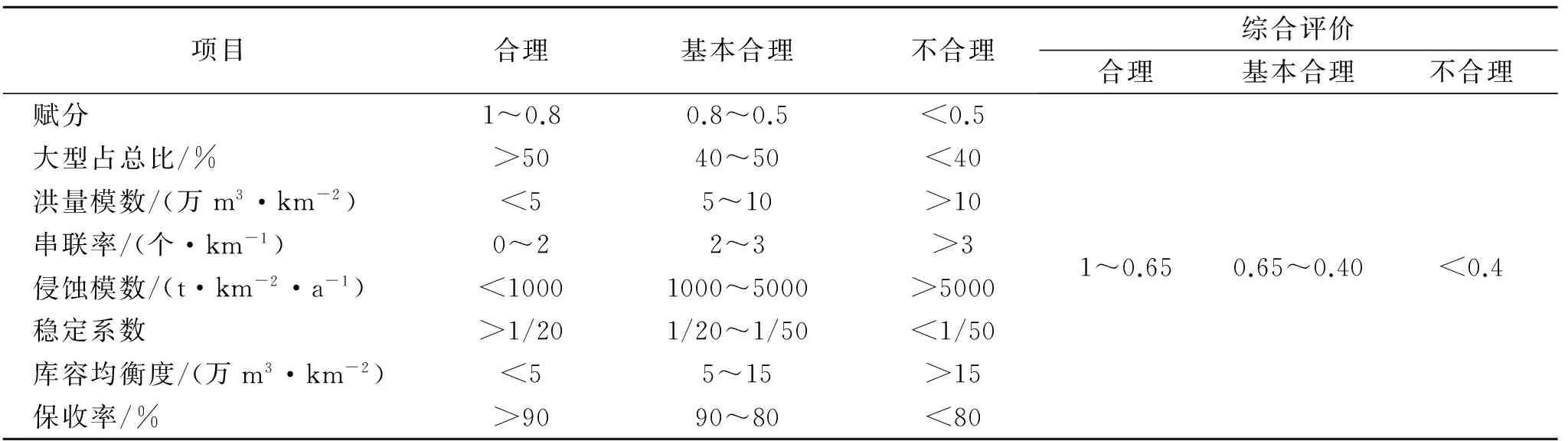
表1　流域坝系布局合理性评价标准

1.2.4指标权重的确定对于评价指标权重的赋值方法主要集中在层次分析法、德尔菲法等，其计算过程中均包含大量的主观因素影响，容易产生较大偏差。因此，为对比分析，本文除了采用层次分析法(AHP)外，还选取改进层次分析法(IAHP)、熵权法以及组合权重法分别进行权重计算。

(1)改进层次分析法。改进的层次分析法(IAHP)[8-10]确定权重向量克服了常规层次分析法中标度重要性以及权重计算和一致性检验的复杂性，具有直观、简捷的特点。其步骤如下：

① 构造判断矩阵。在同一层次中，对各评价因素的重要性进行两两比较，得到综合比较矩阵，并根据重要性程度排序指数构造对应的判断矩阵。各评价因素的重要性评判规则如下：

(7)

式中：kij是因素i和因素j的比较量化值。判断矩阵的计算公式为：

(8)

式中：cij为判断矩阵的对应元素；ri为重要性程度排序指数；m为矩阵的阶数；kij为比较矩阵的相应元素。

② 计算判断矩阵的优化矩阵。设原判断矩阵为C=[cij]mm，则优化矩阵的对应元素的计算公式为：

(9)

③ 计算评价指标权重值。计算各单一评价指标的权重值，并对其进行归一化处理，公式为：

(10)

式中：i，j=1，2，…，m；wi为第i个评价因素相应的归一化权重值；m为同一层次的评价指标个数。

(2)熵权法。为减少在确定权重过程中主观因素的影响，基于信息熵的群众赋值法实现了对数据本身信息有序性的客观反映，它通过评价指标值所构成的判断矩阵来确定指标权重，这样能在一定程度上消除由专家经验和主观打分带来的误差，使评价结果更符合实际[11]。其计算步骤[12]如下：

① 构建m个方案n个评价指标的判断矩阵：

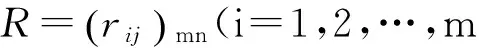
② 将判断矩阵进行归一化处理，得到归一化的判断矩阵B：

(11)

式中：rmax指同一指标下不同方案的最优指标值；rmin指同一指标下不同方案的最劣指标值。

③ 根据熵的定义，n个评价指标m个方案，由此确定评价指标的熵为：

(i=1，2，…，m；j=1，2，…，n)

(12)

为使lnfij有意义，假定：当fij=0时，fijlnfij=0；但当fij=1时，lnfij也等于零，显然不切合实际，并且有悖于熵的含义，故将fij修正为：

(13)

进而，第j个评价指标的熵权wj定义为：

(14)

(3)组合权重法。为合理地确定布局评价指标的权重，把指标的权重结构分为反映评价指标不同属性对布局合理性影响程度的主观权重和反映各评价指标样本值差异信息对布局合理性影响程度的客观权重，本文采用层次分析法(AHP)以及熵权法分别确定这些权重，然后利用最小相对信息熵原理将它们综合为组合权重，这样能够充分挖掘评价指标权重中的专家主观经验信息和各评价指标样本值的客观差异信息[13]。其中本次专家打分邀请10位专家参与，返回有效打分表9份。

综合指标的主观权重w1j与客观权重w2j，可获得对应的组合权重wj，j=1～m。显然wj与w1j和w2j都应尽可能接近，根据最小相对信息熵原理[14-15]有：

(15)

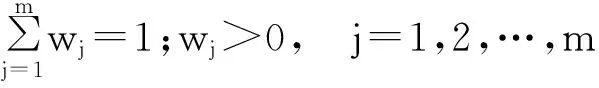
(16)

用拉格朗日乘子法解上述优化问题得：

(17)

2　结果与分析

2.1评价指标计算与赋值

在坝系单元划分的基础上，依次计算1个主沟坝系单元、14个子坝系单元以及全流域各指标值，汇总见表2。

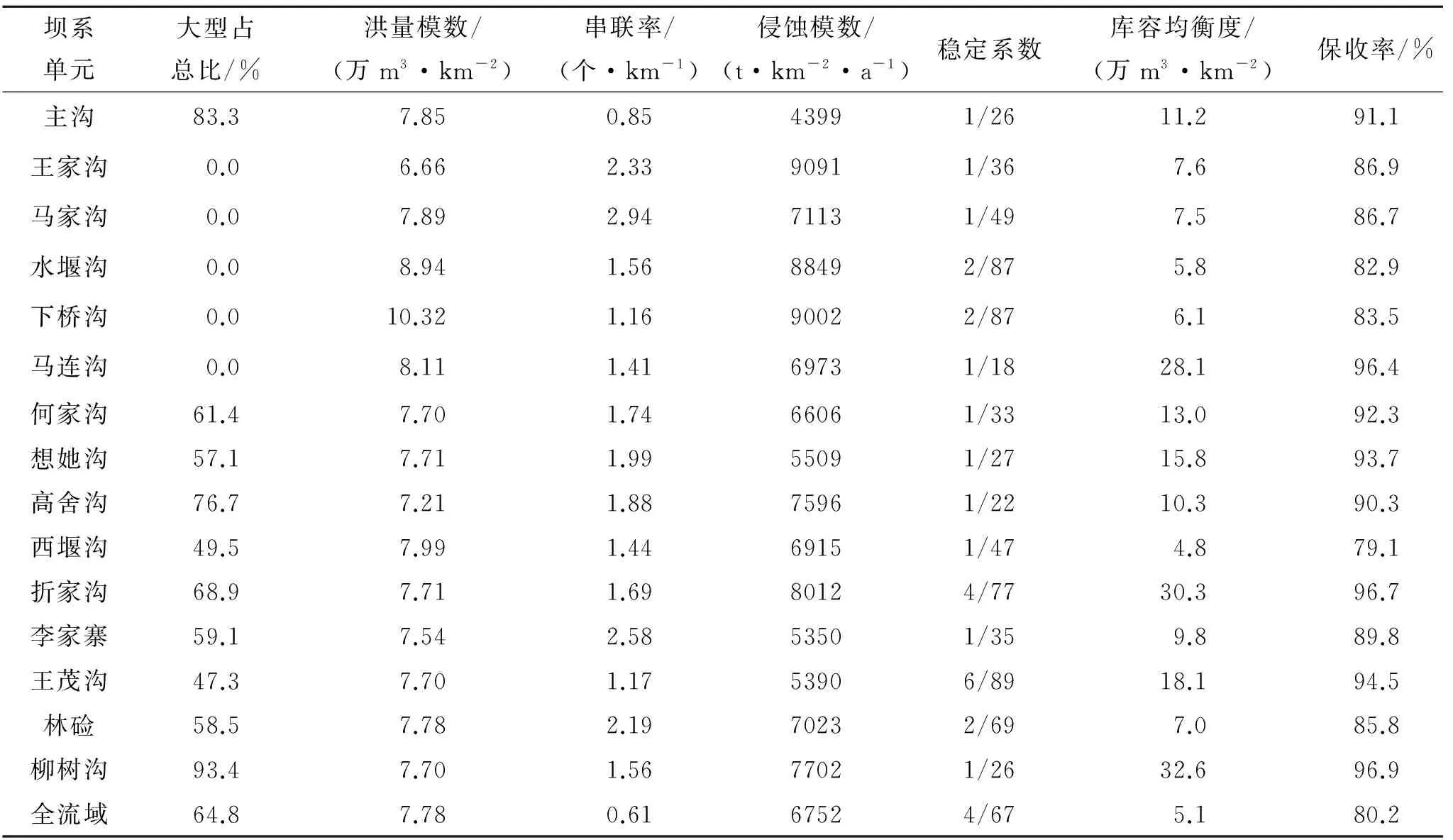
表2　韭园沟各坝系单元指标汇总

大型坝占总比根据其对洪水的调节能力进行定量赋值，当大型坝的库容控制率达到或超过50%时赋值为1，每减小10%，赋值相应减小0.2；洪量模数根据其对洪水的拦蓄能力进行定量赋值，当洪量模数小于5万m3/km2时赋值为1，每增加2万m3/km2，赋值相应减小0.2；串联率参考串联淤地坝连锁溃坝对下游工程的威胁程度进行定量赋值，当串联率为0时赋值为1，串联率每增加1，赋值减小0.2；侵蚀模数根据其对土壤侵蚀的控制程度进行定量赋值，当侵蚀模数小于4 000 t/(km2·a)时赋值为1，每增加2 000 t/(km2·a)，赋值相应减小0.2；稳定系数根据其对流域相对稳定的贡献率进行定量赋值，当稳定系数大于1/20时赋值为1，小于1/50时赋值为0，处于中间值时内插取值；库容均衡度根据其对库容的分配均匀程度进行定量赋值，当均衡度为0时赋值为1，每增加10万m3/km2，赋值相应减小0.1；保收率根据坝地保收标准进行定量赋值，当保收率小于80%时赋值为0，每增加5%，赋值相应增加0.2。各坝系单元指标标准化赋值汇总见表3。

2.2评价指标权重的计算

依次采用层次分析法(AHP)、改进层次分析法(IAHP)、熵权法和组合权重法分别计算各指标权重，汇总见表4。

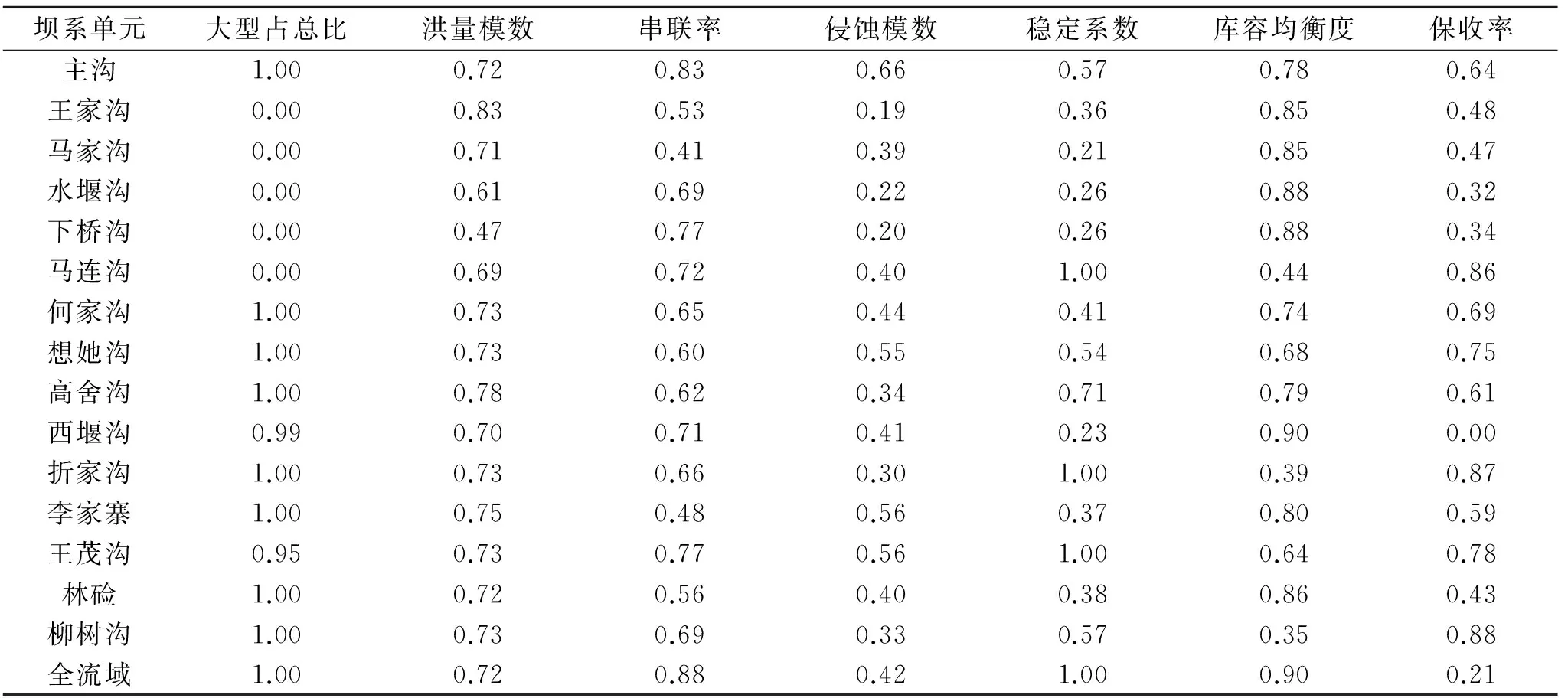
表3　坝系单元指标标准化赋值

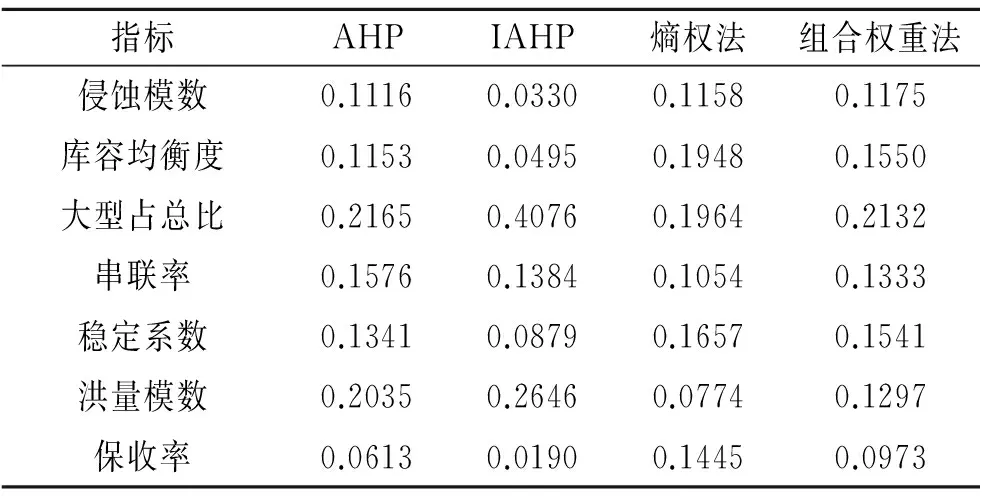
表4　不同方法的指标权重计算

2.3布局得分值计算与合理性评价

韭园沟流域坝系布局得分值计算如下：

(18)

式中：B为流域坝系单元布局综合得分；Ci为7个指标赋分值；Wi为对应指标的权重。

根据布局评价标准，不同方法所得布局得分值与合理性结果不同，汇总结果见表5。计算结果显示：韭园沟1个主沟坝系单元和14个子坝系单元布局多数是合理的，尽管个别坝系单元存在不合理布局，但从全流域来看，淤地坝坝系布局是合理的。相比坝系单元，由于整个流域的大型坝库容控制率较高，并且稳定系数较大，从而导致得分值较高。

表5　韭园沟流域坝系布局得分值与评价结果

由表5可知，各坝系单元中下桥沟坝系单元综合得分值较低，评价结果为不合理，从单项指标分值来看，是由于其在洪量模数、侵蚀模数、保收率3项指标的得分值较低，分析可能由于该坝系单元内单坝的设计标准偏低或放水建筑物的养护工作不到位，从而抵御洪水的能力不足所导致。结合韭园沟小流域2012年7月15日暴雨淤地坝水损调查情况得知，在该场暴雨中下桥沟流域的下桥沟2号坝的涵洞和卧管全毁，产生了较大的破坏，这在一定程度上验证了本结果的可靠性。

4种方法的评价结果中，除王家沟、马家沟、水堰沟和下桥沟存在差异以外，其余坝系单元合理性评价结果是一致的，这表明结果具有一定的可靠性。其中AHP法和熵权法评价结果完全相同，而IAHP法与组合权重法评价结果则趋于保守。分析表4可知，AHP法与熵权法权重差异主要在洪量模数和保收率上，前者主要通过专家打分进行确定，人为主观因素影响较大，而后者完全是基于数据本身计算而得，虽反映了各评价指标样本值的客观差异信息，但缺乏定性因素以及经验信息的考虑，故评价结果都各有缺陷。相对于AHP法，IAHP法由于在构造判断矩阵时对评价因素的重要性评判原则得到简化，主观性因素影响有一定程度的降低，因此各指标权重系数更能反映指标对布局合理性贡献率的大小及程度，由此得出的评价结果也更加合理。而组合权重法由于将反映评价指标不同属性对布局合理性影响程度的主观权重和反映各评价指标样本值差异信息对布局合理性影响程度的客观权重进行了组合计算，可充分挖掘评价指标权重中的专家主观经验信息和各评价指标样本值的客观差异信息，由此得出的结果更加合理、严谨和全面。因此，通过后两种方法计算得到的小流域坝系布局合理性取得了较理想的结果。

同时，综合分析表3与表5可看出，综合评价结果为基本合理或不合理的坝系单元对应大型占总比指标的分值均为0。分析表4，也可发现4种方法中大型占总比这一指标权重系数均达到最大，从而对其最终的布局得分值造成影响。这更加说明了大型骨干坝在坝系布局中的重要地位，加强骨干坝建设更应该在布局规划中得到重视。此外，结合综合评价结果与单项指标评价标准可知，当大型坝控制全流域50%以上，库容均衡度达到0～20万m3/km2，同时稳定系数达到1/25～1/20，洪量模数0～10万m3/km2，骨干坝串联个数低于2.5座/km时，此时的坝系布局基本上是合理的。

3　结 论

(1)韭园沟1个主沟坝系单元和14个子坝系单元布局多数是合理的，尽管坝系单元存在不合理布局，但从全流域来看，淤地坝坝系布局也是合理的；

(2)4种方法的评价结果除王家沟、马家沟、水堰沟和下桥沟存在差异以外，其余坝系单元合理性评价结果是一致的，这表明各结果具有一定的可靠性，各方法也具有一定的适应性，其中由于IAHP法和组合权重法在计算权重时的主观性得到了一定程度上的避免，评价结果更加严谨和合理，在小流域坝系布局合理性评价系统中具有广阔的应用前景；

(3)4种方法中大型占总比这一指标权重系数均达到最大，这更加说明了大型骨干坝在坝系布局中的重要地位，加强骨干坝建设更应该在布局规划中得到重视。由于本文所列指标均为新列指标，暂无统一标准，指标的相关性及适用性还有待进一步研究。

[1]王英顺,田安民.黄土高原地区淤地坝试点建设成就与经验[J].中国水土保持,2005(12):44-46.

[2]蔺明华,王志意,段文中.淤地坝研究的回顾与展望[J].中国水利,2003(9):62-64.

[3]陈骞.小流域坝系建设中的几个问题及建议[J].中国水土保持,2008(2):55-56.

[4]蒋耿民.淤地坝坝系工程总体布局综合评价指标体系及模型研究[D].陕西杨凌:西北农林科技大学,2010.

[5]蒋得江.试论小流域坝系总体布局合理性评价若干问题[J].河西学院学报,2009,25(5):48-52.

[6]田永宏.韭园沟示范区小流域坝系布局分析[J].中国水土保持,2006(9):21-22.

[7]田永宏,王英顺.黄河流域多沙粗沙区坝地防洪保收研究[J].中国水土保持,1997(4):18-22.

[8]蒋得江.黄土高原西部水土保持坝系布局与评价[M].郑州:郑州大学出版社,2010.

[9]陈风光,姚海林,史卫国.模糊综合评价法在堰塞湖风险评估中的应用[J].上海交通大学学报,2011(S1):67-70.

[10]Dyer J S.Remarks on the analytic hierarchy process[J].Management Science,1990,36(3):249-258.

[11]张先起,王臣博,李恩宽.小流域淤地坝坝系方案优选熵权属性识别模型[J].中国农村水利水电,2013(11):85-89.

[12]Chen S Z,Wang X J,Zhao X J,et al.An attribute recognition model based on entropy weight for evaluating the quality of groundwater sources[J].Journal of China University of Mining & Technology,2008,18(1):72-75.

[13]吴开亚,金菊良.区域生态安全评价的熵组合权重属性识别模型[J].地理科学,2008,28(6):754-758.

[14]Bierkens J,Kappen H J.Explicit solution of relative entropy weighted control[J].Systems & Control Letters,2014,72:36-43.

[15]雷功炎.关于将相对熵用于层次分析的简单注记[J].系统工程理论与实践,1995,15(3):65-68.

Evaluation of Overall Distribution of Check Dam System in the Jiuyuangou Watershed

WANG Dan,LI Zhanbin,LI Peng,GAO Haidong,ZHAO Binhua,YUAN Shuilong

(Key Laboratory of Northwest Water Resources and Environment Ecology of Ministry of Education,Xi′an University of Technology,Xi′an 710048,China)

The scientific layout of check dam system was related to the safety of flood control of a watershed.The evaluation of overall distribution of check dam system in the Jiuyuangou Watershed were carried out in order to provide theoretical basis for the planning,construction and design work of the dam system engineering of small watershed.The Jiuyuangou Watershed was divided into one main gully dam system unit and 14 sub dam system units,and then the evaluation system of overall distribution of check dam system was established by a comprehensive selection of 7 indexes including the proportion of key dams,series rate,capacity equilibrium degree,stability coefficient,erosion modulus,flood modulus and yield ensuring rate.The Analytic Hierarchy Process (AHP),Improved Analytic Hierarchy Process (IAHP),entropy method and combination weighting method were applied to calculate the weight of each index,through which the overall distribution of the check dam system of Jiuyuangou Watershed was evaluated.The results showed that: (1)although the distribution of part sub dam system units were unreasonable,that of the whole watershed seemed to be reasonable; (2)the results of the IAHP method and the combination weighting method were more reasonable because of their objective theory when calculating the weight coefficient; (3)the weight of the index ‘proportion of key dams’ reached the maximum in the four methods,which further indicated that key dam had a decisive influence on dam system layout; (4)when the key dams controlled above 50% of the whole watershed,capacity equilibrium degree reached to 0～200 000 m3/km2,stability coefficient 1/25～1/20,flood modulus 0～100 000 m3/km2,the number of series of key dam was less than 2.5 per kilometer,at this time,the overall distribution of check dam system was basically reasonable.

dam system unit; IAHP; entropy method; combination weighting; evaluation of distribution of check dam system

2015-09-12

2015-10-20

国家自然科学基金重点项目(41330858);国家自然科学基金(41471226，41401305)

王丹(1991—),女,陕西榆林人,在读硕士,研究方向为水文学及水资源。E-mail:danwang943@163.com

李占斌(1965—),男,河南镇平人,博士,研究员,主要从事土壤侵蚀和水土保持方面的研究。E-mail:zbli@ms.iswc.ac.cn

S157

A

1005-3409(2016)05-0049-07