当均匀带电体是什么形状时在带电体上某点有最大场强

姜付锦　吴 珊

(武汉市黄陂区第一中学　湖北 武汉　430300)



当均匀带电体是什么形状时在带电体上某点有最大场强

姜付锦吴 珊

(武汉市黄陂区第一中学湖北 武汉430300)

先用“对称性原理”对均匀带电体在表面某点产生最大电场强度时的形状进行了定性分析，然后用变分学的欧拉方程对物体的形状进行定量研究，最后对这个问题进行归纳和总结.

对称性原理欧拉方程泛函

一个均匀带电体的电荷量是一定的，若带电体是一均匀带电直线，则当直线弯成什么形状时在曲线上某一点产生的电场强度最大呢？若带电体是二维平面，则当带电平面是什么形状时在平面边缘某一点产生的电场强度最大呢？若带电体是三维立体结构，则当带电体表面是什么形状时在表面某一点产生的电场强度最大呢？它们会是圆形或球形吗？这其实是个泛函问题，本文先对物体形状作定性分析再对形状进行定量计算．

1　物体形状的定性讨论

如图1所示，以物体上某一点为原点O，竖直向上的方向为极轴，建立球坐标系(r,θ,φ)，其中r∈[0,∞),θ∈[0,π],φ∈[0,2π]，则物体上的任意一点可由坐标(r,θ,φ)确定，物体表面可由函数r=R(θ,φ)描述．要使原点处的电场强度最大，物体的形状应具有以下特性：

(2)物体形状具有旋转对称性，绕极轴旋转任意角度对称，故物体表面函数简化为r=R(θ)．由“对称性原理”[1]：原因中的对称性必反映在结果中，即结果中的对称性至少有原因中对称性那样多．

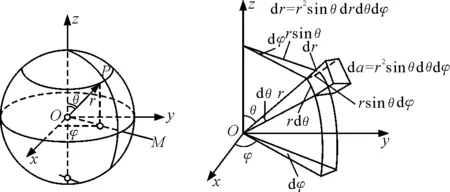
图1　物体形状的定性讨论

2　物体形状求解的一般方法

满足固定边界条件y(x0)=y0,y(x1)=y1的光滑函数集合中，求一个函数y=y(x)，满足条件(等周条件)

并使

2．1当带电体是三维物体时的形状[3]

设电荷连续分布的物体的电量为Q，电荷的体密度为ρ且保持不变，在球坐标系中物体的体积可以表示为

电场强度表达式为

由于物体具有旋转对称性，带电体在原点处产生的电场强度在垂直于极轴方向上的分量为零，物体在原点产生的电场强度为

令t=cosθ,R1(cosθ)=R(θ)，则

由上述的方法知

得

由等周条件得

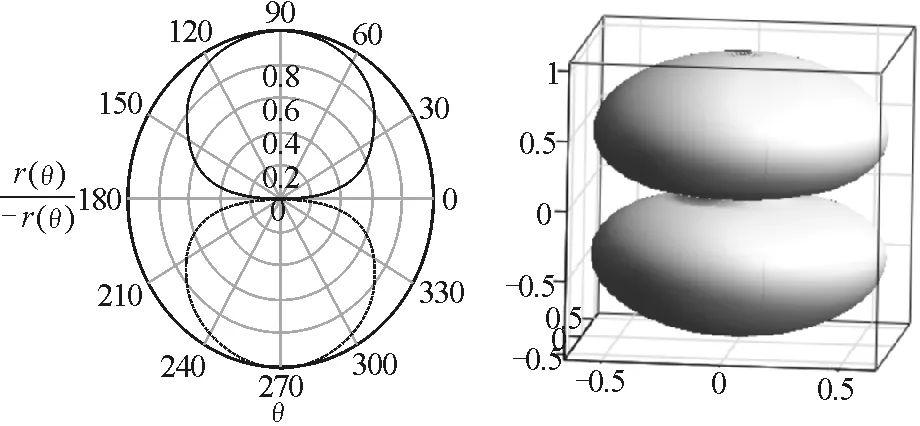
图2　带电体的三维结构图

2．2当带电物体是二维平面时的形状

设电荷连续分布的物体的电荷量为Q，面密度为σ且保持不变，在极坐标系中物体的面积可以表示为

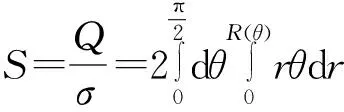
原点处的电场强度为

若令

t=cosθR1(cosθ)=R(θ)

则等周条件为

电场强度为

由上述的方法可知

得

即

由等周条件得

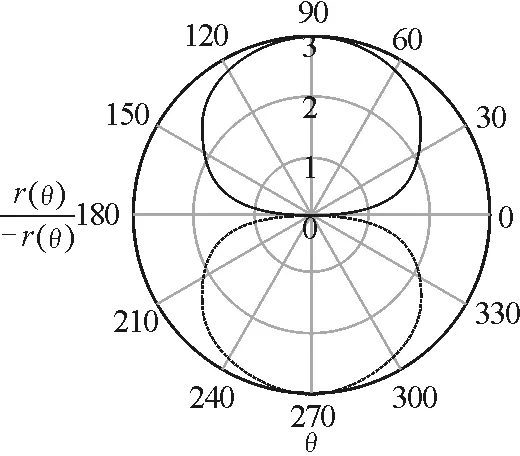
图3　带电体的二维平面的形状

2．3当带电体是一条粗细均匀曲线时的形状

设电荷连续分布的物体的电荷量为Q，线密度为λ且保持不变，物体的长度可以表示为

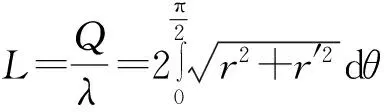
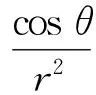
由等周条件得

图4　带电体是弯曲线时的形状

3　结语

通过对带电体的3种情况分析可以发现：

(1)物体的形状具有旋转对称性；

(2)物体上每个微元电荷在表面某一点产生的电场强度沿极轴方向上的分量相同；

(3)物体表面的形状可以表示为R(θ)=

1赵凯华.定性与半定量物理学．北京：高等教育出版社，1991.33

2欧斐君.变分法及期应用：物理、力学、工程中的经典建模．北京：高等教育出版社，2013.47～65

3杨星宇.力学中一个趣味问题的讨论．物理通报，2015(8)：57～59

4史友进，俞晓明.库仑摩擦最速降曲线问题的讨论．盐城工学院学报(自然科学版)，2012(6)

5史友进，俞晓明.库仑摩擦因数对串珠经典速降线与改进速降线下滑影响．牡丹江大学学报,2011(7)

2016-01-07)