新型无尾翼水下滑翔器升阻比性能的研究
2016-10-25吕鸿冠王天霖黄斯慧
吕鸿冠,黄 技*,王天霖,黄斯慧
(1.广东海洋大学 工程学院,广东 湛江 524088;2.大连海事大学,辽宁 大连 116026)
新型无尾翼水下滑翔器升阻比性能的研究
吕鸿冠1,黄技1*,王天霖2,黄斯慧1
(1.广东海洋大学工程学院,广东湛江524088;2.大连海事大学,辽宁大连116026)
采用标准k-ε两方程涡粘性模型,压力的隐式算子分割算法(PISO)求解时均Reynolds方程(RANS),对三种新型无尾翼水下滑翔器的升阻比性能进行研究。先对滑翔器摩擦阻力的CFD模拟结果与理论计算结果进行对比分析,验证CFD模拟结果的合理性与可靠性;再对不同迎流速度、不同速度攻角下的试验工况进行数值模拟,分析不同试验工况下滑翔器的粘压阻力与升力,得到不同试验工况下滑翔器的升阻比性能。研究结果表明,新型无尾翼水下滑翔器在5°~15°攻角区间内具有良好的升阻比,小攻角下圆碟型和飞碟型滑翔器的升阻比性能优于椭圆型滑翔器,而大攻角下椭圆型滑翔器相对其它两种具有更佳的升阻比性能,为新型无尾翼水下滑翔器升阻比性能的研究提供一定的思路。
水下滑翔器;无尾翼;升阻比;CFD
水下滑翔器是一种以浮标技术与水下机器人技术为基础,依靠自身浮力驱动的新型海洋工程装备。由于水下滑翔器与传统的浮标和水下机器人相比,具有操控性高、灵活性强、续航时间久、数据采集密度大等特点,以及其在海洋开发、军事勘察等领域的出色表现,水下滑翔器已逐渐发展为海洋工程装备领域的热门研究课题,受到很多工程师、科研人员等的高度关注。
目前,在整个世界范围内,欧美国家的水下滑翔器技术较为成熟。欧美国家的水下滑翔器以Slocum、Seaglide、Spray等为典型代表[1-4];21世纪初,日本东京大学TamakiUra实验室研发了ALBAC水下滑翔器[5],并在Sugura海湾进行试航;2005年,沈阳自动化研究所成功研发出中国第一台水下滑翔器“Sea-Wing”;2010年,国家海洋技术中心开始从事浅海型水下滑翔器“Sun-Glider”的研制,直到今天已经广泛应用于国内外海洋科学考察[6];2015年国家“863”计划项目资助的多家深海型水下滑翔器在南海进行了长航程集中海试比测,天津大学的深海型水下滑翔器“海燕”取得了最好的成绩,这标志着我国第一款达到实用化水平的深海型水下滑翔器工程样机的诞生。总的来看,国内的研究起步相对较晚,但也取得显著的进展[6-8]。
近年来,世界各国加大了海洋资源的开发力度,对海洋工程装备提出了更高的要求,传统的水下滑翔器已经难以满足实际的作业需求,一些学者总结了传统水下滑翔器的弊端,提出了新型水下滑翔器的一些新功能、新模块[6-8]。新型的水下滑翔器与传统的水下滑翔器相比,对整体外观设计、内部模块集成、实际作业表现及自身的水动力性能都有更高的要求。
哈尔滨工程大学王天、叶秀芬等[9]对圆碟形滑翔器的航姿控制进行研究,在碟形滑翔器水动力性能的基础上设计了控制系统算法;大连海事徐宏翔、王天霖等[10]对碟形浮标进行CFD数值计算,得到碟形浮标的水动力性能,上海交通大学张怀新、潘雨村等[11]对圆碟形滑翔器的阻力性能进行研究,得到碟形滑翔器的阻力规律。本文结合流体理论和CFD求解技术,对椭圆型(Ellipse)、圆碟型(Roundel)、飞碟型(Disk)三种新型无尾翼水下滑翔器进行分析,对滑翔器的阻力、升力及不同工况下的升阻比性能进行研究。
1 数值求解控制方程
笛卡尔坐标系下,水下滑翔器周围的粘性不可压缩三维流场的Navier-Stokes方程为:
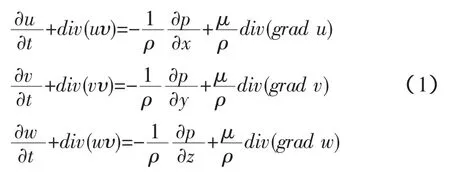
考虑滑翔器周围流场湍流脉动的影响,对式(1)采用时均法,将湍流运动看成两个流动叠加而成,一部分为时均流动,一部分为瞬时脉动流动。则Reynolds时均Navier-Stokes方程(RANS)定义为:

上述的RANS方程中引入了湍流脉动值的Reynolds应力项,需采用湍流模式对其进行封闭求解。这里采用标准k-ε两方程涡粘性模型封闭RANS方程,算法采用求解瞬态迭代的PISO算法。
2 滑翔器选型及工况设计
滑翔器的选型一共三种:椭圆型(Ellipse)、圆碟型(Roundel)、飞碟型(Disk),如图1所示:

图1 Ellipse、Roundel、Disk滑翔器的三维模型
定义工况代号“DA0V0.1”,其中首项为滑翔器类型:D(Disk)、E(Ellipse)、R(Roundel);第二项A(Angle)为攻角值;第三项V(Velocity)为速度值,如“DA0V0.1”代表飞碟形水下滑翔器0°攻角0.1 m/s迎流速度。则试验工况如表1~表2所示:

表1 试验工况表-不同迎流速度
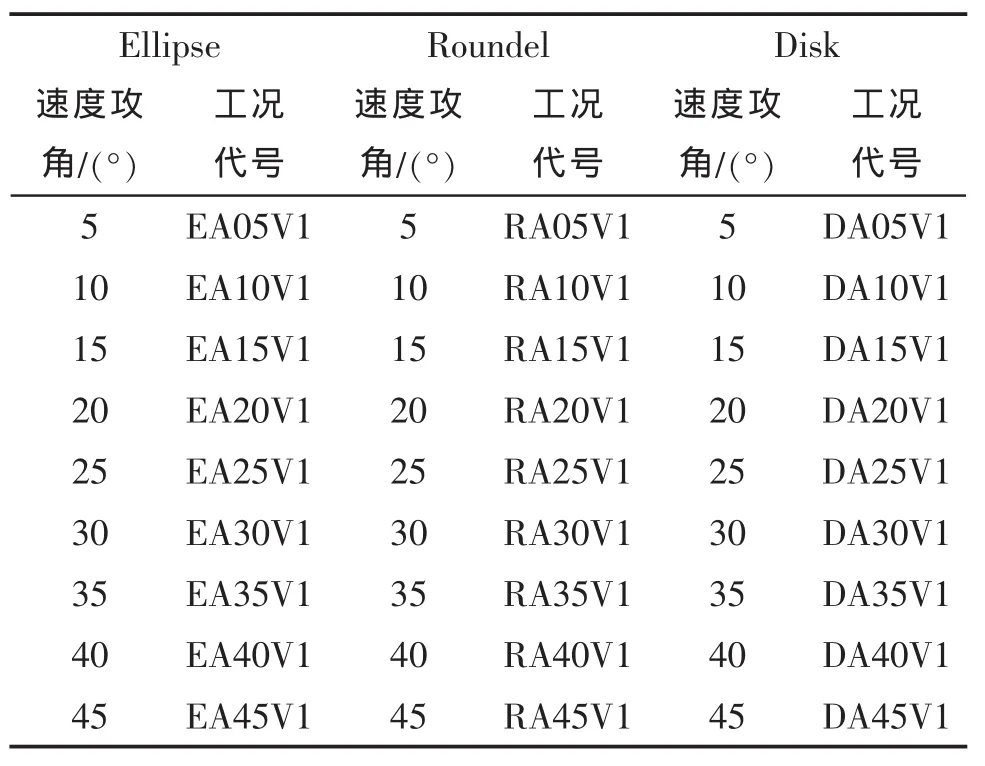
表2 试验工况表-不同速度攻角
3 滑翔器摩擦阻力的讨论
3.1滑翔器的阻力构成
水中运动物体受到到的总阻力Rt由摩擦阻力Rf、粘压阻力Rpv和兴波阻力Rw组成,即:

对于大部分水中运动的物体,如水下机器人、水下滑翔器等,兴波阻力Rw可忽略不计,则滑翔器运动时,受到的总阻力为:

由于水下运动物体的外型相对复杂,摩擦阻力Rf和粘压阻力Rpv目前尚无成熟的理论体系直接求解。对于摩擦阻力Rf,目前大部分运用“相当平板假设”进行计算;而对于粘压阻力,目前尚无理论进行计算,而是通过水池试验或CFD技术进行研究。
3.2摩擦阻力系数
水中运动物体受到的摩擦阻力为:

式中:Cf为摩擦阻力系数;ρ为流体密度;v为迎流速度;S为湿表面积。
对于摩擦阻力系数Cf,目前主流的计算公式主要有边界层速度指数型分布公式、Schoenherr公式、Prandtl-Schlichting公式、Hughes公式、1957ITTC公式。
(1)边界层速度指数型分布公式
假设边界层内的速度分布形式为指数分布,经过试验结果修正后的指数分布公式为:

(2)Schoenherr公式
1932年Schoenherr运用边界层速度为对数分布的假设,并依据平板拖曳试验的数据,给出下列的摩擦阻力系数表达式:

上述公式为Schoenherr公式,1947年美国船模试验池会议(ATTC)决定以该式作为摩擦阻力的标准公式,故此公式又称为1947ATTC公式。
(3)Prandtl-Schlichting公式
Prandtl、Schlichting等人运用与1947ATTC公式相同的原则,得到与式(7)十分相似的Prandtl-Schlichting公式,该公式的表达式为:

(4)Hughes公式
1952年Hughes根据以往的平板试验数据,提出平板摩擦阻力系数与展弦比有关的理论,给出以下公式:

(5)1957ITTC公式
1957年在西班牙马德里召开的第八届国际船模试验池会议(ITTC)上根据几何相似模型阻力试验结果,认为Schoenherr公式、Prandtl-Schlichting公式等传统的摩擦阻力计算公式在低雷诺数时偏低,于是提出了新的公式,叫做“1957年国际船模试验池实船-船模换算公式”,简称1957ITTC公式:

式(7)~式(8),式(10)为当前最常用的公式,式(7)在美国的应用最为普遍,式(8)在欧洲大陆的应用最为普遍。我国目前采用1957ITTC公式[12]。
4 数值模拟分析
4.1滑翔器的摩擦阻力
通过对比相同攻角、不同迎流速度下三种选型的CFD模拟结果与理论计算结果,验证CFD模拟结果的合理性与可靠性。采用六面体结构网格占优法建立三种滑翔器的网格模型,在边界壁面处(Wall)处采用非结构网格,流场区域采用结构网格;在迎流区域加密网格以捕捉滑翔器周围流场的变化;滑翔器壁面划分三棱柱边界层网格,以精确捕捉滑翔器的升力、阻力信息。网格划分信息如表3所示,边界条件如图2所示,核心区域网格如图3所示。
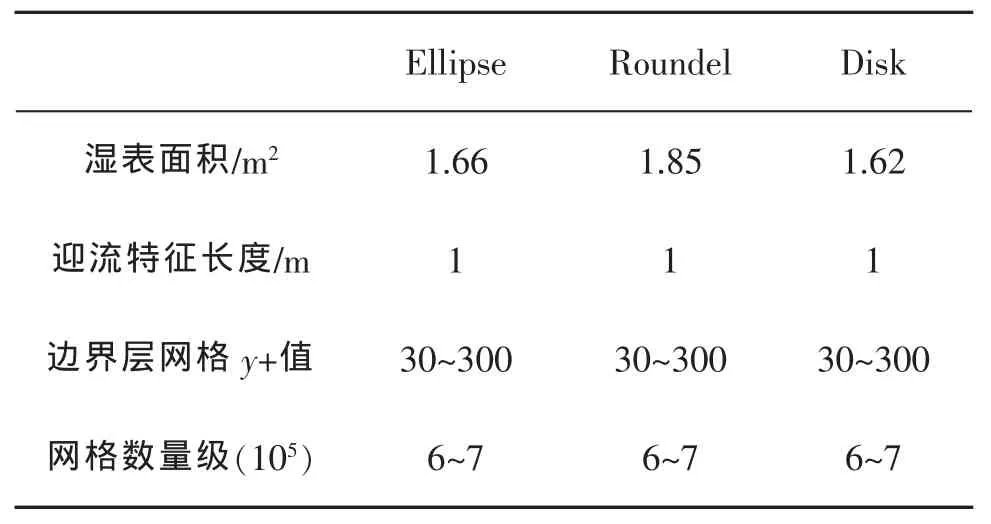
表3 网格信息

图2 边界条件设置

图3 核心区域的结构网格
在标准k-ε两方程涡粘性模型中使用标准壁面函数,以初始y+值为50作为基准,通过理论计算控制第一层边界层网格厚度于0.005 m左右。每种计算工况均划分5层边界层网格,通过不断调整第一层边界层网格高度控制y+值在30~300之间,以保证第一层网格节点在粘性层流子层之上。如果第一层边界层网格高度过小,即y+值低于30,则会导致第一层网格节点落入粘性子层,得到不准确的升力、阻力数据。一般来说,对于通常的湍流计算,y+在30~60之间可保证计算精度。

表4 不同经验公式下的摩擦阻力系数

图4 滑翔器理论摩擦阻力计算结果对比
从图4第一张数据图可看出,不同经验公式计算的摩擦阻力系数基本差别不大。而Hughes公式相对其它公式偏小,这是因为Hughes公式是根据有限展弦比(三因次流动)平板数据外插得到的。总体来看,经验公式的计算值基本分布在一个常数周围。从图4第二张到第四张数据图还可看出,利用经验公式计算滑翔器得到的摩擦阻力十分接近,阻力曲线基本呈现水平分布。

表5 滑翔器摩擦阻力的理论计算值

表6 滑翔器摩擦阻力的CFD模拟结果
从图5可看出,滑翔器的摩擦阻力随着迎流速度的增加而增加,且阻力变化趋势近似抛物型,与摩擦阻力的计算公式(二次型)吻合得很好。对比图5各条摩擦阻力曲线还可发现,CFD模拟结果与理论计算结果相当接近,每种外型的CFD摩擦阻力曲线与五条理论摩擦阻力曲线基本吻合,证明了每种工况的网格划分方式、边界层网格厚度定义,及各种求解参数设置的正确性。在此基础上,可进一步讨论滑翔器的在不同速度攻角下的升阻比性能。

图5 理论计算结果与CFD模拟结果的对比
4.2滑翔器的粘压阻力
粘压阻力一直是流体力学中的难题,由于水下运动物体形状的复杂性,目前尚无成熟的理论体系对其进行定量计算。但是,对粘压阻力的定性分析,目前有较为成熟的理论体系。水下运动物体的粘压阻力主要取决于物体的形状及流体的流态,还与边界层的流动情况有着密切的关系。新型滑翔器的三种不同选型在外观上有着巨大的差别,故新型滑翔器的粘压阻力是重要的水动力性能参数。

图6 边界层分离现象[13]
根据边界层理论可知,当滑翔器在迎流方向的下游处满足一定的条件时会出现粘性漩涡,导致滑翔器的粘压阻力急剧增大。将滑翔器表面某一局部区域放大,如图6所示。设边界层外流体微团的速度在3时达到最大值Umax,压力达到最小值Pmin。现在基于能量观点,将滑翔器的绕流运动划为3个过程分析滑翔器的粘压阻力。
第一个过程:则从1到3区间内,滑翔器边界层外部的流体微团速度呈递增趋势,呈压力递减趋势,此区域为顺压梯度区。当流体微团到达3时,压能全部转化为动能,此时速度达到最大值Umax,压力达到最小值Pmin。
第二个过程:超过3点后,压力沿着流动方向呈递增趋势,流体微团开始进入逆压梯度区。从力学理论分析可知,在顺压梯度区时,流体微团虽然受到粘性剪应力的作用,但是在正压梯度下,流体微团仍拥有足够的动能顺利前进,在3处达到最大速度Umax。当流体微团经过3后,进入了逆压梯度区,此时流体微团的动能不仅要转化为压能,而且还要提供一部分能量克服粘性阻力做功,在这双重阻碍下,流体微团的动能不断降低。
第三个过程:当流体到达S点的时候,动能被完全消耗,速度降为0,此时在逆压梯度的作用下,流体微团开始回流。从流体理论可知,滑翔器边界层外的流体与来流速度相同,而边界层内的速度与来流速度相反,故在尾部处出现回流,产生了粘性漩涡。这部分漩涡的维持需要不断消耗能量,导致滑翔器表面边界层分离点下游的压力无法继续升高,保持着和分离点一样的压力值。经过上述分析可知,滑翔器的前后存在一个压力差,滑翔器运动的时候需要克服这个压力差做功,必须消耗额外的能量,这便是是滑翔器粘压阻力的由来。
实际上,绕流过程不一定会产生边界层分离现象。如果将物体设计成流线型,可大大降低边界层分离的几率。另外,边界层是否分离还与速度攻角有着非常大的联系,即使是流线型物体,在小攻角情况下无分离,但是在大攻角的情况下便可能会发生分离。
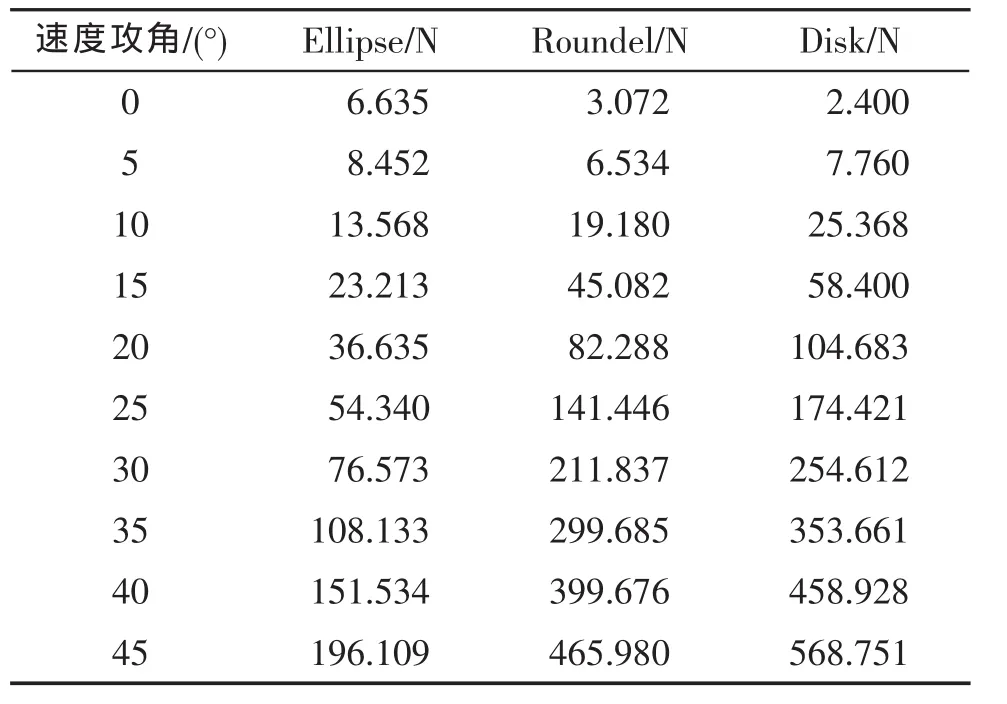
表7 不同速度攻角下滑翔器的粘压阻力

图7 不同速度攻角下滑翔器粘压阻力的变化趋势
从图7可明显看出,Disk滑翔器的粘压阻力随着迎流速度的增大而急剧增大,而Ellipse滑翔器的变化则十分缓和。尤其当速度攻角为45°时,Disk滑翔器的粘压阻力为Ellipse滑翔器的5倍。根据上述的分析结果可推测,造成这种现象的根本原因在于Disk滑翔器与Ellipse滑翔器外观的巨大差异,导致两者的粘压阻力出现极大的差别。Disk滑翔器对速度攻角的变化十分敏感,即随着速度攻角的变化,边界层分离现象会明显加剧,迎流后方出现强漩涡区,导致粘压阻力的急剧增大。而Ellipse滑翔器对速度攻角变化的反应相对缓和,边界层分离现象不明显甚至不出现边界层分离现象。
下面根据流场的分布情况来验证推论的准确性。15°,25°,35°,45°速度攻角的工况下,Disk滑翔器和Ellipse滑翔器周围的流场分布如图8~图9所示:

图8 15°,25°,35°,45°速度攻角下Disk滑翔器周围流场的分布情况

图9 15°,25°,35°,45°速度攻角下Ellipse滑翔器周围流场的分布情况
从图8~图9可看出,Disk滑翔器对速度攻角的变化非常敏感。当速度攻角为15°时,边界层分离现象不明显,而当速度攻角增加到25°时,迎流方向的后背处开始出现漩涡,从图7可得知此时粘压阻力会大幅度增加,接近翻倍;而Ellipse滑翔器的粘压阻力增加非常小,几乎不变。当速度攻角达到45°时,Disk滑翔器在迎流方向的后背处出现强漩涡,此时粘压阻力急剧加大,而Ellipse滑翔器粘压阻力增加值相对较小,边界层分离现象不明显甚至不出现边界层分离。造成这种现象的根本原因是Ellipse滑翔器更符合流线型外观设计,Ellipse滑翔器贴体流场变化相对缓和,不会出现巨幅震荡,故大攻角时Ellipse滑翔器更具有实际的应用价值。
4.3滑翔器的升阻比
滑翔器的升阻比如表8~表10、图10所示。

表8 不同速度攻角下Ellipse滑翔器的升阻比

表9 不同速度攻角下Roundel滑翔器的升阻比

表10 不同速度攻角下Disk滑翔器的升阻比

图10 滑翔器在不同速度攻角下的升阻比性能
从图10可看出,无论哪种选型的滑翔器,升阻比均呈现先升高后降低的趋势。在5°~15°速度攻角范围内,滑翔器的升阻比达到最大值。在小攻角情况下,Disk滑翔器和Roundel滑翔器相对Ellipse滑翔器具有更优的升阻比性能;而在大攻角情况下,Ellipse滑翔器以其优良的流线型外观在升阻比性能方面表现出巨大的优势。
5 总结
利用流体理论与CFD求解技术对三种新型无尾翼水下滑翔器的升阻比性能进行研究,得到了滑翔器重要的升阻比性能参数。滑翔器在速度攻角为5°~15°的范围内具有良好的升阻比性能。在小攻角情况下,Roundel滑翔器和Disk滑翔器的升阻比性能表现优于Ellipse滑翔器;而在大攻角情况下,Ellipse滑翔器的升阻比性能相对Roundel滑翔器和Disk滑翔器更具实际应用价值。
[1]SStommel.The SlocumMission[J].Oceanography,1989,2(1):22-25.
[2]Douglas C Webb,Paul J Simoneai,Clayton P Jones.SLOCUM:An Underwater Glider Propelled by Environmental Energy[J].IEEE Journal ofOceanic Engineering,2001,26(4):447-452.
[3]Eriksen C C,Osse T J,Light R D,et al.Seaglider:A Long-Range Autonomous Underwater Vehicle for Oceanographic Research[J].IEEE Journal ofOceanic Engineering,2001,26(4):424-436.
[4]JeffS,Russ E D,Owens W B,et al.The Autonomous Underwater Glider"Spray"[J].IEEE Journal of Oceanic Engineering,2001,26(4):437-446.
[5]Tomoda Y,Kawaguchi K,Ura T,et al.Development and Sea Trials of a Shuttle Type AUV ALBAC[C]//8th Int.Symposium on Unmanned Untethered Submersible Tech,1993:7-13.
[6]温浩然,魏纳新,刘飞.水下滑翔机的研究现状与面临的挑战[J].船舶工程,2015,01:1-6.
[7]李志伟,崔维成.水下滑翔机水动力外形研究综述[J].船舶力学,2012,07:829-837.
[8]李杰,周兴华,唐秋华,等.水下滑翔机器人研究进展及应用[J].海洋测绘,2012,01:80-82.
[9]王天.新型碟形水下机器人及其航姿预测控制系统研究[D].哈尔滨:哈尔滨工程大学,2013.
[10]徐宏翔.基于CFD模拟方法的圆碟型浮标水动力分析[D].大连:大连海事大学,2014.
[11]张怀新,潘雨村.圆碟形潜水器阻力性能研究[J].上海:上海交通大学学报,2006,06:978-982+987.
[12]盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2003.
[13]王家楣,张志宏,马乾初.流体力学[M].大连:大连海事大学出版社,2010.
[14]孟凡豪,严天宏,何波,等.水下滑翔器整体外形设计及水动力性能分析[J].海洋工程,2014,02:61-71.
Research on a New Type of Tailless Underwater Glider
LV Hong-guan1,HUANG Ji1,WANG Tian-lin2,HUANG Si-hui1
1.College of Engineering,Guangdong Ocean University,Zhanjiang 524088,Guangdong Province,China;
2.Dalian Maritime University,Dalian 116026,Liaoning Province,China
This paper uses the standard κ-ε two equation eddy viscosity model and the pressure implicit with splitting of operators(PISO)algorithm to solve the Reynolds-Averaged Navier-Stokes(RANS)equation for studying three new types of tailless underwater gliders in their lift-drag ratio performances.The CFD simulation results are compared with the results of theoretical calculation of the friction of the glider for verifying the rationality and reliability of the CFD simulation results.Then numerical simulation is conducted for the experimental states under different approach speeds and different speeds of attack angle,in order to analyze the viscous-pressure resistance and elevating force,obtaining the lift-drag ratio performances of gliders under different experimental states.The research results show that the new type of tailless underwater glider has a good performance in lift-drag ratio between the 5 to 15 degree attack angle.It is showed that the lift-drag ratio of the Roundel or Disk glider is higher than that of Ellipse glider under small attack angle,while the Ellipse glider has a higher lift-drag ratio than others under large attack angle.The study results provide some ideas for the research of new-type tailless underwater gliders.
underwater glider;tailless;lift-drag ratio;CFD
U661.31;P715.5
A
1003-2029(2016)04-0011-09
10.3969/j.issn.1003-2029.2016.04.003
2015-11-26
广东省青年创新人才类项目资助(2014KQNCX086,2014KQNCX081);广东省大学生科技创新培育专项资助项目(pdjh2016a0226)
吕鸿冠(1994-),男,主要研究方向为船舶与海洋工程。E-mail:lhggzyx2015@163.com
黄技(1988-),男,硕士,讲师,主要研究方向为船舶与海洋结构设计。E-mail:dmuhuangji@163.com
