考虑减速机背隙的3-RRR并联机构的运动学标定*

张宪民　曾磊

(华南理工大学 广东省精密装备与制造技术重点实验室，广东 广州 510640)



考虑减速机背隙的3-RRR并联机构的运动学标定*

张宪民曾磊

(华南理工大学 广东省精密装备与制造技术重点实验室，广东 广州 510640)

为了提高宏动并联平台的定位精度，推导了考虑减速机背隙的3-RRR并联机构误差模型,同时建立不考虑减速机背隙的误差模型用于对比，以验证该模型的有效性；通过实验测量末端平台位姿误差并分别辨识两个误差模型参数，根据距离反比法进行空间插值实现误差补偿并完成运动学标定.根据标定结果修正逆运动学模型，通过测量末端平台位姿误差分布可知，文中提出的考虑减速机背隙的误差模型优于不考虑减速机背隙的误差模型.文中提出的考虑减速机背隙的运动学标定提高了并联机构的定位精度，为该类并联机构用于高精密宏微结合提供了基础.

并联平台；减速机背隙；运动学标定；距离反比法；位姿误差；定位精度

并联机构由于对称的构型，对热膨胀和关节间隙的影响有相互补偿的作用，又由于闭环运动链的存在，使得各个支链间相互作用，从而能实现较高精度的定位[1].然而实际中由于加工误差、装配误差以及杆件的变形等因素，使得实际系统异于理论模型，从而降低了并联机构的定位精度[2].

目前主要是利用运动学标定来提高并联机构的定位精度[3-5].运动学标定主要分为4个步骤：系统误差建模、误差测量、参数辨识和误差补偿[5].目前，在系统误差建模方面已有大量研究，其中误差源大致可以分为两类：几何参数误差(如杆件的长度，安装角度误差等)以及非几何参数误差(如齿轮间隙、关节间隙等)[7].一些文献中假设非几何参数误差的影响较小，仅考虑了几何误差参数，最终标定出来的结果不够理想.实际上非几何参数误差的存在会影响机构的定位精度，因此在高精密场合，非几何参数误差不能够忽略.

邵珠峰等[8]在保持柔性并联机构基本不变的前提下，利用线尺实现机构的自标定，精度仅达到0.5 mm，其未考虑驱动端的误差以及关节间隙；马立等[9]采用外部标定法利用BP神经网络补偿并联机器人定位误差，精度达到了80 μm，其未考虑理论结构参数的误差；Judd等[10]概述了机器人的非几何参数误差源，包括齿轮间隙误差、伺服误差、结构变形误差以及齿轮磨损误差等；Slamani 等[11]建立了关于ABB串联机器人含关节间隙的误差模型并通过实验识别了关节间隙的大小；张宪民等[12]通过建立含关节间隙的误差模型，完成了3-RRR并联机器人的运动学标定，精度达到了±30 μm，但是标定过程复杂繁琐，不适合实际运用.

目前尚未发现有文献在并联机构的误差建模时考虑驱动端减速机的背隙.文中针对平面3-RRR并联机器人推导了考虑减速机背隙的运动学标定以及不考虑减速机背隙的运动学标定；使用激光跟踪仪测量平面3-RRR并联机器人末端动平台的位姿误差，然后利用最小二乘法分别辨识两误差模型的参数，并根据相应的辨识结果修正逆运动学模型；最后对比了考虑减速机背隙和不考虑减速机背隙的运动学标定后平面3-RRR并联机器人末端动平台的位姿误差分布.

1　考虑减速机背隙的误差建模

如图1所示，平面3-RRR并联机器人由静平台、动平台和3组连杆组成.其通过伺服电机带动与之相连的减速机使得驱动杆旋转，经过从动杆传递到动平台，使得末端平台实现3个自由度运动.

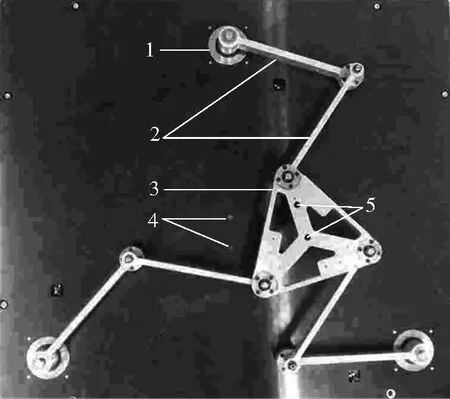
图1平面3-RRR并联机器人

Fig.13-RRR planar parallel robot

1—伺服电机以及减速机；2—连杆；3—动平台；4—基准孔；5—定位孔

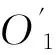
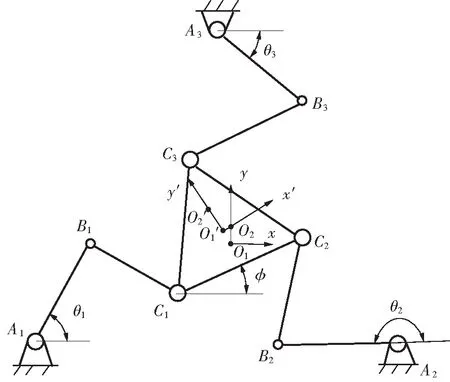
图23-RRR并联机器人结构示意图

Fig.2The structural representation of 3-RRR parallel robot

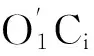
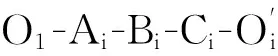
r=di+Rθiaie1+bini-Rφhi

(1)

其中，i=1，2，3.

两边微分整理得：

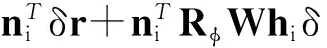
(2)

其中:

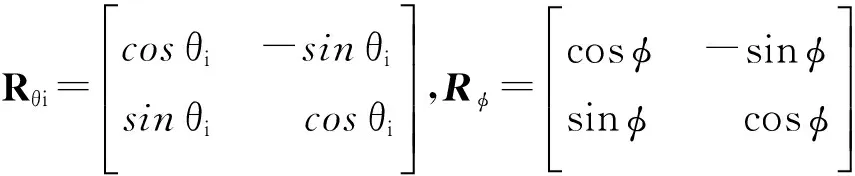
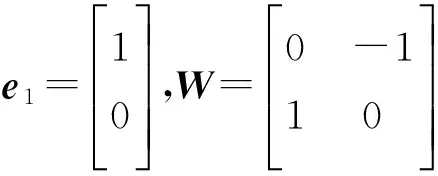
文中3-RRR并联机器人的理论结构参数如下：静平台坐标系中驱动关节Ai距原点距离400mm，间隔120°对称分布；驱动杆名义杆长245mm；从动杆名义杆长242mm；动平台坐标系中关节Ci距动平台原点112mm，间隔120°对称分布.

其中Bi以及Ci处(i=1，2，3)使用的是NSK高精密双列角接触球轴承，轴与轴承内圈以及座孔与轴承外圈均是采用过盈配合，并且使用了轴套与端盖进行预紧，故此6处的轴承间隙不明显；每根杆件的刚度都是足够大的，杆件变形不予考虑.并联机器人具有高负载以及响应速度快等优点，这需要选择转动惯量小的伺服电机.该种电机的额定转矩较小，为了实现高负载需使用减速机提高输出转矩；文中使用了减速比为1∶10，背隙等级为P0(不大于3弧分)的利茗行星减速机.该减速机有两个缺点：一是内部齿轮的刚度不够；二是微调整时由于回程间隙的存在会产生角度误差.减速机背隙指的是将输入端固定，输出端顺时针和逆时针方向旋转，使输入端产生±2%的额定扭矩时，减速机输出端输出一个微小的角位移[14].单位“弧分”即1°的1/60.3-RRR并联机器人进行点到点定位或者轨迹跟踪的时候，驱动端输出时时刻刻均在伺服驱动器的作用下微调整，故有必要考虑减速机背隙对定位精度的影响.

3-RRR并联机器人每次运动前，末端平台均需要在激光跟踪仪的引导下回到原点0°位姿，由于误差源使驱动杆的位置与理论位置不同，存在驱动电机转角误差δγi(初始电机转角偏差)，并在整个测量过程中保持不变.现假设减速机背隙引起的角度误差为δηi，因此δθi可表示为

δθi=δγi+δηi

(3)

其中，i=1，2，3.

新的误差模型变为

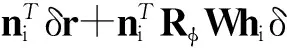
(4)

通过式(4)可以发现产生终端误差的源头有18项，分别是驱动端位置误差、驱动杆长度误差、减速机背隙引起的误差、初始电机转角偏差、从动杆长度误差以及动平台加工误差.通过测量其工作空间内多个点的末端姿态误差以及初始电机转角偏差，然后利用最小二乘法辨识出全部的误差项δdxi、δdyi、δai、δηi、δbi、δhxi、δhyi[15].

2　误差补偿

根据末端平台在工作空间内有限个点的位置误差，利用相关的插值方法预测其在整个工作空间的误差分布，然后将相应的误差补偿到关节空间便完成了误差补偿[16].

文中采用距离反比法进行空间插值，即每个采样对插值结果的影响随着距离的增加而减弱，故赋予距目标点近的样本点的权重较大[17].该算法具体如下.

已知样本点为(xj，yj)，j=1，2…，m；设工作空间内一点(x0，y0).若该点是样本点，则其误差值取其对应的误差矢量；如果不是样本点，则有：

(5)

其中：vj为样本点(xj，yj)处的误差矢量；wj为样本点(xj，yj)所占的权重；dj为样本点(xj，yj)到插值点(x0，y0)的距离.

综上，将末端平台的姿态误差补偿到关节空间的流程为：①根据期望位置利用上述插值方法预测出实际位置；②求解从实际位置到期望位置关节空间的变化量；③末端平台运动完后通过上位机输入需要补偿的关节角度完成误差补偿.

3　3-RRR并联机器人标定实验

本次实验中，3-RRR并联机器人是由安川伺服电机外接利茗行星减速机进行驱动，并通过美国GALIL公司开发的DMC-1886PCI总线运动控制卡进行控制.安川电机拥有24位增量式编码器，位置控制模式下每个脉冲旋转0.000 03°，使末端平台可以在x和y方向上平移1μm，为实现3-RRR并联机器人的微定位调整提供了基础.使用的测量工具是德国徕卡公司生产的LeicaAT901-B型激光跟踪仪，其分辨率为0.1μm，测量精度为10μm.

实验的具体过程如下：

(1)工作空间内布点：在120mm×120mm的工作空间内，采用方形布点的方式，即x方向以及y方向每间隔20mm布一个点，除去零点一共48个点.由于0°姿态角的雅可比条件数较好且没有输入的舍入误差，故下文均使用0°姿态角来验证运动学标定方法.

图3测量初始电机转角

Fig.3ThemeasurementoftheinitialmotorAngle

1—RRR反射球；2—磁性直角座；3—驱动杆；4—减速机

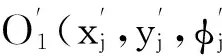
(4)根据式(6)、(7)计算出末端平台的姿态误差.最后将实验所得到的数据利用最小二乘法辨识模型的参数.

(6)

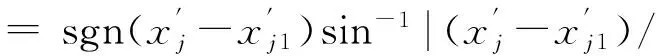
(7)

根据上述标定流程，使用考虑减速机背隙的运动学标定方法对实验所测得的数据进行处理，辨识出来的误差如表1所示.

表1考虑减速机背隙的运动学标定误差辨识结果

Table 1The result of error identification after kinematic calibration considering reducer backlash

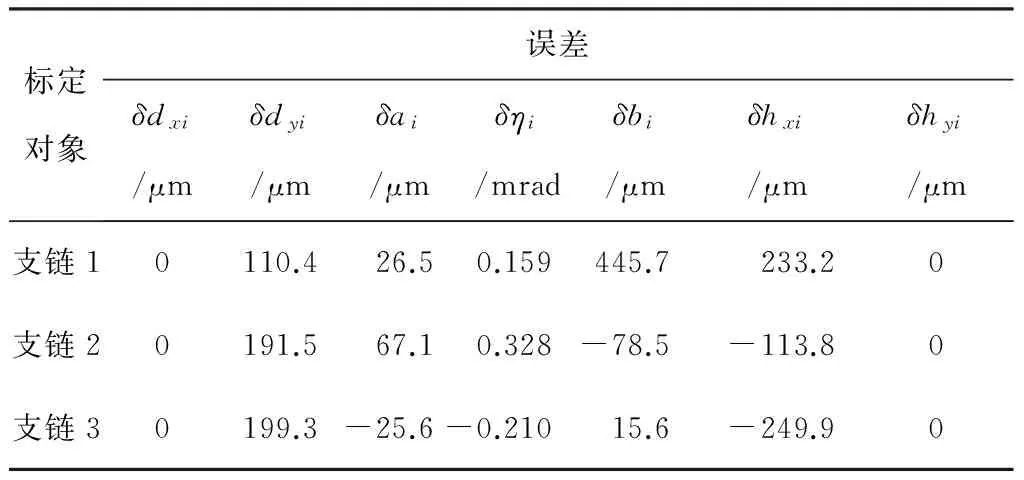
标定对象误差δdxi/μmδdyi/μmδai/μmδηi/mradδbi/μmδhxi/μmδhyi/μm支链10110.426.50.159445.7233.20支链20191.567.10.328-78.5-113.80支链30199.3-25.6-0.21015.6-249.90

通过表1可知，3处减速机的平均背隙分别0.159、0.328和-0.210 mrad.根据式(4)求解出3处减速机背隙对末端定位精度的影响，如图4所示.

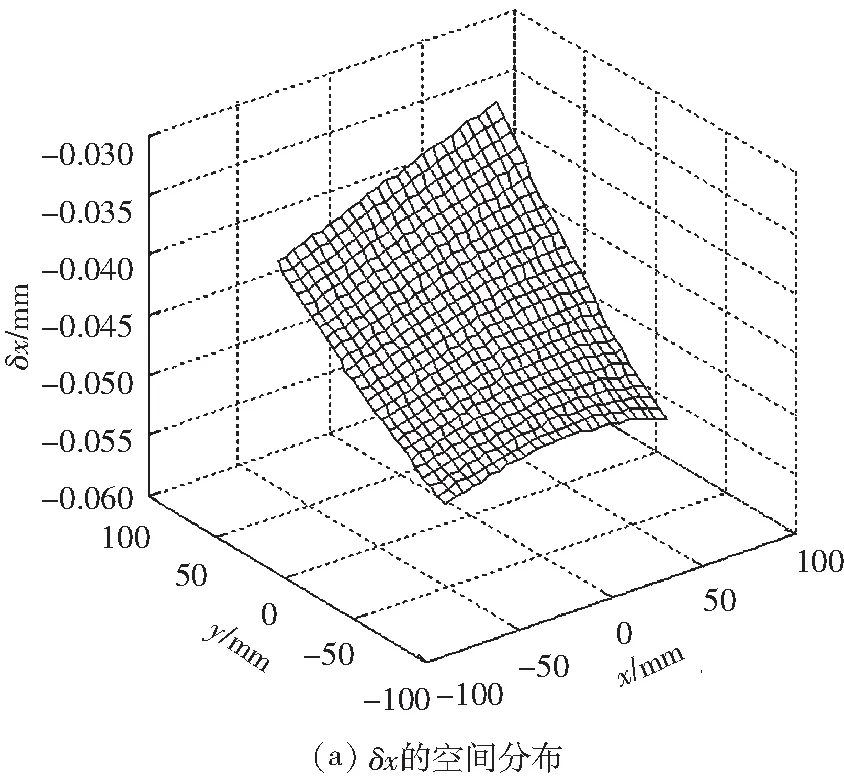
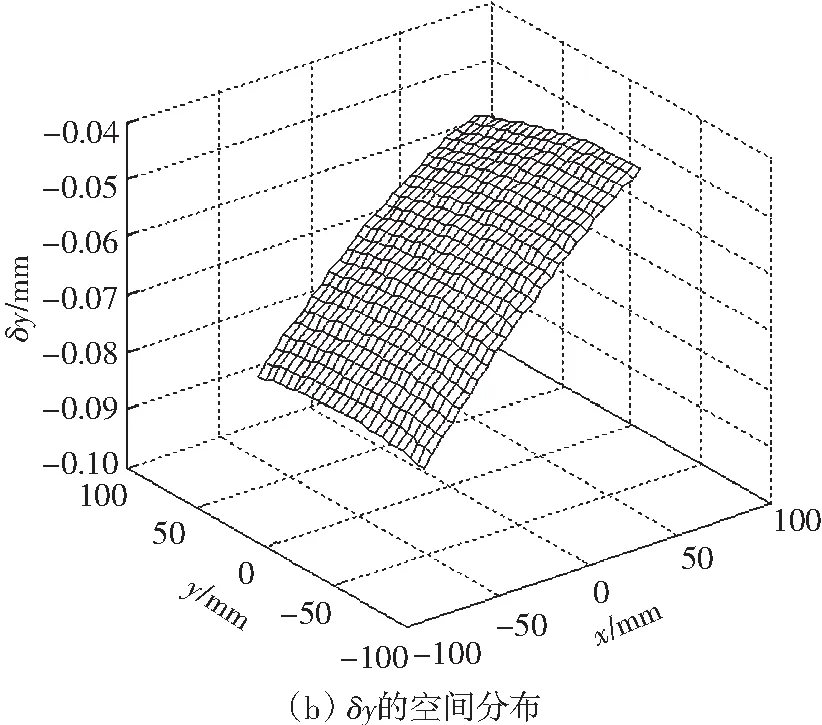
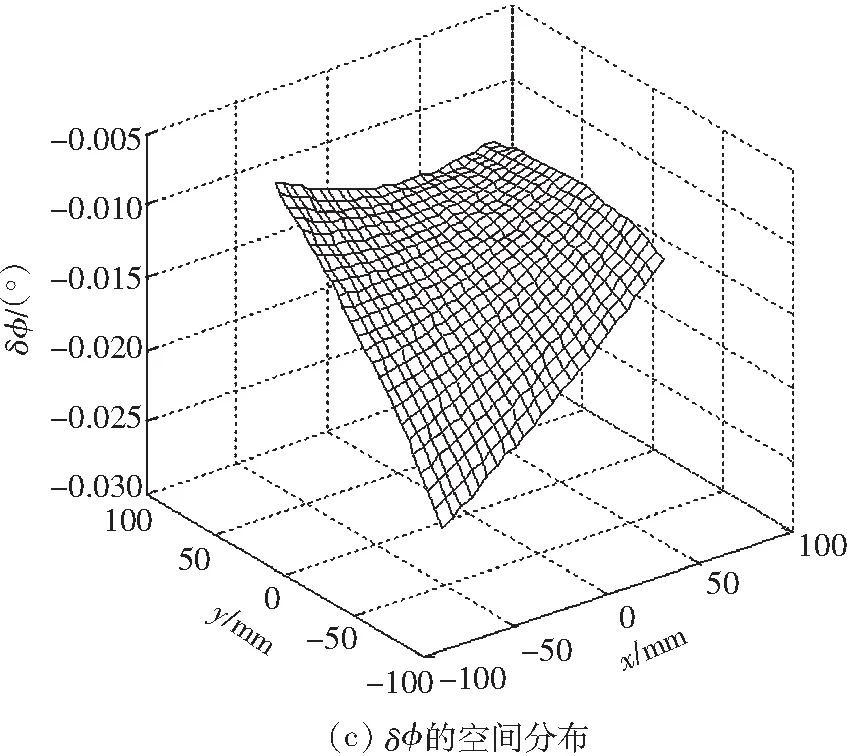
图4　减速机背隙引起的位姿误差

由图4可知减速机背隙引起的位姿误差相当大，x方向上造成的定位误差高达-0.05 mm，y方向上造成的定误差高达-0.08 mm，姿态角的偏差高达-0.02°；这一结果证明，减速机背隙不可忽略.

使用不考虑减速机背隙的运动学标定方法对实验数据进行处理，辨识出来的误差如表2所示.

表2不考虑减速机背隙的运动学标定误差辨识结果

Table 2The result of error identification after kinematic calibration without considering reducer backlash

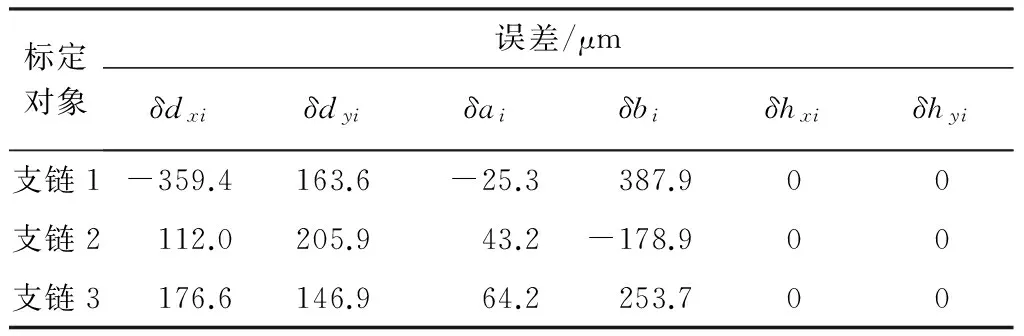
标定对象误差/μmδdxiδdyiδaiδbiδhxiδhyi支链1-359.4163.6-25.3387.900支链2112.0205.943.2-178.900支链3176.6146.964.2253.700

根据两者辨识的结果修正逆运动学模型，然后测量平面3-RRR并联机器人0°姿态角下末端平台的姿态误差的空间分布，如图5所示；其中，图(a)-(c)为未标定前的结果，图(d)-(f)为不考虑减速机背隙的运动学标定后的结果，图(g)-(i)为考虑减速机背隙的运动学标定后的结果.

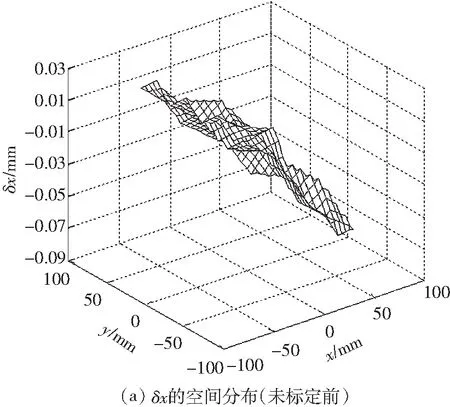
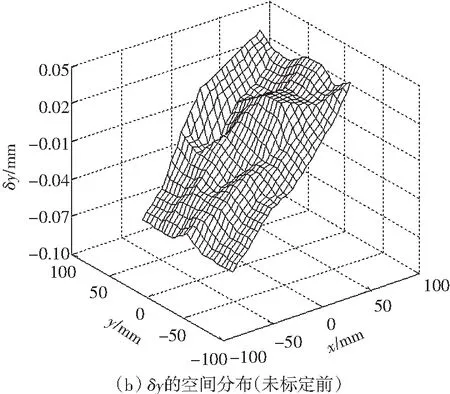
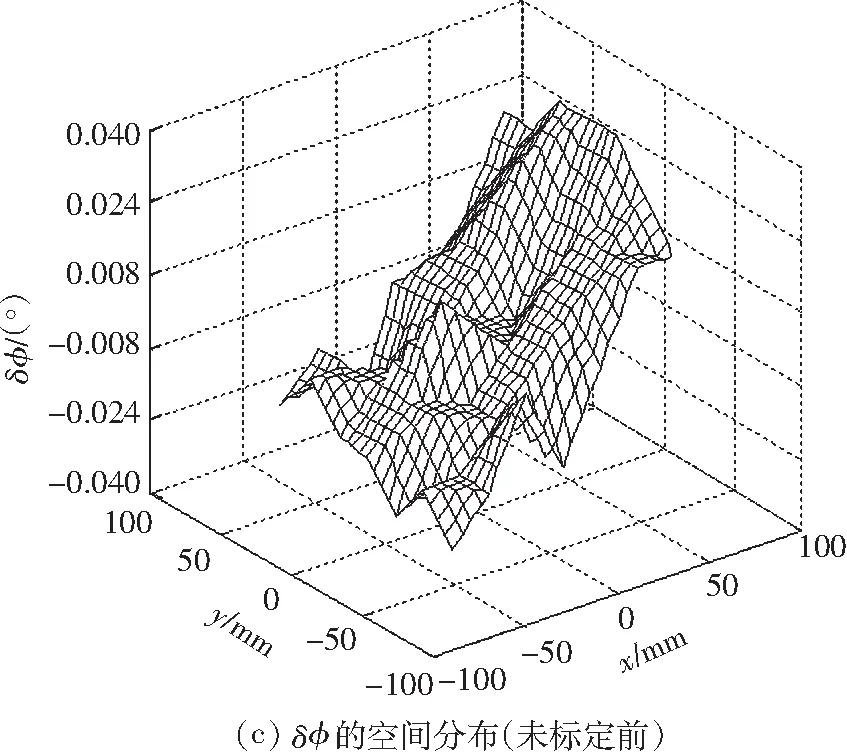
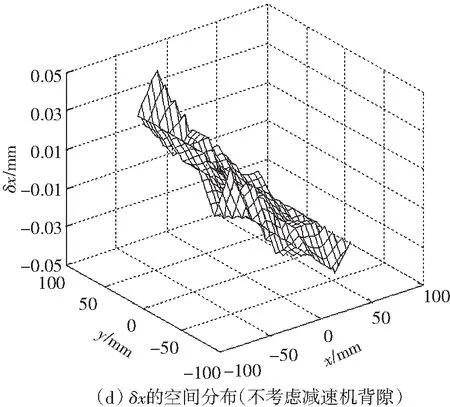
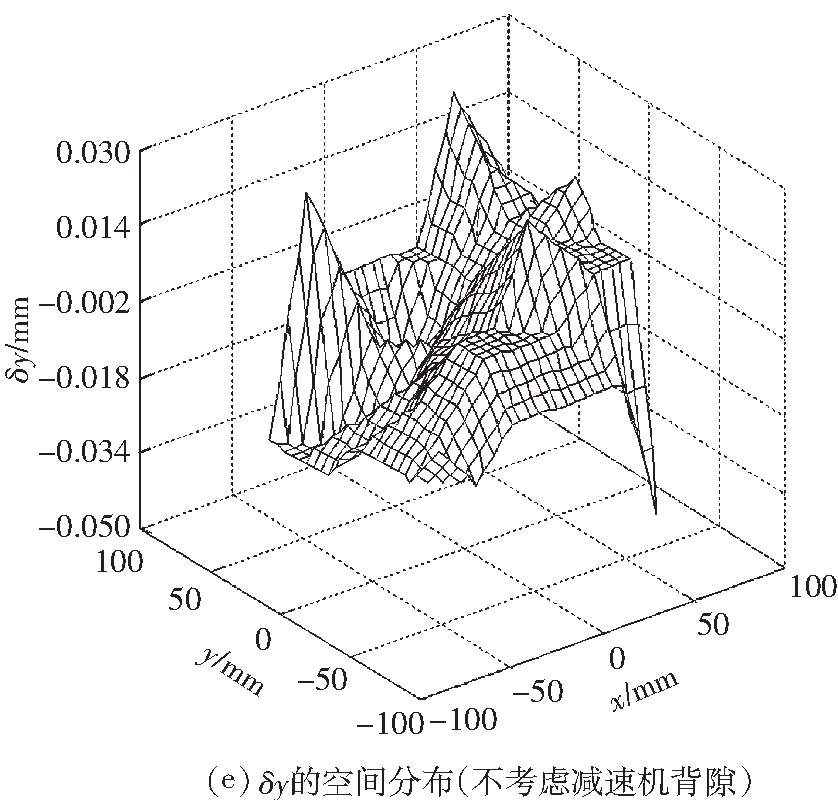
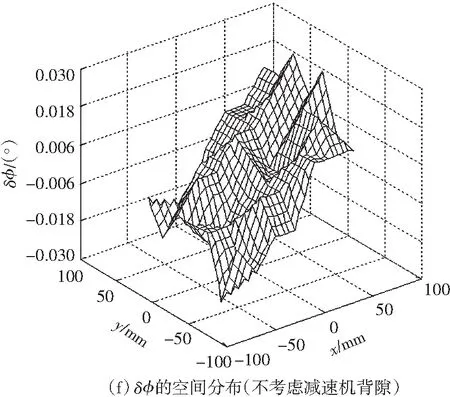
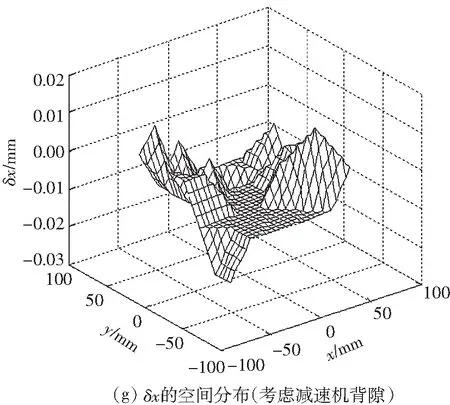
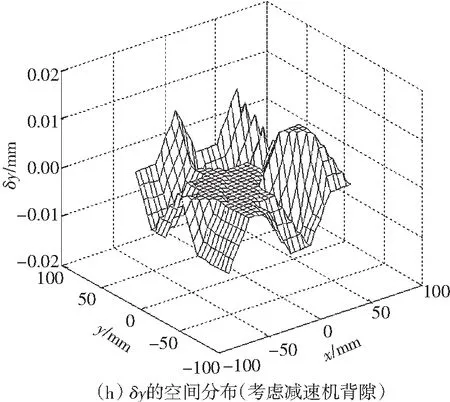
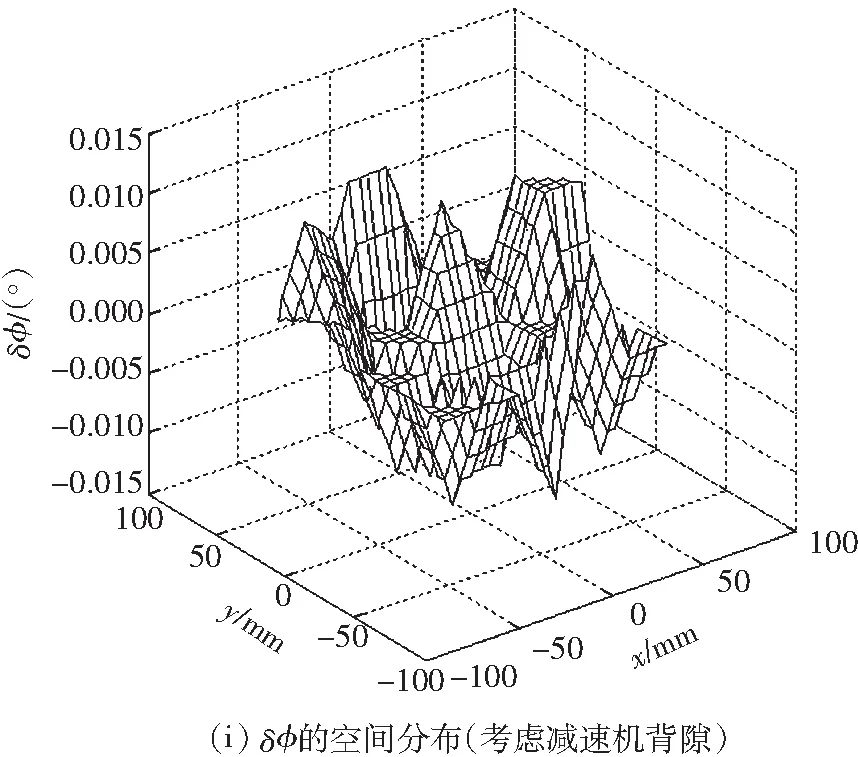
图5　0°姿态角下末端平台的位姿误差的空间分布

Fig.5The spatial distribution of the end-effector’s posture error under zero attitude angle

为了进一步提高平面3-RRR并联机器人的定位精度，根据前文所讲的误差补偿方法，使用上述测量到的样本点的姿态误差信息，添加误差补偿模块，然后再次测量其位姿误差的空间分布.文中仅对考虑减速机背隙的运动学标定方法得到的修正模型进行误差补偿.补偿后其位姿误差的空间分布如图6所示.

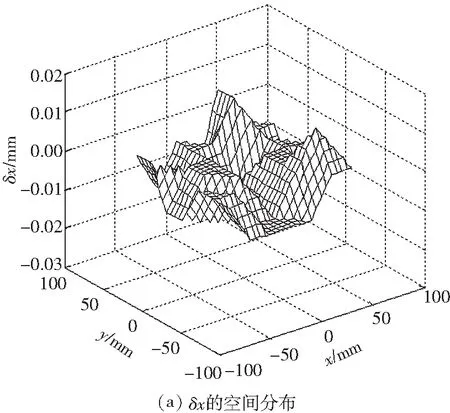
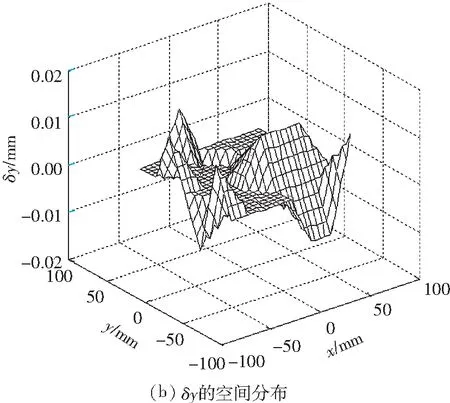
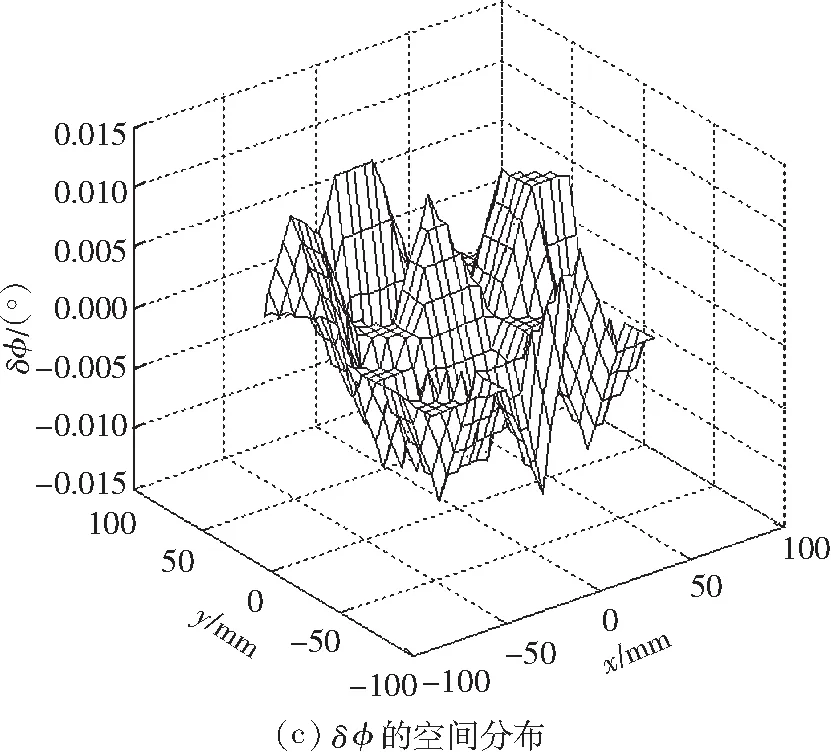
图6补偿后末端平台的位姿误差的空间分布

Fig.6The spatial distribution of the end-effector’s posture error after error compensation

由图6可知，经过补偿后末端平台在其工作空间内x方向的定位误差在±0.01 mm以内，y方向的定位误差在±0.01 mm以内，姿态角误差在±0.01°以内，故该补偿方法有效，能降低姿态误差的峰值，提高定位精度.从理论上讲，加入误差补偿模块，其姿态误差的空间分布总体上应该是平坦的，但是图6所示的并非如此.对于这个问题，原因有二：①激光跟踪仪的测量精度是0.01 mm，该平面3-RRR并联机器人的定位精度已经达到了激光跟踪仪所能测量的极限；②测量噪声的存在影响了测量结果.为了解决这个问题，下一步将尝试使用更高精度的测量设备或者对测量的数据进行滤波处理.

4　结语

通过考虑驱动端的减速机背隙对末端平台定位精度的影响，提出了考虑减速机背隙的误差模型，并利用最小二乘法辨识出该误差模型，最后加入误差补偿模块完成考虑减速机背隙的运动学标定.通过实验验证了考虑减速机背隙的运动学标定优于不考虑减速机背隙的运动学标定；对考虑减速机背隙的运动学标定方法得到的修正模型进行误差补偿后，x、y方向定位精度均控制在±0.01 mm以内，姿态角误差在±0.01°以内，该定位精度已然接近激光跟踪仪的测量精度，能够满足宏微结合中宏动平台定位精度的要求.

[1]莫嘉嗣，张宪民，邱志成，等.SEM环境下3PRR并联平台奇异区域规避与逃逸控制策略 [J].机械工程学报，2015，51(23)：1-11.

MO Jia-si，ZHANG Xian-min，QIU Zhi-cheng，et al.Control strategy research on avoid and escape the singular area of the 3PRR parallel platform based on SEM environment [J].Chinese Journal of Mechanical Engineering，2015，51(23)：1-11.

[2]AHMED J，MOHAMED S.Kinematic calibration of a 3-DOF planar parallel robot [J].Industrial Robot，2012，39(4)：392-400.

[3]JOUBAIR A，ZHAO L F，BIGRAS P,et al.Absolute accuracy analysis and improvement of a hybrid 6-DOF medical robot [J].Industrial Robot，2015，42(1)：44-53.

[4]TO M，WEBB P.An improved kinematic model for calibration of serial robots having closed-chain mechanisms [J].Robotica，2012，30(6)：963-971.

[5]GREENWAY B.Robot accuracy [J].Industrial Robot：An International Journal，2000，27(4)：257-265.

[6]ZHANG J，CHEN Q，WU C，et al.Kinematic calibration of a 2-DOF translational parallel manipulator [J].Advanced Robotics，2014，28(10)：707-714.

[7]NGUYEN H N，ZHOU J，KANG H J.A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network [J].Neurocomputing，2015，151(3)：996-1005.

[8]邵珠峰，唐晓强，王立平，等.平面柔性3-RRR并联机 构自标定方法 [J].机械工程学报，2009，45(3)：150-155.SHAO Zhu-feng，TANG Xiao-qiang，WANG Li-ping，et al.Self-calibration method of planar flexible 3-RRR parallel manipulator [J].Journal of Mechanical Engineering，2009，45(3)：150-155.

[9]马立，于瀛洁，程维明，等.BP神经网络补偿并联机器人定位误差 [J].光学精密工程，2008，16(5)：878-883.

MA Li，YU Ying-jie，CHENG Wei-ming，et al.Positioning error compensation for a parallel robot based on BP neural networks [J].Optics and Precision Engineering，2008，16(5)：878-883.

[10]JUDD R P，KNASINSKI A B.A technique to calibrate industrial robots with experimental verification [J].IEEE Transactions on Robotics and Automation，1990，6(1)：20-30.

[11]SLAMANI M，NUBIOLA A，BONEV I A.Modeling and assessment of the backlash error of an industrial robot [J].Robotica，2012，30(7)：1167-1175.

[12]张宪民，刘晗.3-RRR并联机器人含间隙的运动学标定及误差补偿 [J].华南理工大学学报(自然科学版)，2014，42(7)：97-103.

ZHANG Xian-min，LIU Han.A clearance approach of calibration and error compensation for a 3-RRR parallel robot [J].Journal of South China University of Technolo-gy (Natural Science Edition),2014，42(7)：97-103.

[13]张清华.平面3-RRR柔性并联机器人机构弹性动力学建模与振动主动控制研究 [D].广州：华南理工大学机械与汽车工程学院，2013.

[14]黄兴，何文杰，符远翔.工业机器人精密减速器综述 [J].机床与液压，2015，43(13)：1-6.

HUANG Xing，HE Wen-jie，FU Yuan-xiang.Summary of precision speed reducer of industrial robots [J].Machine Tool & Hydraulics,2015，43(13)：1-6.

[15]胡鹏浩，宋昆鹏.一种平面3RRR并联机器人结构参数识别 [J].制造业自动化，2005，27(10)：41-43.

HU Peng-hao，SONG Kun-peng.The structure parameter calibration of a planar 3RRR manipulator [J].Manufacturing Automation，2005，27(10)：41-43.

[16]谢平，刘志杰，杜义浩.基于蚁群算法的并联机器人误差补偿方法 [J].计算机工程，2011，37(16)：11-13.

XIE Ping，LIU Zhi-jie，DU Yi-hao.Error compensation method of parallel robot based on ant colony algorithm [J].Computer Engineering,2011，37(16)：11-13.

[17]靳国栋，刘衍聪，牛文杰.距离加权反比插值法和克里金插值法的比较 [J].长春工业大学学报(自然科学版)，2003，24(3)：53-57.

JIN Guo-dong，LIU Yan-cong，NIU Wen-jie.Comparison between inverse distance weighting method and kriging [J].Journal of Changchun University of Technology(Natural Science Edition),2003，24(3)：53-57.

s： Supported by the National Natural Science Foundation of China(U1501247)and the Science and Technology Research Projects of Guangdong Province(2014B090917001，2015B020239001)

Kinematic Calibration of 3-RRR Parallel Mechanism Considering Reducer Backlash

ZHANGXian-minZENGLei

(School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510640，Guangdong，China)

In order to improve the positioning accuracy of macro parallel platforms，firstly，an error model of 3-RRR parallel mechanism，which takes into consideration the reducer backlash，is derived，and the effectiveness of the proposed model is verified through a comparison with the error model without considering the reducer backlash. Secondly，an experiment is carried out to measure the attitude error of end-effector and to identify the parameters of the two above-mentioned models. Then，IDWM is employed to realize spatial interpolation and error compensation，followed with a kinematic calibration. Finally，the inverse kinematic model is corrected according to kinematic calibration results. It is found from the measured posture error distribution of end-effector that the proposed error model considering reducer backlash is superior to that without considering the backlash. The kinematic calibration conside-ring reducer backlash enhances the positioning accuracy of parallel mechanism and provides a theoretical foundation for the development of high-precision macro-micro parallel mechanisms.

parallel platform； reducer backlash； kinematic calibration； IDWM； posture error； positioning accuracy

1000-565X(2016)07-0047-08

2015-11-25

国家自然科学基金资助项目(U1501247)；广东省科技攻关项目(2014B090917001，2015B020239001)

张宪民(1964-)，男，教授，博士生导师，主要从事机构学、精密制造装备与现代化控制技术研究.E-mail：zhangxm@scut.edu.cn

TP 242doi： 10.3969/j.issn.1000-565X.2016.07.008