液力变矩器动态循环流量的传递函数表征法*

李文嘉　王安麟　孟庆华　李晓田　韩继斌

(1.同济大学 机械与能源工程学院，上海 201804； 2.山推工程机械股份有限公司，山东 济宁 272073)



液力变矩器动态循环流量的传递函数表征法*

李文嘉1王安麟1孟庆华1李晓田1韩继斌2

(1.同济大学 机械与能源工程学院，上海 201804； 2.山推工程机械股份有限公司，山东 济宁 272073)

为快速求解液力变矩器循环流量的动态响应，提出液力变矩器动态循环流量的传递函数表征法.该方法基于一元束流理论的推导，以确定结构形态的液力变矩器为对象，将动态循环流量视为以静态循环流量为输入的一阶线性系统的响应，通过液力变矩器常用工况范围内的简单工况CFD(计算流体动力学)静态、动态仿真数据，构建动态循环流量系统的传递函数.仿真结果表明：此方法对液力变矩器常用工况范围内的动态循环流量的预测拟合优度达到0.987，对输入、输出轴动态扭矩的预测拟合优度达到0.95；相对于CFD仿真，此方法在小幅牺牲计算精度的同时大幅提升了计算速度，是一种快速求解液力变矩器动态响应的有效方法.

液力变矩器；动态循环流量；传递函数；计算流体动力学仿真；一元束流理论

液力变矩器是土方机械和汽车传动系统的重要零部件.在实际作业中，液力变矩器经常处于非稳态工况，如车辆起步、铲掘等工况.液力变矩器在非稳态工况下的响应与稳态时有很大区别.同时，整机实际作业时，液力变矩器的效率有较大提升空间.因此，其动态性能的工程化设计有重要意义.

对液力变矩器动态性能的研究方法可以分为3类.第一类是基于计算流体力学(CFD)仿真的研究，Yamaguchi、Yue等[1-2]分别用CFD研究不同工况下液力变矩器的性能，并用实验证明预测精度；王安麟等[3-4]等根据CFD动态、静态仿真，设计叶片厚度、叶片数，取得较好效果；杨健等、刘春宝等[5-6]证明了液力变矩器的CFD动态仿真与实验误差较小；Liu等[7]利用CFD研究液压油温度对液力变矩器性能的影响.以上这些研究证明了CFD动态仿真的精度，但由于大自由度流固耦合求解时间的限制，难以实现动态性能快速响应.第二类是基于一元束流理论的研究，Barglazan、李丽丽等[8-9]根据一元束流理论建立了不同形式的液力变矩器动态数学模型；Chen等[10]等根据一元束流理论建立模型，并引入遗传算法优化变矩器与发动机的匹配，由于一元束流存在诸多简化，这些研究难以保证计算的准确性.第三类是将液力变矩器视为一个系统进行研究，赵红等[11-12]依照实验进行系统辨识，将三元件液力变矩器这一非线性系统分解成多段线性系统，系统难以同时满足简洁性和精确性；Robinette 等[13]将液力变矩器简化为线性弹簧-质量-阻尼模型，模型参数由泵轮转速确定，但其缺乏简化的理论依据.综上，液力变矩器快速高精度的动态响应求解问题仍然没有解决.

为解决上述问题，本研究在指出动态循环流量是液力变矩器动态响应核心问题的基础上，从工程角度出发，提出液力变矩器动态循环流量的传递函数表征法(以下简称“传递函数法”)；以工程实际应用的某型号双涡轮液力变矩器为例，验证传递函数法的可行性；用传递函数法预测动态循环流量和输入、输出轴动态扭矩，验证传递函数法的有效性.

1　传递函数法

文中提出的传递函数法以一元束流理论和系统论为理论支撑，辅助CFD仿真以保证精度.该方法首先根据一元束流理论的推导，指出动态循环流量是液力变矩器动态响应的核心问题；然后根据系统论及简化，将动态循环流量视为以静态循环流量为输入的一阶线性系统的响应；接着用有限次CFD静态仿真数据标定一元束流理论中的参数，得到根据工况快速、高精度计算静态循环流量的公式；最后用简单工况的CFD动态仿真数据及工况对应的静态循环流量反求一阶线性系统的传递函数.

1.1液力变矩器的动态响应

液力变矩器的动态响应是指液力变矩器对于非稳态工况的响应，动态方程是研究动态响应的基础.液力变矩器动态方程的自变量、因变量与液力变矩器转速、扭矩的对应关系并没有绝对要求[11]，文中采用与一元束流理论相同的设定，即以各叶轮转速作为自变量、扭矩作为因变量.

根据牛顿定律，叶轮动态扭矩如式(1)[14]：

(1)

其中：下标j表示叶轮，对于双涡轮液力变矩器，其可以为B、T1、T2、D，分别表示泵轮、第一涡轮、第二涡轮、导轮，下同；MD表示叶轮所受扭矩；MH表示叶轮所受液力扭矩；J表示叶轮及其轴的转动惯量；JY表示叶轮内部工作液体的转动惯量；ω表示叶轮转速.

文中进行CFD仿真时，将叶栅作为仿真流道限制面考虑，因此不考虑叶轮及其轴的转动惯量：

Jj=0

(2)

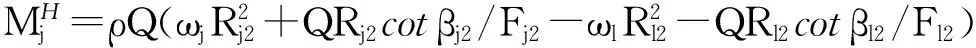
(3)

其中：下标l表示在工作介质流动方向上，叶轮j的前一个叶轮；ρ表示变矩器内液体密度；Q表示循环流量；R表示叶轮进出口半径；β表示叶轮进出口液流角；F表示叶轮进出口法相面积；下标1、2分别表示叶轮进口和出口.

上述除循环流量外，其他参数都与变矩器几何形态直接相关，对于确定的液力变矩器，可以近似认为为定值.因此，只要得到液力变矩器循环流量的动态响应，即可得到液力变矩器的动态扭矩响应.

1.2液力变矩器动态循环流量

液力变矩器的循环流量是变矩器内工作液体在压力差作用下流动产生的结果，液力变矩器内工作液体压力差按式(4)计算[15]：

(4)

其中：p、pc和pm分别表示叶轮给液体增加的压力、叶轮内液体由于冲击而损失的压力和叶轮内液体由于摩擦而损失的压力，其公式如文献[15]所述.

引入液感表征液体在压力差作用下增减速的惯性，则有式(5)：

(5)

其中，L表示液感，对于确定的流体和流道，液感可以近似认为为定值.将式(4)代入式(5)，经过化简，可得式(6)：

fωjωl)

(6)

其中，a、b、c、d、e、f与变矩器几何形态、液体密度和冲击、摩擦损失系数相关[15].

式(6)是动态循环流量的微分方程，结合系统论知识可知，式(6)表征一个以4个叶轮转速为输入、动态循环流量为输出的多输入单输出非线性系统，文中把这个系统称为“动态循环流量系统”.对于非线性系统，难以建立精确的数学模型.但对于确定且平稳无噪声的非线性系统，可以利用相空间重构原理[16]，重构一个等价的线性状态空间，即以一个等价的线性系统近似代替原系统.

直接求解多输入系统难度较大.但由静态循环流量公式可知，对于任何工况，都存在一个循环流量，使式(4)为0，记这个循环流量为静态循环流量Qs，由Qs的定义可知，其与4个叶轮转速存在对应关系，因此可以将上述多输入单输出系统转化为以Qs为输入、以动态循环流量Q为输出的单输入单输出的系统，此系统便于求解.对于这样一个系统，可以用传递函数加以描述，如式(7)：

(7)

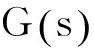
在式(6)中，动态循环流量对时间微分项最高是一次的，因此系统是一阶的.经过一元束流理论的推导和基于系统论的简化，动态循环流量可以视为以静态循环流量为输入的一阶线性系统的响应.

这里必须指出，经过非线性系统向线性系统的简化以及多输入系统向单输入系统的简化，新系统与原系统的动态响应存在一定误差，但后续研究证明，在液力变矩器常用工况范围内，新系统动态响应误差足够小，满足工程需要.

1.3液力变矩器静态循环流量

式(4)为0时，表示液体流速稳定，此时的循环流量是静态循环流量.在此条件下化简式(6)，可得式(8).其中：a、b、c、d、e、f、o、p与变矩器几何形态、液体密度和冲击、摩擦损失系数相关，当传动比一定时，可以认为是定值[15].

(8)

传动比一定，且小于工况转换点传动比时，第一涡轮、第二涡轮转速与泵轮转速的关系如式(9)-(10)所示：

ωT1=iωBi1

(9)

ωT2=iωBi2

(10)

其中，i表示变矩器传动比，i1和i2分别表示变矩器输出轴与第一涡轮和第二涡轮间齿轮副的传动比.将式(9)-(10)代入式(8)，则可以得到关于Qs的一元二次方程，求解这个方程，可以得到静态循环流量Qs的表达式，如式(11)所示.由式(11)可知，当传动比一定，且小于工况转换点传动比时，静态循环流量与泵轮转速成正比.

Qs={-(b+cii1+dii2)+[(b+cii1+dii2)2-

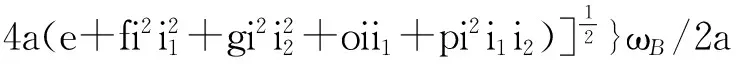
(11)

当传动比一定，且大于工况转换点传动比时，第一涡轮脱转.CFD静态仿真表明，脱转时，第一涡轮转速与泵轮转速成正比.根据类似于式(11)的推导可知，静态循环流量与泵轮转速成正比.

综上，当传动比一定时，静态循环流量与泵轮转速成正比，可用式(12)表示：

Qs=kiωB

(12)

其中，ki为静态循环流量与泵轮转速的比例系数(以下简称“比例系数”).不同传动比对应不同的比例系数，求出足够多传动比下的比例系数，其余传动比下的比例系数用其相近两传动比下的比例系数进行差值，可以保证计算精度.利用式(12)可以根据工况快速计算静态循环流量，而无需再进行额外的CFD仿真.

2　动态循环流量系统的传递函数

以工程实际应用的某型号液力变矩器为例进行研究，其循环圆直径为315mm，根据其静态循环流量和对应的动态循环流量反求系统传递函数，以验证传递函数法的可行性.

2.1CFD仿真精度

由于实验测量液力变矩器循环流量存在较大难度，且CFD仿真精度较高[1-6]，因此，文中采用CFD仿真结果标定传递函数法中的相关系数.针对文中所用的液力变矩器，其台架实验和CFD仿真对比如图1所示.平均相对误差按式(13)计算：

(13)

其中，x表示仿真值，μ表示实验值，n表示实验编号，m表示实验次数.由式(13)计算可以得到变矩比和效率的平均相对误差分别为3%和2%，由此可知CFD仿真与实验之间的误差较小.

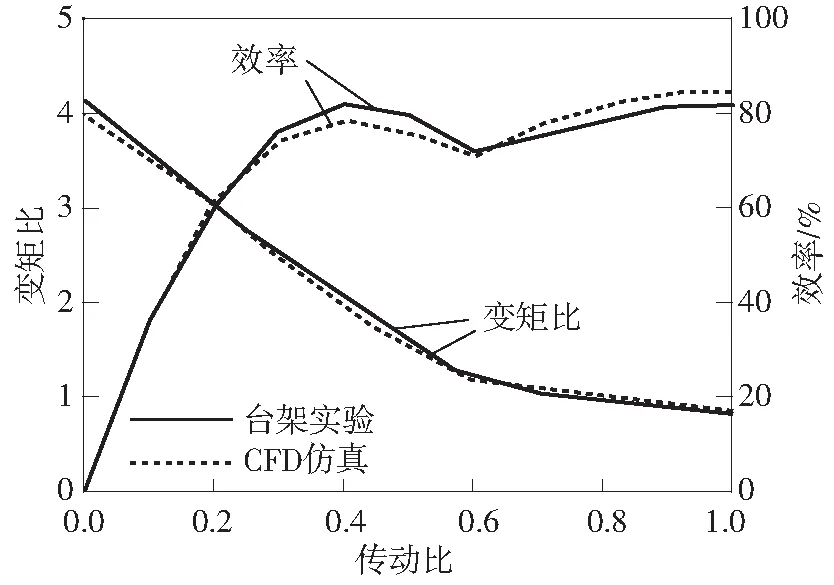
图1台架实验与CFD仿真对比

Fig.1Comparison of platform experiment and CFD simulation

2.2静态循环流量

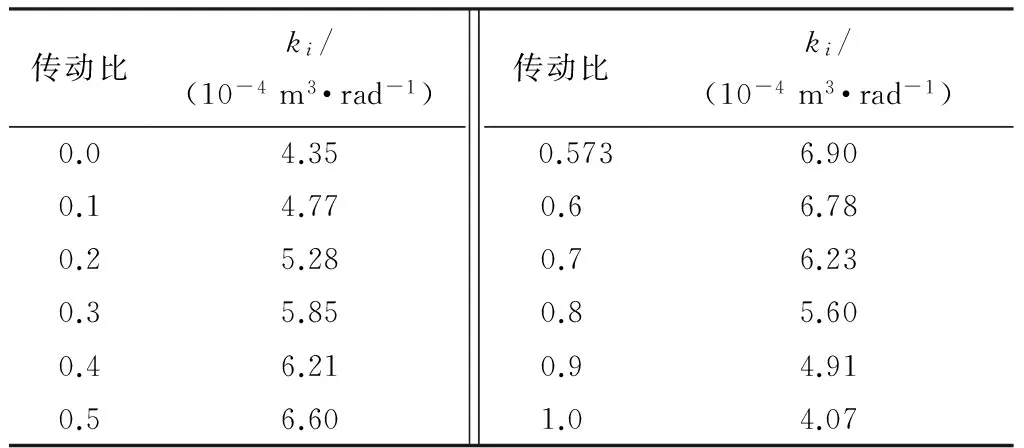
由式(12)可知，静态循环流量由泵轮转速和传动比决定，可以根据有限次静态CFD仿真数据获得不同传动比下的比例系数.根据液力变矩器实际作业的工况范围选取工况采样点，并进行CFD静态仿真，得到不同传动比下的比例系数，如表1所示.

表1不同传动比下静态循环流量与泵轮转速的比例系数

Table 1Proportional coefficient of static circulating flow rate and pump rotational speed in different transmission ratios

传动比ki/(10-4m3·rad-1)0.04.350.14.770.25.280.35.850.46.210.56.60传动比ki/(10-4m3·rad-1)0.5736.900.66.780.76.230.85.600.94.911.04.07

根据表1的比例系数，静态循环流量可以直接由工况求得，无需进行CFD静态仿真.由式(13)可知，此方法计算得到的静态循环流量与CFD静态仿真结果的平均相对误差为0.074%，满足工程精度要求.

2.3动态循环流量

动态循环流量可以根据CFD动态仿真数据获得.CFD动态仿真工况设置如图2所示，其由一系列阶跃工况组成，以方便求解系统传递函数；且每段稳定工况的泵轮转速和传动比都是变矩器正常作业的极限值，以保证动态循环流量系统的适用范围.

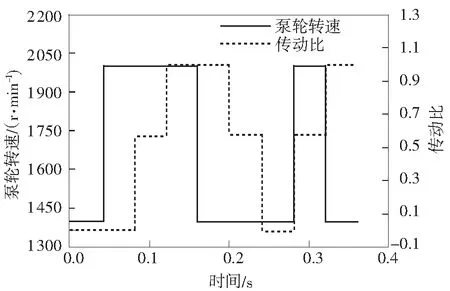
图2CFD动态仿真工况设置

Fig.2Working condition setting of CFD dynamic simulation

根据工况设置进行CFD动态仿真，可以得到动态循环流量，如图3所示.

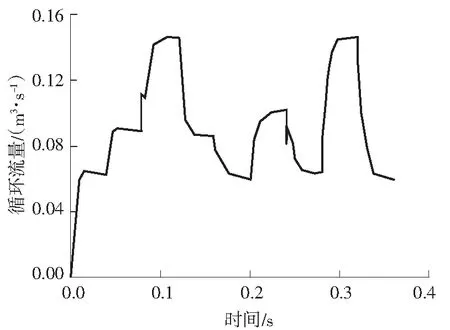
图3动态循环流量

Fig.3Dynamic circulating flow rate

2.4动态循环流量系统的传递函数

动态循环流量系统的输入可以根据式(12)、表1及图2所示的CFD动态仿真工况获得，输出可以从CFD仿真数据直接得到.动态循环流量系统的输入和输出如图4所示.

需要说明的一点是：仿真初始阶段，变矩器从静止阶跃到泵轮转速1 400 r/min，由于变矩器静止工况不属于变矩器正常工作工况，所以不在文中建立的静态模型考虑工况范围内.因此，仿真的第一段稳定工况不用于后续研究.在文中第3节的预测工况中，仿真的第一段同样不用于研究.

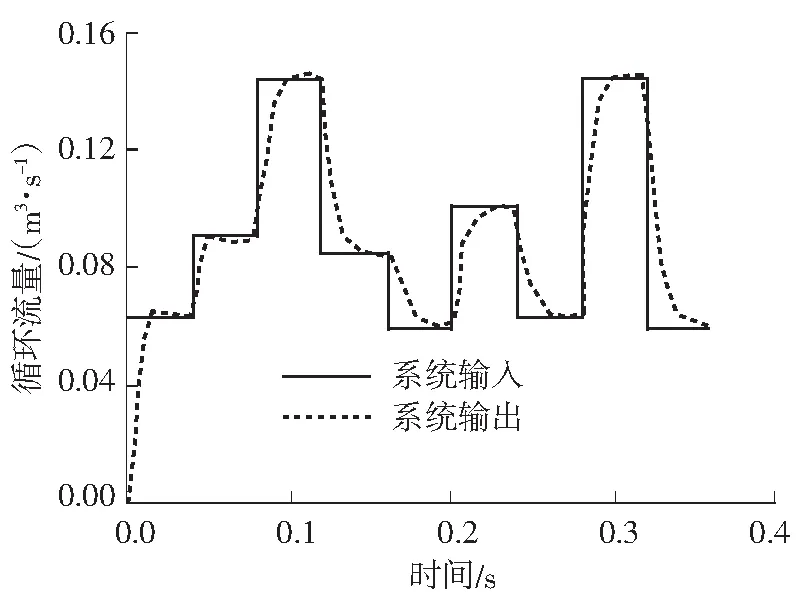
图4动态循环流量系统的输入和输出

Fig.4Input and output of dynamic circulating flow rate system

已知系统输入和输出，且已知系统传递函数形式，则可以求解系统传递函数.求解结果如式(14)：

(14)

用此传递函数及静态循环流量计算得到的动态循环流量与CFD动态仿真结果的对比如图5所示，两者拟合优度达到0.975，精度较高.

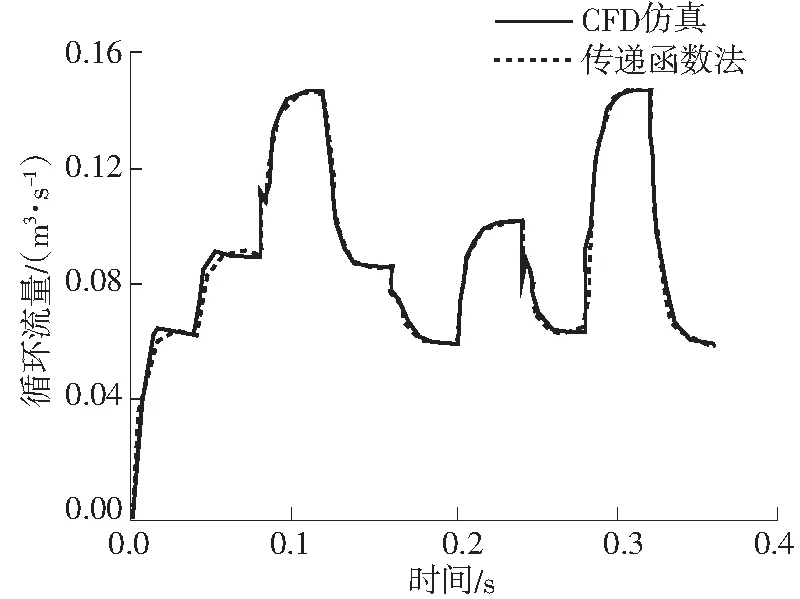
图5传递函数法与CFD动态仿真计算的动态循环流量

Fig.5DynamiccirculatingflowratecalculatedbytransferfunctionmethodandCFDsimulation

3　传递函数法有效性的验证

用前文得到的传递函数预测液力变矩器动态循环流量和输入、输出轴动态扭矩，并与CFD动态仿真结果进行对比，以验证传递函数法的有效性.

3.1动态循环流量的预测

为预测动态循环流量，需建立一组新的工况，称为“预测工况”.预测工况与求解传递函数时所用的工况不同，才可以证明传递函数对工况的适用范围.根据这个原则，设置如图6所示的预测工况.

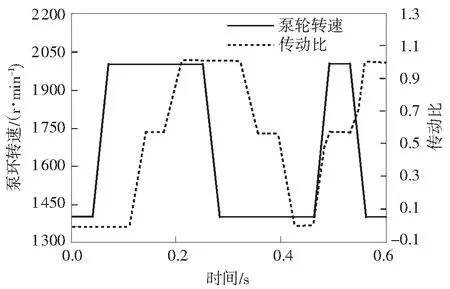
图6预测工况的工况设置

Fig.6Working condition setting of prediction condition

在此工况下，传递函数对于动态循环流量的预测结果与CFD动态仿真得到的循环流量如图7所示，两者的拟合优度达到0.987.

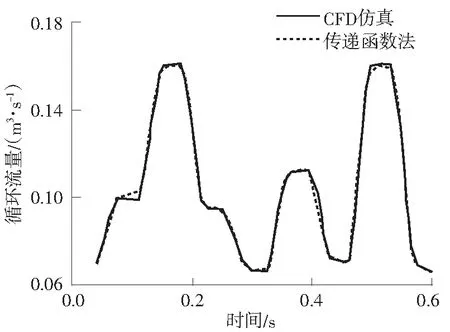
图7CFD仿真与传递函数法预测的动态循环流量对比

Fig.7Comparison of dynamic circulating flow rate calculated by CFD simulation and that predicted by transfer function

3.2输入、输出轴动态扭矩的预测

将式(7)、(3)、(2)代入式(1)，经过化简，可得叶轮动态扭矩公式，如式(15)所示：

(15)

对于工作液体和结构确定的液力变矩器，液体密度、几何尺寸以及叶轮内工作液体转动惯量可以认为是定值.若根据一元束流理论直接正向求解上述各物理量会带来较大的计算误差，因此文中根据CFD静态仿真及动态仿真数据反求上述物理量.

对于几何参数和液体密度，反求的基本方法是：对于某工况的静态CFD仿真，各叶轮转速、静态扭矩及循环流量可以从设置或仿真数据得到，因此式(3)中的未知量就只有几何参数和液体密度，可以列出一个关于几何参数和液体密度的方程；根据多个工况的静态CFD仿真数据，可以列出多个方程，组成方程组，求出这些系数的最小二乘解.求解结果如表2所示.用此最小二乘解及式(3)计算得到的输入、输出轴静态扭矩与CFD静态仿真数据相比，平均误差为3.39%，满足工程精度要求.

表2几何参数及液体密度的最小二乘解

Table2Leastsquaresolutionofgeometricparameterandliquiddensity

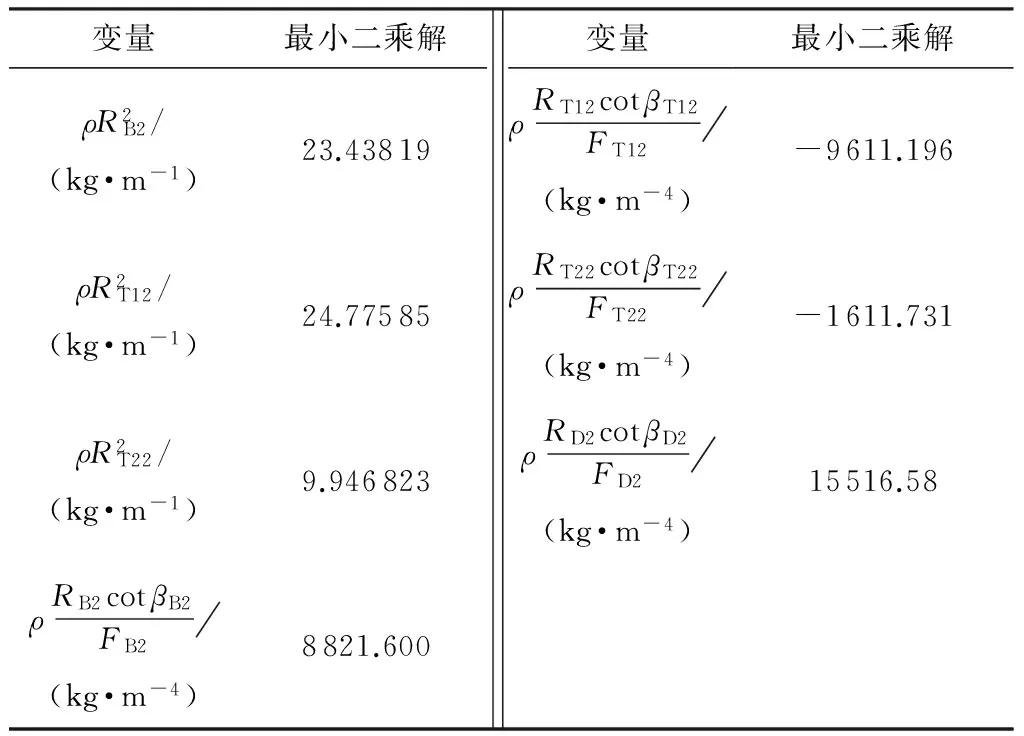
变量最小二乘解ρR2B2/(kg·m-1)23.43819ρR2T12/(kg·m-1)24.77585ρR2T22/(kg·m-1)9.946823ρRB2cotβB2FB2(kg·m-4)8821.600变量最小二乘解ρRT12cotβT12FT12(kg·m-4)-9611.196ρRT22cotβT22FT22(kg·m-4)-1611.731ρRD2cotβD2FD2(kg·m-4)15516.58

对于旋转叶轮内液体的转动惯量，可以根据阶跃工况中，工况突变时扭矩增量、转速增量和仿真步长获得.泵轮、第一涡轮、第二涡轮内液体的转动惯量分别为2.415 1×10-4、0.503 31×10-4、1.699 5×10-4kg/m2.

将表2所示结果、3个旋转叶轮内液体的转动惯量及式(14)代入式(15)，则可以得到传递函数法求得的各叶轮的液力动态扭矩公式.在预测工况下，对比传递函数法预测的输入、输出轴动态扭矩与CFD动态仿真得到的输入、输出轴动态扭矩，如图8所示，输入轴扭矩和输出轴扭矩的拟合优度分别达到0.966和0.934.

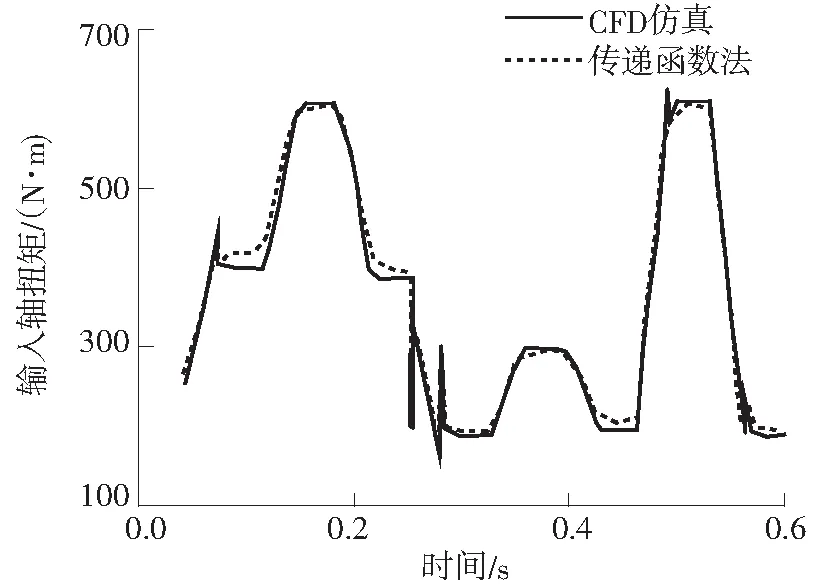
(a)输入轴扭矩对比

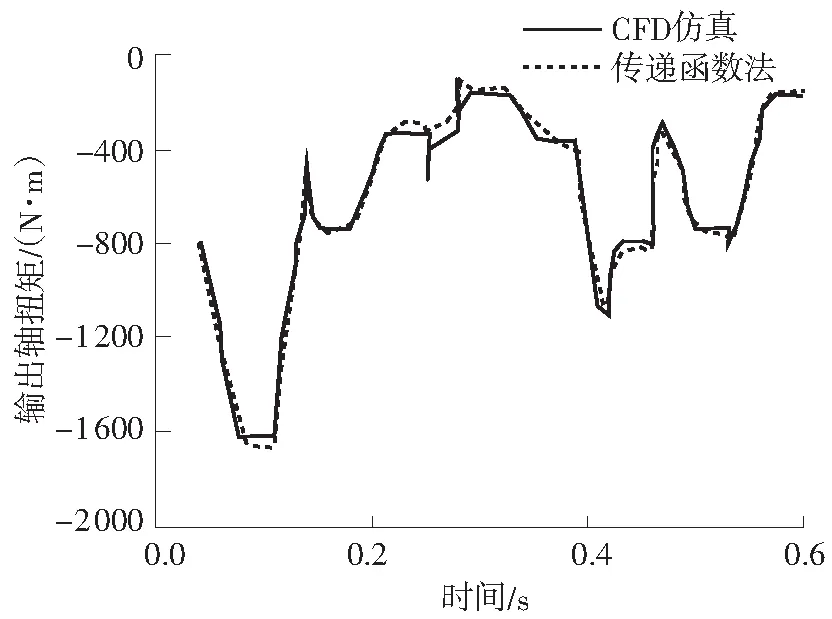
(b)输出轴扭矩对比

Fig.8Comparison of dynamic torque predicted by transfer function and that calculated by CFD simulation

4　结语

本研究从工程角度出发，将液力变矩器视为一个系统，提出以传递函数表征液力变矩器动态特性的方法，给出工程化求解液力变矩器动态循环流量快速响应流程，并以工程实际应用的某型号液力变矩器为例，根据传递函数法构建动态系统传递函数模型，验证该方法的可行性；结果表明，用传递函数法构建的动态系统传递函数模型对液力变矩器的动态循环流量和输入、输出轴动态扭矩进行预测，三者拟合优度分别达到0.987，0.966和0.934，验证了该方法的有效性.文中提出的传递函数法对求解各种形式的液力变矩器的动态循环流量响应具有普适性，但用此法求出的传递函数仅适用于特定研究对象.

[1]YAMAGUCHI T，TANAKA K.Torque converter transient characteristics prediction using computational fluid dynamics [J].Earth and Environmental Science,2012,15(4):1-7.

[2]YUE L.Characteristics prediction of torque converter based on CFD [C]∥2011 International Conference on Electronics，Communications and Control.New York：IEEE，2011：4203-4206.

[3]WANG A，LIU W，LONG G.Design method of blade thickness based on fluid-structure interaction of hydrodynamic torque converter [J].Journal of Tongji University，2015，43(4)：599-604.

[4]王安麟，孟庆华，曹岩，等.液力变矩器的叶片数神经网络模型 [J].西安交通大学学报，2015，49(7)：11-16.

WANG An-lin，MENG Qing-hua，CAO，Yan，et al.Blade number neural networks model of hydraulic torque converter [J].Journal of Xi’an Jiaotong University，2015，49(7)：11-16.

[5]杨健，苏华山，刘军辉，等.变泵轮转速液力变矩器动态特性数值模拟 [J].液压与气动，2014(12)：44-47.

YANG Jian，SU Hua-shan，LIU Jun-hui，et al.Dynamic performance analysis of hydraulic torque converter for pump impeller rotational speed [J].Chinese Hydraulics & Pneumatics，2014(12)：44-47.

[6]刘春宝，马文星，朱喜林，等.液力变矩器三维瞬态流场计算 [J].机械工程学报，2010，46(14)：161-166.

LIU Chun-bao，MA Wen-xing，ZHU Xi-lin，et al.3D transient calculation of internal flow field for hydrodynamic torque converter [J].Chinese Journal of Mechanical Engineering，2010，46(14)：161-166.

[7]LIU Z，LI Z，XIA G.Research on effect of working oil temperature for hydraulic torque converter performance using CFD and test [J].Journal of Mechanical Enginee-ring，2014，6：118-125.

[8]BARGLAZAN M.Dynamic identification of a hydrodynamic torque converter [J].University “Politehnica” of Bucharest，Scientific Bulletin Series D：Mechanical Engineering，2010，72(4)：225-234.

[9]李丽丽，何玉林，李成武，等.导叶可调式液力变矩器在大型风电机组传动系统中的动态仿真研究 [J].机械制造，2007，45(4)：17-19.

LI Li-li，HE Yu-lin，LI Cheng-wu，et al.Dynamic simulation study of hydrualic torque convertor with adjustable stator blade used in large wind turbines transmission system [J].Machinery，2007，45(4)：17-19.

[10]CHEN K，WU G.Genetic algorithm-based multi-objective optimization for the matching of torque converter with engine [J].Automotive Engineering，2014，5：532-536.

[11]赵红，马文星，王大志，等.液力变矩器动态特性辩识方法的探讨 [J].工程机械，2002，33(7)：28-31.ZHAO Hong，MA Wen-xing，WANG Da-zhi，et al.Experi-mental identification of the dynamic behavior of hydrodynamic torque convertor [J].China Mechanical Engineering，2002，33(7)：28-31.

[12]赵红，霍炜，马文星，等.液力变矩器动态特性辨识实验研究 [J].青岛大学学报(工程技术版)，2001，16(1)：6-10.

ZHAO Hong，HUO Wei，MA Wen-xing，et al.A study on the identification method of dynamic characteristics of hydraulic torque converter [J].Journal of Qingdao University(Engineering & Technology Edition)，2001，16(1)：6-10.

[13]ROBINETTE D，GRIMMER M，BEIKMANN R.Dynamic torque characteristics of the hydrodynamic torque converter [J].SAE International Journal of Passenger Cars-Mechanical Systems，2011，4(2)：1023-1032.

[14]陈东升，项昌乐，刘辉.液力变矩器的动态特性和动力学模型研究 [J].中国机械工程，2002，13(11)：913-916.

CHEN Dong-sheng，XIANG Chang-le，LIU Hui.Study on the dynamic characteristics and dynamics model of hydrodynamic torque converter [J].China Mechanical Engineering，2002，13(11)：913-916.

[15]朱经昌.液力变矩器的设计与计算 [M].北京：国防工业出版社，1991：16-20.

[16]王海燕，卢山.非线性时间序列分析及其应用 [M].北京：科学出版社，1991：16.

s： Supported by the National Major Scientific and Technological Achievements Transformation Project ([2012]258)and the Industry Support Major Item of Fujian Province(201311019)

Transfer Function Representation of Dynamic Circulating Flow Rate of Torque Converter

LIWen-jia1WANGAn-lin1MENGQing-hua1LIXiao-tian1HANJi-bin2

(1. School of Mechanical Engineering，Tongji University，201804，Shanghai，China；2. Shantui Construction Machinery Co.，Ltd.，Jining 272073，Shandong，China)

In order to rapidly solve the dynamic response of circulating flow rate of torque converter，a transfer functions representation method for dynamic circulating flow rate is proposed. In this method，through the derivation on the basis of one-dimension flow theory，a torque converter with certain structure is selected as the research object，and dynamic circulating flow rate is regarded as a first-order linear system’s response with the input of static circulating flow rate. Then，the transfer function of dynamic circulating flow system is constructed according to the static and dynamic CFD (Computational Fluid Dynamics) simulation data under simple working conditions in torque converter’s common working range. Simulated results show that the proposed method helps achieve a fit goodness of 0.987 for dynamic circulating flow rate prediction in common working range，and a fit goodness of 0.95 for input and output shafts’ dynamic torque prediction； and that，in comparison with CFD simulation，the proposed method greatly increases the calculation speed only with a slight decrease in calculation accuracy，so that it is effective in rapidly solving the dynamic response of torque converter.

torque converter； dynamic circulating flow rate； transfer function； computational fluid dynamics simulation； one-dimension flow theory

1000-565X(2016)07-0022-07

2015-11-20

国家重大科技成果转化资助项目(财建[2012]258 号)；福建省产业支撑重大项目(201311019)

李文嘉(1989-)，男，博士生，主要从事液力变矩器定制化设计理论研究和工程机械整机数字化匹配研究.E-mail：pigeon_lwj_1989@126.com

TH 137.332doi： 10.3969/j.issn.1000-565X.2016.07.004