一类源于各向异性板振动模型的四阶非线性椭圆偏微分方程解的存在性

洪军龙， 安玉坤

(南京航空航天大学 理学院，南京 211106)



一类源于各向异性板振动模型的四阶非线性椭圆偏微分方程解的存在性

洪军龙， 安玉坤

(南京航空航天大学 理学院，南京 211106)

研究非线性四阶椭圆边值问题解的存在性.该问题是作为一类刚性纤维编织材料的振动模型而提出的.运用上下解方法证明了上述方程解的存在性.

四阶椭圆方程；非线性；存在性；上下解方法

四阶常微分方程边值问题

是熟知的刻画弹性梁状态的数学模型，在弹性力学和工程物理中有着广泛的应用.因此，非线性四阶微分方程边值问题解的存在性备受众多学者关注，见文献[1-3]等.

马如云在文献[1]中研究了这类边值问题解的存在性，他在关于非线性项的假定条件：

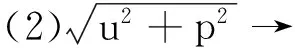
下，根据Krein-Rutman定理和全局分叉理论得到了正解的存在性.

姚庆六在文献[4]中假设：

|f(t,u0,u1,u2,u3)|≤α0(t)|u0|+α1(t)|u1|+α2(t)|u2|+α3(t)|u3|+α4(t)

通过选择适当的函数空间并利用Leray-Schauder非线性抉择对含有2个参数及非线性项f(t,u(t),u′(t),u″(t),u‴(t))含有各阶导数的一类非线性四阶两点边值问题建立了一个存在定理.

同时，也有大量文献研究双调和方程的边值问题

如见文献[5]及其他参考文献.YuanMing Wang在文献[6]中将这类问题推广，研究四阶边值问题

解的存在性.首先，他假设函数f满足条件(H)：

(H)函数f(x,u,v)关于x为Holder连续，存在两个非负的常数γu和γv，γv2≥4γu，使得：

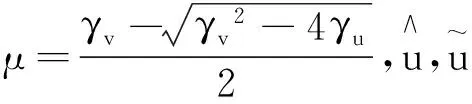
受到这些文献的启发，我们准备在B.kawohl和G.sweers[7]对线性问题uxxxx+uyyyy=f(x,y)研究的基础上,研究非线性边值问题

(1)

解的存在性.其中非线性项f(x,y,u):[0,1]×[0,1]×R→R是连续函数，可以理解为板所受的竖向载荷，与形u有关.

1　预备知识

本节中，主要引述文献[7]中一些在本文中要用到的结果.

引理1(见[7]命题5.4)设f∈L2(Ω)，f(x,y)≥0，则存在一个常数λ0∈(0,2π4)，使得对任意λ∈[λ0,2π4)，问题

(2)

为了证明本文的主要结论，我们还需要借助Leray-Shauder不动点定理.为了完整，也引述如下：

引理3(Leray-Shauder不动点定理)设D是实线性赋范空间中的有界闭凸子集，F:D→D全连续.则F在D上必有不动点.

2　解的存在性

本节中我们研究四阶边值问题(1).设I=[0,1]，Ω=(0,1)×(0,1)，为了方便，将(1)写成

(3)

运用上下解方法证明解的存在性.首先，我们定义方程(3)的上下解.

定义1我们称α(x,y)∈C4[I×I]是(3)的下解，若满足：

αxxxx+αyyyy≤f(x,y,α(x,y)),

α(x,y)|∂Ω=Δα(x,y)|∂Ω=0

若不等号严格成立，则称为严格下解.同理，改变不等号方向，上解的定义也容易给出.

定义2设u,v∈C[I×I],定义u≤v为u(x,y)≤v(x,y)，(x,y)∈I×I，

并且对u≤v，定义连续性区间

[u,v]={w∈C[I×I]:u(x,y)≤w(x,y)≤v(x,y)}.

定理1设f:[0,1]×[0,1]×R→R是连续函数，α(x,y)和β(x,y)分别是(3)的下解和上解，满足α(x,y)≤β(x,y)，并且存在m∈(-2π4,-λ0]，常数λ0∈(0,2π4)，使得对所有(x,y)∈I×I和u∈[α,β]有：

f(x,y,α(x,y))+mα(x,y)≤f(x,y,u(x,y))+mu(x,y)≤f(x,y,β(x,y))+mβ(x,y)

那么，在区间[α,β]中，问题(3)存在一个解.

证明先定义算子Km:C[I×I]→C[I×I]，对每一个h(x,y)∈C[I×I],令Kmh是下述方程的唯一解

定义Nm:C[I×I]→C[I×I]，对每一个h(x,y)∈C[I×I]都有Nmh=f(x,y,h)+mh，其中(x,y)∈I×I.并且，定义Tm:C[I×I]→C[I×I]，Tm=Km·Nm，因此,对每一个h(x,y)∈C[I×I]，函数Tmh是下面方程的唯一解

第一步，证明算子Tm是紧算子.因为f(x,y,u):[0,1]×[0,1]×R→R连续，所以算子Nm:C[I×I]→C[I×I]是连续的.又由引理2，

是有界线性算子.而根据Sobolev嵌入定理，

是紧嵌入.从而

是全连续算子.

第二步，证明Km:C[I×I]→C[I×I]是非减的.令h1,h2∈C[I×I]，h1≤h2，ui=Kmhi，i=1,2.记ω=u2-u1，则

根据引理1可得：ω=u2-u1≥0即u2≥u1.

第三步，证明α≤Tmα，Tmβ≤β.

因为α是下解，那么有

令ω=Tmα-α，则满足如下方程

根据引理1可得：ω=Tmα-α≥0即α≤Tmα.同理可得，Tmβ≤β.

第四步，证明Tm([α,β])⊂[α,β].令u∈[α,β].根据假设：

f(x,y,α(x,y))+mα(x,y)≤f(x,y,u(x,y))+mu(x,y)≤f(x,y,β(x,y))+mβ(x,y)

由第二步，我们得出Tmα≤Tmu≤Tmβ.最后，又根据第三步，我们有Tm([α,β])⊂[α,β].

因为区间[α,β]是Banach空间C[I×I]上的非空有界闭凸子集.由以上四步及引理3，我们得到边值问题(3)至少存在一个解u∈[α,β].

例设λ0如定理1，φ11(x,y)=sin(πx)sin(πy)，

考虑边值问题

(4)

容易验证f(x,y,u)满足定理1中的不等式条件.

代入式(4)左边，得到2π4φ11(x,y).而且φ11(x,y)满足式(4)中的边界条件.所以φ11(x,y)=sin(πx)sin(πy)是问题(4)的严格上解.

从而，问题(4)满足定理1所有的条件，由定理1，问题(4)在区间[0,sin(πx)sin(πy)]内有解.

[1]MA RUYUN,XU JIA.Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem[J].Nonlinear Analysis，2010，72：113-122.

[2]LI YONGXIANG.A monotone iterative technique for solving the bending elastic beam equations[J].Applied Mathematics and Computation， 2010，217： 2200-2208.

[3]MA RUYUN,XU LING.Existence of positive solutions of a nonlinear fourth-order boundary value problem[J].Applied Mathematics Letters，2010，23：537-543.

[4]姚庆六.含有2个参数的非线性四阶边值问题解的一个存在定理[J].云南大学学报(自然科学版),2007,29(6):541-545.

[5]HU SONG,WANG LI.Existence of nontrivial solutions for fourth-order asymptotically linear elliptic equations[J].Nonlinear Analysis，2014：94：120-132.

[6]WANG YUANMING.On fourth-order elliptic boundary value problems with nonmonotone nonlinear function[J].J.Math.Anal.Appl.,2005，307：1-11.

[7]KAWHL B,SWEERS G.On the differential equationuxxxx+uyyyy=ffor an anisotropic stiff material[J].SIAM.J.Math.Anal.,2011，37(6)：1828-1853.

[责任编辑王新奇]

Existence of Solutions for A Class of Four Order NonlinearElliptic Partial Differential Equations Derived Fromthe Vibration Model of Anisotropic Plates

HONG Jun-long,AN Yu-kun

(SchoolofScience,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China)

Inthispaper,westudytheexistenceofsolutionsfornonlinearfourorderellipticboundaryvalueproblem.Theproblemispresentedasakindofvibrationmodelofarigidfiberbraidedmaterial.Weprovetheexistenceofthesolutionsoftheaboveequationsbyusingthemethodofupperandlowersolutions.

fourorderellipticequation;nonlinear;existence;upperandlowersolutionsmethod

1008-5564(2016)03-0010-04

2015-12-20

洪军龙(1990—)，男，安徽马鞍山人，南京航空航天大学理学院硕士研究生，主要从事偏微分方程研究;

安玉坤(1962—)，男，甘肃兰州人，南京航空航天大学理学院教授，主要从事偏微分方程研究.

O175.8

A