牵引电机绝缘系统的温度场分析

刘冠芳， 张　洁， 张山弟， 孟洁瑞

(中车永济电机有限公司， 山西永济 044502)



牵引电机绝缘系统的温度场分析

刘冠芳， 张洁， 张山弟， 孟洁瑞

(中车永济电机有限公司， 山西永济 044502)

建立牵引电机绝缘系统温度场分析的CFD模型，介绍了绝缘材料导热系数测试试样的制作和测试方法，对不同类型的少胶云母带随温度变化的导热系数进行了测试，并使用通用流体计算软件对异步牵引电机绝缘系统的温度场进行了仿真计算，得到了电机整体及绝缘系统的温度场分布图，结果证明定子线圈绝缘层表面温度与线圈内部导线温度差因所处的位置不同而不同，最高温差可到达11℃，这种绝缘系统的温度场分析结果为绝缘结构设计提供了依据。

牵引电机； 温度场； 绝缘系统； 导热系数

电机温升是电机运行的重要指标，直接影响到电机寿命和运行可靠性[1]，温度过高会使整个定子烧毁或使定子绕组绝缘损坏而引起股间短路，造成极大经济损失；相反如果温度过低，会造成铜、铁、绝缘等材料的浪费，增加电机制造成本。因此，计算电机及绝缘系统的热场对电机的设计和运行具有重要的指导意义。

本文建立了适用于牵引电机绝缘系统温度场分析的模型，并对绝缘材料的导热系数进行了测试，通过通用流体计算软件分析得到牵引电机整体及绝缘系统的温度场分布。

1　绝缘材料导热系数测试

导热系数是指在稳态传热条件下，1 m厚的材料两侧表面的温度差为1℃，通过1 m2面积所传递的热量，单位为W/(m·K)。导热系数与材料的组成、结构、密度、含水率、温度等因数有关。电机绝缘系统由多种材料复合而成，其导热系数的确定对于热仿真计算分析的正确性非常重要，需对电机所涉及的绝缘材料进行制样和测试分析。

1.1试样尺寸

测量所需试样须为端面平行而光滑的片状固体材料，内部材质均匀。通过加工将其制备成端面平行光滑的试样。可选形状一般包括圆片与方片，相对而言圆形样品较为标准，水平各方向上边界条件一致，径向热流较均匀，较易修正。

在传热分析中，热扩散系数是热导率与比热和密度的乘积之比。它表示物体在加热或冷却中，温度趋于均匀一致的能力。根据不同的样品材料的热扩散系数选择合适的样品厚度。一般的建议值如下：对于高导热材料，热扩散系数>50 mm2/s(如金属单质、石墨、部分高导热陶瓷等)，建议厚度2～4 mm。对于导热较差材料，热扩散系数在1～50 mm2/s之间(如大部分陶瓷、合金等)，建议厚度1～2 mm。

由于文中所测材料为绝缘材料导热系数较小，因而可以选择厚度较小的试样，所有试样的尺寸大约都在φ12.5 mm×1 mm的圆片状试样。

1.2试样制作

为了更准确的反映绝缘结构的导热系数，测试所有材料浸漆后的导热系数。将不同材料叠成1 mm左右，用层压板夹紧，浸漆后用雕刻机制作成标准试样，这种方法不适用于薄膜。

1.3测试及计算方法

使用热分析仪器DSC和LFA进行对比热和热扩散系数进行测试。

用比热软件对DSC试验所得的数据进行计算和分析，来测定物质的比热。运用公式：

(1)

式中：CP,s(t)为在温度t时的样品比热，J/(kg·K)；CP,std(t)在温度t时的标样比热，J/(kg·K)；Mstd为标样质量；mg；Mstd为样品质量，mg；DSCt(t)为在温度t时样品曲线的DSC信号,UV；DSCstd(t)为在温度t时标样曲线的DSC信号,UV；DSCb1(t)为在温度t时基线的DSC信号,UV。

最后根据公式：导热系数=热扩散系数×比热×密度，计算出导热系数。

1.4测试结果

不同材料浸相同的绝缘漆后的导热系数测试结果如下：

从测试结果可以看出绝缘材料的导热系数是随着温度的变化而变化的，变化范围比较小，不同补强方式的云母带的导热系数不同，随温度的变化趋势也不同。图1和图2中的试样厚度是相同的，可以看出低温时聚酰亚胺薄膜补强的少胶带的导热系数大于聚酯薄膜补强的少胶带，这主要是因为聚酰亚胺薄膜的导热系数高于聚酯薄膜；玻璃布补强的少胶带和双面补强的少胶带的低温导热系数基本相同，高温时双面补强的少胶带导热系数较高。

图1　聚酰亚胺薄膜补强少胶云母带导热系数

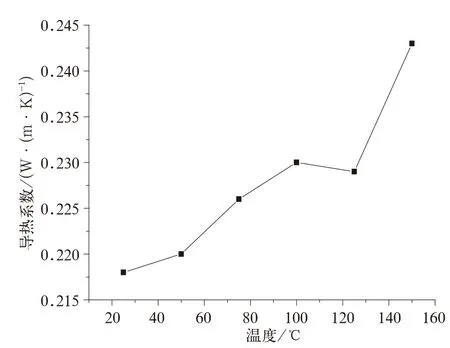
图2　聚酯薄膜补强少胶云母带导热系数

图3　玻璃布补强的少胶云母带的导热系数

图4　薄膜和玻璃布双面补强少胶带导热系数

2　流动换热仿真模型建立

2.1建立三维模型

在分析软件中直接建立几何模型过程比较复杂，操作步骤繁琐，而且有些功能不够全面，因而一般不会在分析软件中直接建立几何模型，而是导入外部的模型。本文计算的电机包括定子铁芯、定子线圈、转子铁芯、转子导条模型。

2.2模型简化

鉴于电机实际几何模型比较复杂，其中又包含许多具有尺寸较小的部件，若按照原始几何模型在流体仿真软件中建立模型，将会耗费巨大的存储和计算资源，因此需要对原始几何模型进行一定的等效简化：

(1)忽略转子导条和铁芯间的接触热阻；

(2)在电机处于稳态，电机转轴忽略不计；

(3)在电机表面散热处理时，为了简化分析，对机壳外轮廓结构做一定的等效简化处理；

(4)忽略轴向热流密度。

2.3建立计算网格

在网格划分时，可以根据需要选择是否需要精细剖分还是粗剖分，对于仿真分析需要深入研究的区域或者流动传热变化剧烈的地方需要细致剖分，而对电机表面等温度变化缓慢的地方则不需要细分，剖分工作的效率取决于计算机硬件系统，剖分越细，做需要离散数据处理越多，因而计算机耗时也就越多[2]。同时网格的处理还需结合电机运行工况、计算模型稳定性、计算精度做相应的调整。对建立好的几何模型划分网格，由于求解区域的复杂性，采用结构化的六面体(Hex)与多面体(Poly)网格相结合的方式。

图5　电机模型网格剖分图

2.4损耗计算

电机是一种机电能量转换装置，在机电能量转换过程中不可避免地要发生机械摩擦，涡流等损耗，从而导致电机发热、温度升高。产生电机损耗的原因根据部位划分主要有以下几种：

(1)铁芯损耗[3]

由于磁场的变化导致铁芯产生涡流，这不仅包括主磁场的变化，也包括谐波磁场在定转子中引起的损耗，其中漏磁也占有一定的比例：

(2)

(3)

其中：

Ph为磁滞损耗,kW；PW为涡流损耗,kW；f为频率MHz；Bm为磁通密度, Wb；V为硅钢片体积,m3；ρ硅钢片电阻率,(Ω·m)；d为硅钢片厚度,m；K为常数。

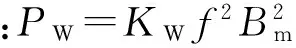
(4)

式中：CFe为铁芯损耗系数，由工程经验决定；G为质量kg。

(2)绕组损耗

处理电流绕组产生的基本损耗，还有电刷和换向器之间的接触损耗与漏磁场和谐波磁场在绕组中产生的铜耗：

(5)

式中I为绕组电流，A；R为绕组电阻，Ω；M为绕组相数。

(3)机械损耗

电机中轴承摩擦，电刷摩擦，转子旋转和气隙流体之间的摩擦属于机械摩擦，在电机损耗中不容忽视。

2.5温度场的建模方程

温度场的建模方程为质量、动量以及能量守恒方程，如下所示：

质量守恒方程：

(6)

动量守恒方程：

(7)

能量守恒方程：

(8)

式中ui为速度；E是总焓；μt湍流黏性系数；Prt湍流普朗特数；T为温度。

2.6材料属性

在计算过程所需要的材料属性如表1所示：

表1　材料属性

3　牵引电机及绝缘系统的热场计算

3.1温度场仿真计算结果

分别取线圈端部、引线以及直线部分的点的仿真计算结果如下：

位于线圈端部的绝缘层的温度低于导线的温度，位于铁芯部分的绝缘层温度高于线圈温度。这是由于：

(1)由于在端部空气冷却绝缘层，热量自导体向外传递；

(2)定子铁芯本身存在损耗而产生温度，该温度高于导线温度，其热量通过绝缘层向导体内部传递；

(3)进口端部温度低于出口端部是由于进口空气温度低于出口部分。

图6　定子线圈温度分布图

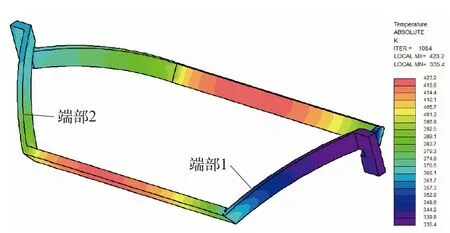
图7　线圈绝缘系统的温度分布图

表2　绝缘系统的温度场分布　℃

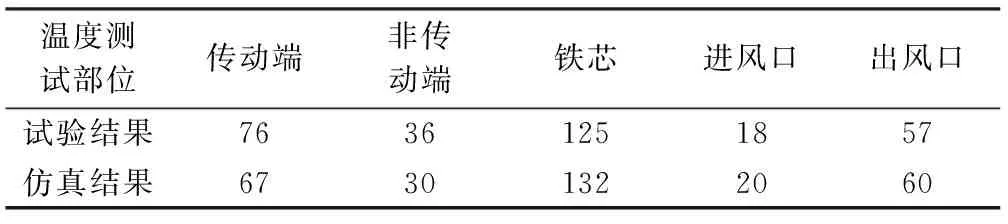
表3　试验数据与仿真结果对比　℃

3.2试验与仿真对比

由于绝缘系统的温度点再试验过程不容易采集，因

此使用其他部分进行对比。

从两组数据可以看出：

(1)在相同通风量条件下，两者的进出口温差基本相同；

(2)传动端与非传动端的试验数据测得的是某一点的数据，而仿真值为这些区域的体积平均值，故存在误差；

(3)铁芯温度试验值低于仿真值，其原因为测试铁芯温度的热电偶为铠装PT100，其与铁芯接触面存在接触热阻引起温差。故铁芯接触面温度要高于测试值；

(4)由于绝缘层导热系数实际上是随温度发生变化的，而仿真为了简化工作量将该值设为常数，所以仿真结果亦存在一定的误差。

4　结束语

本文介绍了绝缘材料导热系数测试试样的制作方法，通过该方法得到了常用绝缘材料的导热系数，同时建立电机绝缘系统温度场分析模型，并对异步牵引电机绝缘系统的温度场进行仿真，结果表明：

(1)导热系数是随着温度变化的，变化范围不大；

(2)定子线圈绝缘层表面温度与线圈内部导线温度差因所处的位置不同而不同，原因是热量传导方向不同；

(3)绝缘系统的温度场分析结果为绝缘结构设计提供了依据，虽然试验结果与仿真结果还存在差异，但通过原因分析，能够指导后续的仿真分析工作。

[1]杨丽伟，张奕黄.异步牵引电机的温度场分布[J].大电机技术,2008, (3):4-7.

[2]张洪亮.永磁同步电机铁芯损耗与暂态温度场研究[D].哈尔滨：哈尔滨工业大学,2010.

[3]马路.感应电机磁场和热场的分析[D].阜新：辽宁工程技术大学,2013.

Analysis on Temperature Field of Traction Motor Insulation System

LIUGuanfang，ZHANGJie，ZHANGShandi，MENGJierui

(CRRC Yongji Electric Co.， Ltd.,Yongji 044502 Shanxi, China)

The CFD model of temperature field analysis of traction motor insulation system is established in this paper. The paper introduced the insulation material coefficient of thermal conductivity test sample production and test methods, and the use of general fluid calculation software for asynchronous traction motor insulation system simulation on temperature field, finally achieved the temperature field distribution of the motor and the insulation system. Results show that the stator coil insulation surface temperature and internal wire coil temperature difference varies because of the position, the highest temperature difference can be reached 11 k, the results of temperature field analysis provide a basis for insulation structure design.

traction motor; temperature field; insulation system; coefficient of thermal conductivity

1008-7842 (2016) 03-0143-04

��)女，工程师(

2015-12-18)

U264.1

Adoi:10.3969/j.issn.1008-7842.2016.03.32