基于品牌信息时效性理论的广告投放密度测算方法实证研究

周云+祝合良

中图分类号：G206 文献标识码：A

内容摘要：精准确定广告投放密度是广告界必须面对的问题，也是品牌界的难题。通过对广告效果的测评和有效到达率的测算，可确定广告的间隔期，以单位时间除以间隔期得到广告投放密度。但受限于广告效果测评的方法，广告投放的间隔期无法精确的测算出来，这也使得企业不能科学确定最低投放密度。以至于在品牌塑造的过程中，传播成本的定量决策缺乏科学依据。本文以品牌信息本论为基础，通过品牌信息时效性的定量研究成果确定品牌信息的衰减速率，并以此测算广告信息的间隔期以及投放密度。最后运用案例试算实证该方法的可行与有效。

关键词：品牌信息 品牌时效性 广告投放密度 广告投放间隔期

引言

广告是创建品牌的主要工具，也是品牌运作的主要成本，“既能够保证品牌的影响力不减，又能够减控广告费用”是运用品牌进行营销的企业着重考虑的管理目标之一。

广告界有句名言，“我知道我的广告费至少浪费了一半以上，但我不知道究竟浪费在哪里”，其意指广告投放不科学而造成巨大浪费的问题。广告实务中对广告投放密度的测算方法过于笼统，一般使用千人成本、到达率等简单计算参数作为依据，做出投放间隔期及投放密度等重要决策，失误频现。归咎原因在于这一过程的依据缺乏对广告效果的科学定量分析，只能凭借决策者的管理经验估计或者是消费者对其反应来判断。

广告效果的定量测评从广告本身进行是行不通的，应当从广告的根本目的入手更为合理，广告的短期目的是销售，长期目的是树立商誉，也就是为品牌而广告。大卫·奥格威（2003）曾做出过“所有广告都应该是为品牌资产增加服务的”的论断，广告短期效果应该以销售额增加率衡量，而长期效果的测评应当从它对品牌的作用进行才是科学的。广告投放密度是广告长期决策的内容，不是为短期销售服务的，因此广告投放密度问题应该从品牌信息量的角度去理解较为合理。“基于品牌信息时效性理论的广告投放密度的测算方法”是对品牌管理理论的发展，也是对广告学理论薄弱领域研究的深入，同时也能够为企业管理人员在进行品牌管理和广告策略的安排起到指导性的作用。本文就是针对这一问题的要害所在，从品牌的定量分析角度，解决科学确定广告投放密度的问题。

本文所研究的命题基于品牌信息的时效性的角度，所以这一命题以两个理论的前期研究结论为基础：其一，是关于“品牌时效性与品牌忠诚度的关系”，品牌忠诚度是可以科学测算的，这一基础理论将品牌忠诚度的测算运用在品牌时效性问题中，使得品牌时效性成为一个可以定量分析的问题；其二，是关于“广告信息与品牌时效性的关系”，这一部分的结论解释了品牌信息与广告信息之间的复杂关系。最终使得在“广告信息确定的情况下维持品牌总信息量不变的间隔期”得以科学确定，由此解决广告投放密度的计算难题。

品牌时效性与品牌忠诚度的关系

Palto ranjan datta（2003）在品牌忠诚度的多维作用研究中发现了品牌忠诚与品牌在消费者心理存在的时间长短有关系，在当时并没有引起学界的重视，“品牌在消费者心理存在的时间长短”其实就是品牌时效性问题，他揭示了品牌忠诚的最本质问题，也为科学测算品牌忠诚度提供了依据。谭勇（2008）运用艾宾浩斯的曲线对品牌传播长期有效性进行了初步研究，并对相关的概念进行了规范。吕海平（2009）所著《品牌信息论》将品牌发生发展和传播的过程归结为品牌信息的传播过程，从信息的角度重新审视了品牌作为经营现象的过程；周云（2008，2014）提出了品牌本质是信息的假设，品牌作为信息存在时效性的问题才开始引起学者们的注意，并发表了《品牌信息本论》，该理论按照Aaker（1991）对品牌资产进行度量的逻辑框架，使用信息度量的基本公式将品牌包含的信息量进行了完整的度量，其过程是按照品牌从知名度、认知度、联想度、美誉度、忠诚度的顺序逐一进行信息量的转换计算，品牌在消费者心理留存时间才真正与品牌忠诚度建立的联系，提出品牌忠诚度的作用是维护品牌时效性。

品牌本质是信息，可以推知品牌和其他类型的信息一样都具备一切信息的属性。信息的基本属性就是“它只和时间有关系，随着时间序列衰减”，这是它的基本属性，品牌作为信息当然也不会背离“只与时间有关系”这一基本规律。因而，对于品牌而言，存在一个确定的衰减率所决定的自然衰减规律，品牌是随着时间自然衰减的。

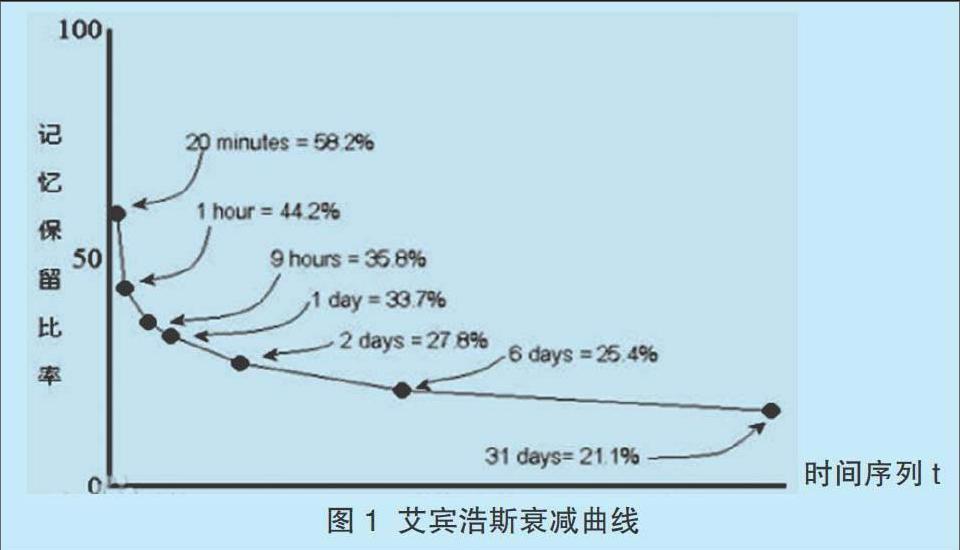
信息的有效是建立在记忆的基础上的，品牌信息对消费者的效用也是建立在消费者的记忆基础上的。如果没有消费者对品牌的记忆，也就没有任何品牌信息。心理学家们对一次记忆在大脑中消失的速度和规律有过完整深入的实证，其中以艾宾浩斯的研究最为著名，是“关于艾宾浩斯记忆曲线的定量研究”，艾宾浩斯在实验室中经过了大量测试后，产生了不同的记忆数据，从而生成的一种曲线，是一个具有共性的群体规律。这就是揭示遗忘规律的艾宾浩斯遗忘曲线，如图1所示，图1中竖轴表示记忆程度，横轴表示时间序列（天数），曲线表示机械学习实验的结果。此记忆曲线并不考虑接受试验个人的个性特点，而是寻求一种处于平衡点的记忆规律。这条曲线说明人的遗忘是有规律的，遗忘的进程很快，并且先快后慢。易非易（1997）基于这一理论解释了信息衰减规律。基于此，品牌信息传递同样符合艾宾浩斯遗忘曲线，但由于每一个品牌的信息量质量不同，消费者偏好不同，则每个品牌的信息衰减的形态不同，但衰减的基本规律都符合艾宾浩斯曲线。

在品牌自然衰减和品牌忠诚度共同作用下，品牌具有了与时间序列的相关性，意指品牌具有了与时间相关的动态性质。一个品牌在不同的时间节点上，它的影响力、价值等都是不同的，这就是品牌时效性。

由上可知，品牌时效性是品牌自然衰减率和品牌忠诚度两个指标所决定的。时效性研究就是针对品牌忠诚度和品牌自然衰减的研究。

品牌忠诚度是一个用于测量品牌时效性的定量指标，其原意是测度品牌对消费者的品牌偏好或消费习惯的影响程度，是一个关系到品牌生存与发展的重要指标，具有一定的品牌忠诚度的品牌会具有抵抗信息自然衰减的效力，同时也就具有了一定程度抵抗风险的能力，使品牌保持时效性就是品牌具有了长久的生命力。简言之，忠诚度的作用就体现在一些消费者的品牌信息能够在忠诚度的作用下不衰减或衰减缓慢，从而使得品牌信息持续有效。

广告投放密度（间隔期）与品牌时效性

广告投放有集中投放和分散投放两种基本形式，二者没有清晰的界限，也没有具体的指标来判断集中和分散。广告投放密度是指厂商在单位时间内播放广告的次数，用来描述广告投放的集中程度，厂商一般以淡旺季为调整广告投放密度的参考依据，广告投入密度是重要的经营策略，对它的定量分析很有必要。

假设：厂商仅仅向消费者发出一则广告（品牌信息）就停止其它的所有品牌（信息）活动，这条广告信息即使完全到达了消费者，也会立刻开始自然衰减，其衰减的趋势符合艾宾浩斯记忆与遗忘规律，就是一条趋于一个较低固定值的曲线，如图1所示。这一规律使得即使是已经获得了很高知名度的品牌也会持续地通过广告等信息活动将品牌信息重复地传递给消费者，目的就是强化消费者对品牌信息的记忆，阻滞或减缓品牌信息的自然衰减，让它长期保持一个相对稳定的状态。

从厂商在一定间隔期后的第二次广告信息达到消费者起，这两次广告信息进行的是一种复杂的叠加活动。其中有初次接触信息的消费者，也有首次接触已经遗忘的消费者第二次接触广告信息，也有首次接触已经记忆的消费者重复接触广告信息。

如图2所示，厂商的一次广告信息量为α，经过间隔期t0后，会按照信息衰减率进行自然衰减β至一定的留存水平（α-β），当第二次广告信息到达消费者时，消费者的记忆留存量大于原有水平，才说明广告信息的重复是有效的传播活动。进行多次重复后，消费者对品牌信息的留存量才能够达到对消费者有影响的水平，此时称广告信息积累成为品牌信息量。

品牌时效性函数与品牌信息衰减率的推导

如果只是接受一次信息，衰减规律是很容易掌握的，但反复信息的留存量的度量要复杂得多。品牌信息的衰减系数与品牌的质量有关，所以在对此系数进行推算需要考虑与品牌质量有关的因素。品牌信息的自然衰减系数除了记忆模型的自然衰减系数之外，与品牌美誉度关系最大。一般而言，美誉度越高，意味着品牌信息越容易被记忆或越不容易被遗忘。

（一）品牌信息衰减率的推导

品牌信息与间隔时间有关，间隔时间越短越容易反复留存，品牌信息一般不会间隔很久，反复程度以及反复内容是否一致等都会对留存信息有影响。多次信息反复叠加就形成了一组多镒记忆的曲线，如图3所示。

图3的纵轴为品牌的信息量或品牌的价值，用于表示该曲线的函数就称为品牌价值函数或品牌信息量函数，这一函数式中包括了对品牌量的基本度量公式，同时也包括品牌时效性函数。

一个由零开始创建的品牌，还没有美誉度，重复率也为零，此时衰减函数是最大值。随着美誉度、忠诚度的形成，平均重复率也逐渐稳定，N（E）函数的图像也逐渐清晰，如下解释通过图像推导品牌信息衰减函数的过程。

令间隔期趋近于零。拟合品牌信息重复信息折线（图3上图）为多镒曲线（图3下图）。品牌信息不再是一则信息沿着一条固定规律的折线，而是一个受到各种因素干扰的多镒记忆衰减曲线，该曲线的斜率就是衰减函数。

多镒曲线是复杂记忆的一种，是一种信息量留存在多重干扰项作用下的复合函数曲线，说明品牌衰减率本身也是一个动态的函数，它反映该品牌的信息质量，拟合优度与维系这个质量的重复率有关。品牌信息的质量是由品牌美誉度决定和单条信息的衰减率决定的，为此品牌多镒曲线的函数表达式为：

y=f[ax，N（x）] （n→+∞，t0→0） （1）

多镒曲线的导数即为品牌信息的衰减率，则：

N（x）=y`=f`[ax，N（x）] （2）

推导N（x）步骤如下：

（3）

（二）品牌时效性函数的推导

品牌时效性反映了品牌具有与时间序列有关的动态特性，一个品牌即使所有因素都不变，在不同时间节点上的品牌价值也是不同的。这一时效性至少由三个要素共同组成，其一是品牌固有的信息衰减率，其二是品牌忠诚度，其三是时间序列。

品牌衰减规律是“品牌本质是信息”的直接体现，品牌忠诚度在品牌价值度量框架中的位置既不是改变品牌信息的量，也不是改变品牌信息的单价，而是品牌信息时效性函数当中。品牌信息自然衰减是随着时间推移而发生的，品牌忠诚对这一信息衰减过程起到阻滞与减缓的作用。

对品牌信息的时效性函数推导是通过品牌衰减规律与品牌忠诚度的关系予以论证和推导的。按照上述变量对品牌的作用和艾宾浩斯衰减函数的结构，构建三者与时效性的关系，建立一个时效性与时间、衰减系数、忠诚度有关的函数。

在品牌价值度量框架里设有一个与时间序列有关的时效性函数TL，取值（0，1]，其中用到了衰减率函数、忠诚度和时间三个参系数，得到：

TL=T[N（x），L，T] （4）

TL趋近于0时，意味着该品牌信息对消费者几乎没有什么影响；TL在（0，1）时，意味着信息按照其固定的衰减率随时间衰减；TL=1时，意味着所有的消费者都是品牌忠诚者，品牌不随时间衰减。

衰减函数的倒数为衰减率，加之时间序列的指数函数为品牌信息的时效性TL，衰减函数与忠诚度的差值是品牌忠诚度起作用后的实际衰减函数，见式（5）：

（5）

其中，TL表示品牌信息的时效性，T代表时间序列或期数，N（x）表示与品牌信息的衰减函数，L表示消费者的忠诚度。

该函数符合艾宾浩斯衰减规律，随着时间的延伸，TL趋近于0，使得品牌信息量趋近信息留存最小的固定值。N（x）是一个决定品牌信息衰减速度的函数，L是阻滞其衰减的作用。二者与时间序列共同构成一个函数，决定了品牌信息的多镒信息曲线规律。

忠诚度越高，N（x）-L的值越小，如N（x）=2、忠诚度100%时，N（x）-L=1，TL=1，即没有衰减。为此，可以预见衰减函数N（x）的最小值应该是2。

基于品牌时效性公式的广告信息间隔期与投放密度测算

假设：某品牌现具有的总信息量为Ω，意指该品牌具有了确定的市场影响力或品牌价值，若不做任何与品牌信息有关的工作，该品牌将按照它固有的衰减率逐渐丧失影响力。内容和传播渠道相同的广告可以视为等量的信息，每一则广告都包含有等量δ的信息量，在传播中无差异。当品牌由自然衰减至由品牌信息的衰减至Ω-δ时，等量的品牌信息传播活动可以使得品牌信息总量恢复至原来Ω的水平，这两次信息之间的时间间隔就是两次等量信息的间隔期。

重复的增加广告最有效的间隔就是当品牌衰减至Ω-δ时，品牌对消费者的影响力恢复原有水平，由品牌确定的Ω、δ可以精确的推算出这一间隔周期t0，t0的最大值是维护品牌影响力（品牌信息量）的最小成本，是品牌信息有效作用的间隔上限，小于Δt的间隔期称为广告的有效间隔期。如要品牌影响力（品牌信息量）增加，就得使投放广告信息的间隔期小于最大间隔期。

由此可以推导出两次等量信息的间隔期：

令某品牌的信息总量在t=0时为Ω；品牌信息传播活动中，每次同样的品牌信息的信息量相等，为固定值δ。

假设：δ不受递减效应的影响。衰减曲线的品牌信息量函数表达式为：

（6）

当Y=Ω-δ时，t的位置即为重复信息的位置，推导过程如下：

整理后，得：

（7）

推导过程示意图如图4所示。

广告投放密度的是单位时间与间隔期的比值，即：

（8）

再由对品牌忠诚度作用和位置的分析，当品牌忠诚度不为零时，衰减曲线发生变化，衰减率变成，品牌信息的衰减变缓，间隔期长度增加。推导过程示意图如图5所示。

由图5可以看出：忠诚度L的出现，降低了品牌信息的衰减率，使得曲线向上移动，在等量信息δ的支持下，t0增加为t0+Δt。增加了的品牌有效期使得广告信息的集中度减小，从而降低了维护品牌的成本。

品牌信息的增加和衰减是多重因素作用、又高度重复发生的信息活动。通过品牌信息衰减曲线和计算公式可以从时间间隔的长度找出品牌量的差异或变化，反之亦然，通过品牌量的变化或差异也可以推算出时间间隔增加的Δt。

（9）

将代入上式后，Δt可表示为公式（10）：

（10）

Δt表示间隔期增量，qi表示样本Ei代表的消费者类型人数，Q表示消费者总人数，d%表示知名度，Fi表示E1样本中，符合品牌忠诚者条件的消费者人数，N（x）表示与品牌信息的衰减函数，Ω表示某品牌现具有的总信息量，δ表示每一则品牌信息（广告）包含的等量信息。

（11）

（12）

实证检验

以深圳魅力曲线内衣有限公司的品牌“魅力曲线”的数据，对该公司的广告策略进行调整。

（一）“魅力曲线”品牌的基础数据

通过在深圳的样本调研，获得了2015年3月“魅力曲线”品牌的基础数据，包括知名度、认知度、美誉度和忠诚度，整理数据如表1所示。

（二）间隔期及投放密度的计算

经过测算，2015年3月的“魅力曲线”品牌的确定参数如下：

在深圳的消费者总人数为10357900人；符合品牌忠诚者条件的消费者人数为377331；知名度为20.53%；品牌信息的衰减函数值为1.822；时效性函数值为（0.5587）T；品牌具有的总信息量为338.187806比特；一则电视广告平均受众为77535人；广告每一则品牌信息（广告）包含的平均等量信息为5715比特。

得出：单位时间为一天的实际间隔期计算为2.2小时，而最大间隔期计算应该为9.32小时。

实际广告投入密度为：10.9次/日，最小密度为：2.575次/日。

（三）广告投放密度分析及建议

运算结果确定“魅力曲线”品牌在单位时间为一天的最大间隔期是9.32小时，单位时间为一天的广告投放密度为2.575次/日，在实际经营中，魅力曲线公司每天的投放平均密度高达11次/日，远远高于最小密度，而对比2015年3月与2015年4月一个月的基础数据变化，信息总量的变化并不明显，较高的投放频次使得品牌的有效到达率很高，但边际效应降低得非常明显，建议企业调整广告投放密度为3次/日，在维系品牌信息不衰减或略有增加的情况下，减少广告成本至最小值。

（四）实施效果及评价

“魅力曲线”品牌运营商在2015年5月调整投放密度为5次/日，实施一个月后，2015年6月在深圳再进行样本调研，结果如表2所示。

与2015年3月未调整前的基础数据比较，知名度和美誉度都有一定的增加，忠诚度和认知度略有下降，说明知晓该品牌的消费者数目继续增加，而广告的减少确实使得消费者对该品牌的认知程度下降，美誉度提高是由于使用该品牌产品的消费者增加，同时对该品牌的自传播数目增加，只是有一部分消费者没有形成消费偏好，未能使得品牌忠诚者数目随美誉度增加而增加。

但该品牌的信息总量不但没有下降，还略有增加，说明本次广告投放密度的下降并没有使得品牌的综合影响力下降，总体看，广告调整策略降低了55.04%的广告费用，并没有使得广告效果下降。

结论

品牌时效性是品牌价值动态性的反映，是品牌管理的难点。通过对品牌信息衰退机理的研究，掌握品牌时效性的规律，可以精确计算广告投放的间隔期，从而解决“投放密度难以科学确定”这一广告实务的难题。

本研究的结论可以应用于企业经营决策的定量分析环节，能够在品牌管理方面大幅提高企业管理的科学决策水平，如可以精确地计算出企业知名度发生变化时，精确调整广告投放的次数、频度，甚至投放时机和渠道等决策，为科学运营品牌提供可靠的理论依据。

参考文献：

1.大卫·奥格威.一个广告人的自白[M].中国物价出版社，2003

2.Palto ranjan.The Determinants of Brand Loyalty [J].Journal of American Academy of Business，Cambridge，Hollywood，2003（9）

3.谭勇.品牌传播长期有效性探析—基于艾宾浩斯遗忘曲线和品牌核心价值[J].企业经济，2008（6）

4.吕海平，马瑞，张建生，张倩.品牌信息论[M].吉林大学出版社，2009

5.周云.品牌信息本论—品牌信息本质的确定及其量的度量理论[M].机械工业出版社，2014

6.David A.Aaker，Managing Brand Equity：Capitalizing on the value of a brand name，New York：The Free Press，1991

7.易非易，任力峰，谢嘉平.学习与记忆模型研究[J].数理医药学杂志，1997（2）

8.游士兵，黄静，熊巍.品牌关系中消费者心理契约的感知与测度[J].经济管理，2007（11）

9.王兴元，孙国翠.品牌忠诚度测度及策略导向模型[J].经济管理，2005（1）

10.金立印.员工品牌认同感对内部满意度及顾客服务活动的影响[J].经济管理，2005（4）