框架结构有限元模型的坐标变换方法

罗　帅　刘　伟

(1.绍兴文理学院　土木工程学院,浙江　绍兴312000；2.广东交通职业技术学院,广东　广州510650)



框架结构有限元模型的坐标变换方法

罗帅1刘伟2

(1.绍兴文理学院土木工程学院,浙江绍兴312000；2.广东交通职业技术学院,广东广州510650)

针对框架结构有限元分析过程中的坐标转换关系问题，基于三角函数和应变能关系推导了二维坐标系中框架单元局部刚度矩阵和整体刚度矩阵之间的转换关系，利用功能原理推导荷载向量的局部坐标和整体坐标转换方法，利用所推导的转换矩阵，根据已知的框架结构局部刚度矩阵变换得到整体刚度矩阵.与常用的基于几何投影关系推导出来的单元坐标转换公式相比，新方法具有推导过程逻辑严谨，物理意义明确等优点，算例分析结果表明该方法适合编程应用.

框架结构；有限元模型；坐标变换矩阵；局部刚度矩阵；整体刚度矩阵

0　引言

框架结构在我国是应用较多的结构形式.框架结构又称构架式结构，是由梁、板、柱构成的承重体系：楼板搭在梁上，梁支撑在两边的柱子上，由此把荷载传递给柱子，最后沿着柱子在高度方向传给结构基础.房屋的框架按所用材料分为钢筋混凝土框架、木框架、钢框架等，其中最常见的是钢筋混凝土框架和钢框架，钢筋混凝土框架主要应用于学校、住宅、办公楼等；钢框架则多用于机场、火车站、停车场、体育馆等一些有特殊用途的建筑结构中.

目前框架结构的力学分析主要利用有限元方法进行[1]，有限元方法分析框架结构的基本原理是利用局部坐标系下各种规则的基本单元来模拟实体结构中遇到的各种复杂几何形状[2].进行二维或三维结构分析过程中，在局部坐标系下建立单元的刚度矩阵后，随后的重要步骤就是通过局部坐标与整体坐标之间的映射关系组装整体坐标系下的结构刚度矩阵[3].已有的文献中通常都是直接给出结构整体矩阵和单元矩阵之间的变换关系[4]，这给基本方法的准确应用带来了理解上的障碍，容易造成分析错误.

本文针对有限元模型中整体矩阵和局部矩阵之间的相互关系进行研究，以几何关系及功能原理为分析基础，推导了二维坐标系下两者之间的转换关系，建立了新的坐标变换方法，所得结果对采用有限元方法进行框架结构的设计分析具有指导意义.

1　坐标转换方法

1.1抗弯刚度矩阵坐标对应关系

如图1所示框架结构杆件单元由两个节点组成，每节点具有二自由度，即竖向位移和转角，不妨以变形之前的局部单元起点a(设此节点在整体坐标系中的节点编号为i)为原点，与终点b(在整体坐标系中的节点编号为j)的连线为坐标轴x,垂直于连线方向的坐标轴为y轴，建立框架构件单元的局部坐标系.为方便起见，建议在整体坐标系中结构构件各单元的起始编号小于构件的终点编号.

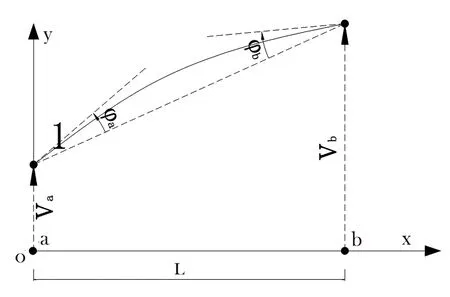
图1　局部坐标系下单元节点位移

这里只考虑了弯曲，因此单元变形在局部坐标系中表现为节点沿竖向坐标轴上的位移和绕节点本身的转角，在局部坐标系中将外力作用下的单元节点位移矢量记为d，节点的位移在局部坐标系中可表示为：

(1)

式(1)中，va，vb分别为点a，点b的竖向位移，φa，φb分别为单元在点a，点b处的转角，本文中矢量上标T表示的是向量或者矩阵的转置(下同).

如图2所示，按右手螺旋定则确定此框架构件单元在整体坐标系下的倾角为θ，则单元的方向余弦符合以下关系：

(2)

式(2)中X,Y是单元节点在整体坐标系中的位置坐标值，下标为其节点编号,L是单元长度：

(3)

将单元节点位移在整体坐标系中记为矢量Dij，则节点在整体系下的位移为：

(4)

式(4)中U，V为整体坐标系中节点i和节点j的位移在两个坐标轴上的投影，不妨规定位移的方向与坐标轴正方向相一致取正号，反之则取负号，Φi，Φj分别为构件在点a，点b处的转角.

图2　整体坐标系下单元的节点位移

由图2可知，构件的变形在局部坐标系和整体坐标系中保持一致，因此有：

(5)

此外有如下三角函数关系恒成立：

cos2θ+sin2θ=1

(6)

利用三角函数代数关系式(6)可将局部位移关系式(1)重写为如下形式：

(7)

以代数的形式将整体坐标和局部坐标之间的对应关系式(5)代入到三角函数关系式(7)中(这一步为本文关键)，化简后可得：

(8)

进一步将关系式(8)用矩阵的形式表示为：

(9)

根据式(9)可以将整体位移和局部位移间的对应关系矩阵S表示为：

(10)

此时可得变换关系：

d=SDij

(11)

假设框架单元构件弹性模量为E，截面惯性矩为I，单元的长度为L，若已知该单元的局部刚度矩阵(是一个对称矩阵)如下[5]：

(12)

则该单元的弹性应变能(标量形式)在局部坐标系中可写成内积形式：

(13)

此时该单元的弹性应变能在整体坐标系中还可以写成内积形式为：

(14)

将式(12)代入到式(13)中，化简可得：

(15)

综合式(13),(14)和(15)可得：

K=STkS

(16)

式(16)即为本文所推导的框架结构有限元模型的整体坐标和局部坐标转换公式，进一步将式(2)和式(10)代入到式(16)中可推导出框架单元在整体坐标系下的刚度矩阵：

(17)

1.2考虑轴向刚度的坐标转换关系

在上述推导过程中仅考虑了单元的弯曲，即刚度矩阵仅考虑了竖向位移和转角，为了更合理地表示每个节点自由度对单元矩阵的贡献，本文拟以上述推导为基础将轴向荷载作用下构件的刚度矩阵和考虑弯曲的刚度矩阵联合起来以建立更符合实际情况的坐标变化方法.已知考虑轴向变形的框架单元在局部坐标系下的刚度矩阵为[4]：

(18)

式(18)与式(12)相似，不同之处在于考虑了构件轴向刚度的影响，由于同时考虑了框架单元的轴向变形和弯曲，此时构件的变形在局部坐标系下表现为节点沿坐标轴轴向和垂直方向的位移及绕节点的转角，将外力作用下的节点位移矢量在局部坐标系中表示为dn，此时在局部坐标系中，单元节点的局部位移为：

(19)

式(19)中ua，ub分别为点a，点b的竖向位移量，中va，vb分别为点a，点b处的竖向位移量，φa，φb分别为构件绕点a和点b的转角.此时节点位移矢量在整体坐标系下的表达式同式(4)，单元在整体坐标系下的倾角的方向余弦表达式同式(2).

根据叠加原理，可以将整体坐标系下节点的位移表示为单元节点沿竖向坐标轴的位移和转角与单元轴向变形之和：

(20)

式(20)与式(5)相比，叠加了节点沿单元轴向位移的部分，化简可得：

(21)

对投影矩阵求逆，进一步整理可得：

(22)

根据式(22)可得整体位移和局部位移间的变换关系矩阵Sn为：

(23)

式(23)与式(10)相似，此时由式(22)可得变换关系：

dn=SnDij

(24)

将单元的弹性应变能在局部坐标系下表示成内积形式：

(25)

则该单元的弹性应变能在整体坐标系下表示成内积形式如下：

(26)

将式(24)代入式(25)中，化简得：

(27)

综合式(25),(26),(27)得：

(28)

式(28)即为考虑轴向变形的框架结构单元刚度矩阵的整体坐标和局部坐标转换方程，进一步将式(18)和式(23)代入到式(28)中推导出整体坐标系下的框架结构单元刚度矩阵如下：

(29)

尽管建立的整体坐标系下的刚度矩阵表达式(29)形式复杂，但是其中的局部坐标和整体坐标变换方程式(23)简单合理，单元刚度矩阵的局部坐标和整体坐标转换方程式(28)便于理解，适合编程实现.

1.3二维荷载向量转换关系

将节点的荷载向量在局部坐标系下表示为fn，则外力作功在局部坐标系中的内积形式为：

(30)

由功能原理表达式Wn=Pn，式(30)中对位移求导可得局部坐标系中节点处力的平衡方程：

kndn=fn

(31)

将节点的荷载向量在整体坐标系下表示为Fn，则与其对应的外力作功在整体坐标系中写成内积的形式为：

(32)

由功能原理表达式Wn=Pn，将式(32)对位移矢量求导可得局部坐标系中单元节点处力的平衡方程如下：

KnDij=Fn

(33)

将式(24)代入式(30)中化简得：

(34)

综合式(24),(30),(34)得框架单元荷载向量的对应关系：

(35)

式(35)即为本文所推导的框架结构单元荷载向量的整体坐标和局部坐标转换关系式.根据式(33)可知整体坐标系中的节点处力的平衡方程：

(36)

式(36)即为本文建立的整体坐标系下框架结构有限元模型力平衡方程.

由于单元的刚度矩阵和荷载向量是有限元建模中的重要环节，因此其推导过程对应用有限元方法求得正确分析结果非常重要.

2　算例分析

如图3所示考虑轴向变形平面刚架[6]，其所受到的外荷载已经在图中标出，已知各杆件材料属性为：EI=2.16×105KN·m2，EA=7.2×106KN，试求节点位移及支座反力.

图3　结构示意及位移编码

第一步，根据式(18)推导单元刚度矩阵，对于单元①：单元长度L=5m，可得单元①的单元刚度矩阵：

(36)

对于单元③：单元长度L=4m，根据已知条件代入式(18)，可得单元③的单元刚度矩阵：

(37)

第二步，推导坐标转换矩阵，根据式(2)求解单元在整体坐标系下的倾角，对于单元①：cosθ1=0.6，sinθ1=0.8(θ1=53.13°)；单元②整体坐标与局部坐标重合，不用进行坐标变换；单元③：cosθ3=0，sinθ3=1(θ3=90°)；根据式(23)得到单元①的变换矩阵为：

(38)

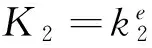
单元③的变换矩阵为：

(39)

将式(37)和式(39)代入式(28)中求得整体坐标系下单元单元③的刚度矩阵K3.至此，本文通过所推导的框架结构有限元模型的坐标变换方法建立了算例的整体坐标下各单元的刚度矩阵.

第三步，单元组合，将求得的单元刚度矩阵K1，K2和K3组合形成整体刚度矩阵，由于算例结构形式简单，这里不妨使用Boole连通矩阵[7]或者更为简便的对号入座法[8]来构造结构整体刚度矩阵KG，由于没有施加边界条件，此矩阵是一个12阶的对称奇异矩阵.

第四步，应用边界条件，由于节点1和节点2是固定的，即在这些点上的节点位移和转角为0，将这些支承条件应用到建立的整体刚度矩阵KG中，得到修改后的整体刚度矩阵K如下：

图4　算例节点位移

(40)

第六步，施加荷载并建立结构刚度方程，由于荷载均施加在单元②上，单元②整体坐标与局部坐标重合，不需要应用式(36)进行坐标变换，因此由图3直接可得：

(41)

由单元②的等效节点荷载可得：

fE=

[0 -45KN -47.5KN·m 0 -45KN 37.5KN·m]T

(42)

从而求出节点荷载向量为：

f=fd+fE

(43)

由此建立结构刚度方程为：

KD=f

(44)

第七步，求解结构刚度方程得到节点3和4的变形向量为：

(45)

由式(45)得框架结构的节点位移如图4所示：

第八步，求解结构支座反力，由变形向量表达式得到总的位移向量DG，支座反力可以从下列方程求出：

R=KGDG-FG

(43)

具体的表达式如下：

(44)

利用所得到的节点位移还可以进一步分析框架单元的内力和正应力，且在计算过程中单元的整体位移和局部位移依然要通过坐标变换矩阵联系起来，由于本文主要讨论有限元建模过程中的坐标变换方法，这里不再赘述.

4　结论

本文围绕框架结构有限元分析中的建模问题，推导了框架单元局部刚度矩阵和整体刚度矩阵之间的转换方法，结果表明：

1)利用三角恒等式和叠加原理推导的考虑轴向变形的框架单元的整体刚度矩阵合理且可行；

2)运用功能原理建立的荷载向量的局部坐标和整体坐标转换方程式物理意义明确，便于理解；

3)新的框架结构刚度矩阵模型变换方法简便快捷，适合编程实现.

[1]J N REDDY. An Introduction to the Finite Element Method [M].2nd ed, New York：McGraw-Hill， 1993.

[2]K J BATHE. Finite Element Procedures[M].Englewood Cliffs, NJ：Prentice Hall，1996.

[3]罗帅, 颜全胜. 桁架结构有限元模型的坐标转换方法[J]. 四川建筑科学研究. 2015, 41(3): 10-13.

[4]R D COOK, D S MALKUS,M E PLESHA, et al. Concepts and Applications of Finite Element Analysis [M]. 4th ed.New York：John Wiley & Sons, Inc., 2002: 61-63.

[5]S MOAVENI. Finite Element Analysis - Theory and Application with ANSYS [M]. 2nd ed. Upper Saddle River, NJ：Prentice-Hall, 2002.

[6]王焕定，陈少峰，边文凤.有限单元法基础及MATLAB编程[M].北京：高等教育出版社，2012.

[7]A P BORESI, K P CHONG, S SAIGAL,Approximate solution methods in engineering mechanics [M]. 2nd ed. New York: John Wiley & Sons, Inc., 2003.

[8]朱慈勉，吴宇清，计算结构力学[M].北京：科学出版社，2012.

(责任编辑王海雷)

Coordinate Transformation Method of Finite Element Model for Frame Structures

Luo Shuai1Liu Wei2

(1. School of Civil Engineering, Shaoxing University, Shaoxing, Zhejiang 312000;2. Guangdong Communication Polytechnic, Guangzhou, Guangdong 510650)

Coordinate transformation is an important step in frame structure analysis using Finite Element Method (FEM). In this study, the transformation matrix was deduced by the relationship of trigonometric functions and strain energy, and the load vector was transformed by work-energy theorem. The element stiffness matrices for frame structure were calculated in local coordinate systems and then transformed into global coordinate systems with the new method. Compared with the general derivation method, the new coordinate method results in rigorous logic reasoning and clear physical significance, and it is simple for comprehension and calculation. The example analysis shows that the method is suitable for computer programming.

frame structure model; finite element method; transformation matrix of coordinates; local stiffness matrix; global stiffness matrix

2016-04-15

广东省自然科学基金资助项目(编号：2015A030310168)，绍兴文理学院科研项目(编号：20155028).

罗帅(1981-),男,湖北天门人,助理研究员，博士，主要从事土木工程结构动力学分析及振动控制研究工作.

10.16169/j.issn.1008-293x.k.2016.08.04

O302;TU12

A

1008-293X(2016)08-0017-07