考虑自重影响的等强度梁弯曲正应力及挠度误差分析

吴瑞潜　邵晓蓉

(绍兴文理学院　土木工程学院，浙江　绍兴312000)



考虑自重影响的等强度梁弯曲正应力及挠度误差分析

吴瑞潜邵晓蓉

(绍兴文理学院土木工程学院，浙江绍兴312000)

利用材料力学方法推导出考虑自重影响的等强度梁弯曲正应力及挠度的精确解，得到忽略梁自重引起的设计误差.研究等强度梁应力及挠度的误差问题，通过算例分析误差的影响因素及其变化规律.结果表明，最大弯曲正应力及挠度的绝对误差均与荷载大小无关，但与横截面位置有关；两者的相对误差与荷载大小与横截面位置有关，但变化规律不同.

等强度梁；弯曲正应力；挠度；误差

等强度梁，即满足梁各个横截面上的最大正应力都相等，并达到材料的许用应力.为保证等强度，设计时通常忽略重力影响，考虑梁横截面抗弯刚度沿梁轴线变化，抗弯刚度沿空间位置而变化的梁通常称为变刚度梁.梁刚度变化包括两个方面，一是截面几何参数的变化，即横截面大小、形状变化，通常指变截面梁；二是材料参数的变化，如功能梯度材料、纤维增强复合材料等非均质材料制成的梁.

梁的等强度设计是一种体积最小、满足强度条件的最优化设计，它广泛应用于土木、建筑等领域，在工程实际中具有重要的意义[1-3].等强度悬臂梁是力学实验中常用的教学设备，在静动态测试中应用比较广泛.静态实验如电阻应变片灵敏系数测定、应变组桥实验等，动态实验如动特性与动应力综合性实验、冲击动应力动荷系数及固有频率测试实验[4-6].变截面梁相关弹塑性分析方面，目前已有不少研究成果.比如李学军等人[7]建立了一种适用于轴向变刚度超静定梁弹性分析的通用力学模型；仲政等人[8]假定功能梯度材料的弹性模量沿梁截面高度梯度变化，提出了等截面梁弹性分析的解析解；张靖华等人[9]考虑梁横截面尺寸和材料参数沿长度梯度变化，应用微分求积法分析了变截面功能梯度梁的弹性弯曲；聂国隽等人[10]假定矩形截面梁的材料为非均匀的各向同性的理想弹塑性材料，在小变形前提下研究了轴向变刚度梁的弹性及弹塑性弯曲问题，导出了截面高度及材料的弹性模量沿梁长度方向按照特殊函数变化时梁弹性及弹塑性变形的解析解.

在计算等强度悬臂梁弯曲正应力和挠度时，忽略梁的自重，即把梁近似看成等高度、变宽度、无重量的悬臂梁，这样的计算结果与考虑自重时一定会有误差.本文考虑梁是均匀、连续并有自重：重度为一定值，并且处处相同.利用材料力学方法推导出考虑自重影响的等强度梁弯曲正应力及挠度的精确解，并与忽略自重影响的情况进行了对比.

1　问题的描述

1.1基本假设

考虑一矩形截面变刚度悬臂梁，形状、几何尺寸如图1所示.梁截面高度为h，宽度沿梁轴线方向线性关系变化，可用式(1)表示.梁的材料为均匀、密实、各向同性的理想弹性材料，拉伸与压缩具有相同的性能，且不考虑剪切对变形及屈服的影响.在变形过程中梁符合平截面假定和小挠度假定.考虑自重时等强度梁所受荷载图如图2所示.

bx/x=b/L

(1)

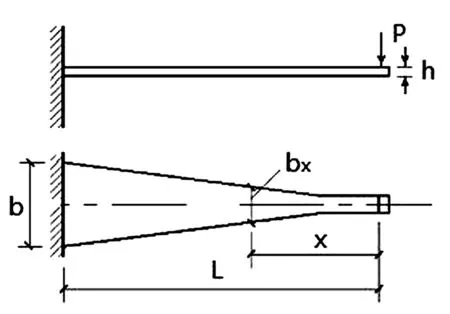
图1　等强度梁几何尺寸示意图

图2　考虑自重时等强度梁所受荷载图

图中,符号意义如下，其中q(x)、q的表达式分别为式(2)和式(3).

P为等强度梁上施加的荷载；L为等强度梁的总长度；b为等强度梁固定端的宽度；h为等强度梁的平均厚度；x为指定截面或百分表测点截面到加载点的距离；bx为等强度梁在位置x处的宽度；q(x)为对应于x距离截面处荷载分布函数；q为固定端截面处荷载分布函数.

(2)

q=γbh

(3)

式中，γ为等强度梁钢材的重度.

1.2基本方程

对于等强度悬臂梁，受竖向荷载(集中力、分布力)时，梁上侧受拉，最大弯曲正应力σmax位于横截面上边缘，为拉应力，根据材料力学理论，可用下式计算：

(4)

当变刚度梁处于弹性变形状态时，梁上任一点的挠度可用挠曲线近似微分方程表示：

EI(x)w″(x)=-M(x)

(5)

2　问题的求解

利用基本方程式(4)和式(5)，以及相关条件，可得到考虑自重时等强度梁最大弯曲正应力及挠度解析表达式，以下是简单的推导过程.

2.1最大弯曲正应力

将弯曲截面系数及弯矩方程代入式(4)，可得梁截面上最大弯曲正应力表达式：

(6)

当忽略自重时，即取γ=0，此时梁截面上最大弯曲正应力为：

(7)

上式即为等强度梁上任一点最大弯曲正应力的近似理论计算值，它与加载值大小有关，但与梁横截面位置x无关.

2.2挠度

将惯性矩及弯矩方程代入挠曲线近似微分方程，即式(5)，并利用式(2)，化简可得

(8)

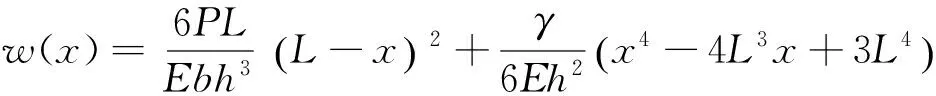
(9)

当忽略自重时，即取γ=0，此时挠度为：

(10)

上式即为等强度梁上任意横截面的挠度的近似理论计算值，它与加载值及梁横截面位置x有关.

3　算例分析

根据上述弯曲正应力、挠度的精确解，可与忽略自重影响的近似解进行相关误差分析等比较.考虑实验室等强度梁的相关参数如下：L=300 mm，b=46 mm，h=3.2 mm，E=2.06×105MPa，此外，梁的材料为钢材，取钢材密度为7.85g/cm3，则其重度为γ=76.93kN/m3.

比较式(6)及式(7)，可得最大弯曲正应力绝对误差：

(11)

显然，绝对误差与横截面位置x有关(γ、h为定值)，而与荷载大小无关.

同样，比较式(9)及式(10)，可得挠度绝对误差：

(12)

显然，绝对误差与横截面位置x有关(γ、E、h、L为定值)，而与荷载大小无关.

根据上述算例，可画出以下图线：弯曲正应力绝对误差-位置曲线(图3)；荷载-弯曲正应力-相对误差曲线(图4)；应力相对误差-位置曲线(图5)；挠度绝对误差-位置曲线(图6)；荷载-挠度相对误差曲线(图7)；挠度相对误差-位置曲线(图8).

对于弯曲正应力，由图3看出，随横截面位置x增大，绝对误差呈抛物线变化，并逐渐增大，在固定端x=300 mm处，绝对误差值最大，但不超过2.5 MPa.对于图4、图5，相对误差随着横截面位置x的增大而增大，但一般不会超过11%；施加的荷载越大，相对误差减小.一般实验选取横截面位置x不超过200 mm，绝对误差值不大于1 MPa，相对误差一般不超过5%，完全可以满足工程及实验室的精度要求，因此可以说是名副其实的“等强度”悬臂梁.

对于挠度，由图6可知，随横截面位置x增大，绝对误差呈非线性减小，在x=300 mm处即固定端，绝对误差为零；由图7、图8可知，随着横截面位置x增大，相对误差也增大，但不会超过10%，荷载越小相对误差越大，荷载越大，相对误差较小并且变化不大.与弯曲正应力相比，相对误差值略大一些，表明横截面位置x的变化对挠度影响要大于弯曲正应力.当处于一般检测位置即x不超过200 mm时，相对误差在10%以内，一般可以满足精度要求.

总之，对于一般检测位置，弯曲正应力的相对误差一般在5%左右或以内，而对于挠度还要考虑荷载不是太小，那么挠度的相对误差也可变得很小.因此，一般情况下，弯曲正应力及挠度均认为可满足工程及实验室的精度要求.

图3　应力绝对误差与位置曲线

图4　荷载-应力相对误差曲线

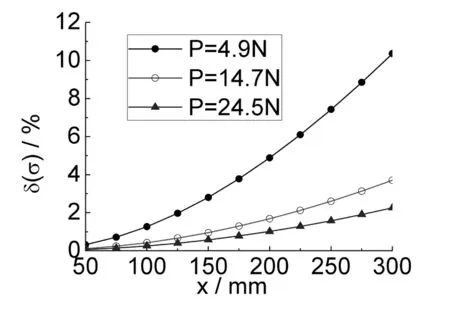
图5　应力相对误差与位置曲线

图6　挠度绝对误差与位置曲线

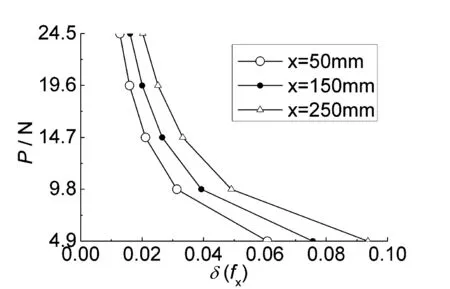
图7　荷载-挠度相对误差曲线

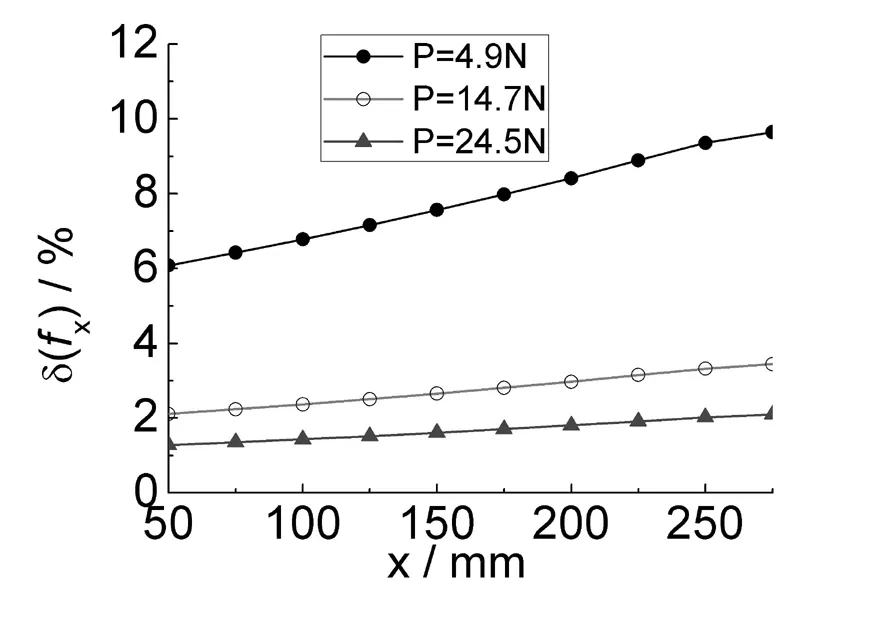
图8　挠度相对误差与位置曲线

4　结论

(1)利用材料力学方法推导出考虑自重影响的等强度梁弯曲正应力及挠度的精确解，显示了忽略梁自重引起的设计误差，为忽略梁自重的设计方法提供了理论依据.

(2)最大弯曲正应力的绝对误差与荷载大小无关，但与横截面位置x有关，并随x增大而增大；当横截面位置x一定时，相对误差随荷载增大而减小.

(3)当等强度梁重度、弹性模量、梁高一定时，挠度的绝对误差与荷载大小无关，但与横截面位置x有关并随x增大而减小.

(4)对于一般检测位置，弯曲正应力及挠度的误差一般在5%左右或以内，可满足实验及工程精度要求.

[1]吴莹,俞焕然,邢静忠.单铰柔韧性机器人手臂的体积优化[J].兰州理工大学学报,1998(3):39-43.

[2]张爱国，陈忠会，马书尧．用边界元法进行等强度梁的形状优化[J]．河北工业大学学报，1997(1):76-81．

[3]李清禄.基于神经网络等强度超静定梁的优化设计[J].甘肃科学学报,2005,17(3):16-19.

[4]姚恩涛，胡明敏．应用《理论力学》与《材料力学》知识的实验方案[J]．实验室研究与探索，2003，22(2)：13-14．

[5]郭迎福，刘权，张越雷，等．基于声卡和LabVIEW的等强度悬臂梁固有频率测试[J]．实验室研究与探索，2009，28(11)：36-38．

[6]邱艳宇，赵跃堂，张虹.等强度悬臂梁自振频率计算与实验研究[J].实验科学与技术，2014，12(2)：26-28.

[7]李学军，朱萍玉，刘义伦．复杂载荷下变刚度静不定梁程序化求解[J]．工程力学，2003，20(4)：116-121.

[8]仲政，于涛．功能梯度悬臂梁弯曲问题的解析解[J]．同济大学学报(自然科学版)，2006，34(4)：443-447.

[9]张靖华，龚云，李世荣．微分求积法求解变截面功能梯度梁的弯曲问题[J]．甘肃科学学报，2010，22(1)：14-17.

[10]聂国隽，徐敏，仲政.轴向变刚度矩形截面梁的弹性及弹塑性弯曲[J].中国科学(物理学力学天文学)，2011(1):86-93.

(责任编辑王海雷)

Error Analysis of Bending Normal Stress and Deflection in Equal Strength Beam with Beam Weight Considered

Wu RuiqianShao Xiaorong

(School of Civil Engineering, Shaoxing University, Shaoxing, Zhejiang 312000)

The mechanics of materials method is applied to derive the accurate solutions to bending normal stress and deflection of equal strength beam considering its weight. The solutions show that the design error is caused by ignoring the weight of the beam. Such error problems as bending normal stress and deflection of equal strength beam were studied. The affecting factors and the variation law of the error were analyzed via an example. The results show that absolute errors of maximum bending normal stress and deflection are independent of the load size, but are related to the position of cross section. Their relative error is associated with the load size and the position of cross section, but with a different variation law.

equal strength beam; bending normal stress; deflection; error

2016-04-16

国家青年基金项目(编号：41202222)

吴瑞潜(1972-)，男，安徽潜山人，博士，讲师，主要研究方向：土力学及地基处理.

10.16169/j.issn.1008-293x.k.2016.08.02

TU311.4;TU323.3

A

1008-293X(2016)08-0009-04