基于领导跟随的船舶航迹控制

齐小伟 任 光

（大连海事大学 轮机工程学院 大连116026）

基于领导跟随的船舶航迹控制

齐小伟 任 光

（大连海事大学 轮机工程学院 大连116026）

无人艇协同编队控制具有重要的军事和商船应用前景。利用多智能体聚集模型，基于leader-follower的目标跟踪，实现了含有模型不确定性与未知海浪流干扰项的多无人艇协同编队控制。采用单隐层神经网络逼近船舶整体未知项和环境干扰，引入一阶滤波器代替反步计算中的微分项，显著减少了计算量。利用时-空解耦方法，各船舶通过交互航迹参数信息，间接实现分散协同编队控制。利用Lyapunov稳定性分析方法，证明闭环系统所有状态和信号收敛于一有界集。通过选择合适参数，可使控制精度误差范围为任意小，仿真结果验证了控制算法的有效性。

无人艇；神经网络；不确定性；多智能体；一阶滤波器；编队控制

引言

近几十年来，随着海洋的快速开发，各国在海洋经济和军事活动日益频繁，使船舶编队控制成为船舶运动研究中的热点问题。多船编队相对于单船具有容错性和适应性等优点，在舰队协同作战、大洋航行补给、石油天然气探测、环境监测、自动牵引作业中得到广泛应用。无人水面艇（Unmanned surface vessel）是一种新型智能水面机器人，具有侦察、探测、扫雷、情报收集、反潜等功能，近年在民用和军事领域得到广泛应用。目前，典型代表有英国“Springer”号双体USV、美国的“SpartanScout”、以色列的“Protector”等。

船舶编队控制方法可分为行为控制法［1-2］、虚拟结构法［3］、势函数法［4］、领导跟随法［5］等。行为控制法给编队中逐一指定一些包括队形保持、障碍物避让、目标搜索等预期行为。通过各行为的加权形成整个编队的期望行为，不基于个体准确模型。领导跟随法是基于多智能体群集运动控制的概念［6］，在由领航者和跟随者两种个体组成的群体模型中，跟随者通过相互间的局部感知和相互协同作用，与领导者保持状态相似，使船队整体最终呈现一致行为。在船舶编队领域，领导跟随法属于协同目标跟踪。具体方法是指定一艘船为引导者，引导者跟踪事先定义好的路径轨线，其他船舶只需跟随引导船的特定参考位置，可以是船舶中心，也可是船外某一虚拟位置，灵活多变、简单易行，参看图1。虚拟结构法中，将整个编队作为一个刚体结构，编队成员跟踪其在刚体上对应的固定点，并使用队形反馈防止单艘船掉队，在一定程度上可看作领导跟随法的一个变体。编队控制中大多采用此两种方法相互结合，发挥彼此优点。

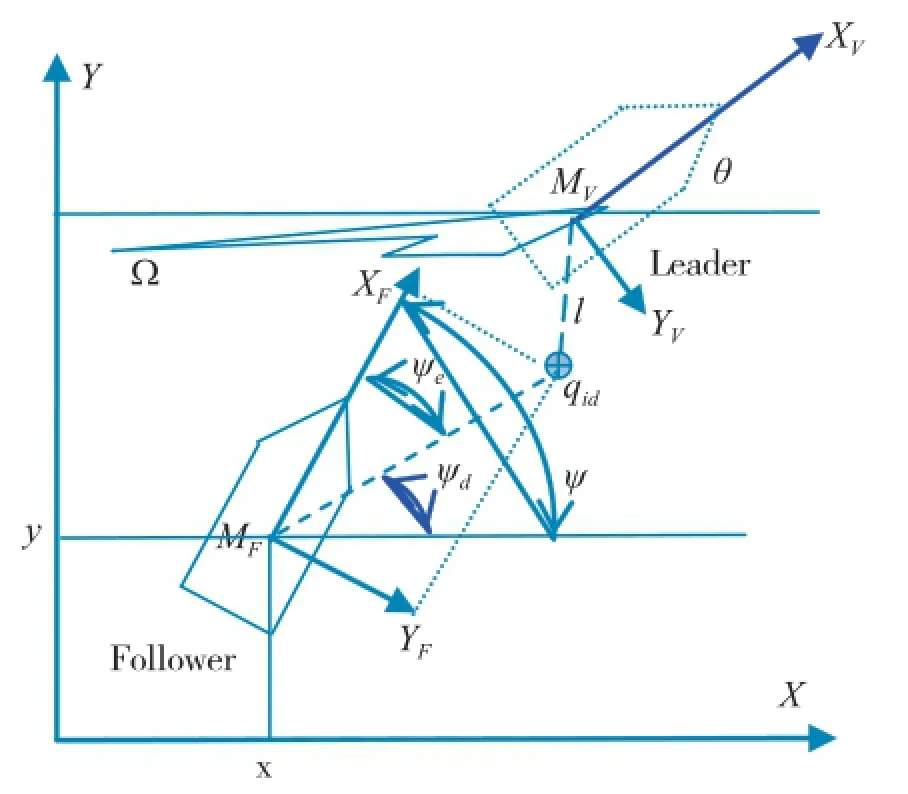
图1 领航船舶和跟踪船舶队形结构

船舶编队协同控制，可利用协同路径跟踪和目标跟踪来实现。协同路径跟踪［7］，提前设定好每艘船的期望路径，利用通信网络，实时交互各艘船行驶速度及路径参数，直接在模型控制中加入队形协调反馈，使这些参数达到一致。但是需引入辅助状态变量，并且每艘船的路径需要提前设定好，实现较为繁琐。采用目标跟踪［8］，可通过时空解耦思想使控制简单化。首先实现空间上单艘船的路径跟踪控制，采用基于引导跟随法追踪划定路径上的虚拟船舶，使之能够按指定路径航行，参看图1。队形控制，即船舶在跟踪路径同时使速度趋于一致，属时间域协同。通过时间域内的速度协同与空间域上的路径跟踪实现队形控制，但两者无优先顺序。例如，如果队形中引导船速度过快，跟随船位置偏差过大，那么降低引导船速度，控制器会使跟随船加速跟上引导船，缩小位置差距，保持既定队形。当偏差距离缩小后，可以增大引导船速度，跟随船在控制器作用下相应提高速度跟随虚拟参考点，保持船舶队形。

编队首先需要解决单艘船舶的路径跟踪问题。国内外的许多学者对此作了大量的研究，取得了丰硕的成果，参见综述［9］。大部分船舶在横向没有配备驱动装置（例如侧推装置），船舶只能通过纵向主机推力和舵机控制前进速度和方向，不能直接控制横向运动，都属于欠驱动［10］。实际船舶由于其复杂性、水动力阻尼、未建模动态、环境干扰等，难以量化精确，得不到精确的模型。文献［11］取消了船舶附加质量，阻尼矩阵为对称阵假设，加入非线性阻尼和风浪干扰，设计了全局鲁棒控制器。由于采用 Lipschitz映射算法自适应估计非线性项，使控制器比较复杂，其仍然是基于模型的控制［12］。该文献也研究单个水下航行器的目标跟踪问题，基于反步法和领导跟随策略设计了自适应位置跟踪控制器。文献［13］利用模糊控制器，研究具有鲁棒效应的自适应船舶控制器来跟踪直线航迹。文献［14］利用单神经网络对模型未知不确定项进行估计（未考虑时变干扰项），基于协同路径跟踪，实现了编队的自适应鲁棒控制。文献［15］利用RBF神经网络作为前馈补偿，设计了全局稳定自适应的鲁棒路径跟踪控制器（属于单艘船舶路径跟踪），但是高斯函数中心点及带宽的选择在实际应用中需试凑。文献［16］在周期时延通信拓扑条件下，首先利用控制器控制单船跟踪期望路径实现空间位置跟踪，然后同步路径参数，间接协同多无人艇的速度，实现整体编队。文献［17］利用RBF神经网络估计模型全局未知项和时变干扰项，设计了全驱动船舶路径跟踪控制器（单艘船舶控制，非编队）。

本文采用基于领导-跟随的目标追踪方法。利用自适应单隐层神经网络处理船舶模型中非线性动态和环境的时变干扰。在运动学控制中，选取跟随船舶与参考点的偏差作为跟踪误差，设计运动学虚拟跟踪控制器。利用运动学跟踪误差，扩展建立动力学误差方程，并采用反步递推技术求解出所需控制变量。可以在线学习补偿非线性动态及阻尼，未建模水动力和环境干扰，控制器全局稳定且不依赖于船舶精确模型。采用一阶滤波器［18］代替微分项避免了控制器反步设计的微分膨胀问题。通过解耦协调控制，只需设计单艘船舶基于领导跟随的控制器，便可以完成编队控制。减少了控制器设计的复杂性。

1　船舶运动模型与问题描述

1.1 运动学和动力学模型

在建立船舶运动和动力学模型时，采用随船坐标系和大地坐标系。随船坐标系以船舶重心为原点，船首和右舷方向为水平坐标轴。大地坐标系以正北正东方向为水平坐标轴，垂直指向地心为垂直坐标轴。本文考虑未知非线性项，给出模型详细描述［10］。式中：为大地坐标系下船舶位置和首摇角。为随船坐标系下纵向速度、横漂速度和首摇角速度。τiu为纵向推力；控制输入向量；τir首摇力矩。为风、浪、洋流干扰。为未建模动态。、

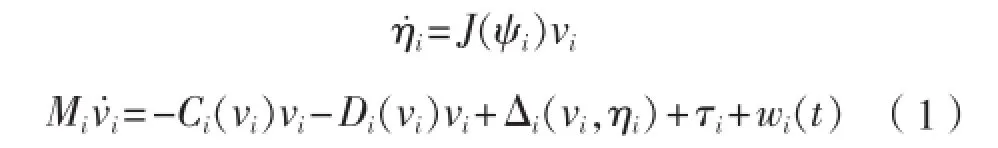
为惯性矩阵、向心力矩阵和水动力阻尼阵。

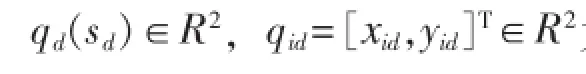
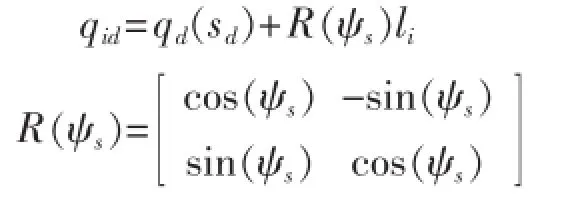
为追踪目标点 ，定义追踪误差

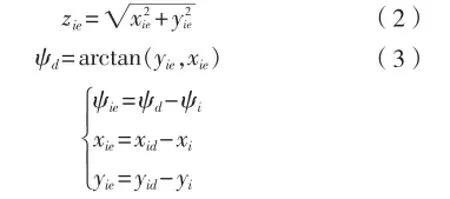
（注释：ψd是跟随船舶相对于目标点的角度，即跟随船头一直朝着目标点，控制思想是以最直接快速的方法到达目标点，没有综合考虑船舶的其他状态，例如在达到追踪点时是否速度过快，首摇角偏差是否太大，未考虑跟随船舶的未来状态与期望的领导船舶状态一致。ψd采用引导船舶首摇角， 有预测控制效果，使跟随船追踪与引导船相同的航向。在达到追踪点后，船舶航向与引导船航向相差无几。）

1.2 神经网络

采用前馈神经网络估计不确定动态。

单隐层（SHL）网络，输入xk，输出 yi，映射函数为

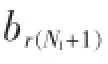
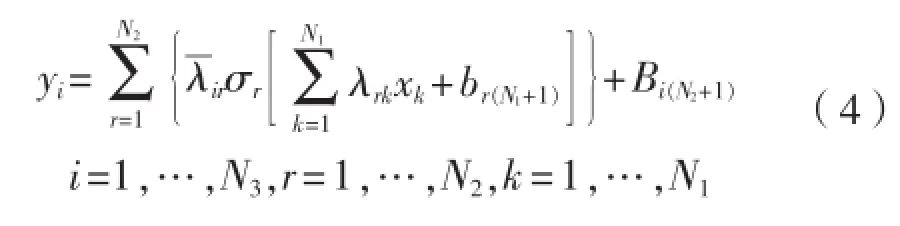
2　控制器设计

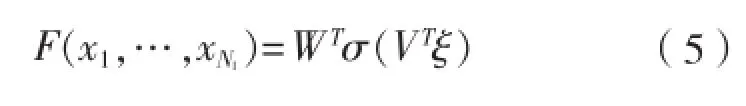
根据全局估计定理［17］，给定一个连续实函数，总存在一个理想权重矩阵V、W、使得误差， 是W、V的估计值。隐层节点 输出误差：函数估计误差：

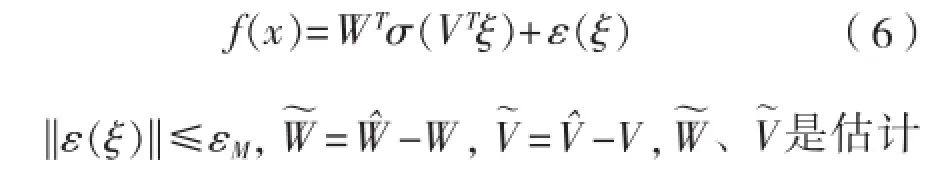
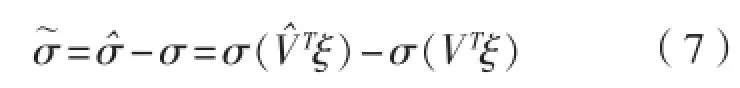
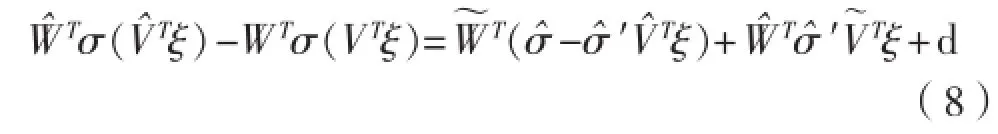
1.3 假设条件及控制目标

（1）干扰有界

2.1 首摇控制

直接利用反步法求解首摇偏差动态，对

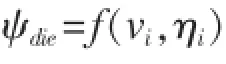
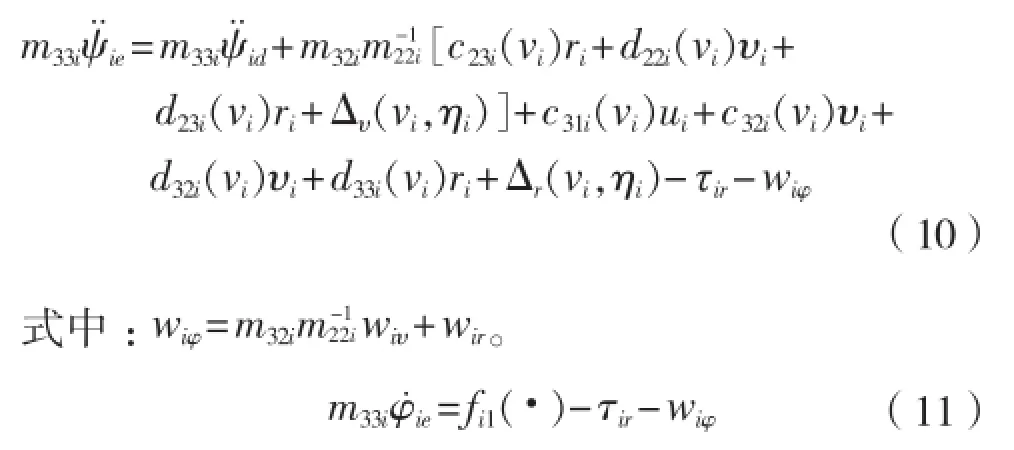
（注：直接反步法求τir，求导运算量很大，此处直接可得出τir的表达式。）

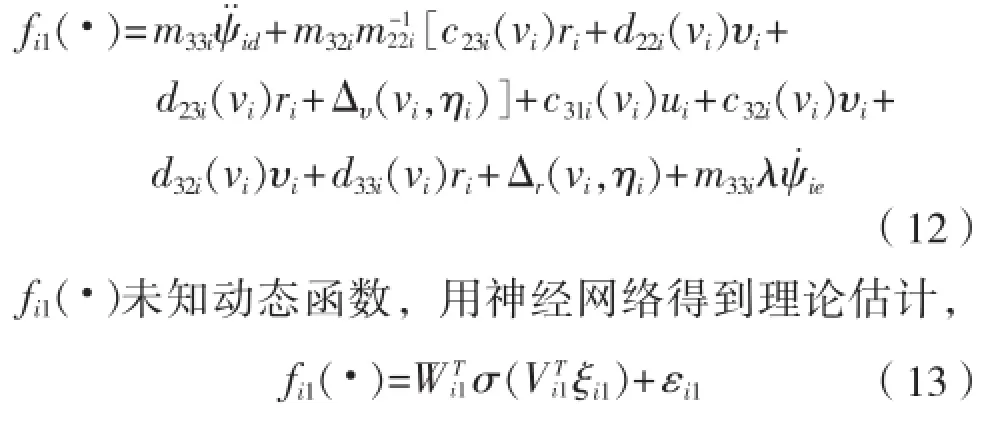
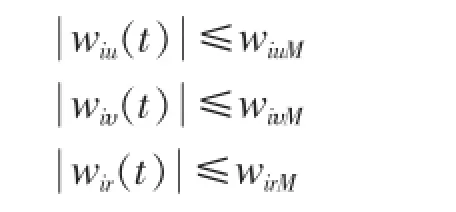
（2）横漂速度υi无源有界

在横向运动中，实际水动力阻尼力起主要作用，横向速度受阻尼作用，是有界的。

（3）速度状态可观测

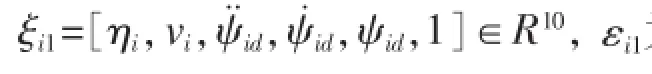
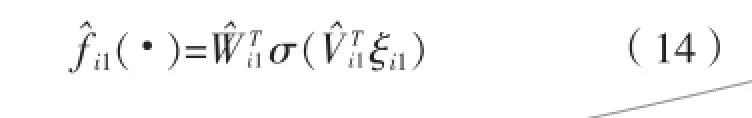
自适应率取：

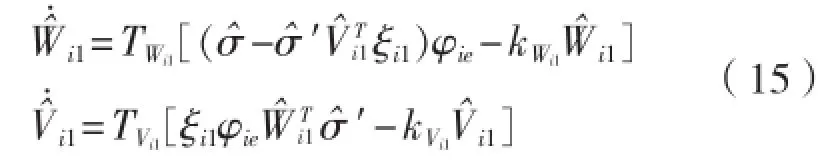
因此控制器为：

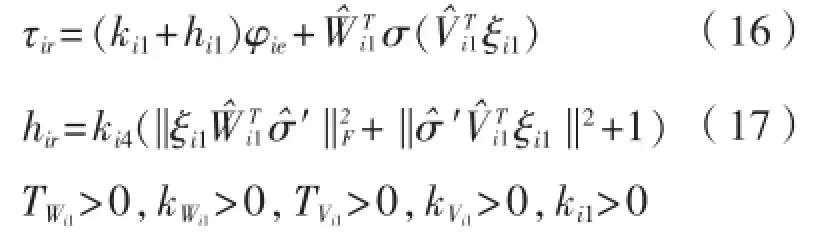
将控制项式（16）带入式（11）得：未知动态项估计误差为：

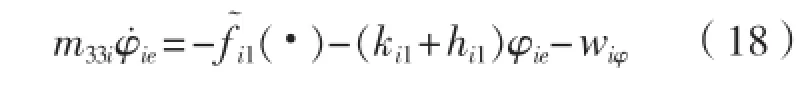
整理式（18）得：

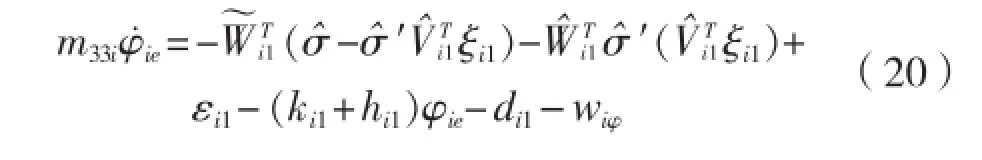
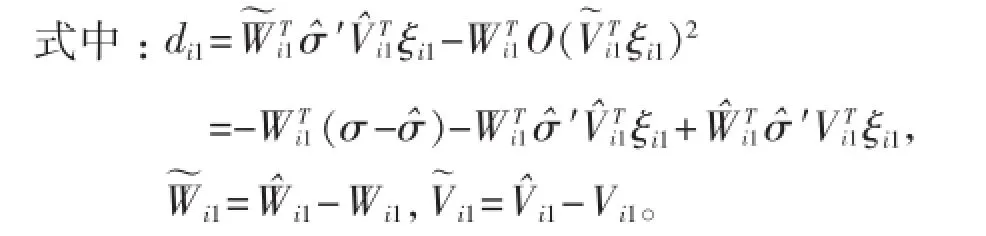
2.2 纵向控制

纵向控制直接采用反步法求出控制变量表达式。

直接求导zis，联立（2）、（3），简单计算整理得取uid为ui的虚拟控制量，定义误差为：令

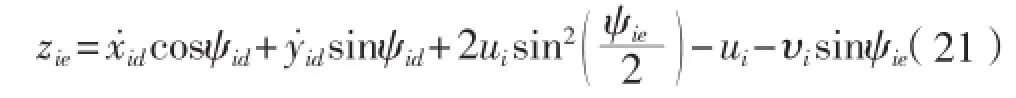
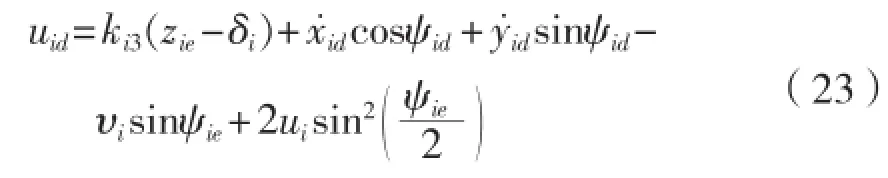
［12］，取。定义第一个Lyapunov函数。

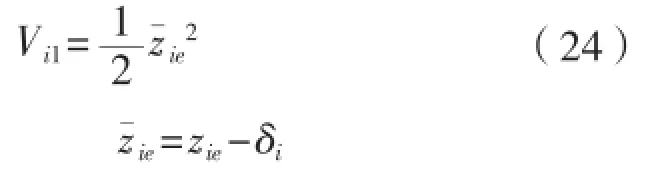
对式（24）求导，结合式（21）、式（22）和式（23）得到：对（22）求导，结合式（1）得到：

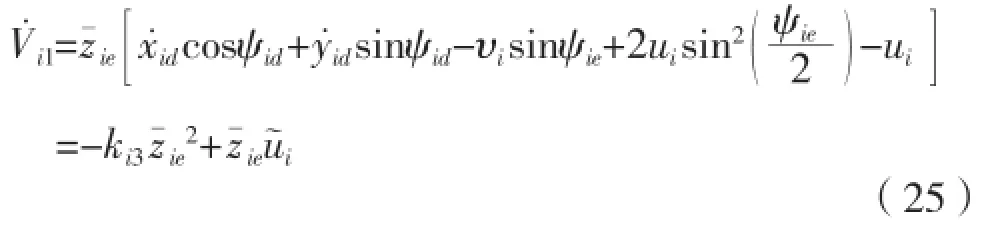
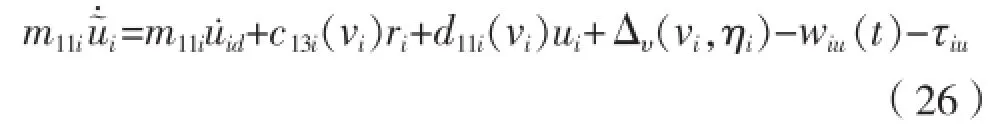
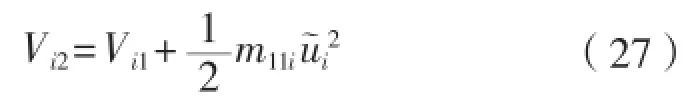
定义第2个李氏函数：对式（27）求导，结合式（26）得：

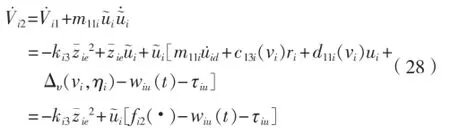
其中：

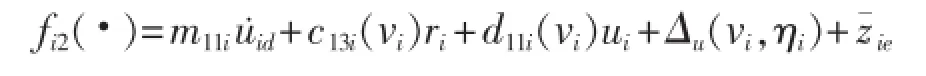
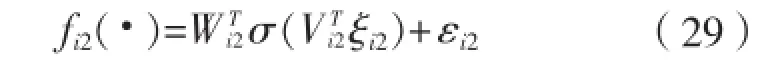
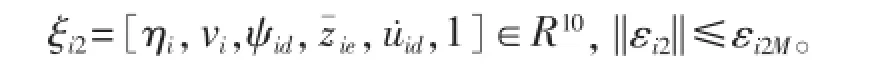
用神经网络估计：类似于式（14）取自适应项：自适应率为：设计纵向控制器τiu：

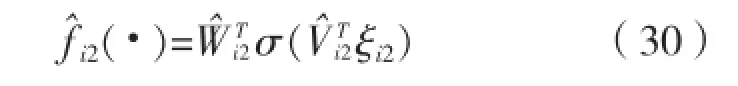
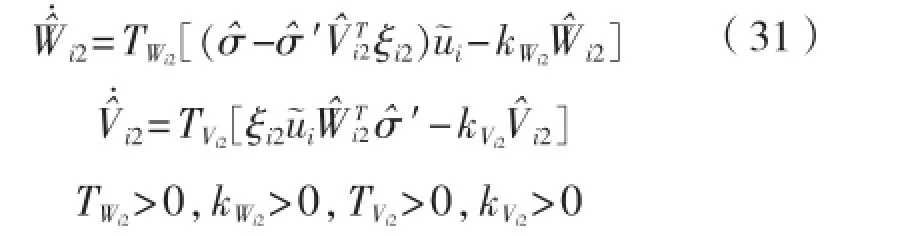
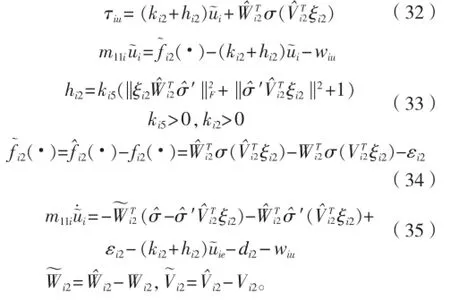
3　稳定性分析

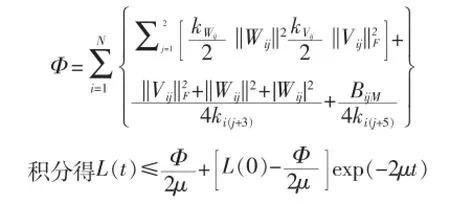
考虑由N艘船舶组成的编队，分析在控制器（16）、（17）、（32）、（33），自适应控制器（14）、（30）作用下闭环系统的稳定性。

证明：构造李氏函数

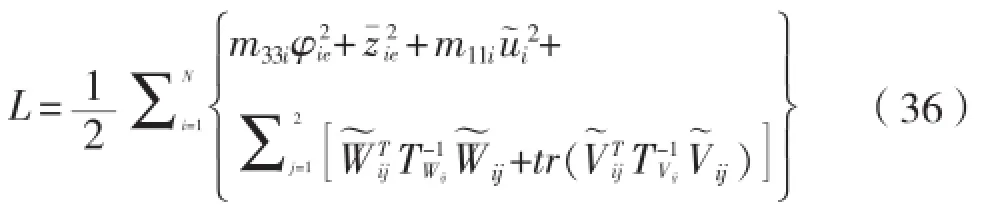
两边求导

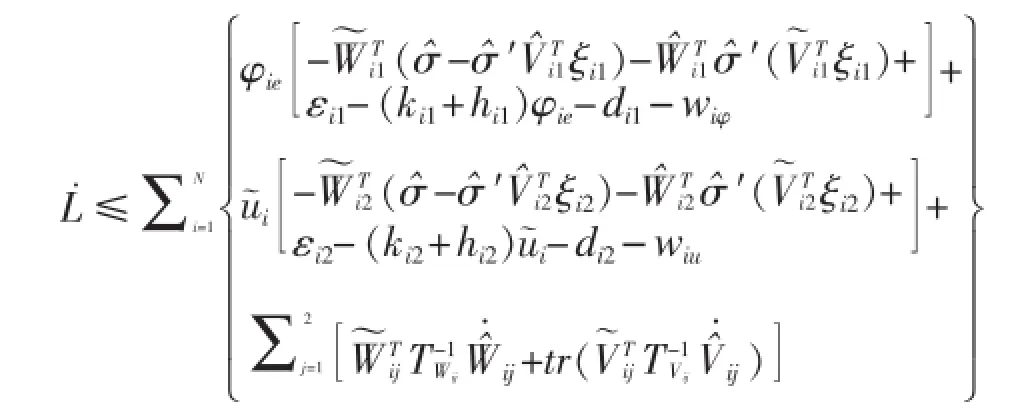
3.1 仿真验证及分析

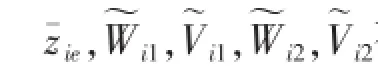
将神经网络权重自适应率

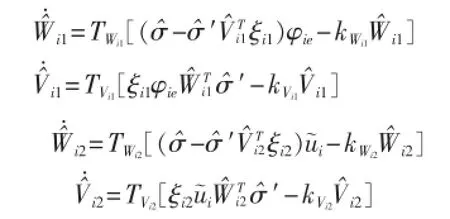
带入，利用Young的 不等式，经整理最终得到

参见图1，设定期望追踪点qid与领导船位置相距2 m，即l=2。线段MVqid与MVYV夹角为30°。两艘船舶跟踪位置左右对称，船舶队形为等腰三角形。

神经网络估计动态误差如下页图3所示，表明神经网络在所设计的调整率下，能够很好地估计未知非线性项。

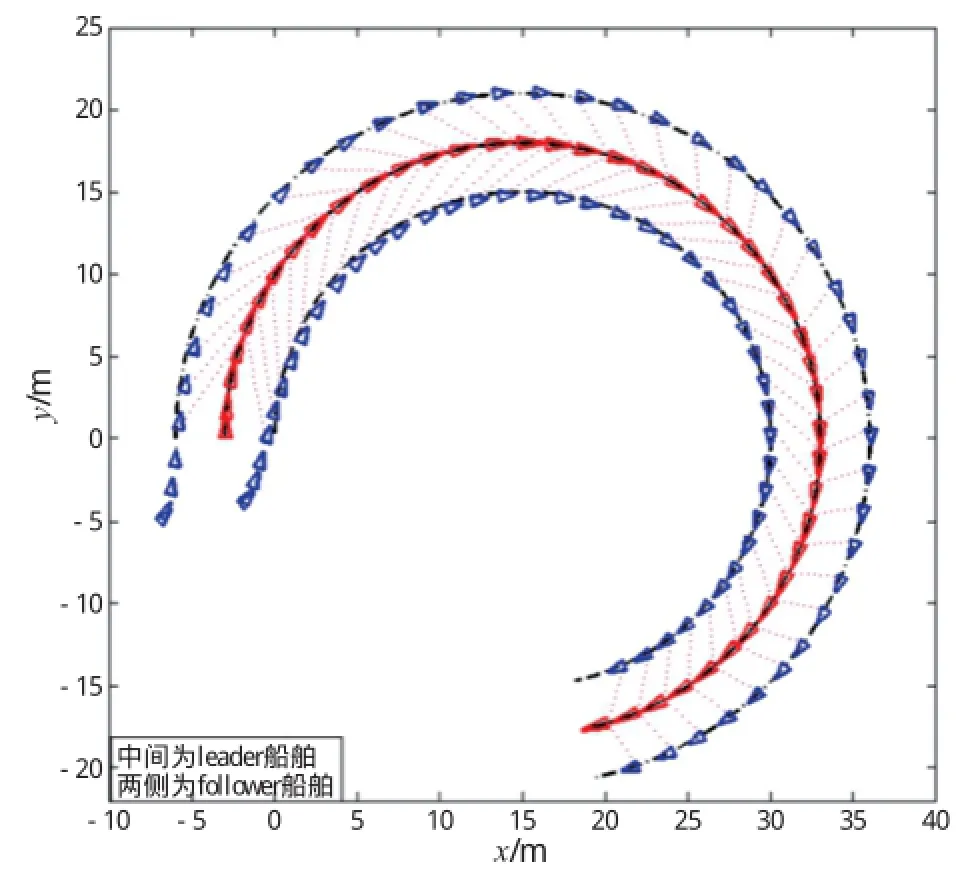
图2 路径队形图

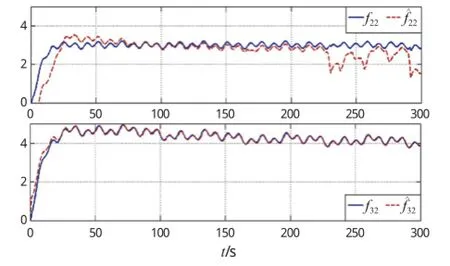
图3 神经逼近误差

图4表明，在提出的控制器下，速度跟踪误差，航向角误差，距离误差收敛到原点的一个小的邻域内，经仿真验证，适当增大控制增益，误差邻域会进一步缩小。

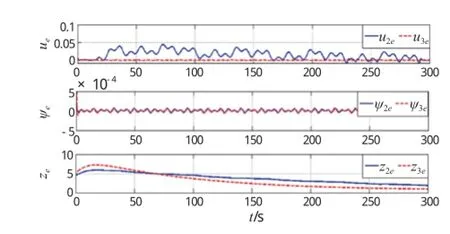
图4 跟踪误差

图5表明控制力没有发生跳跃，并处于有界范围内，与实际相符合。

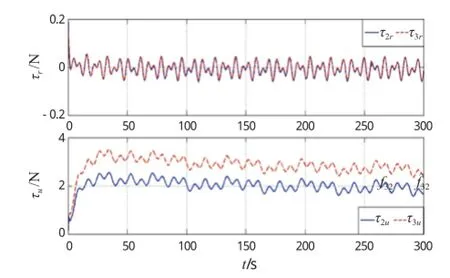
图5 控制效果

4　结　论

本文综合利用反步法、自适应神经网络和动态面技术，对多艘无人艇的协同编队控制进行研究。与基于精确模型方法相比，利用神经网络估计补偿模型中存在的非线性动态以及环境干扰等不确定性因素。针对协同编队控制控制器结构复杂性问题，采用动态面技术代替微分项，降低了对控制器结构设计的复杂度。利用时-空解耦方法，将路径跟踪和引导跟随目标跟踪方法相结合，通过控制虚拟船参考速度间接实现了船舶编队控制。闭环系统的李雅普诺夫分析证明系统是有界稳定的。仿真结果表明，结合神经网络自适应控制方法的控制器是简洁有效的。

［参考文献］

［ 1 ］ IHLEI A F， ARCAKM， FOSSENT I. Passivity-based designs for synchronized path following， Proceedings of the 45th IEEE Conference on Decision and Control，2006，4319-4326.

［ 2 ］ BALCH T.ARKLNRC.Behavior-based formation control for multi-robot teams［J］.IEEE Transactions on Robotics and Automation，1998（6）：926-939.

［ 3 ］ 袁健，唐功友.采用一致性算法与虚拟结构的多自主水下航行器编队控制［J］.智能系统学报，2011（3）：248-253.

［ 4 ］ Do K D.Formation control of underactuated ships with elliptical shape approximation and limited communication ranges ［J］.Automatica，2012（7）：1380-1387.

［ 5 ］ FAHIMI F. Sliding-mode formation control for underactuated surface vessels［J］.IEEE Transactions on Robotics，2007（3）：617-622.

［ 6 ］ 刘佳，陈增强，刘忠信.多智能体系统及其协同控制研究进展［J］.智能系统学报，2010（1）：1-6.

［ 7 ］ JOAO ALMEIDA，CARLOS SILVESTRE ，ANTONIO PASCOAL. Cooperative path-following of mutiple surface vessels with parameters model parametric model uncertainty and in the presence of ocean currents ［J］. International Journal of Robust and Nonlinear Control，2013（14）： 1549-1565.

［ 8 ］ BREIVIKM，HOVSTEINV.E， FOSSENT.I，Ship formation control：a guided leader-follower approach，Proceedings of the 17th IFAC World Congress，Seoul，Korea，2008.

［ 9 ］ 郭晨.欠驱动水面船舶运动控制研究综述［J］.控制与决策，2009（3）：321-329.

［10］ Do K D，PAN J.Robust and adaptive path followingfor underactuated ships［J］. Automatica， 2004（3）：929-934.

［11］ Do K D，PAN J.Global robust adaptive path following of underactuated ships［J］.Automatica，2006（2）：1713-1722.

［12］ CUI. Leader-follower formation control of underactuated autonomous underwatervehicles［J］.Ocean Engineering，37（17/18）：1491-1502.

［13］ 李铁山，杨盐生，洪碧光，等.船舶航迹控制鲁棒自适应模糊设计［J］.控制理论与应用，2007（3）：445-448.

［14］ WANG D，PENG Z.Robust adaptive formation control of underactuated autonomous surface vehicles with uncertain dynamics［J］.IET Control Theory and Applications，2013（12）：1378-1387.

［15］ CHEN W S， JIAOL.C.Globally stable adaptive robust tracking control using RBF neural networks as feedforward compensators， Neural Computation and Application，2010（2）：351-363.

［16］ ALMEIDA J， SILVESTREC， PASCOALA. M. Cooperative control of multiple surface vessels with discrete-time periodic communications， International Journal of Robust and NonlinearControl， 2012（3）： 398-419.

［17］ TEE，Petal K. Control of fully actuated ocean surface vessels using a class of feedforward approximators［J］. IEEE Transaction on Control System Technology，2007（4）：750-756.

［18］ WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of unertain nonlinear systems in strictfeedback form［J］.IEEE Transactions on Neural Networks，2005（1）：195-202.

Ship track control based on leader-follower

QI Xiao-wei REN Guang
(Marine Engineering College, Dalian Maritime University, Dalian 116026, China)

Cooperation formation control is very important for the unmanned surface vessels （USVs） in military and civil applications. The cooperation formation control for multiple USVs with model uncertainty and the unknown wave-current interference is achieved through the multi-agent aggregation model based on the target tracking by the leader-follower. Moreover， the unknown items and the environmental interference for the whole ship is approached through single hidden layer neural network， and the fi rst-order fi lter is introduced to replace the diff erential items in the backstepping calculation， signifi cantly decreasing the amount of calculation. By the timespace decoupling method， the decentralized cooperation formation control will be indirectly reached through the interactive track information for each ship. It is proved that the situation and signals of the closed-loop system are converged to a bounded set by using Lyapunov stability analysis method. The error of the control accuracy becomes arbitrarily small by selecting proper parameters. The control algorithm is then validated by the simulation results. Keywords: unmanned surface vessel； neural network； uncertainty； multi-agent system； fi rst-order fi lter； formation control

TP273

A

1001-9855（2016）01-0092-08

2015-09-07

齐小伟（1983-），男，硕士，研究方向：轮机工程。任 光（1952-），男，博士，教授，博士生导师，研究方向：轮机自动化与控制，复杂系统建模。