复杂网络理论在船舶电力系统结构脆弱性分析中的应用

张洪涛吴世君

（1. 中国人民解放军海军92132部队25分队 青岛266000；2. 中国人民解放军海军92337部队 大连116025）

复杂网络理论在船舶电力系统结构脆弱性分析中的应用

张洪涛1吴世君2

（1. 中国人民解放军海军92132部队25分队 青岛266000；2. 中国人民解放军海军92337部队 大连116025）

文章将复杂网络理论分析方法应用于船舶电力系统结构脆弱性的分析。首先将船舶电网抽象为复杂网络模型，并对该网络模型的结构特征进行计算和分析；然后通过分析节点攻击后的电力系统性能对船舶电网结构脆弱性进行分析。结果表明：船舶电网的脆弱性与网络拓扑结构密切相关，利用复杂网络理论可以有效确定电力网络的关键节点。

船舶电力系统；结构脆弱性；复杂网络理论；介数；度

引言

区别于陆地电力系统，船舶电力系统（SPS）是典型的独立电力系统，发电机组的容量和冗余较小，对故障和破坏更加敏感，因此船舶电力系统的主要任务是从生命力角度保证提供稳定、连续和可靠的供电。船舶电力系统供电连续性与其电网结构脆弱性有密切联系，因此有必要设计一种适用于分析船舶电网结构脆弱性的方法，以评估系统供电连续性，并寻找对供电连续性具有关键影响的节点和支路，从而优化电网设计。

随机网络［1］和小世界网络［2］的概念分别在1959年和1998年提出，而标度网络的特性在1999年［3］开始被分析，这些网络模型构成了复杂网络理论研究的基础。复杂网络理论在陆地电力系统中的应用包括两个方面：大范围停电的机理［4-5］和电网结构脆弱性的分析［6-11］。

与陆地电网类似，船舶电力系统也可以描述为若干节点通过支路以某种方式相连构成的拓扑网络。电网拓扑结构随着工作状态的变化发生显著变化，是具有代表性的复杂网络。在复杂网络理论中，有多种统计指标和评价方法用于描述网络节点重要性和分析网络性能。因此，可以借鉴和引入复杂网络理论用于分析船舶电力系统的结构。

本文通过将电网元件描述为支路，相邻元件之间的连接点描述为节点，建立了船舶电网的拓扑模型。在拓扑模型的基础上，分析了船舶电网的拓扑特性。为评估重要节点和舱室节点组，定义了两个评价指标。通过对典型的船舶电力系统进行随机攻击和蓄意攻击测试，验证了所提出的评价指标的有效性。最后，定义了舱室电气介数指标用于分析船舶电网的结构脆弱性。

1　船舶电力系统

船舶电力系统与陆地电力系统相比，具有以下不同之处：

（1）发电机容量与负荷容量相当，容量裕度不足，主配电板故障将导致功率缺失和负荷失电。

（2）船舶电网供电面积相当陆地电网要小。对船舶的打击将造成多个元件故障。

（3）一些重要的负载对失电十分敏感，因此重要负载有多路供电路径。

图1为典型的船舶电力系统拓扑模型。该系统包含4台发电机组，通过主配电板和跨接线连成了一个环形。重要负载通过正常和备用供电路径获得供电，其中正常供电路径是优先供电路径。负载在任何时候仅有一路供电。断路器（CB）可以隔离故障并完成失电负载恢复供电操作。

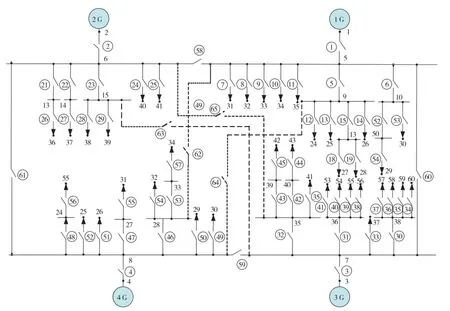
图1 船舶电网拓扑模型

2　船舶电网拓扑特性分析

在复杂网络理论中，有4类基本的统计指标用来分析网络的结构特性，包括：度、平均路径长度、聚类系数和介数。本节将通过计算这4个统计指标来分析图1所示的船舶电网结构特性。

2.1 度指标

节点i的度是指与节点i相连的边的数量。对于有向图，节点的度分为出度（out-degree）和入度（in-degree）两类，其中，出度是指由该节点指向其他节点的边的数量；入度是指从其他节点指向该节点的边的数量。度指标描述节点i与相邻节点的连接关系，反映其在网络中的重要程度。如图1中的10号节点与6号、52号、53号等3条支路相连，其度指标取值为3。

对图1所示的电网中各节点的度指标进行计算，平均度指标为2.07。图2（a）采用双对数坐标系给出了节点度累积分布曲线图，其中用符号“o”表示度指标计算结果，用“*”表示指数函数y=k-1.5分布曲线。图2（b）为用直方图表示度的分布。

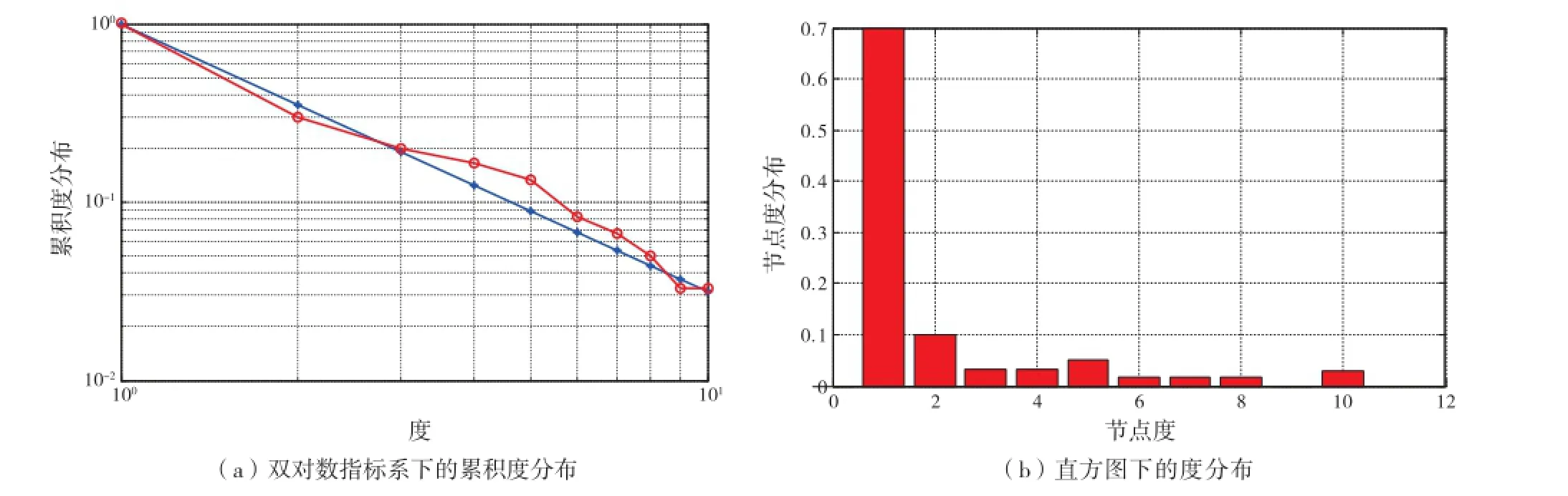
图2 累积度分布曲线和度分布直方图

通过图2（a）可以看出，累积度分布指标在双对数坐标系下具有线性特征，且与指数函数特性接近。这表明在电网中有部分节点度指标高，这点在图2（b）中也可以看出。分析结果表明船舶电网是一种具有标度网络特性的复杂网络。

2.2 平均路径长度指标

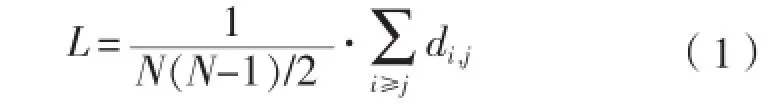
节点i和j之间的距离di，j定义为该两节点之间最短路径所含的总边数。网络的平均路径长度L定义为网络中所有节点对之间的最短距离的平均值，如式（1）所示。式中：N为网络节点总数。另外，平均路径长度又称为特性路径长度。例如图1中的5号节点到30号节点的最短路径包含的支路为6号、53号支路，则5号与30号节点之间的距离d5，30=2。

图1所示的电网的平均路径长度指标L为3.57，小于陆地电力系统。

2.3 聚类系数指标

假设网络中的某一节点i有ki条边将它与其他节点相连，这ki个节点之间存在的边数Ei和所有可能的边数ki（ki-1）/2之比即为节点i的聚类系数Ci，即聚类系数Ci的另一种表述为：

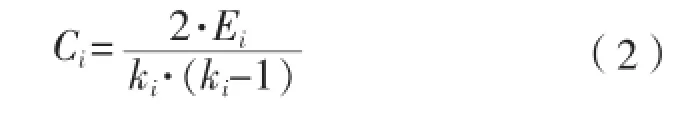
若图1中的10号节点分别与30号、50号节点相连，但30号与50号节点之间无连接的支路，则10号节点的聚类系数为0。

图1所示电网的所有节点的聚类系数均为0，说明在船舶电网中没有三角形连接的节点组， 这表明船舶电网没有小世界网络的特性。

2.4 介数指标

介数可分为节点的介数和边的介数两类。其中，节点i的介数bi是指网络中通过该节点的最短路径的数量占所有最短路径的比例，即

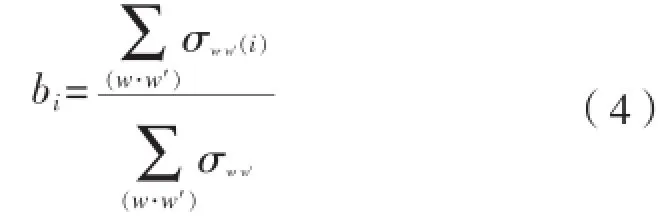
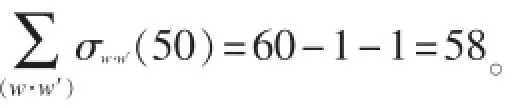
对图1所示的电网中各节点的介数指标进行了计算，图3采用双对数坐标系给出了的累积介数分布。其中用符号“o”表示介数指标计算结果，用“*”表示指数函数y = k-1.5分布曲线。

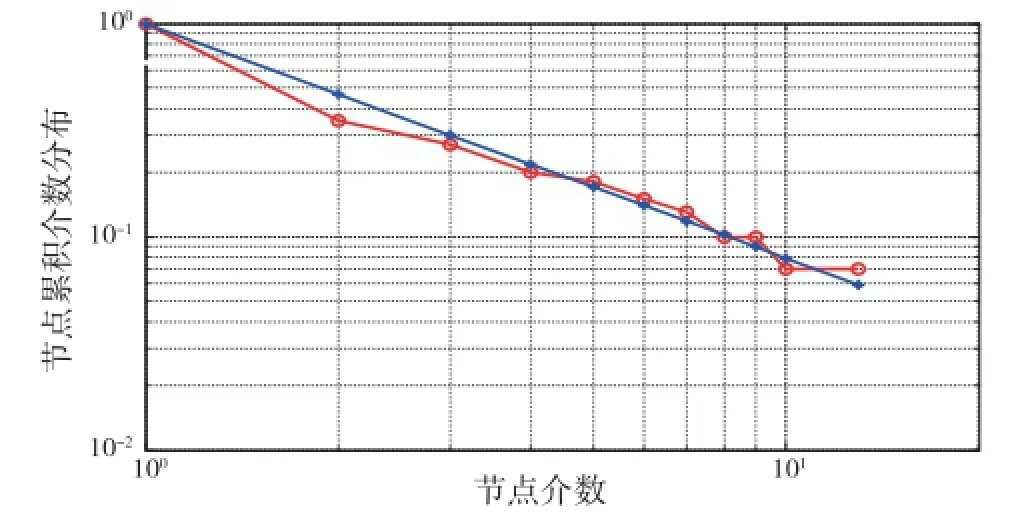
图3 累积介数分布曲线

从图3中可以看出，累积介数分布指标在双对数坐标系下具有线性特征，且与指数函数特性接近。这说明船舶电网中的大部分节点的介数指标较低，而有少部分节点介数指标较高。

以上4个指标计算结果表明船舶电网属于一种标度网络，而并非小世界网络或随机网络。船舶电网显示出区别与陆地电网的独特特性。

3　船舶电网结构脆弱性评估

研究电力网络分为两个方面：静态脆弱性和动态脆弱性。在动态脆弱性研究方面，当一些节点和支路负载移去，且系统面临隐藏的故障时，负载被认为需要重新分配，这将导致剩下的节点和支路会去掉。电网静态脆弱性主要是在一些支路和节点去掉后，分析电网的性能。

3.1 船舶电力系统性能评估指标

船舶电力系统在攻击损伤后的评估指标可以分为以下4类：

（1）全局评估指标基于最短路径。这一指标包括平均地理距离，平均反向地理距离等，主要是计算两节点之间的最短距离。系统脆弱性一般随最短距离的增加而变差。

船舶电网节点间距离短，电网功率流动不会受制于节点的最短距离。电网负载的功率取决于发电机组的功率。该指标不能反映损伤的严重性，因此最短距离不适合分析船舶电网性能。

（2）局部评估指标基于联通性分析。聚类系数是典型的分析局部电网性能的评价指标，可用来分析故障状态下的联通性。

（3）连接子网的最大范围。若系统因故障而解列，可以用最大连接子网的节点数与节点总数的比值来描述受损情况，按式（5）计算：

式中：N0是故障后节点总数；Ni是故障后第i个子网的节点数；n为故障后的子网个数。

在船舶电网中包含一些发电机组，当系统因故障解列后，一些子网会失电，而含有发电机的子网将为子网内的负载供电。无论失电子网的规模多大，在失电后不必再考虑。因此，子网最大规模指标不适于评价损伤情况。系统剩下的总负载应作为分析船舶电力系统的静态脆弱性。

（4）故障后系统剩余的功率总量。当电力系统元件损坏后，系统将分解为M个子网，其中含有发电机组的子网有N个。剩余的功率总量可按式（6）计算：式中：gi为子网i的发电机功率总量；pi为子网i的负载功率总量。因此，min｛gi， pi｝为子网i所能承担的剩余负载功率总量。

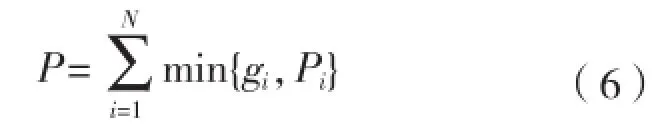
剩余负载功率总量指标反映了船舶电力系统在故障后持续向负载供电的能力，但未考虑各类船舶电气负载的重要性等级。

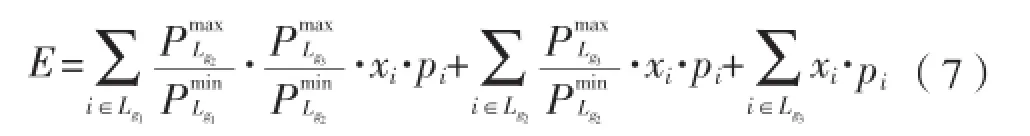
本文从满足船舶电气设备供电这一基本要求出发，充分考虑舰船电力系统中各负载的重要性等级，提出电网性能指标E用于评价故障后船舶电力系统供电能力，其表达式为：式中，Lg1、Lg2、Lg3依次为1级至3级负载的编号集合；pi为负载i的额定功率；xi为负载i所对应的状态变量，它用于表征故障后负载i的运行状态，若因电网受损而最终导致负载i停运，则有xi= 0，反之则xi= 1；、分别为2级、3级负载中单个负载额定功率的最大值，、分别为1级、2级负载中单个负载额定功率的最小值。该指标值越高，说明故障后舰船电网的性能越优。

通过对船舶电网的元件进行打击，并计算打击后的电网性能指标，可分析船舶电力系统的静态脆弱性。

3.2 节点蓄意攻击下的结构脆弱性分析

本文分别采用如下4种方式对舰船电网中的元件进行攻击：

（1）随机对电网中的20个节点进行攻击（RAN）；

（2）依次对电网中度最高的前20个节点进行攻击（ID）；

（3）依次对电网中介数最高的前20个节点进行攻击（IB）。

图4给出3种不同的攻击模式下，电网性能的下降趋势。表1给出各轮攻击下的电网性能指标。

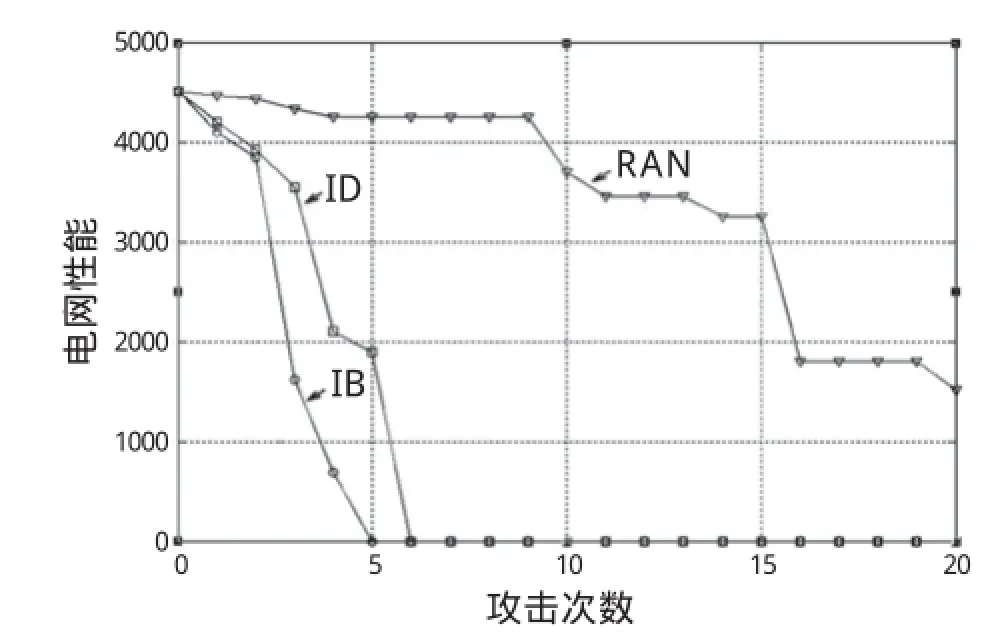
图4 3种元件攻击模式下的电网性能下降趋势

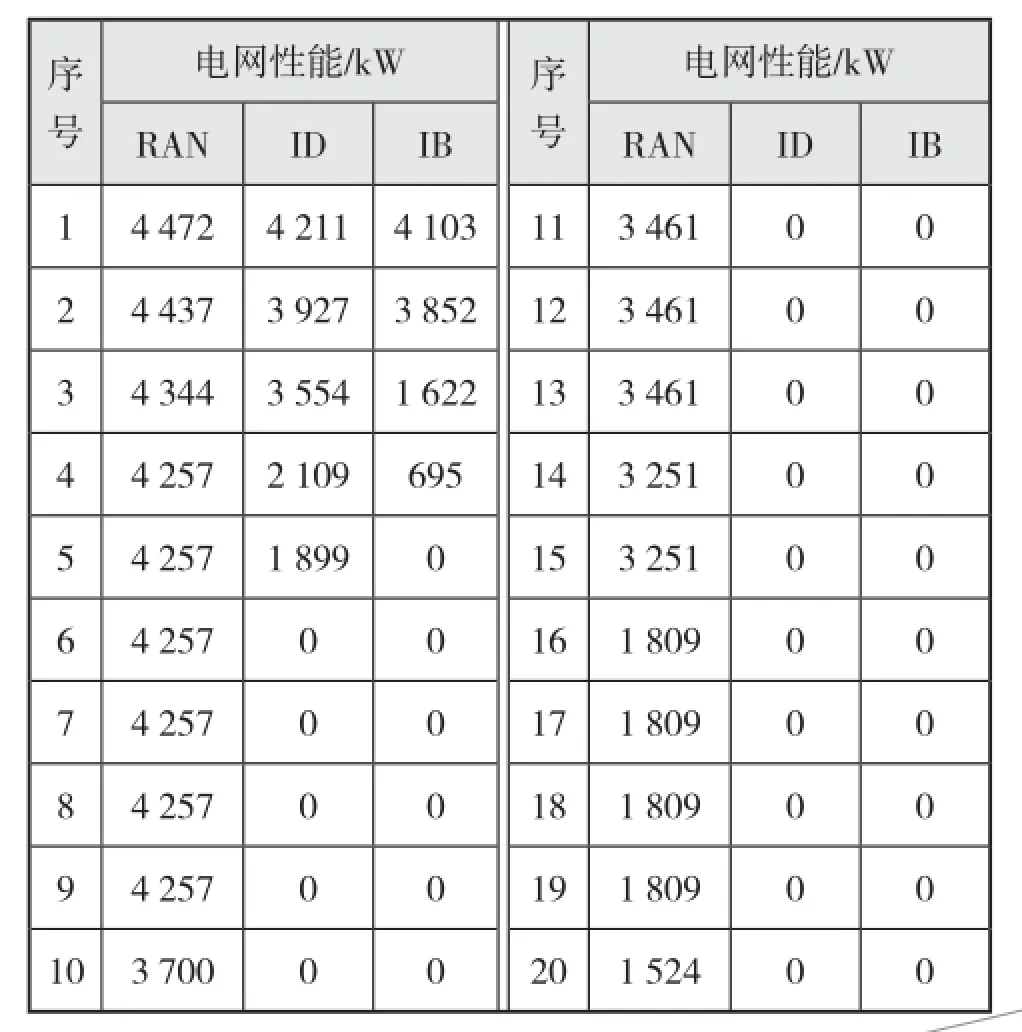
表1 4种元件攻击模式下电网性能指标

由图4和表1可见，舰船电网在随机攻击（RAN）下表现出较强的鲁棒性，经过20轮攻击后，电网性能的评价指标值由受攻击前的4 500 kW下降为1 524 kW，仍有部分负载能继续运行。而在按节点的介数对电网依次攻击时，电网性能的下降趋势最快，在经过5次攻击后，电网中的所有负载就全部停运，电网性能下降到零。分析结果表明，介数指标高的节点受攻击后，网络性能下降快，表明对应节点为船舶电网的关键节点，应予以重点防护以保障电力系统生命力。如图1中的5、6、7、8号节点分别对应于前后主配电板母线，其损坏将对电力系统供电能力造成巨大影响，应予以重点防护；同时，应增加重要负载的供电路径（相当于增大式（4）中节点之间最短路径总量σww′，减小重点节点介数），保证重要负荷在正常供电路径失电时，可以从备用供电路径供电，提高船舶电力系统的生命力。

4　结　论

船舶电力系统生命力是船舶电力系统设计时需要考虑的主要因素之一。从网络理论方面考虑，分析船舶电力系统生命力可根据船舶电力系统的结构和运行特性，通过建立其复杂网络模型，分析其脆弱性来实现。

本文将复杂网络理论应用于船舶电力系统结构脆弱性分析。对船舶电力系统的结构特性进行了分析，对4种统计指标的计算结果表明船舶电网具有与陆地电网不同的结构特性。在不同攻击模式下，分析4电站船舶电网的静态脆弱性。结果表明：节点介数指标相对其他指标能够更好地评估电气元件和舱室的重要性，因此，设计时尽量降低电气介数指标可以提高船舶电力系统生命力。

［ 1 ］ Erdos P，Renyi A. On the evolution of random graphs Publ. Math. Inst. Hung［J］. Acad. Sci.， 1959（5）：17-60.

［ 2 ］ Watts D J，Strogatz S H. Collective dynamics of “small world” networks［J］. Nature，1998，393：440-442.

［ 3 ］ Barabasi A L，Albert R. Emergency of scaling in random networks［J］. Science，1999，286：509-512.

［ 4 ］ Albert R， Barabasi A L. Statistical mechanics of complex networks［J］. Reviews of Modern Physics， 2002，74：47-97.

［ 5 ］ Dobson I，Carreras B A， Lynch V E. An Initial Model for Complex Dynamics in Electric Power System Blackout［C］// Proceedings of the 34th Hawaii International Conference on System Sciences. 2001：710-718.

［ 6 ］ 张海翔， 吕飞鹏. 基于保护脆弱度加权拓扑模型下的电网脆弱性评估［J］. 中国电机工程学报， 2014（4）：613-619.

［ 7 ］ 吴旭， 张建华， 邱威， 等. 基于N-k故障的地区电网脆弱性评估［J］. 中国电机工程学报， 2012（4）： 93-99.

［ 8 ］ 魏震波， 刘俊勇， 朱国俊， 等. 电力系统脆弱性理论研究，电力自动化设备， 2009（7）： 38-42.

［ 9 ］ Carreras B A，Newman D E，Dobson I，et al. Evidence for self-organized criticality in a time series of electric power system blackout［J］. IEEE Transactions on Circuits and Systems，2004，51：91-97.

［10］ Motter A E，Lai Y. C. Cascade-based attacks on complex networks［J］. Physical Review E，2002，66：1-4.

［11］ Holme P，Kim B J，Yoon C N， et al. Attack vulnerability of complex networks［J］. Physical Review E.，2002，65：05619（1-4）.

Structural vulnerability analysis of shipboard power system based on complex network theory

ZHANG Hong-tao1WU Shi-jun2
(1. Navy of 92132, Qingdao 266000, China; 2. Navy of 92132, Dalian 116025, China)

In this paper， the complex network theory is applied to analyze the structural vulnerability of the shipboard power system. The shipboard power system is modeled as a complex network， whose topological characteristics are calculated and analyzed. Then， the structural vulnerability of the shipboard power system is analyzed through the performance of the power system after the node attack tests. The results show that the vulnerability of the shipboard power system greatly depends on the topological structure， and the complex network theory can eff ectively determine the key nodes of the power system.

shipboard power system； structural vulnerability； complex network theory； betweenness； degree

U674.7+03.3

A

1001-9855（2016）01-0081-06

2015-10-08；

2015-11-27

张洪涛（1971-），男，机电长，高级工程师，研究方向：舰船动力系统。吴世君（1980-），男，硕士，工程师，研究方向：舰船动力系统。