带月池深海钻井船摇荡运动性能分析

张晓宇胡开业周雯雯

（1.中国石油渤海装备研究院 海工装备分院 盘锦124010； 2.哈尔滨工程大学 船舶工程学院 哈尔滨150001）

带月池深海钻井船摇荡运动性能分析

张晓宇1胡开业2周雯雯2

（1.中国石油渤海装备研究院 海工装备分院 盘锦124010； 2.哈尔滨工程大学 船舶工程学院 哈尔滨150001）

海上钻井作业过程要求钻井船具备良好的稳定性能，而月池内流体柱的不规则振荡以及钻井船细长的船体外形都将对船体运动性能造成不利影响，从而限制其在恶劣海域的作业适应性。文章基于三维势流理论对带月池钻井船的摇荡运动进行预报，并通过船模试验对预报结果进行有效性验证。在此基础上，提出钻井船摇荡运动衡准值，对钻井船海上作业适应性进行研究，分析月池尺度和形状对钻井船运动性能的影响。

深水钻井船；运动预报；月池

引言

与其他钻井平台相比，钻井船的机动性好、自持力强、具有自航迁移能力，更能适应深水及超深水作业。截止2013年10月，全球现役钻井船总量为91艘，另外还有88艘正在建造中。在91艘钻井船中，83艘钻井船具备在4 000 ft（约合1 219 m）以上深水作业的能力，比例为91.2%，68艘钻井船适应于10 000 ft（约3 048 m）以上的超深水海域作业，比例达74.7%［1］。与国外蓬勃的发展现状相比，国内钻井船技术仅处于起步阶段。由于钻井船高附加值的特点，其相关技术垄断严重，研究成果为商业秘密，增加了国内钻井船技术的发展难度［2］。本文从运动性能的角度对钻井船技术进行研究，为国内自主船型的开发提供技术支撑。

海上钻井作业对平台运动性能要求苛刻，过大的运动幅度不仅影响钻井精度与作业效率，而且将缩短钻杆、隔水管等钻井设备的使用寿命，甚至导致皲裂、脱扣等安全事故，造成巨大的经济损失。然而，钻井船具有细长的船体外型，受波浪的常态影响，对运动性能造成不良影响。另外，钻井船中部布置有贯穿船底的月池结构，月池内流体振荡规律复杂、产生漩涡等非线性现象，影响流体域的压力分布及钻井船摇荡运动幅度，限制了钻井船在恶劣海域的作业适应性［3］。因此，钻井船在波浪中的摇荡运动预报与分析研究，对钻井船的船型论证具有实际意义。

本文应用基于三维零航速势流理论的AQWA海洋工程水动力分析工具，进行钻井船摇荡运动预报，并完成钻井船摇荡运动模型试验。在此基础上，提出钻井船摇荡运动衡准，结合短期预报理论，对相应海况下的作业适应性进行分析。通过计算对比无月池及不同尺度月池下的钻井船摇荡运动响应，分析月池对钻井船运动性能的影响。

1　钻井船摇荡运动预报分析理论

随着计算机技术的发展，三维势流理论日臻完善，在海洋工程结构物水动力分析领域应用广泛［4］。

1.1 三维势流理论基础

对于无航速浮体，流场扰动速度势为：

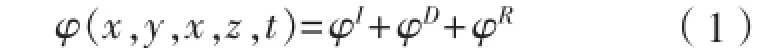
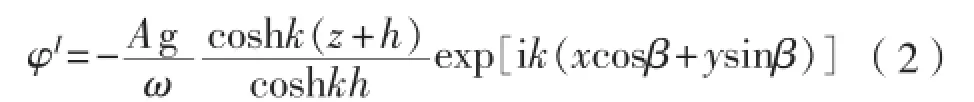
式中：、、分别为入射势、绕射势和辐射势。根据线性波浪理论，波浪入射势可表示为：式中：A为波幅，m；k为波数，rad/m；h为水深，m；g为重力加速度，m/s2；β为浪向与x轴正方向的夹角，°，规定β=180°为迎浪。

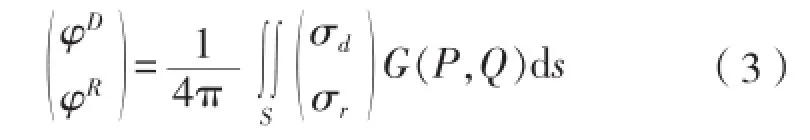
入射势、绕射势根据Green函数法求取：式中：S为物体边界，为分布于湿表面上的源强，为物面S上的动点，为场点。

根据速度势与Lagrange积分式（2）-式（4），即可获得流场压力分布。

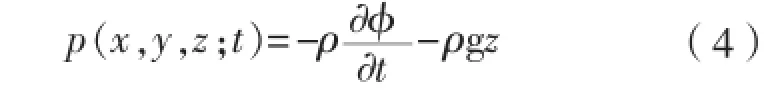
流体压力沿结构物表面积分，得到结构物所受到的总体流体作用力，包括波浪激励力、辐射力以及流体静回复力，其中辐射力通常用附加质量系数和辐射阻尼系数表征。因此，船体在频域下的一阶摇荡方程表达式为：式中：J和k为运动模态 （j=1～6，k=1～6）；xj为船体运动位移；mkj为船体质量；μkj为船体附加质量；λkj为船体阻尼系数；ckj为船体回复系数；Fwk为船体的波浪干扰力。

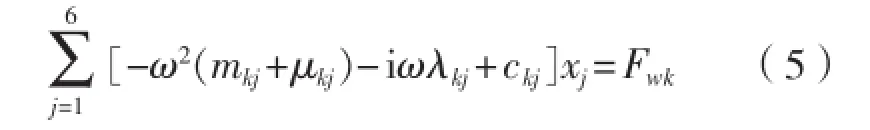
1.2 钻井船频域运动计算模型

将钻井船与月池内的流体视为一个体系中2个独立又相互影响的组成部分［5］。相对于钻井船而言，船体运动受到月池内流体运动的影响，如以月池内流体垂向运动为影响因素，建立钻井船运动方程为：式中：x8为月池内流体垂向运动位移；ak8、bk8分别为月池垂向运动引起的附加质量影响系数、阻尼影响系数。

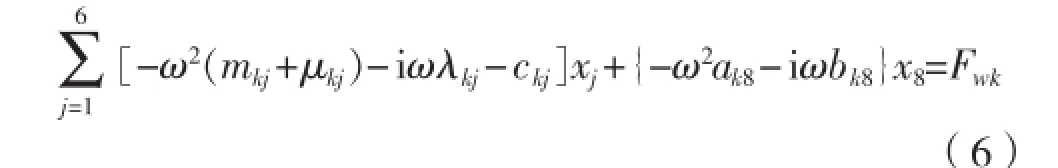
钻井船以及月池内流体体系的运动示意如下页图1所示。

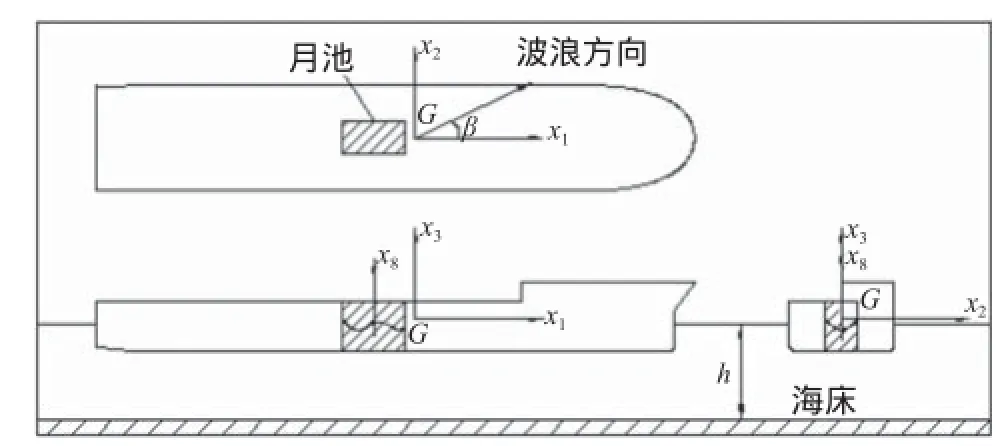
图1 体系运动示意图

月池内流体的绝对运动可分解为：式中：x3为月池内流体与船体一致的运动；x′为月池内流体与船体的相对运动。

钻井船运动预报过程中，由于月池运动x8未知且量级较小，因此视x8≈x3，式（6）可表示为：同理，计入月池六自由度运动影响的钻井船摇荡运动方程为：式中：akj、bkj分别为月池k自由度上的运动对钻井船j自由度上的附加质量影响系数、附加阻尼影响系数。

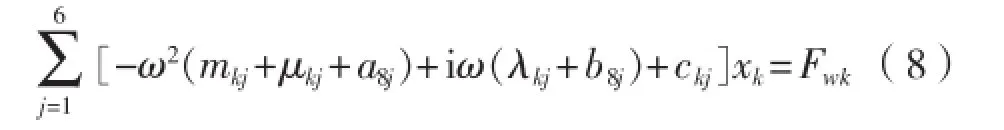
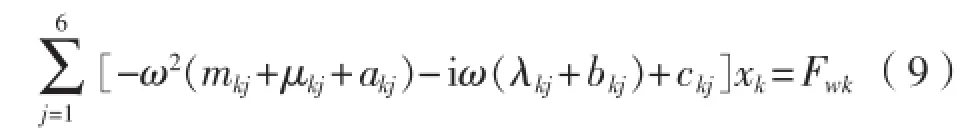
据A·B·Aalbers研究成果显示，ω＜0.3 rad/s范围内，附加质量影响系数、阻尼影响系数均可视为常数。因此，为简化预报过程且提高预报精度，AQWA数值计算过程中，将结合附加质量影响系数、阻尼影响系数、钻井船粘性阻尼系数进行水动力系数修正［6-8］。

1.3 摇荡运动短期预报理论

为了获得钻井船在随机波中的摇荡运动统计值，根据谱分析理论对钻井船摇荡运动幅度进行短期预报。主要过程为：

（1）摇荡运动幅频响应函数（RAO）。

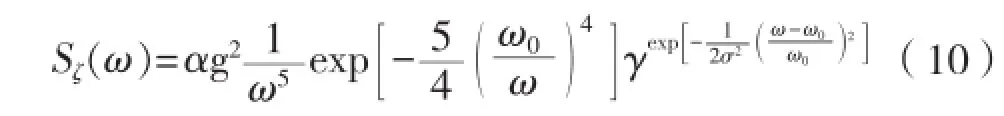
（2）波能谱密度函数：式中：ω0为谱峰频率；γ为谱峰升高因子；σ为谱峰形状参数；α为无因次常数。

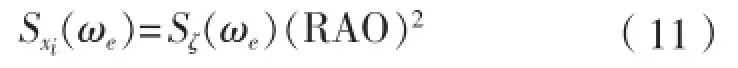
（4）摇荡运动位移单幅有义值：

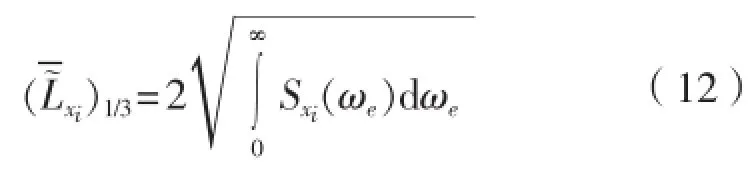
1.4 钻井船摇荡运动衡准

钻井船具有细长的船体外形且水线面积较大，在波浪中运动幅值较大，将可能影响海上正常钻井作业。因此，在船型设计阶段，需要结合摇荡运动衡准及运动幅值预报结果，对不同海况下的钻井船作业适应性进行分析。然而，目前尚无权威机构规定明确的钻井船摇荡运动衡准选取标准，这是钻井船作业适应性分析的技术瓶颈。

然而，钻井船是具有船体外形的海上钻井平台，本文在结合常规船舶耐波性要求及海洋平台作业特点基础上，提出钻井船作业过程中（安装防喷器）的摇动运动衡准如表1所示［9］。

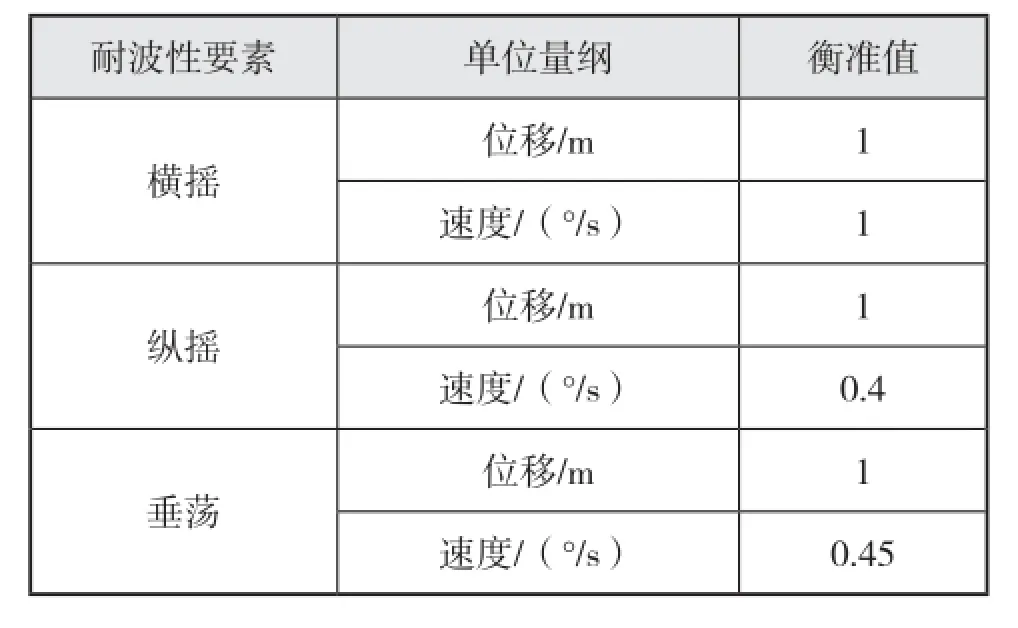
表1 钻井船摇荡运动衡准值

1.5 月池特性分析方法

由于月池结构贯穿船底，池内流体柱与外部海水相连，在波浪作用下，流体柱将产生“活塞”和“晃荡”两种不规则的振荡，影响流场压力分布。目前，关于月池的研究均停留在以模型试验和理论研究为主的自身特性研究。Faltinsen、Fukuda、Molin等人给出的月池流体振荡固有频率经验计算模型，Aalbers、Knott 和 Flower等人通过模型试验对月池的共振频率下的附加阻尼或附加质量进行研究。English、Park J J等人以减小航行阻力提高迁移速度为目标，对月池尺度进行优化设计［10］。

Molin通过推导月池内流体做活塞运动和晃荡运动时的速度势得到其固有频率计算公式如式（13）和式（14）所示。式中：d为月池吃水，m；l为月池长度，m；b 为月池宽度，m；g为重力加速度，m/s2。

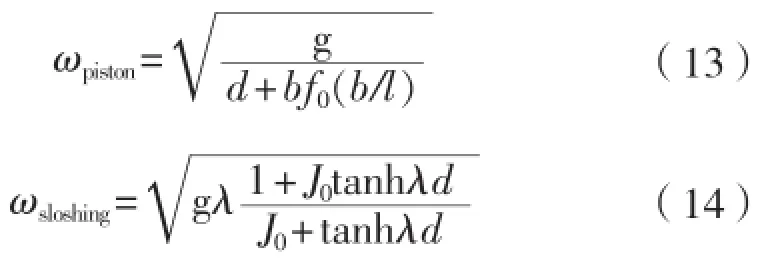
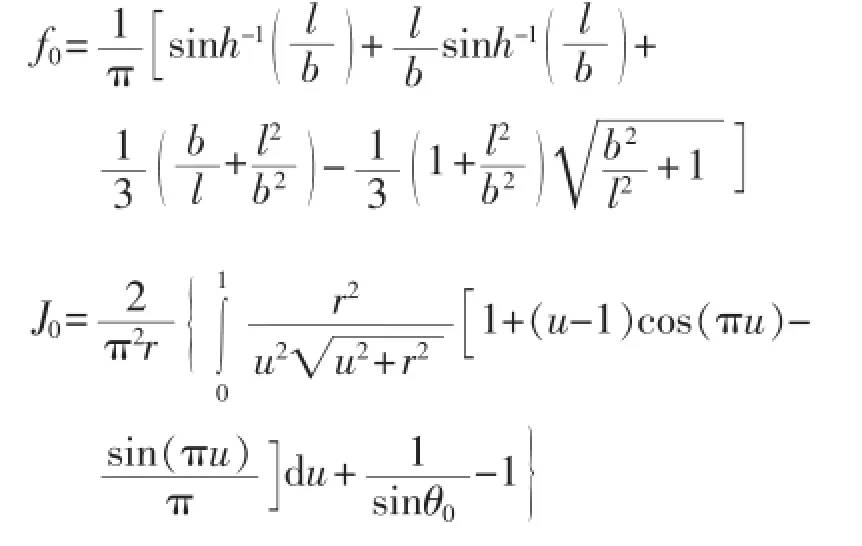
2　实例计算与分析

本文以1艘科研钻井船型为例，对该钻井船的运动响应进行预报并开展船模摇荡运动试验，在此基础上，分析指定海况下的摇荡运动适应性以及月池尺度对钻井船摇荡运动的影响。

2.1 数值计算模型

实例钻井船主要参数见表3。

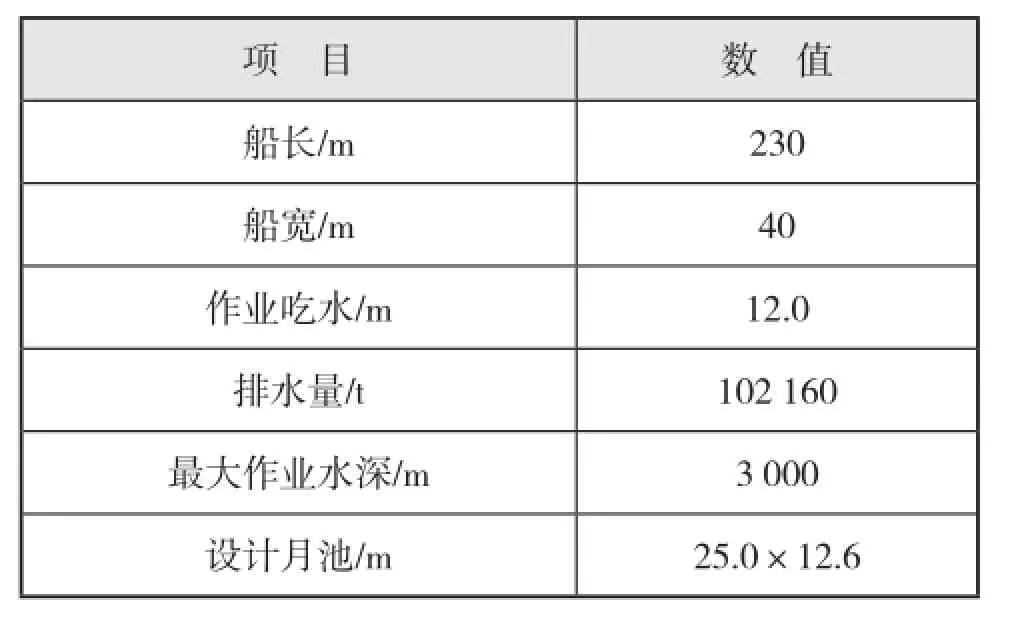
表3 钻井船主要参数

数值计算几何模型如图2所示。式中：h为船体吃水，m；S为月池剖面面积，m2；λ=π/l，r=b/l，tanθ0=r-1。

由Molin经验公式估算目标船型月池固有频率：活塞运动固有频率ωpiston=0.815 rad/s晃荡运动固有频率ωsloshing=1.147 rad/s

为分析月池的存在及其尺度对钻井船摇荡运动的影响，对不同尺度下的钻井船摇荡运动响应进行计算分析，月池尺度如表2所示［11］。

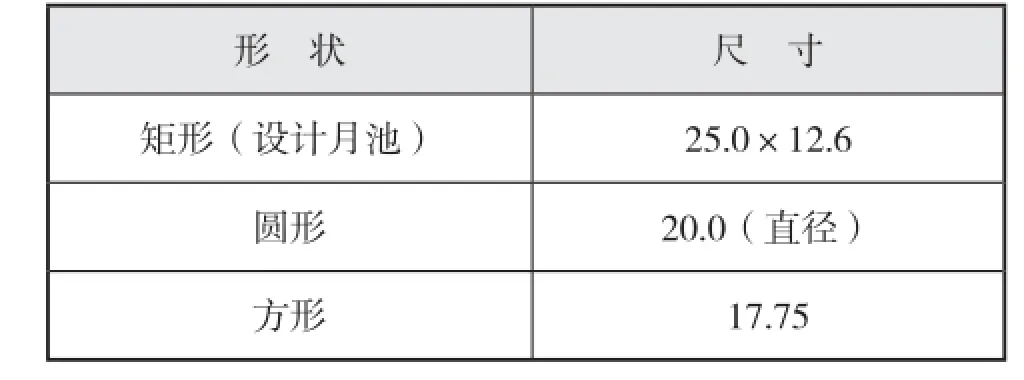
表2 月池尺度m

图2 钻井船几何模型

2.2 摇荡运动数值预报与船模试验

基于三维零航速势流理论，应用水动力分析工具AQWA，获得钻井船在规则波中的摇荡运动幅频响应。

下页图3表示不同浪向下的垂荡幅频响应，纵坐标为单位波幅的垂荡位移。

下页图4和图5分别表示不同浪向下的横摇、纵摇幅频响应，纵坐标表示单位波倾角的倾斜弧度。

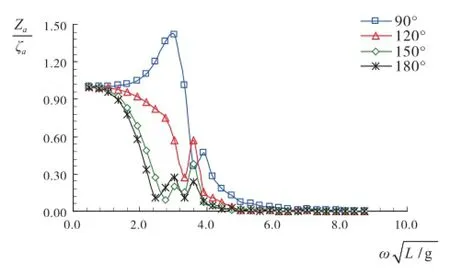
图3 垂荡运动幅频响应

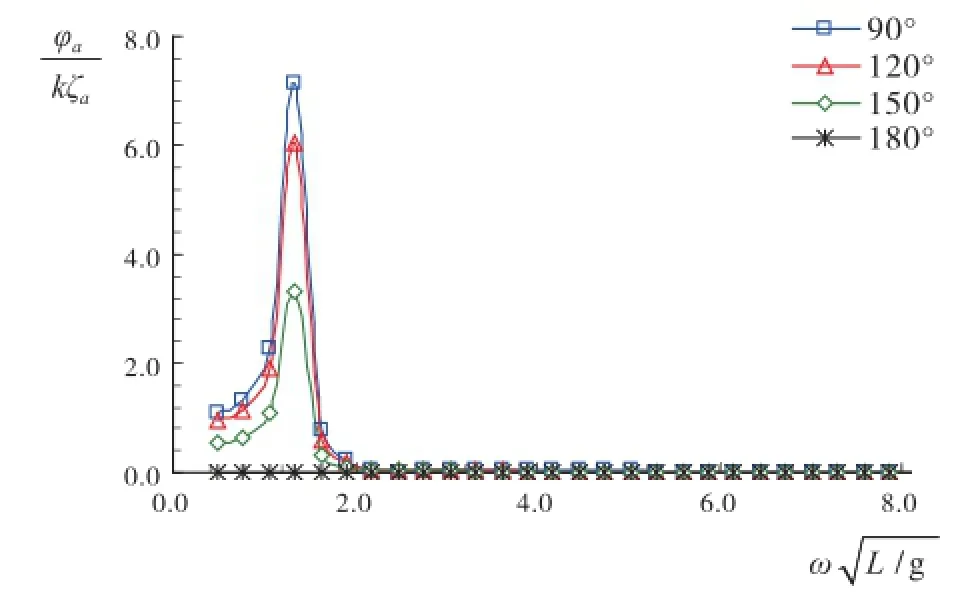
图4 横摇运动幅频响应

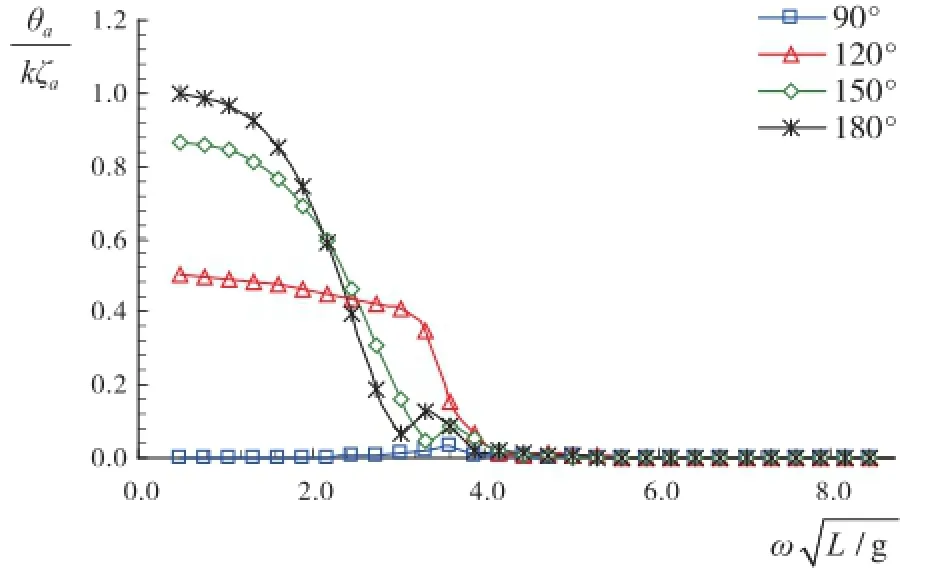
图5 纵摇运动幅频响应

图6 船模试验截图

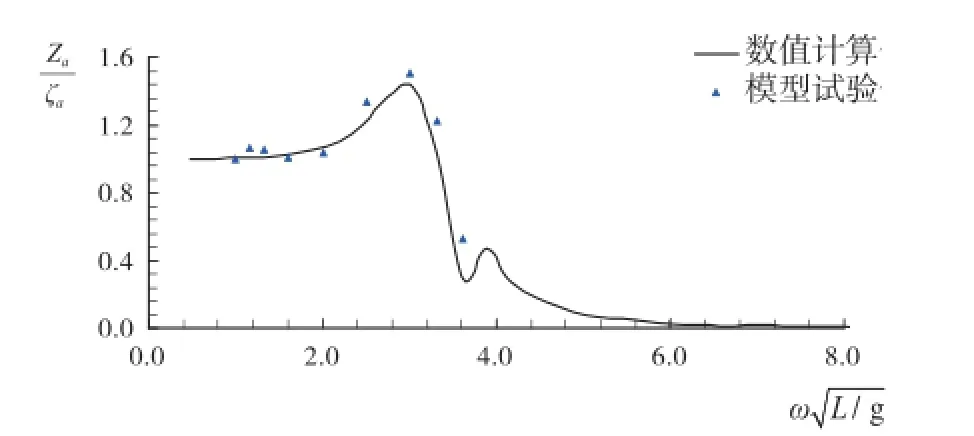
图7 垂荡运动响应（β=90°）

为了验证数值计算结果的有效性，开展该钻井船作业装载工况（作业吃水见表3）与典型浪向下的摇荡运动模型试验，浪向角β=180°时为正迎浪。图6为船模试验过程截图。

钻井船摇荡运动数值计算结果与模型试验结果如图7 -图9所示。数值计算值与模型试验值吻合度较好，验证了数值计算结果的有效性及数值计算方法的可靠性。

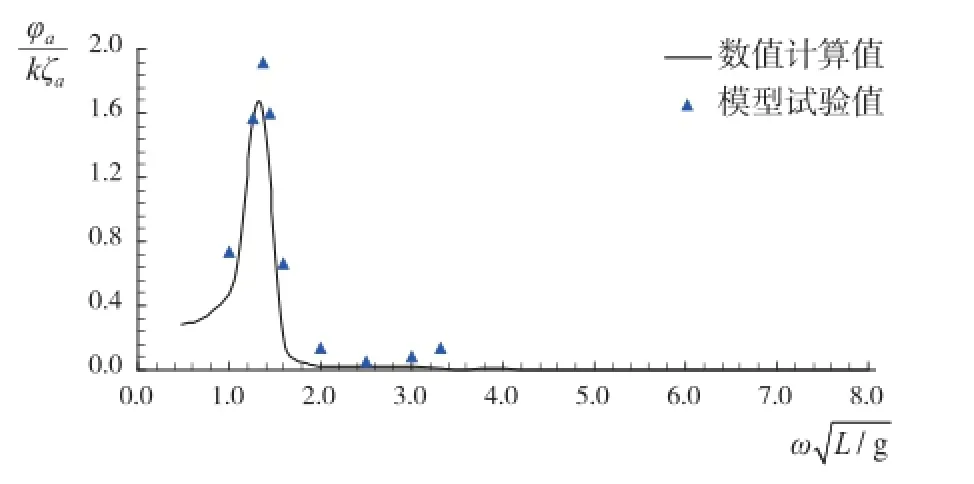
图8 横摇运动响应（β=165°）

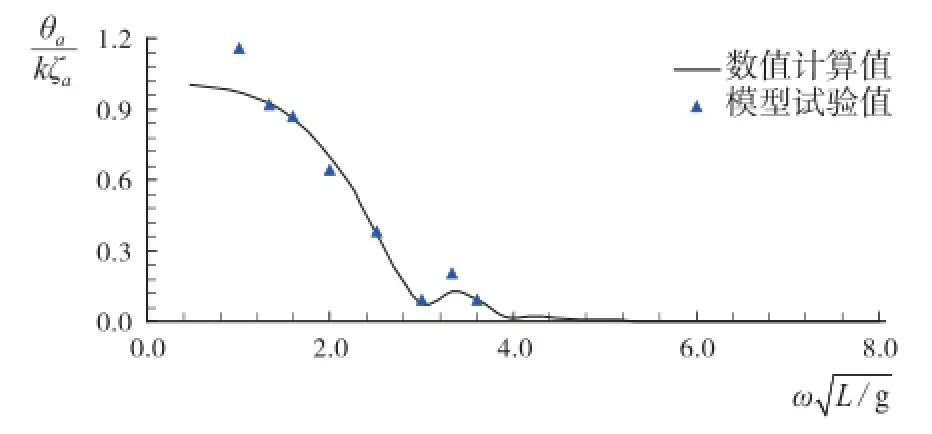
图9 纵摇运动响应（β=180°）

2.3 钻井船作业适应性分析

根据谱分析理论，对不规则波中的摇荡运动进行短期预报，并结合表1中的摇荡运动衡准值，分析该钻井船在相应海况下的作业适应性。

图10 -图12分别表示不同海况下的垂荡、横摇、纵摇位移以及对应的衡准限界线玫瑰图。

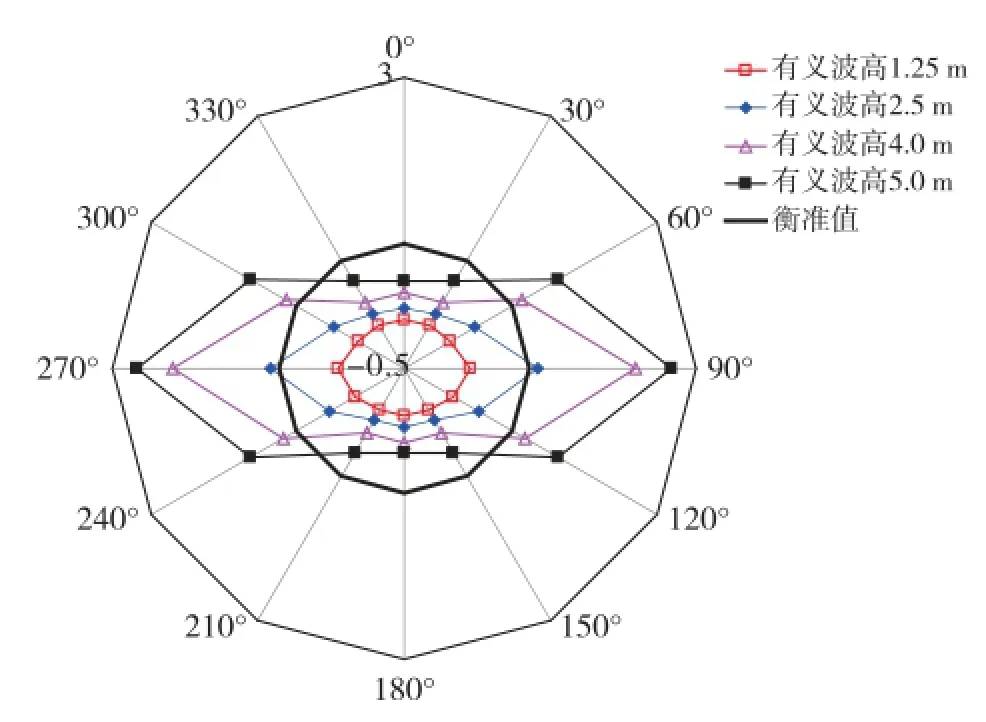
图10 垂荡运动位移玫瑰图

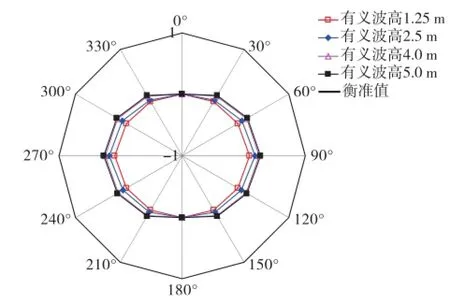
图11 横摇运动位移玫瑰图

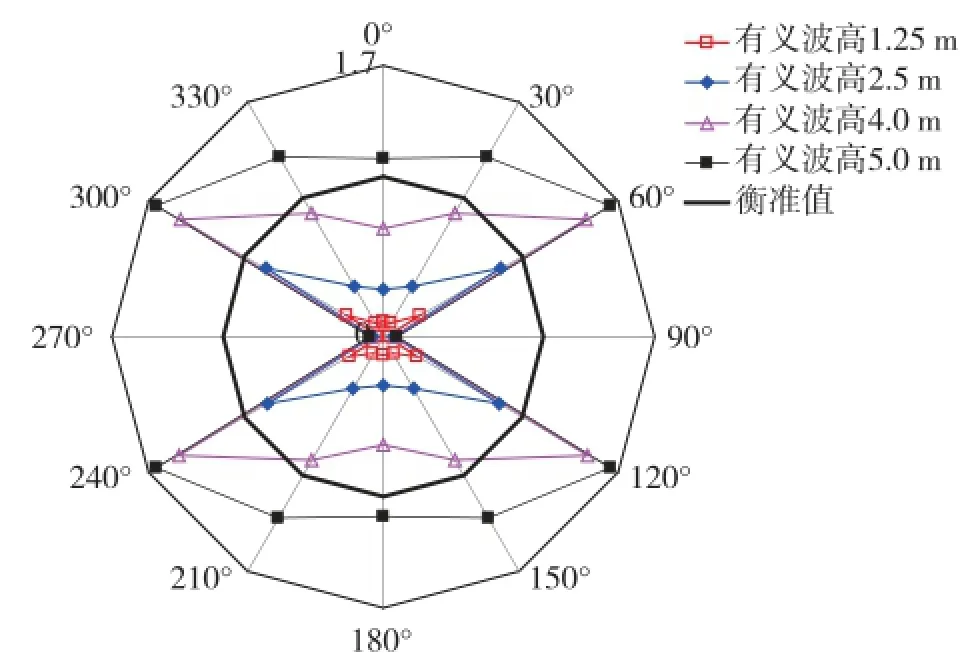
图12 纵摇运动位移玫瑰图

图13 -图15分别表示不同海况下的垂荡、横摇、纵摇速度以及对应的衡准限界线玫瑰图。

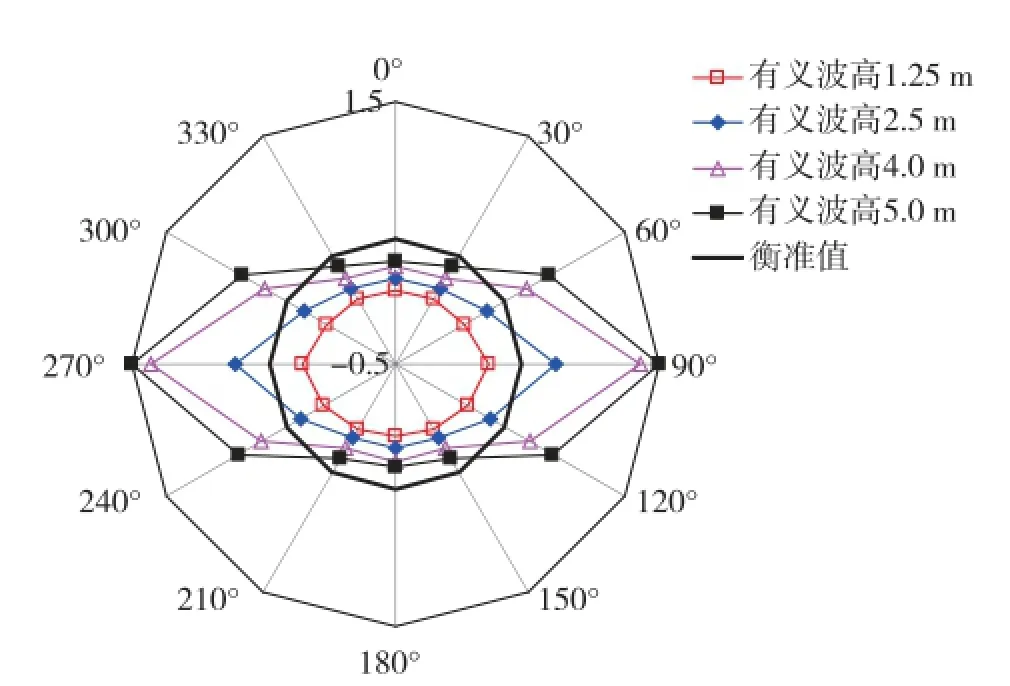
图13 垂荡运动速度玫瑰图

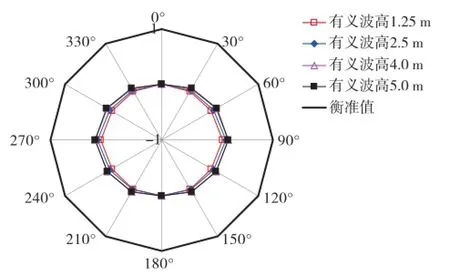
图14 横摇运动速度玫瑰图

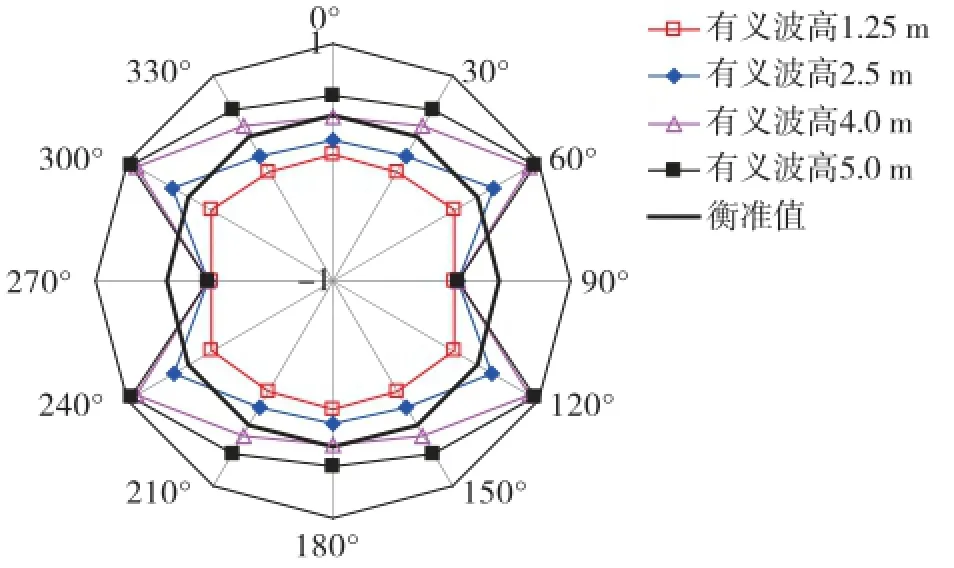
图15 纵摇运动速度玫瑰图

由图可知：若该钻井船采用锚泊定位系统，迎浪方向随机分布，则只有在有义波高h1/3=1.25 m的低海况下才能满足衡准值要求，具备良好的作业适应性。若钻井船采用动力定位系统，船首可控制在迎浪β=180°至首斜浪β=150°的范围内，则在有义波高上h1/3=5.0 m的高海况下，也能基本满足衡准要求，保持较好的作业适应性。由于该钻井船横摇固有周期T=21 s，波浪周期范围大多在15 s以下，因此，横摇频率响应与波浪能量谱存在峰值偏移，钻井船横摇运动缓慢且摇荡幅度小，不影响正常钻井作业。

2.4 月池对钻井船摇荡运动影响分析

建立不同尺度月池的钻井船几何模型，基于三维势流理论得到不同尺度月池下的钻井船垂荡、横摇、纵摇运动响应（β=135°）如图16 -图18所示。

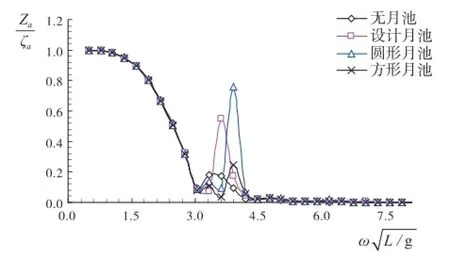
图16 垂荡运动响应

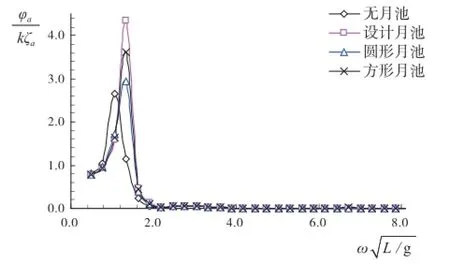
图17 横摇运动响应

由图16可知，在月池的“活塞”运动固有频率附近，钻井船垂向运动与月池内流体的活塞运动发生共振，钻井船垂荡运动曲线出现强烈振荡，且矩形月池和圆形月池的振荡现象最为剧烈。

由图17可知，月池的存在减小了钻井船的横摇固有周期，导致横摇更加剧烈，且明显增大横摇峰值，矩形月池的增大幅度最为显著。

由图18可知，月池的存在对纵摇响应无影响。

基于以上分析可知，月池结构对钻井船垂荡和横摇两个方向上的运动造成影响，垂荡方向上易于发生共振现象，横摇方向上表现为增大横摇幅度。基于谱分析原理，对不同尺度下钻井船横摇运动进行短期预报如图19所示。

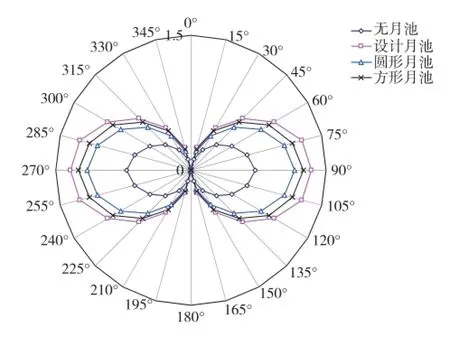
图19 横摇运动短期预报值（h1/3=9.0 m）

3　结　论

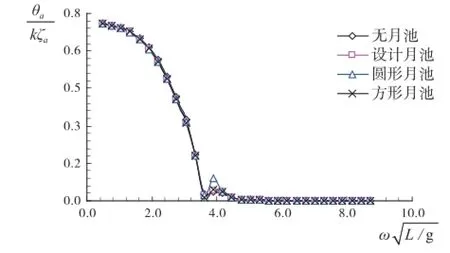
图18 纵摇运动响应

通过以上计算与分析，得出如下结论：

（1）基于AQWA的钻井船摇荡运动数值预报方法较为可靠，鉴于月池存在引起型值和水动力系数的修正，获得的钻井船在波浪中的运动响应与模型试验结果相吻合，从而验证了预报方法的可靠性。

（2）保持船首处于迎浪方向有利于钻井船在恶劣海况下也能保持良好作业适应性，且钻井船横摇方向运动缓慢、幅度又小，对正常作业并无不良影响。

（3）月池对钻井船垂荡和横摇两个方向的运动造成不良影响。由于月池内流体柱的“活塞”振荡，钻井船垂荡方向上易于发生共振现象，横摇方向上表现为横摇幅度增大，并且矩形月池的增大效果最为明显，其次为方形月池和圆形月池。

［ 1 ］ Anon. Floating into Ultra-Deepwater［EB/OL］.［2014-03-20］. http://www.hellenicshippingnews.com/07be9lal-7e63-4b44-9807-b4e4b26a8573/.

［ 2 ］ 孙采微.深水钻井船水动力性能研究［D］.上海：上海交通大学，2013：2-7.

［ 3 ］ Molin B. On the piston and sloshing modes in moonpools［J］. Journal of Fluid Mechanics，2001（1）： 27-50.

［ 4 ］刘应中，缪国平.船舶在波浪中的运动理论［M］.上海：上海交通大学出版社，1987.

［ 5 ］Aalbers A B. The water motion in moonpool［J］.Ocean Engineering， 1984（6）：557-579.

［ 6 ］ Cueva M， Malta E B， Nishimoto K， et al. Estimation of Damping Coefficients of Moonpools for Monocolumn Type Units［C］//Proc.of OMAE’05， 24th International Conference on Offshore Mechanics and Arctic Engineering. Greece： OMAE， 2005.

［ 7 ］ Maisondieu， Jouëtte D C， Kimmoun C， et al. Numerical and Experimental Evaluation of the Viscous Damping in a Wellbay［C］ //Proc.of OMAE’04， 23rd International Conference on Offshore Mechanics and Arctic Engineering. Canada： OMAE，2004.

［ 8 ］ Fukda K. Behavior of water in vertical well with bottom opening of ship and its effect on ship motions ［J］. Journal of the Society of Naval Architects of Japan， 1977， 141：107-122.

［ 9 ］ Journée J M J，Massie W W. Offshore Hydromechanics［M］. Delft University of Technology. Delft， 2001.

［10］ Park J J， Kim M S. Development of Design Technologies for Optimum Moonpool Shapes of Drillship ［C］// Proc. of OMAE’07， 26th International Conference on Offshore Mechanics and Arctic Engineering. USA： OMAE， 2005.

［11］ Fung D P K. Added Mass and Damping of Circular Moonpools［C］// Proceedings of the 6th International Offshore and Polar Engineering Conference. USA：ISOPE， 1996.

Motion performance of drillship with moonpool

ZHANG Xiao-yu1HU Kai-ye2ZHOU Wen-wen2
(1. Ocean Engineering Equipment Research Institute of CNPC Bohai Equipment Research Institute, Panjin 124010, China; 2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Great stability is demanded for a dillship during the off shore drilling operation. However， the irregular oscillation of the fl uid cylinder of the moonpool and the elongated hull shape have adverse eff ect on the motion performance of the drillship， which may limit the drillship operation adaptability in rough sea states. The oscillation of a drillship with a moonpool is predicted by the three-dimension potential theory， and the results are validated by the ship model tests in order to put forward the criterion value of the drillship oscillation. On this basis， it analyzes the drillship operation adaptability in deep sea and the infl uence of the scale and shape of the moonpool on the motion performance of the drillship.

drillship； motion prediction； moonpool

U661.1

A

1001-9855（2016）01-0029-08

中国石油天然气集团公司攻关课题（2011B-1064）

2015-01-30；

2015-11-18

张晓宇（1972-），男，硕士，高级工程师，研究方向：海工装备。胡开业（1980-），男，博士，讲师，研究方向：水动力性能分析。周雯雯（1989-），女，硕士，研究方向：船舶工程。