改进量子粒子群算法在光伏最大功率点中应用

安徽农业大学信息与计算机学院　农业部农业物联网技术集成与应用重点实验室　朱娟娟　王　伟　乔　焰　王月康　周海鹏　李　旸

改进量子粒子群算法在光伏最大功率点中应用

安徽农业大学信息与计算机学院农业部农业物联网技术集成与应用重点实验室朱娟娟王伟乔焰王月康周海鹏李旸

光伏阵列的 P-U 特性曲线在局部遮阴环境（如树木遮挡、云层变化等）下呈现多个极值点，这会导致传统的最大功率点跟踪（maximum power point tracking， MPPT）算法失效。基于此提出了一种改进量子粒子群算法的最大功率点跟踪控制方法。该算法采用量子δ势阱模型，同时引入锦标赛选择机制和随机加权平均最好位置操作，提高搜索效率的同时保持了种群多样性。在 MATLAB 中建立基本粒子群、量子粒子群、改进量子粒子群三种算法仿真研究。结果表明，对比其他两种粒子群算法，该算法能更为精准的跟踪光伏阵列最大功率点，有效地提高了光伏阵列的输出效率。

光伏系统；局部遮阴；最大功率点跟踪；粒子群优化算法

0.引言

随着全球能源危机的加剧以及人们对低碳环保生活理念的渴求，可再生能源的开拓与探索早已成为研究的重点领域。在所有可再生能源中，太阳能具有取之不尽、用之不竭、能量巨大、安全无污染等诸多优点，堪称理想能源。作为太阳能利用的主要形式，光伏发电的开发与设计一直是全世界的热门方向［1］。由于单体光伏组件发电容量有限，在实际应用中都是由多个单体光伏组件串联形成光伏阵列。当光伏阵列中各单体组件均匀接收太阳能辐射时，其输出功率呈单峰状曲线。然而，受现实客观因素诸如树木遮挡、云层变化等影响，光伏阵列各个部分接收光照强度不均等时，整个光伏阵列的输出功率会呈现多个峰值点。传统的最大功率点跟踪算法在解决这类多峰极值点时会失效［2］，不能快速准确的跟踪到最大功率点，造成太阳能发电系统输出功率的损耗。针对光伏阵列的MPPT优化问题，群体智能算法在这方面的研究越来越普及。而其中，粒子群算法以其实现容易、参数少、收敛快等优点尤其受到广泛重视。文献［3］采用粒子群及其改进算法搜索局部遮阴情况下的最大功率点，均取得了不错的效果。但粒子群算法本身存在着“早熟”收敛、常仅获得局部最优解［4］等缺点。

为了更快速准确的获得局部遮阴情况下的光伏阵列最大功率点，提高光伏阵列输出效率，并克服标准粒子群算法群体智能程度低，协同搜索能力差［5］等缺陷，本文提出一种改进的量子粒子群（MQPSO）算法，并同基本粒子群（PSO）、量子粒子群（QPSO）两种算法在MPPT中的应用进行对比仿真实验，验证本算法的有效性。

1.相关工作

1.1基于MATLAB的光伏电池通用数学模型

本文中，光伏电池采用工程模型［6］，光伏电池I-V 方程简化如下式：

在实际应用环境中，这些标准参数需要根据光照强度和温度进行补偿修正，令：

电流修正值为：

电压修正值为：

那么，光伏阵列（由K块单体光伏电池串联）的MPPT问题目标函数为：

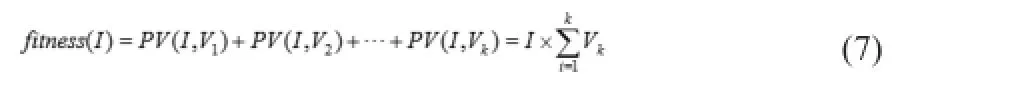
1.2量子粒子群算法描述

以孙俊博士等代表的国内学者从量子力学的角度出发，利用量子侧不转原理来描述粒子的运动状态，建立了一种新的PSO（Particle Swarm Optimization， PSO）算法模型，该模型是以δ势阱为基础，认为粒子具有量子的行为，并据此提出了量子粒子群算法［8］。在量子空间中，粒子的聚集性通过在粒子运动中心存在的Pi点吸引势产生的束缚态来描述，而处于量子束缚态的粒子可以以一定的概率密度出现在可行解的任何点［9］，因此搜索过程中的粒子每个迭代步的搜索空间可以覆盖整个可行解空间，算法的全局搜索性能优于标准PSO算法，且群体智能化程度高，协同搜索能力强［5］。

设搜索空间为j维，则基于δ势阱模型的粒子位置更新公式如式（8）-（11）所示：

QPSO 算法详细描述如下：

Initialize X； % 在可行解空间中初始化种群粒子位置

for t = 1: t_max % 循环开始

γ= （1.0 - 0.5）*（t_max - t）/t_max + 0.5% 收缩-扩张系数γ从1.0到0.5线性递减

mbest=mean（X） % 计算粒子种群的平均最好位置

for i = 1 to 种群规模 N

if f （Xi） ＞ f （Pi） then Pi= Xi% P保存种群个体最优值

Pg= max （Pi） % Pg保存群体最优值

for j = 1 to 粒子维度 D

u = rand （0， 1） v= rand （0， 1）

p = u*Pid+（1-u） * Pg% 局部吸引子坐标公式

if v ＞= 0.5 % 根据位置更新公式计算粒子新位置

Xid= p+β*abs（mbest-Xid）*ln（1/v）

else

Xid= p-β*abs（mbest-Xid）*ln（1/v）

将更新后的粒子位置限制在搜索范围中；

如果达到指定的迭代次数或满足结束条件则算法结束，否则进入下一次迭代循环。

2.基于MQPSO算法在光伏系统最大功率点跟踪中的应用

2.1算法基本思想

QPSO算法的思想来源于量子力学和基本PSO模型。它具有较强的全局收敛性，控制参数更少，寻优能力更强。但是，与其他进化算法一样，也会遇到局部极值的问题，算法后期种群多样性减少。

为此，本文将从两个方面对QPSO算法进行改进，避免QPSO算法后期陷入局部最优值和多样性减少的问题。一是从式（9）中的Pg入手，采用锦标赛选择法［10］来决定Pg的取值；二是修改式（11）中的mbestt取种群粒子平均位置的做法，利用随机性原理，为每个粒子产生一个随机贡献率，得到随机加权平均最优位置，记为avgmbestt［11］。

2.2改进部分概述

2.2.1QPSO算法中引入锦标赛选择操作

在锦标赛选择法中，首先随机产生一定数目的个体，称为竞赛规模；其次将最优个体选做父个体。重复前面两步，直至完成个体的选择。在本文中，竞赛规模设为1，每次随机的从种群中挑选出一个个体k，根据目标函数计算其值，并与当前粒子的目标函数值相比较。如果好于当前粒子的目标函数值，则吸引子Pi由Pi和Pk共同决定；否则，Pi由Pi和Pg决定。其伪代码如下：

Selection_T:

k=ceil×（N，1）； % 从种群N个粒子随机产生一个

if f （Pk） ＞ f （Pi） then T= Pk% 选择操作

else T=Pg

end if % 选择操作结束

Return T

通过选择操作选出T后，式（9）变为：

2.2.2QPSO算法中引入随机加权平均最优位置

QPSO算法中的平均最优位置mbestt是对当前群体的每个粒子位置均值得到，即每个粒子的位置对mbestt的贡献全部一致。这里将对mbestt进行修改，利用随机性原理，为粒子种群产生一个随机贡献度序列，与当前粒子的位置共同得到随机加权平均最优位置avgmbestt。具体做法如下：

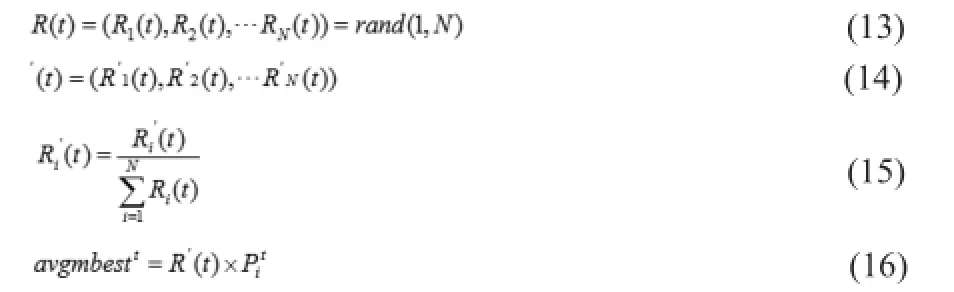
2.3算法流程

1） 设置光伏阵列的MPPT模型参数，利用算法初始化产生Vm附近的D维电压粒子，并根据输入S、T及目标函数式（7）计算对应粒子的输出功率；

2） 初始化每个粒子的个体最优Pbest、群体最优Pg以及Pk；

3） 收缩扩张系数γ随迭代次数从1.0到0.5线性减小；

4） 根据式（15）计算种群的随机加权平均最好位置avgmbestt，并利用式（16）更新每个粒子的位置（须限制在（0，Voc）位置范围内），并根据目标函数计算每个粒子更新后的输出值；

5） 将每个粒子更新位置后的覆盖率与Pbest对应的覆盖率相比较，如果前者较大，则更新Pbest；

6） 将种群中的每个粒子的个体最优Pbest对应的覆盖率与Pg对应的覆盖率相比较，如果前者较大，则更新Pg；

7） 如果循环未达到预设最大迭代次数，则返回2）；否则算法结束，并返回群体最优分布。

3.仿真实验

3.1MATLAB仿真及结果

根据1.1节光伏电池的数学模型，电池板的固有参数如下：

对两块串联的电池板的外界输入参数设置如下：

根据上述设置，利用MATLAB可以得到光伏阵列的输出功率-电压之间的双峰特性曲线，如图1所示。将MQPSO算法应用到MPPT的寻优当中，所得结果如图2所示（图2中Pg第一列数值表示最大功率点时的电流，第二列数值表示最大功率值）。

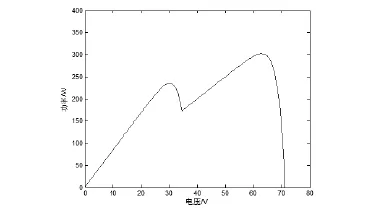
图1　光伏阵列的输出特性

图2　改进QPSO算法寻优结果

从图1可以看到，P-V曲线有两个极值点，其中最大功率点输出功率值为301.14W，对应的最大功率点电压为63.0V。图2给出改进的QPSO算法寻优结果，最大功率点的输出功率为299.5212W，对应的最大功率点的电流为4.7877A，从而得到最大功率点的电压为62.56V；这同理论最大功率值301.14W及最大功率点电压63.0V相比，相对误差很小，算法寻优结果很精确。算法寻优耗时0.0853s，说明此方法收敛速度快，而且多次运行也未陷入局部最优解，由此可见改进之后的QPSO算法能快速准确的跟踪到光伏阵列的最大功率点。

3.2 三种算法的实验结果对比分析

为了更好的验证本算法性能，选择基本粒子群（PSO）、量子粒子群（QPSO）及改进QPSO三种粒子群算法做对比实验。为了更好的评价算法，对3种算法分别进行20次独立的优化试验，比较每种算法在输出功率、耗时两个性能指标上的优劣，每种算法的性能指标数据如表1所示。

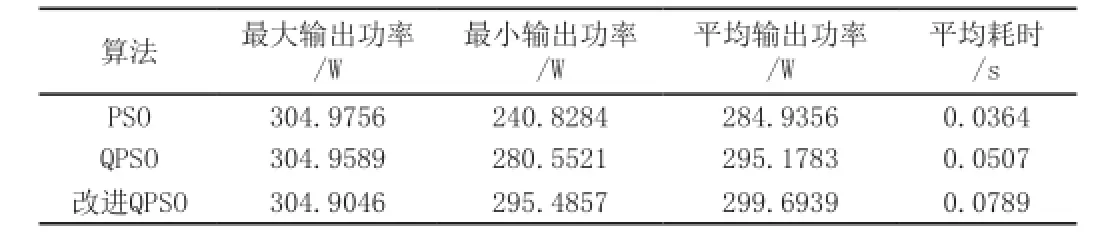
表1　算法运行20次结果对比

从表1数据可以看出：在平均输出功率方面，改进后的QPSO算法测试结果与图1中的理论最大功率值299.8W最接近，相对误差最小，20次测试平均值为299.6939W，改进QPSO、QPSO、PSO算法的相对误差分别为7.43‰、1.98%、5.38%；同时，改进QPSO算法寻优的最大最小输出功率与理论值的相对误差均优于QPSO及PSO算法。在平均耗时方面，改进的QPSO算法的运行时间最长，20次测试平均值为0.0789s，比QPSO、PSO算法延迟了28.2ms、42.5ms。

综合上述可知，改进的QPSO算法相对于其他两种粒子群算法在输出功率精度方面优势明显，寻优结果更为接近光伏阵列的理论最大输出功率值，多次运行也未陷入早熟收敛。虽然算法耗时相对增加了，但是延迟时间在10-2数量级内，对于实际部署安装环境中的每10分钟测量一次光照强度和温度变化来说，寻优时间对光伏阵列的影响可忽略不计。

4.结语

鉴于MPPT问题在光伏发电系统研究中的重要性，以光伏阵列的输出功率为优化目标，通过对QPSO算法做锦标赛制选择操作和随机加权平均最优位置的改进，加强了算法的随机选择性，在算法后期避免了种群多样性的减少，增强了算法挣脱局部极值点约束的能力。仿真结果表明，相对于其他2种粒子群算法，改进QPSO算法提高了MPPT的寻优精度。

［1］胡云岩，张瑞英，王军.中国太阳能光伏发电的发展现状及前景［J］.河北科技大学学报，2014（1）：69-72.

［2］周林，武剑，栗秋华等.光伏阵列最大功率点跟踪控制方法综述［J］.高电压技术，2008（6）：1145-1154.

［3］廉小亲，赵瑾，张晓力等.APSO算法在光伏阵列MPPT追踪器中的应用［J］.电源技术，2014（10）：1836-1838+1964.

［4］赫然，王永吉，王青等.一种改进的自适应逃逸微粒群算法及实验分析［J］.软件学报，2005，16（12）：2036-2044.

［5］孙俊.量子行为粒子群优化算法研究［D］.无锡：江南大学，2009.

［6］高金辉，邢倩，马高峰.光伏电池新型仿真模型及MPPT控制器的研究［J］.电测与仪表，2014（17）：107-111.

［7］Yusof Y，Sayuti S H，Abdul Latif M，et al.Modeling and simulation of maximum power point tracker for photovoltaic system［C］//Power and Energy Conference， 2004. PECon 2004.Proceedings.National.IEEE，2004：88-93.

［8］Sun J，Feng B，Xu W.Particle swarm optimization with particles having quantum behavior［C］//Congress on Evolutionary Computation.2004.

［9］孙俊，方伟，吴小俊等.量子行为粒子群优化：原理及其应用［M］.第1版 北京：清华大学出版社，2011.

［10］龙海侠，须文波，王小根等.基于选择操作的量子粒子群算法［J］.控制与决策，2010（10）：1499-1506.

［11］潘大志，刘志斌.量子粒子群算法的改进实现［J］.计算机工程与应用，2013（10）：25-27.

朱娟娟（1991—），女，安徽肥东人，硕士研究生，主要从事计算机应用技术、智能农业信息技术方面的研究。

国家自然科学基金项目National Natural Science Foundation of China （61402013），省科技攻关计划 （1301b042008）。