正交试验法在混凝土配合比设计中的应用
2016-10-24吴小锋黄小玲
吴小锋黄小玲
(1东莞市虎门港混凝土有限公司;2东莞华润水泥厂有限公司)
正交试验法在混凝土配合比设计中的应用
吴小锋1黄小玲2
(1东莞市虎门港混凝土有限公司;2东莞华润水泥厂有限公司)
本文尝试用正交试验设计通过较少的试验,运用数据分析方法来确定混凝土配合比中最佳的外加剂掺量、掺合料掺量及机制砂替代天然砂的合适的替代率。
正交试验;混凝土配合比;方差分析
1 前言
随着混凝土技术的不断发展,用于混凝土中的掺合料的种类也不断增多,各种混凝土外加剂更是层出不穷,再加上因天然砂资源越来越匮乏,各种人工砂也逐渐应用到混凝土的生产中。混凝土中的各种材料的搭配对混凝土性能的影响也越来越复杂,已经不能单凭经验就诸多因素对混凝土性能的影响进行准确的评估。但是如果对各种因素都进行试验,最大的问题就是试验次数太多,浪费很多人力和物力。例如,如果有四个因素对产品质量有影响,每个因素取三个不同水平进行比较,那么就需要进行34=81次试验。因此,有必要进行试验设计,通过较少的试验次数获得较多的信息,并通过数据分析来选择各因素的最佳水平,从而达到合理利用资源,节约成本并保证产品质量的目的。正交试验设计正是其中一种常用的方法。
2 正交设计试验原理
正交试验设计最早由日本统计学家田口玄一提出,称为国际标准型(田口型)正交试验法,是利用正交表来安排和分析多因素试验的一种设计方法[1]。它是在试验因素的全部组合中,选出有代表性的水平组合进行试验,通过对这部分试验结果的分析,了解全面试验的情况,找出最优的组合。如果把所有的试验集合看作一个立体空间,正交试验所选的试验在空间中具有“均匀分散,整齐可比”的特点。正交试验设计分无交互作用正交试验和有交互作用正交试验,本文只考虑无交互作用正交试验。
3 实验材料及方案设计
我们分析的试验因素有三种,分别是磨细灰的掺入量(因素A)、外加剂的掺量(因素B)还有机制砂占总砂的百分比(因素C)。为了使试验更简单而且有可比性,我们采用固定水胶比,固定总胶凝材料用量和固定砂率进行试验。水泥及掺合料的总量保持不变,掺合料为矿渣粉和磨细灰。主要考察的性能标准有三个方面:混凝土拌合物的流动度、坍落度损失和混凝土试块抗压强度。
3.1实验材料
⑴水泥:采用P·O42.5R水泥,物理性能见表1。

表1 水泥物理性能指标
⑵矿渣粉:S95级矿渣粉,比表面积448m2/kg,7d活性78%,28d活性104%。
⑶粉煤灰:II级复合磨细灰,45μm筛余14.2%,需水量比102%,7d活性指数64%,28d活性指数68%。
⑷细骨料:水洗砂,细度模数2.5;机制砂,细度模数3.0,石粉含量6.2%。
⑸粗骨料:石子,5~25mm连续级配。
⑹减水剂:聚羧酸高效减水剂(缓凝型)减水率23.2%。
3.2正交设计方案
⑴因素水平表(表2)
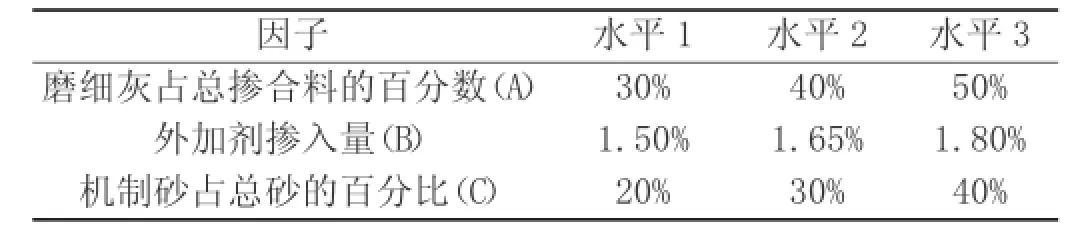
表2 因素水平
⑵正交设计表
根据因素的水平数采用正交设计表L9(34)(表3)。
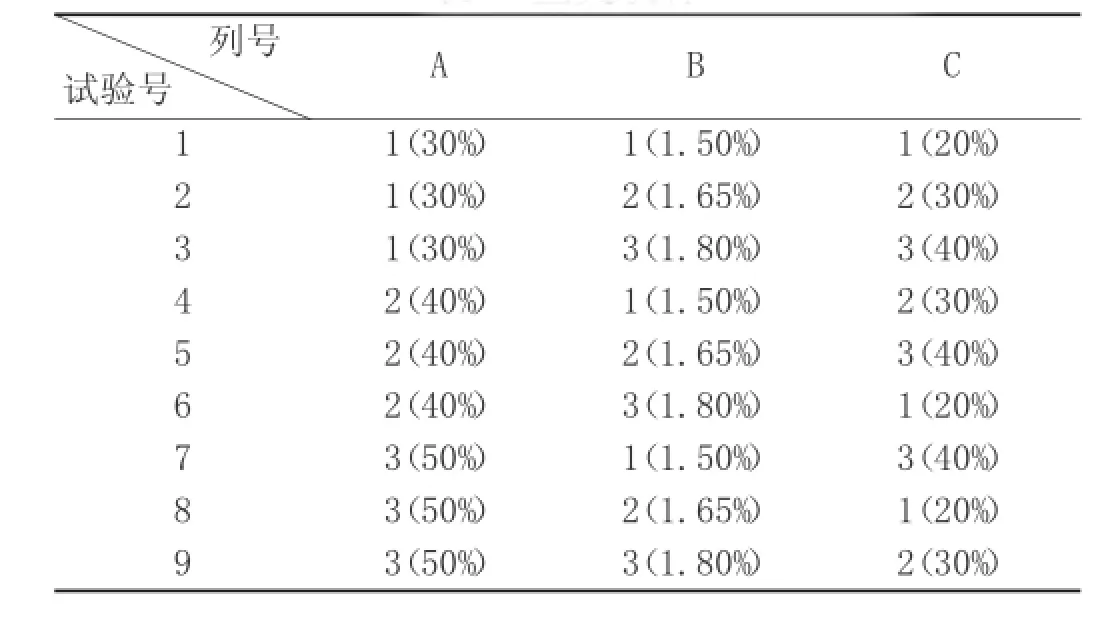
表3 正交设计
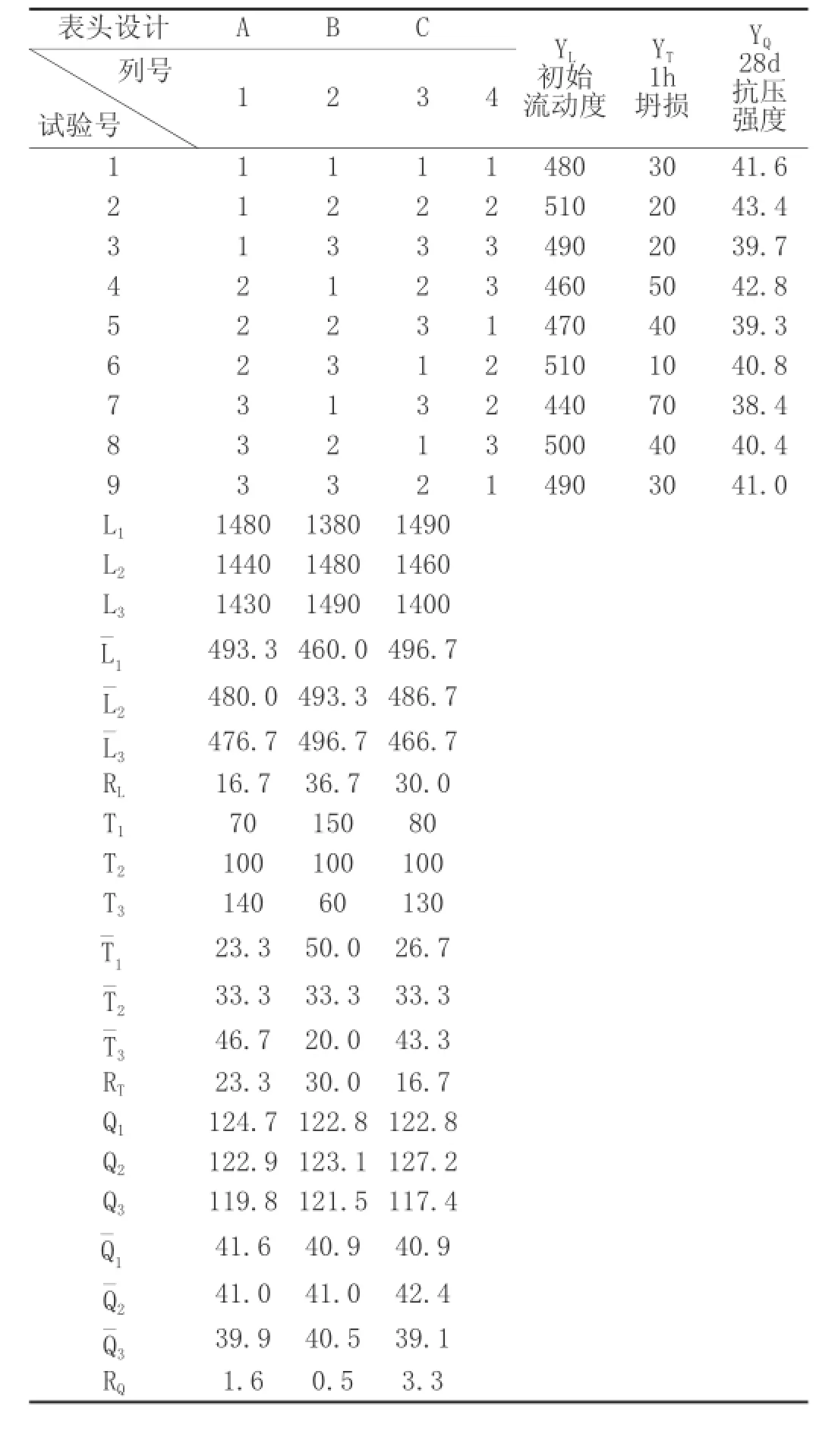
表4 直观分析计算
4 试验结果及分析
4.1直观分析(表4)
表4中L代表混凝土拌合物初始流动度,L1代表该因素所有水平为1的试验结果之和,L¯1为L1/3(以此类推),值较大说明流动度越好;T代表1小时坍落度损失,结果越小说明1小时坍落度损失越小;Q代表混凝土试块28d抗压强度,值越大说明抗压强度越高。R代表极差,它反映了各因素不同水平对应的试验结果均值的最大值与最小值之差,值越大说明该因素对指标的影响越大。
从表4可以看出,磨细灰掺量在水平1,也就是掺量占掺合料的30%时,混凝土拌合物的流动度最大;外加剂掺量在水平3,也就是掺量为1.8%时,混凝土拌合物流动度最大;机制砂占总砂的百分比在水平1,也就是替代率为20%时,混凝土流动度最大。从上述分析可以得出结论:混凝土流动度最佳时各因素的组合应该为A1+B3+C1,也就是磨细灰掺量为30%,外加剂掺量为1.8%,机制砂掺为20%时混凝土流动性最好。这一结论与我们所累积的经验一致。从各因素的极差可以看出,三种因素对混凝土拌合物的流动度均有一定的影响,但是以外加剂的掺量影响最大,其次是机制砂占总砂的百分比,而磨细灰的掺量影响较前两者要小。
各因素对混凝土拌合物1小时坍损及强度的影响可以按以上的思路去分析并得出结论,混凝土拌合物坍损较小的组合是A1+B3+C1,外加剂掺量对其影响最大,其次是磨细灰的掺量,机制砂占总砂的百分比对其影响略小。混凝土28d抗压强度较大的组合是A1+B2+C2,且机制砂的掺量对强度的影响较大,磨细灰的掺量影响较小,由于我们试验时是用固定水胶比,所以外加剂掺量在一定的范围内对强度几乎没有影响。
4.2方差分析
⑴方差分析计算表(表5)。
⑵方差分析表(表6)。
对于初始流动度,由于FA等于7.0,小于F0.9(2,2)=9.0,故因素A在显著性水平0.1上不显著,FB和FC大于F0.95(2,2)=19.0,故因素B和因素C在显著性水平0.05上是显著的。
同样的道理,对于1小时坍损,因素A、B、C均在显著性水平0.05上是显著的;对于28d抗压强度,因素A和因素C在显著性水平0.05上是显著的,因素B在显著性水平0.1上不显著。
⑶最佳组合的选择
对显著因素应该选择其最好的水平,因为其水平变化会造成指标的显著不同,而对不显著因子可以任意选
择水平,实际中往往根据成本的高低来选择。如果综合考虑上述三个性能指标,最佳的因素组合应该为A1+B3+C1。即磨细灰掺量占掺合量总量20%,外加剂掺量1.8%,机制砂占总砂的20%。但是,综合考虑到混凝土的强度、和易性及生产成本,在强度达到设计要求的基础之上,结合混凝土拌合物的和易性及生产成本,我们最终确定组合A2+B2+C2是最经济的组合。即磨细灰掺量占掺合料总量30%,外加剂掺量为1.6%,机制砂占总砂的30%。后续的配合比验证试验也证实了这一结论。
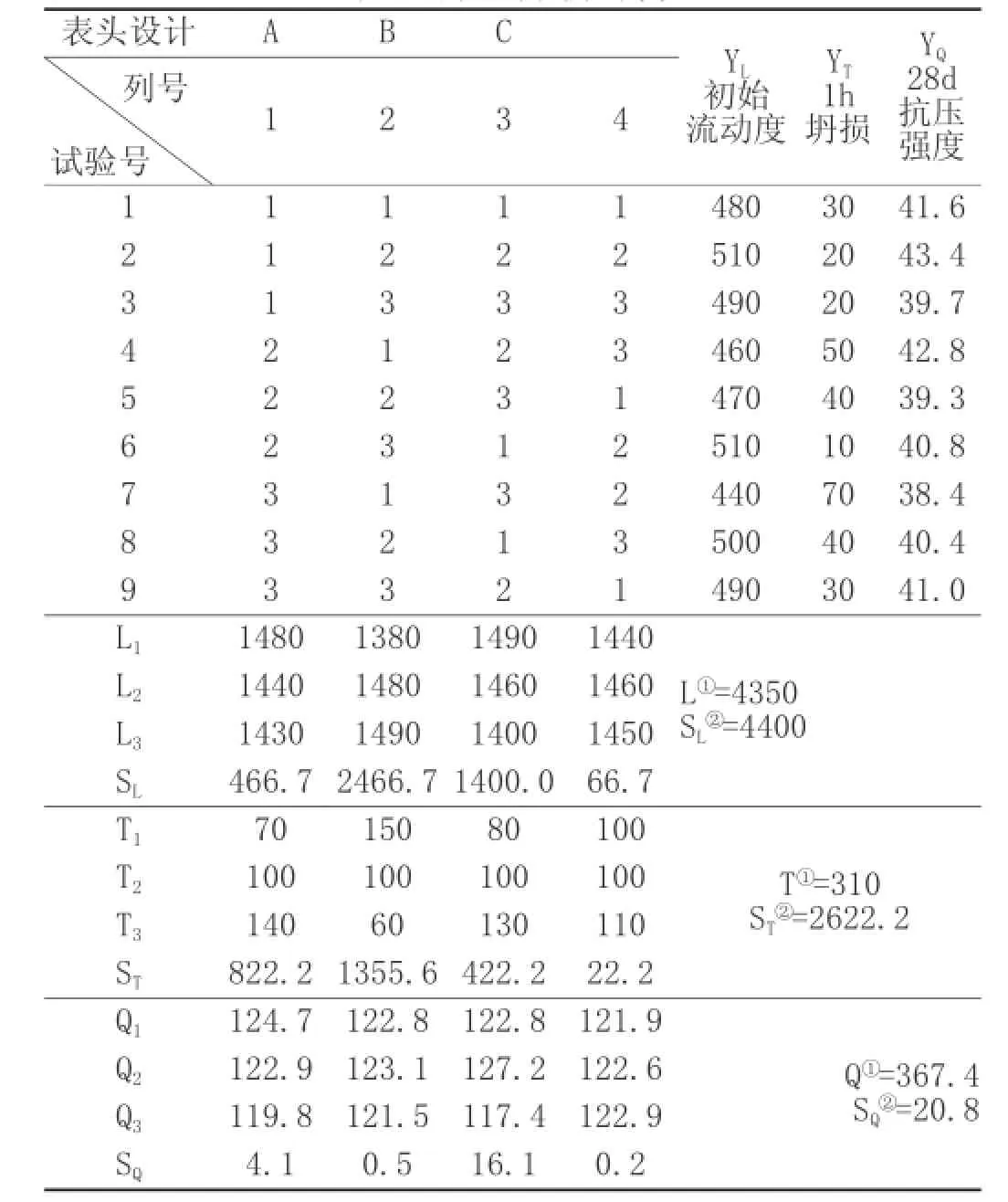
表5 方差分析计算
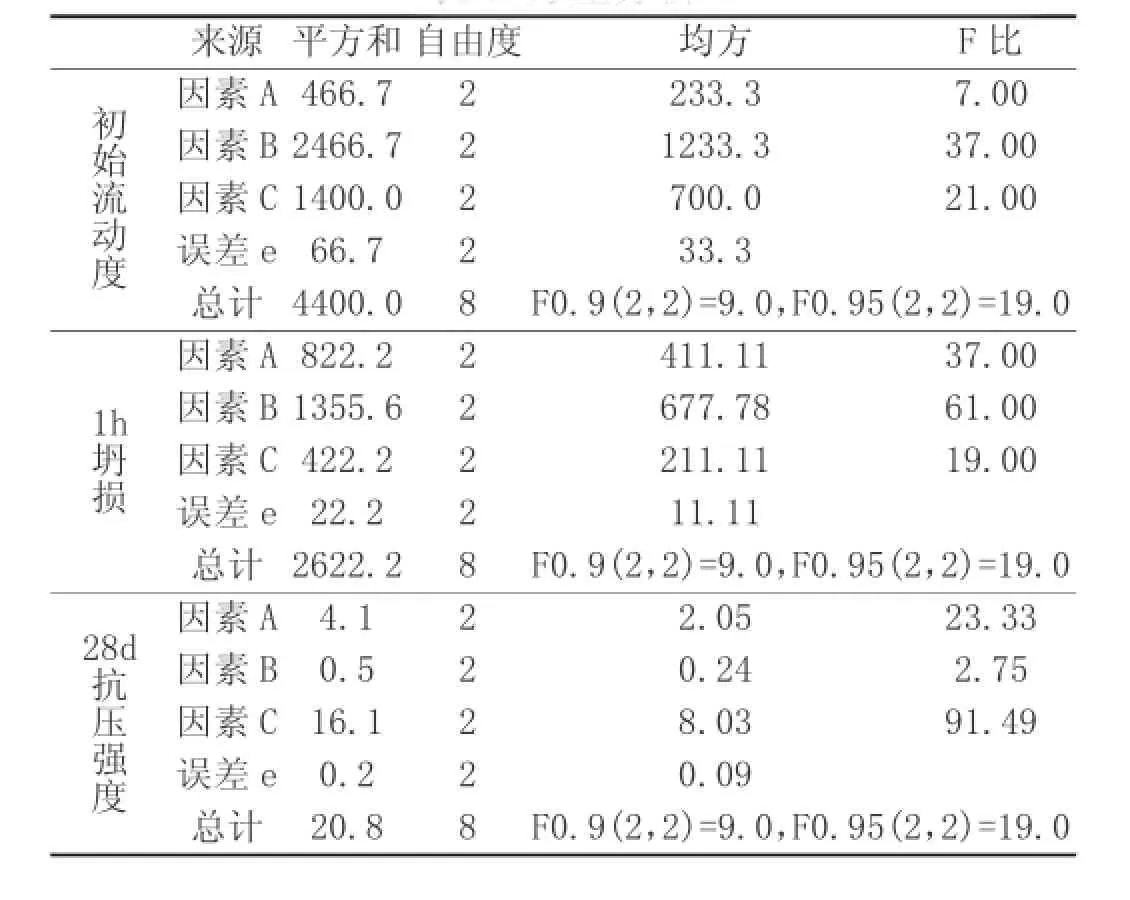
表6 方差分析
5 结束语
由于混凝土的性能指标较多,运用正交设计试验可能会出现针对不同的指标得出不同的最优组合的问题。因此需要我们综合考虑各项指标,在保证质量的前提下,兼顾生产成本等方面,最终合理地确定各因素的最佳水平。●
[1]成全喜,郑淑平,孙玉红.正交试验法在混凝土配合比设计中的应用[J].实验科学与技术.2006(06):28-30.
