基于空间索引的物流中心选址方法
2016-10-24陈丽,黄晋
陈 丽, 黄 晋
(1.广东交通职业技术学院计算机工程学院,广州 510650;2.华南师范大学计算机学院,广州 510631)
基于空间索引的物流中心选址方法
陈丽1, 黄晋2*
(1.广东交通职业技术学院计算机工程学院,广州 510650;2.华南师范大学计算机学院,广州 510631)
确定合理的城市物流节点位置,对优化物流网络、提高物流服务水平、改善城市交通状况都具有十分重要的作用. 文中提出了一种实用新型的选址查询方法,在已知人口分布和已建物流中心位置的基础上,从候选位置集中返回前k个最具有影响的位置,作为待建物流中心的参考,这种查询在决策支持系统中有广泛的应用. 该算法利用R-tree为3个已知位置集进行了索引,并提出基于候选位置影响力的排序方法,以此制定了有效的剪枝规则,大大减少了搜索复杂度. 实验表明,该算法具有很好的查询效率.
物流; 选址问题; 空间索引
Keywords:logistics;locationproblem;spatialindex
物流节点规划最早是从研究物流节点选址开始的,由于运输距离是物流成本最主要的开销,所以研究者一般关注如何使运输总距离或中心与顾客之间的最大距离最小化.
最小距离位置问题的目标是使得顾客和他们各自最近的设施之间的平均距离最小. 如:在给定的区域中找到一些最优的位置,使得顾客和他们各自的最近设施之间的平均距离最小[1];研究k-中心和k-中值查询,目标是从集合C中找到k个位置的集合C′,使得C′中的位置和C中的位置之间的平均距离最小[2];提出了路网中的最佳位置查询[3],并提出了一种动态监控方法[4],通过向表示路网的无向连通图插入所有的设施点和客户位置来构成新的无向连通图,根据设施点集合和客户位置集合发生的更新随时动态地查询最小化最大距离位置; 基于客户的最近位置分量技术提出了若干空间裁剪的策略,大大提高了最佳位置查询算法的性能,并进一步扩展了查询形式,提出了最佳多位置查询算法以及在3D路网空间中的查询算法[5-6]; 提出1个新的最小记录位置选择查询,在已知顾客集和现有设施集的情况下,可以从1个候选集中找到最佳的位置使得1个顾客和他的最近设施之间的平均距离最小[7]. 以上研究都是基于距离寻找最优解,因为他们关注的是所有设施的整体优化方案.
与本文研究比较接近的研究是最大影响设施位置问题,目标是使得位置的影响最大化,其中一个位置c的影响定义为c吸引的顾客的数量. 目前大多数研究是在欧几里德空间或lp标准空间处理问题,位置影响最大化问题也是在空间网络中研究.GHAEMI等[8]处理的问题中的查询对象和位置都在空间网络中.SHANG等[9]提出用弹道路径代表设施位置. 他们首先计算设施位置的逆最近弹道路径数量,再根据这个数量选择最有可能访问的位置. 针对数据集中包含不确定的实例,ZHENG等[10]提出把期望排名最高的位置作为最具有影响的位置,为高效地解决这个问题,提出了几个剪枝规则和一个分而治之的方法缩减位置的搜索空间和可能空间的数量.
本文所研究的是在规划区域内如何选定一个或者多个设施的地理位置,使得目标位置可以吸引尽可能多的顾客数(一般情况下顾客会选择离自己最近的物流中心):提出了一种新的Top-k位置查询方法,为选址问题提供了新的思路;提出了基于空间索引的搜索方法,对位置空间进行逐步剪枝,可避免重复计算节点;分别用真实和仿真数据集验证了算法的性能,证明了所提算法的有效性。
1 相关定义
首先给出逆最近邻和位置影响的正式定义. 给定C、F、M分别表示候选位置集合、已有物流中心集合和顾客位置集合. 图1中,f1和f2表示2个已有的物流中心位置,c1和c2表示2个候选的物流中心位置. 假设顾客总是优先选择最近的物流中心,那么每个位置吸引的顾客数可通过计算与它相连的实线数得到. 从图1可以看出,已有物流中心的顾客数有可能会因为新建的物流中心而减少(虚线),这种情况符合竞争的现实:当物流中心的负载超出了既定容量或出现了严重不平衡的情况,可以通过新建中心来改善这种情况.
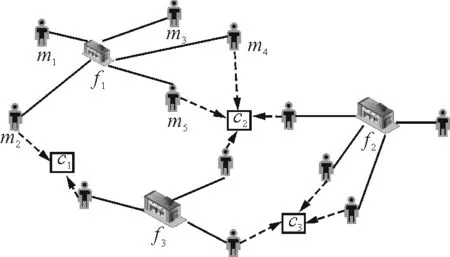
图1 基于位置影响的选址问题例子
本文探讨的物流中心选址问题是在已知人口分布M和已建物流中心F的情况下,在给定的候选位置集合C中,按影响大小给出Top-k个候选位置,作为待建物流中心的参考位置,这里,一个位置影响定义为把该位置视为是最近物流中心的顾客数量.
定义11个物流中心的逆最近邻是把其视为最近物流中心的所有顾客. 用d(f,m)表示f和m之间的欧几里德距离,min(m,F)表示m和F中的任一f之间距离的最小距离, f.RNN表示F中f的逆最近邻,即: f.RNN={mM|d(m,f )=min(m,F)}.
在图1中,物流中心f1的逆最近邻为 f1.RNN={m1,m2,m3,m4,m5}.

在图1中,If1=5,If2=4,If3=3.
当为1个新的物流中心选择位置时,我们的目标是找到1个在所有已有位置中最具有影响潜力的位置,也就是,新的物流中心影响的顾客越多,所在的候选位置就越好. 因此,给出如下定义.
定义3F表示已有物流中心集合,C表示候选位置的集合,任一候选位置c的影响潜力定义为I′c,是指当把它加入F后获得的影响,即I′c=Ic(F∪{c},M).
定义4给定候选位置集合C,Top-k个最具有影响的位置是C中影响潜力最大的k个位置.
在图1中,如果在位置c1新建物流中心,它会影响 f1和 f3的2个顾客(带有箭头的顾客指向c1);如果在位置c2新建物流中心,它会影响现有设施 f1、 f2和 f3中的4个顾客;如果在位置c3新建物流中心,它会影响 f2和 f3中的3个顾客. 因此,c1、c2和c3的影响潜力分别是2、4和3. 根据定义4,C中前2个最具有影响潜力的候选位置是c2和c3.
2 算法设计
2.1数据结构
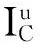
2.2影响关系的计算
对于候选位置集合C上的R-tree索引tC中的每一个节点nC,计算其影响值,即这个节点所对应的最小边界矩形(MinimumBoundingRectangle,MBR)中包含的候选位置影响的顾客数量,记为nC.SM. 同样,将tF中每一个节点nF的影响值记为nF.SM. 对于顾客集合M上的索引tM,每一个节点nM都对应2个集合nM.SC和nM.SF:集合nM.SC包含影响这个节点的MBR中所有用户的候选位置,集合nM.SF包含影响这个节点的MBR中所有用户的已有物流中心.
为有效计算给定节点的影响关系,介绍3种距离:给定2个节点,r1和r2分别表示它们的最小边界矩形,MinDist(r1,r2)和MaxDist(r1,r2)分别表示r1和r2之间的最小距离和最大距离;MinExisDistr2(r1)定义为r1中的点到r2中的点的最近邻的上界距离. 影响关系集nC.SM、nF.SM、nM.SC和nM.SF由如下定理决定.
定理1给定nCQC,若存在nF{nF|nMnC.SM,nFnM.SF},使得MinDist(rM,rC)≥MinExisDistrF(rM)成立,则rM中的顾客m不会被rC包含的任何候选位置c影响,其中rM和rC分别是节点nM和nC的MBR.
证明反证法. 假设rM包含的某位顾客m会被rC包含的某个候选位置c影响,根据定义2,d(c,m) 定理2给定nCQC,若对于任意的nF{nF|nMnC.SM,nFnM.SF},使得 MaxDist(rM,rC) 成立,则rM包含的顾客m会被rC包含的候选位置c影响. 证明因为MaxDist(rM,rC) 定理1说明如果节点nC距离节点nM比较远,其他nF节点距离节点nM更近,因为nF的存在,nM包含的顾客m不会被nC包含的候选位置c影响. 定理2说明如果没有其他nF节点比节点nC距离节点nM更近,那么nM包含的顾客m将会被nC包含的一些候选位置c影响. 定理1和定理2有助于理解节点对之间的影响关系. 为了进一步有效确定队列中节点的影响关系,我们计算QM中nM节点的距离阈值,分别用nM.dlow和nM.dupp存储rM和距离它最近的rF之间的下界距离和上界距离,即: nM.dlow=min({MinDist(rM,rF)|∀nFnM.SF}), nM.dupp=min({MinExistDist(rM)|∀nFnM.SF}). 根据定理1、定理2和存储的距离,给出3个有用的规则,从而确定节点nM及其子节点nM′的影响关系,并实现有效剪枝: 规则1:给定nC,如果存在nMnC.SM,使得nM.dlow>MaxDist(rC,rM)成立,根据定理2,对rM包含的任意m和rc包含的任意c,m会被c影响. 因为,我们确定rM中的顾客会被影响,节点nM应该从nC.SM中移除,节点nC应该从nM.SC中移除. 同时,对于rc包含的应该以递增. 规则2:给定nC,如果存在nMnC.SM,使得 MinDist(rM,rC)≥nM.dupp 成立,根据定理1,对rM包含的任意m和rc包含的任意c,m不会被rC影响. 因此,节点nM和节点nC应该分别从nC.SM和nM.SC中移除. 规则3:与规则2相似,给定nF,如果存在nMnF.SM,使得MinDist(rM,rF)≥nM.dupp成立,对rM包含的任意m和rf包含的任意f,m不会被f影响. 因此,节点nM和节点nF应该分别从nF.SM和nM.SF中移除. 2.3影响力的计算 2.4算法伪代码 根据上述规则以及对影响力的观察,我们设计了以下基于空间索引的选址算法: 算法1基于空间索引的Top-k最具影响位置查询 输入:tC,tF,tM的树根rootC,rootF,rootM 输出:Top-k(M,F,C) 将树根rootC,rootF,rootM插入到优先队列QC,QF,QM中; 初始化3个优先队列的影响关系信息; while∀nCQC,第k大的 ProEntry(QM); ProEntry(QF); ProEntry(QC); returnTop-k(M,F,C) ProEntry(Q) 从队列Q中选取具有最大n.inf值的节点n; ifn是一个中间节点then 扩展n; foreachn的子节点n′do 计算n′的影响关系; 更新与n′相关的其他节点的影响关系; 使用规则1~规则3剪枝节点; 将n′插入到Q; ifn是一个叶子节点then ifnQCthen ifIu>目前第k大的Icthen foreachcndo计算Ic. 2.5时间复杂度分析 算法1首先为候选位置集合C、已有物流中心集合F和顾客位置集合M建立R-tree树索引,这一步的时间复杂度是:O(|C|log|C|)、O(|F|log|F|)和O(|M|log|M|). 在实际应用中,这3个索引的建立和维护可以线下完成. 由于建立了R-tree索引,算法1的主要时间消耗为计算入口节点的影响力、影响关系等信息以及其他关联节点的影响关系的更新. 初始化3个优先队列的影响关系只需遍历一次入口节点的父节点的影响关系集,则时间复杂度为O(e),其中e为3个索引入口节点的平均大小. 更新其他关联节点的影响关系的计算比较复杂:对于QM中的每个入口节点,需要检查nCnM.SC和nFnM.SF是否可以裁剪,如果nC更新了,还需检查nMnC.SM是否需要进一步更新,需要O(e2)的时间代价. 对于QC中的每个入口节点,需判断nMnC.SM是否需要裁剪,需要O(e)的代价. 对于QF中的每个入口节点,首先需要判断nMnF.SM是否已被裁剪,若未被裁剪,则需要更新它的上下界距离. 此外,还需再次检查nCnM.SC和nFnM.SF在更新距离后是否需要裁剪,如果更新了nC,需进一步计算nC.SM中的节点nM的影响上界值,这个过程的时间消耗是O(3e2). 为了方便计算,假设每一个集合大小都为O(n). 最好情况下,只需访问前k个影响力最大的节点,因此,共访问了O(klogn)次nC,while语句只需执行O(logn)次,该算法的总代价是O(nlogn)+O(logn)×(O(1)+O(12)+O(1)+O(13))=O(nlogn). 根据定义4,可通过简单方式实现所述查询:依次把候选集C中的每个候选位置c加入到已有物流中心集合F中,扫描顾客集合M找出c的逆最近邻,统计c的影响潜力,返回前k个即可. 我们将这种实现方法称为顺序扫描法(简称为SS算法),作为实验中的对比算法. 实验中本文算法简称为PA算法. 所有算法都在3.44GHz、6核CPU和8GB内存的工作站上运行,操作系统为Windows7 64-bit. 所有的算法用C++实现. 实验使用了模拟数据和真实数据. 生成的模拟数据集包含20个集群,分别符合高斯分布和齐普夫分布. 真实数据集包括1 560 253个美国加州洛杉矶的地理位置,由OpenStreetMap[12]提供. 我们在数据集中随机抽取一定数量的位置点构成集合C、F和M. 3.13个位置集合大小对查询性能的影响 我们首先在不同的数据分布下考察了候选位置、已有物流中心和顾客等3个位置集合的大小对查询性能的影响. 从图2~图4可以看出,随着集合的增大,查询算法的响应时间逐步上升. 总的来说,PA算法在响应时间上比顺序扫描算法要高出1个数量级. 原因是PA算法对节点的影响力进行了排序,并按这个优先序进行遍历;3个剪枝规则大大降低了搜索空间的复杂度,避免了不必要的计算. 因此,PA算法在运行时间上的性能最好. 图2 候选位置数|C|在不同的数据分布上对查询时间的影响 图3 已有物流中心数|F|在不同的数据分布上对查询时间的影响 图4 顾客数|M|在不同的数据分布上对查询时间的影响 3.2参数k对查询性能的影响 图5 参数k在齐普夫数据上对查询时间的影响 Figure5EffectonquerytimeoftheparameterkunderZipf’sdistribution 对于城市的经济环境和生态环境而言,物流节点都具有重要的战略意义,选址合理的物流中心不仅有助于加快货物流动速度、减少不必要的配送成本,还能解决城市功能紊乱、缓解交通拥挤、减轻环境压力. 本文提出了一种新型且实用的位置选择查询,并基于空间索引和剪枝策略实现了这种查询,仿真数据集和真实数据集上的详尽实验都证明了所提算法的有效性. 而在数据倾斜的情况下如何进一步提高算法的可适应以及在大数据规模下实现其分布式是我们日后将努力解决的问题. [1]ZHANGD,DUY,XIAT,etal.Progressivecomputationofthemin-distoptimallocationquery[C]∥Proceedingsofthe32ndInternationalConferenceonVeryLargeDataBases.Seoul,Korea:ACM, 2006:643-654. [2]MOURATIDISK,PAPADIASD,PAPADIMITRIOUS.Medoidqueriesinlargespatialdatabases[C]∥MEDEIROSCB,EGENHOFERMJ,BERTINOE.Proceedingsofthe9thInternationalSymposiumonSpatialandTemporalDatabases.Berlin:Springer, 2005:55-72. [3]XIAOXK,YAOB,LIFF.Optimallocationqueriesinroadnetworkdatabases[C]∥Proceedingsof27thIEEEInternationalConferenceonDataEngineering.Hannover:[s.n.] ,2011:804-815. [4]YAOB,XIAOXK,LIFF,etal.Dynamicmonitoringofoptimallocationsinroadnetworkdatabases[J].InternationalJournalonVeryLargeDataBases, 2014, 23(5):697-720. [5]LIUYB,WONGCW,WANGK,etal.Anewapproachformaximizingbichromaticreversenearestneighborsearch[J].KnowledgeandInformationSystems,2013, 36(1):23-58. [6]CHENZT,LIUYB,WONGCW,etal.Efficientalgorithmsforoptimallocationqueriesinroadnetworks[C]∥Proceedingsofthe2014ACMSIGMODInternationalConferenceonManagementofData.NewYork:ACM, 2014:123-134. [7]QIJZ,ZHANGR,WANGYQ,etal.Themin-distlocationselectionandfacilityreplacementqueries[J].WorldWideWeb, 2014, 17(6):1261-1293. [8]GHAEMIP,SHAHABIK,WILSONJP,etal.Optimalnetworklocationqueries[C]∥Proceedingsofthe18thInternationalConferenceonAdvancesinGeographicInformationSystems.NewYork:ACM, 2010:478-481. [9]SHANGS,YUANB,DENGK,etal.Findingthemostaccessiblelocations-reversepathnearestneighborqueryinroadnetworkscategoriesandsubjectdescriptors[C]∥Proceedingsofthe19thACMInternationalConferenceonAdvancesinGeographicInformationSystems.NewYork:ACM,2011:181-190. [10]ZHENGK,HUANGZ,ZHOUA,etal.Discoveringthemostinfluentialsitesoveruncertaindata:arankbasedapproach[J].IEEETransactionsonKnowledge&DataEngineering,2012, 24(12):2156-2169. [11]GUTTMANA.R-trees:adynamicindexstructureforspatialsearching[C]∥Proceedingsofthe1984ACMSIGMODInternationalConferenceonManagementofData.NewYork:ACM, 1984:47-57. [12]OpenStreetMap[Z/OL]. [2015-09-25].http:∥www.openstreetmap.org/. 【中文责编:庄晓琼英文责编:肖菁】 A Selection Method Based on Spatial Index for Logistics Center Location CHENLi1,HUANGJin2* (1.SchoolofComputerEngineering,GuangdongCommunicationPolytechnic,Guangzhou510650,China;>2.SchoolofComputerScience,SouthChinaNormalUniversity,Guangzhou510631,China) Todeterminereasonablelocationsforlogisticsnodeswillbehelpfulforoptimizinglogisticsnetwork,improvinglogisticsservicesandalleviatingurbantrafficconditions.Anovelandpracticallocationqueryisproposed,thatis,givenpopulationdistributionandexistinglogisticsnodes,itistoretrievetheTop-kmostinfluentiallocationsfromacandidateset,whichcanbetakenascandidatelocationsfornewlogisticsnodes.Thisnewquerytypewillbewidelyusedindecisionsupportsystem.R-treeindexesarebuiltforthethreelocationsetsandrankingmethodarepresentedforcandidatelocations’importance.Furthermore,threeeffectivepruningrulesareaddressedtoreducethesearchcomplexitydramatically.Experimentsdemonstratethatthepresentedalgorithmhasgoodqueryefficiencyandthepruningstrategiesareveryeffective. 2015-10-21《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(61272065);广东省自然科学基金项目(S2012010009311) 黄晋,副研究员,Email:jinhuang@scnu.edu.cn. TP315 A 1000-5463(2016)04-0113-06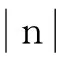






3 实验与分析



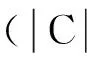

4 小结
