人工自旋轨道耦合玻色-爱因斯坦凝聚体的元激发
2016-10-24张丹伟
张丹伟, 曹 帅
(1.华南师范大学物理与电信工程学院,广州 510006;2.华南农业大学电子工程学院应用物理系,广州 510642)
人工自旋轨道耦合玻色-爱因斯坦凝聚体的元激发
张丹伟1*, 曹帅2*
(1.华南师范大学物理与电信工程学院,广州 510006;2.华南农业大学电子工程学院应用物理系,广州 510642)
文章研究了准一维人工自旋轨道耦合玻色-爱因斯坦凝聚体中的元激发. 利用平均场理论和波戈留波夫近似方法,分别计算了此原子凝聚体在依赖于拉曼耦合强度的零动量相和平面波相的激发谱. 结果表明,在零动量相时体系激发谱的2个分支都呈现出对称结构;相反地,在较小拉曼耦合强度时的平面波相,激发谱呈现出旋子最低结构,从而预示了体系从平面波相到条纹相的相变. 文中证明了在平面波相和零动量相的相变附近,低频元激发的声速急剧下降并消失于相变点. 文章全面分析了人工自旋轨道耦合原子凝聚体的元激发特性,为实验研究该类崭新的多体系统提供理论支持.
元激发; 激发谱; 玻色-爱因斯坦凝聚体; 人工自旋轨道耦合; 波戈留波夫近似
Spin-orbit (SO) coupling plays an important role in many exotic effects or phenomena in condensed matter physics, such as the spin Hall effects and topological states[1-4]. Recently, the experimental realization of SO coupling for ultra-cold atomic gases by using Raman lasers[5]provides a unique platform to study novel properties of SO-coupled bosons and typically Bose-Einstein condensates (BECs)[6-10]. These systems have no direct analog in solids and thus have attracted great attention for different types of SO coupling and different external conditions[11-12]. In particular, the static properties of SO-coupled BECs have been studied extensively, and the rich phase diagrams of the many-body ground states are explored[13-15]. Remarkably, depending on the interatomic interactions and the Raman coupling strength, the ground state of a spinor BEC with equal Rashba-Dresselhaus SO coupling can exhibit three different quantum phases[14-15], which are the conventional zero-momentum phase, the plane-wave phase with condensate in a single non-zero momentum state, and a stripe phase with condensate in two opposite momenta, respectively. Other exotic ground states are also revealed when the SO-coupled BECs are subjected to external potentials or optical lattices, such as the vortex and Skyrmion crystal states[16].
The quantum dynamics and collective excitations are also important in exploring the properties of ultracold atomic gases. For the SO-coupled BECs, their dynamics has also been studied in different contexts. For example, the SO-coupled BECs have been demonstrated to exhibit unconventional collective dipole oscillations[7], spin Josephson effects[17], nonlinear soliton dynamics[18-19], and interesting relativistic dynamics, such as analogs of self-localization[20], Zitterbewegung[8-9], and Klein tunneling[21]under certain conditions. In addition, the collective and excited modes of the SO-coupled BECs have attracted increasing interest, and some of them have been studied by using the hydrodynamic or sum-rule approach[22-26].
In this paper, we investigate the elementary excitations in a quasi-one-dimensional BEC with Raman-induced SO coupling. Based on the mean-field approximation and the Bogoliubov approach, we calculate the excitation spectrum of the SO-coupled BEC in the zero-momentum and plane-wave phases, respectively. The two branches of the excitation spectrum in the zero-momentum phase both exhibit symmetry structures. In contrast, the excitation spectrum exhibits roton minimum structure in the plane-wave phase for small Raman coupling strength, and the roton mode provides the onset of the phase transition to the stripe phase. We also calculate the sound speed of the low-frequency excitations as functions of the Raman coupling strength, which decreases sharply and becomes zero near the phase transition between the plane-wave and zero-momentum phases, indicating the softening of the phonon mode.
1 Model system
Let us begin with a spinor BEC trapped in one dimension with two atomic hyperfine spin states acting as an effective spin-1/2 system. We consider the BEC with the equal contributions of Rashba and Dresselhaus SO coupling, which has been generated in experiments by dressing the atoms with two counterpropagating Raman lasers (i.e., the Raman transition)[6-10]. The single particle Hamiltonian of this SO-coupled BEC can be written as (we setħ=m=1 withmdenoting the atomic mass)

(1)
The single particle energy spectrum is obtained as
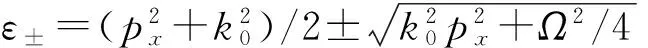
(2)
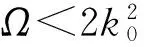
Within the mean-field approximation, the interaction Hamiltonian of the atomic gas can be written as
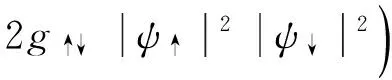
(3)
2 Elementary excitations and the excitation spectrum

(4)

(5)
We consider the SO-coupled BEC initially prepared in the zero-momentum or plane-wave phase, and then the ground-state wave function in the two cases can be written as[14-15]
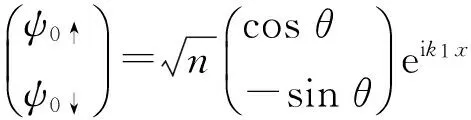
(6)
To evaluate the elementary excitations, we apply the Bogoliubov approach by considering the deviations of the wave functions with respect to ground states as

(7)
wherej={↑,↓},δψj(t) denotes the perturbations, andμis the chemical potential of the ground state. The perturbations can be written as the following form:
δψj(t)=ujei(qx+k1)xe-iωt+v*je-i(qx-k1)xeiωt,
(8)
where(uj,vj) and its conjugate (u*j,v*j)denotes the complex amplitudes of the excitations, andωandqxare the excitation frequency and wave vector along thexdirection, respectively. Inserting the total wave function (7) into the Gross-Pitaevskii equations yields the linearized equations for the perturbations:
gncos2θ(2δψ↑+δψ*↑e2ik1x)+
g12nsinθcosθ(tanθδψ↑-δψ↓-δψ*↓e2ik1x),
(9)
gnsin2θ(2δψ↓+δψ*↓e2ik1x)+
g12nsinθcosθ(cotθδψ↓-δψ↑-δψ*↑e2ik1x),
(10)
Substituting the expansion (8) into the above equations, we obtain the eigen-equation for the excitation modes:

(11)

M24=-M42=gnsin2θ, andM34=-M43=-M12.

For the zero-momentum phase, we obtain two separated branches of the excitation spectrum with typical examples shown in Figure 1. In the upper and lower branches, the excitation spectra are both symmetric under the inversion ofqxinto -qx. Near the vicinity ofqx=0 in the lower branch approaching the dispersion of the phonon mode, the spectrum is parabola-like for rela-tively smaller Raman coupling strength, while becomes linearized with the increase of the strength as shown in Figure 1B, indicating the non-monotonic dependence of the phonon velocity as we will discuss below.

Figure 1 The excitation spectrum in the zero-momentum phase as a function of qx
For the plane-wave phase, the two branches of the excitation spectrum exhibitqx-inversion-symmetry breaking due to the finite condensate momentumk1≠0. In this case, the typical examples are shown in Figure 2. For the lower branch that we are interested in, the excitation spectrum has another local minimum for negative values ofqx, which is attributed as a roton minimum. As shown in Figure 2B, the emergence of the roton minimum becomes more and more pronounced as the SO-coupled BEC approaches the phase transition to the stripe phase (whenΩ<Ω1) by decreasing the Raman coupling strength , and thus provides the onset of this phase transition. As increasingΩ, the BEC approaches the zero-momentum phase, and the roton minimum disappears before the phase transition point (Ω=Ω2), which shows the softening of the roton mode. The phy-sical origin of the roton minimum is due to the degeneracy of the ground state. For the single-particle dispersion, the lower branch has two degenerate minimum for relative small atpx=±k1, and has a single minima atpx=0 for relative largerΩ. With the interatomic interactions being taken into account, the atoms condenses atk1or -k1in the plane-wave phase, which are two degenerate states. In this case, when the BEC is subjected to perturbations, it is very favorable for atoms to be transferred to the empty state, resulting in the emergence of a roton minimum. In experiments, the excitation spectrum of the BECs can be measured by using the Bragg spectroscopy[10].

Figure 2The excitation spectrum in the planewave phase as a function ofqx, and the sound velocity of the low-frequency excitations as a function of the Raman coupling strength
Finally in this section, we study the sound velocity of the low-frequency excitations in the SO-coupled BEC. In the long wavelength limitqx→0, the lower excitation spectrum exhibits linear dispersion for the phonon mode, and thus the dispersion can be written asω-=vqx, wherevis the sound velocity along thexdirection. In Figure 2C, we numerically calculate and show the sound velocity of the phonon mode as a function of the Raman coupling strengthv(Ω)for the typical parameters. The result shows the sound velocity decreases sharply and vanishes near the phase transition between the plane-wave and zero-momentum phases atΩ=Ω2. This non-monotonic behavior of the sound velocity can be interpreted by the effective mass associated with the single-particle spectrum. At the transition between the plane-wave and zero-momentum phases, the effective mass of the phonon mode becomes divergent, resulting in the strong reduction of the sound velocity.
3 Conclusion
In summary, we investigate the elementary excitations in a quasi-one-dimensional BEC with Raman-induced SO coupling. Based on the mean-field approximation and the Bogoliubov approach, we calculate the excitation spectrum of the atomic condensate in the zero-momentum and plane-wave phases. We show that the two branches of the excitation spectrum in the zero-momentum phase both exhibit symmetry structures. In contrast, the excitation spectrum exhibits the roton minimum structure with the roton mode in the plane-wave phase, which provides the onset of the phase transition to the stripe phase. We also point out that the sound speed of the phonon mode decreases sharply and vanishes at the phase transition between the plane-wave and zero-momentum phases. This work presents comprehensive analysis of novel properties of elementary excitations in a synthetic spin-orbit-coupled atomic condensate, which may provide theoretical support for experimental studies on this new kind of many-body system.
[1]SINOVA J, VALENZUELA S O, WUNDERLICH J, et al. Spin Hall effects[J]. Reviews of Modern Physics, 2015, 87(4): 1213-1259.
[2]HASAN M Z, KANE C L. Colloquium: topological insulators[J]. Reviews of Modern Physics, 2010, 82(4): 3045-3067.
[3]QI X L, ZHANG S C.Topological insulators and superconductors[J]. Reviews of Modern Physics, 2011, 83(4): 1057-1110.
[4]ZHANG D W, WANG Z D, ZHU S L. Relativistic quantum effects of Dirac particles simulated by ultracold atoms[J]. Frontiers of Physics, 2012, 7(1): 31-53.
[5]杜炎雄,程爱琴,郑翔,等. 量子网络研究进展[J].华南师范大学学报(自然科学版),2016,48(1): 16-22.
DU Y X, CHENG A Q, ZHENG X, et al. Research progress on Quantum network[J]. Journal of South China Normal University (Natural Science Edition), 2016,48(1): 16-22.
[7]ZHANG J Y, JI S C, CHEN Z, et al. Collective dipole oscillations of a spin-orbit coupled Bose-Einstein condensate[J]. Physical Review Letters, 2012, 109: Art 115301, 5pp.
[8]QU C, HAMNER C, GONG M, et al. Observation of Zitterbewegung in a spin-orbit-coupled Bose-Einstein condensate[J]. Physical Review A, 2013, 88: Art 021604, 5pp.
[9]LEBLANC L J, BEELER M C, JIMENEZ-GARCIA K, et al. Direct observation of zitterbewegung in a Bose-Einstein condensate[J]. New Journal of Physics, 2013, 15: Art 073011, 11pp.
[10]JI S C, ZHANG L, XU X T, et al. Softening of roton and phonon modes in a Bose-Einstein condensate with spin-orbit coupling[J]. Physical Review Letters, 2015, 114: Art 105301, 5pp.
[11]DALIBARD J, GERBIER F, JUZELIUNAS G,et al. Colloquium: artificial gauge potentials for neutral atoms[J]. Reviews of Modern Physics, 2011, 83(4): 1523-1543.
[12]GALITSKI V, SPIELMAN I B.Spin-orbit coupling in quantum gases[J]. Nature, 2013, 494: 49-54.
[13]WANG C, GAO C, JIAN C M,et al. Spin-orbit coupled spinor Bose-Einstein condensates[J]. Physical Review Letters, 2010, 105: Art 160403, 4pp.
[14]HO T L, ZHANG S.Bose-Einstein condensates with spin-orbit interaction[J]. Physical Review Letters, 2011, 107: Art 150403, 5pp.
[15]LI Y, PITAEVSKII L P, STRINGARI S.Quantum tricriticality and phase transitions in spin-orbit coupled Bose-Einstein condensates[J]. Physical Review Letters, 2012, 108: Art 225301, 5pp.
[16]ZHANG D W, CHEN J P, SHAN C J, et al. Superfluid and magnetic states of an ultracold Bose gas with synthetic three-dimensional spin-orbit coupling in an optical lattice[J]. Physical Review A, 2013, 88: Art 013612, 8pp.
[17]ZHANG D W, FU L B, WANG Z D, et al. Josephson dynamics of a spin-orbit-coupled Bose-Einstein condensate in a double-well potential[J]. Physical Review A, 2012, 85: Art 043609, 9pp.
[18]XU Y, ZHANG Y, WU B.Bright solitons in spin-orbit-coupled Bose-Einstein condensates[J]. Physical Review A, 2013, 87: Art 013614, 5pp.
[19]CAO S, SHAN C J, ZHANG D W, et al. Dynamical generation of dark solitons in spin-orbit-coupled Bose-Einstein condensates[J]. Journal of the Optical Society of America B, 2015, 32(2): 201-209.
[20]MERKL M, JACOB A, ZIMMER F E, et al. Chiral confinement in quasirelativistic Bose-Einstein condensates[J]. Physical Review Letters, 2010, 104: Art 073603, 4pp.
[21]ZHANG D W, XUE Z Y, YAN H, et al. Macroscopic Klein tunneling in spin-orbit-coupled Bose-Einstein condensates[J]. Physical Review A, 2012, 85: Art 013628, 6pp.
[22]ZHENG W, LI Z.Collective modes of a spin-orbit-coupled Bose-Einstein condensate: a hydrodynamic approach[J]. Physical Review A, 2012, 85: Art 053607, 11pp.
[23]LI Y, PITAEVSKII L P, STRINGARI S. Sum rules, dipole oscillation and spin polarizability of a spin-orbit coupled quantum gas[J]. Europhysics Letters, 2012, 99(4): Art 56008, 5pp.
[24]MARTONE G I, LI Y, PITAEVSKII L P, et al. Anisotropic dynamics of a spin-orbit-coupled Bose-Einstein condensate[J]. Physical Review A, 2012, 86: Art 063621, 8pp.
[25]LI Y, MARTONE G I, PITAEVSKII L P, et al. Superstripes and the excitation spectrum of a spin-orbit-coupled Bose-Einstein condensate[J]. Physical Review Letters, 2013, 110: Art 235302, 5pp.
[26]YU Z Q. Phase transitions and elementary excitations in spin-1 Bose gases with Raman-induced spin-orbit coupling[J]. Physical Review A, 2016, 93: Art 033648, 11pp.
【中文责编:成文英文责编:李海航】
