广义非线性扩散方程的条件 Lie-Bäcklund对称和不变子空间

夏亚荣

(1.西北大学 数学学院, 陕西 西安　710127; 2.西安文理学院 信息工程学院, 陕西 西安　710065)



广义非线性扩散方程的条件 Lie-Bäcklund对称和不变子空间

夏亚荣1,2

(1.西北大学 数学学院, 陕西 西安710127; 2.西安文理学院 信息工程学院, 陕西 西安710065)

运用不变子空间方法和条件 Lie-Bäcklund 对称研究广义非线性扩散方程，得到了方程允许的不变子空间, 等价于方程的高阶条件Lie-Bäcklund对称。最后通过例子构造出一些广义非线性反应扩散方程的广义泛函分离变量解。

非线性扩散方程; 不变子空间; 条件 Lie-Bäcklund 对称; 广义泛函分离变量解

O175.14

ADOI：10.16152/j.cnki.xdxbzr.2016-01-003

非线性现象广泛地呈现在物理、生物、化学等领域。近年来, 对于描述非线性现象的非线性偏微分方程的求解已成为广大科学工作者的重要研究课题之一。对称群理论在构造非线性偏微分方程的精确解中发挥了重要的作用, 最早由Lie提出, 即Lie点对称方法；Bluman和Cole推广了Lie点对称方法, 提出了非经典对称方法(即条件对称方法)；Fokas和Liu推广了条件对称方法, 提出了条件 Lie-Bäcklund 对称方法[1]；Ji在文献[2]中首次提出利用变换v=f(u)将非线性条件 Lie-Bäcklund 对称线性化, 再利用与条件Lie-Bäcklund 对称方法相关的不变子空间方法[3]构造广义泛函分离变量解。

本文主要利用此方法研究了一类在物理中有重要意义的广义非线性反应扩散方程

ut=[D(u)ux]x+g(x)Q(u)。

(1)

其中D(u),Q(u)分别称为对流项和源项。

1　条件 Lie-Bäcklund 对称和不变子空间理论

令

(2)

是具有特征 η=P[u] 的演化向量场,且

ut=F(x,t,u,u1,u2,…，un)

(3)

为一非线性演化方程,其中

定义1演化向量场 (2) 是方程 (1) 的Lie-Bäcklund对称当且仅当

V(ut-F[u])|L=0。

(4)

定义2演化向量场(2)是方程(1)的条件Lie-Bäcklund对称当且仅当

V(ut-F[u])|L∩M=0。

(5)

命题1[1,4]方程 (1) 允许条件Lie-Bäcklund对称 (2) 的充分条件是存在一个函数 H(t,x,u,η), 使得

H(t,x,u,0)=0。

(6)

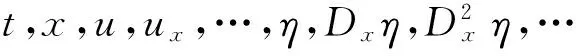
若 η 不显含 t, 由命题1知,方程(1)允许特征为η的条件Lie-Bäcklund对称当且仅当

Dtη=0。

(7)

设有限维线性空间

Wk=L{(f1(x),f2(x),…，fk(x)}=

(8)

在给定算子 F 下不变,当且仅当 F[Wk]⊆Wk, 线性空间 Wk称为非线性微分算子F的不变子空间,即

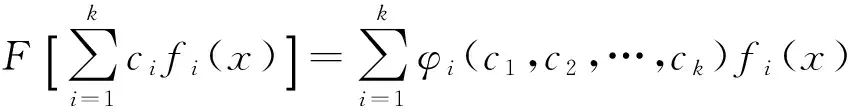
如果线性子空间 Wk在给定算子 F 作用下不变,那么方程(3)有广义变量分离解

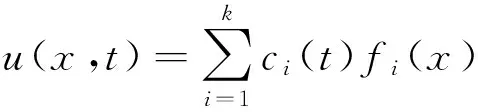
假设不变子空间 Wk是 n 阶线性常微分方程

L[y]=y(n)+an-1(x)y(n-1)+…

a1(x)y′+a0(x)y=0

(9)

的解空间,则微分算子F允许不变子空间 Wk的不变条件是

DnF+an-1(x)D(n-1)F+…+a1(x)DF+

a0(x)F|[H]=0。

(10)

η=[f(u)]lx+a1(x)[f(u)](l-1)x+…+

al(x)f(u)

(11)

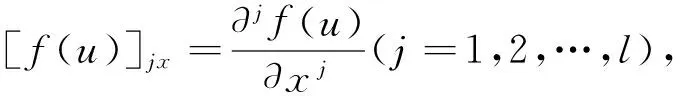
定理1[1,5]若线性空间 (8) 在具有阶数为j的算子作用下是不变的,则l≤2j+1。

2　主要结果

现在考虑方程(1)的条件Lie-Bäcklund对称 (11), 研究方程(1)的条件Lie-Bäcklund对称(11)等价于研究方程

(12)

的条件Lie-Bäcklund对称

σ=vlx+a1(x)v(l-1)x+…+al(x)v。

(13)

其中

且′表示对隐含变量的导数,u=f-1(v) 为v=f(u) 的反函数。

当l=2时,由命题1知方程(12) 允许条件Lie-Bäcklund对称的充分条件是

其中′表示对隐含变量的导数,取上述关于vx的多项式的系数为零,可得方程 (12) 及其相应的条件Lie-Bäcklund对称(13)中的未知函数满足下面的决定方程组:

B″=0,-a1(A″+4B′)=0,

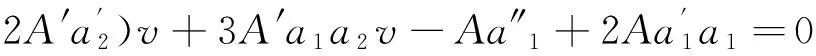
gF′a2v=0。

求解上面的常微分方程组,可以对允许二阶条件Lie-Bäcklund对称(13)的方程(12)进行分类。

表1和表2 中的未知函数如下:

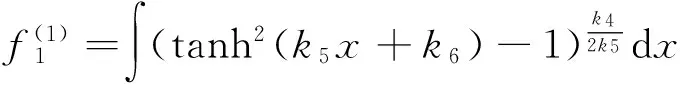
当l=2时，方程(12) 的条件Lie-Bäcklund对称 (13) 和不变子空间Wl。

表1当n=2时方程(12)的分类及其允许的Lie-Bäcklund对称与不变子空间

Tab.1Whenn=2 the classification of equation (12) the conditional Lie-Bäcklund symmerty and the invariant subspace which admits

序号方程条件Lie-Bäcklund对称不变子空间1vt=A(v)vxx+(b1v+b2)v2x+g1(f1v+f2)η=vxxW{1,x}2vt=-2b1v2vxx+(b1v+b2)v2xη=vxx+1-x+c3vxW{1,(x-c3)2}3vt=-2b1v2vxx+(b1v+b2)v2x+c8c5+c6v-b23b1()3+c7v-b23b1()[]η=vxx+k4tanh(k5x+k6)vxW{1,f(1)1(x)}4vt=-2b1v2vxx+(b1v+b2)v2x+c9(c10x2+c11x+c12)η=vxx+2c102c10x+c11vxW{1,x2}5vt=(-2b1v2+c1v)vxx+(b1v+b2)v2xη=vxx+1-x+c13W{1,(x-c13)2}6vt=(-2b1v2+c1v)vxx+(b1v+b2)v2x+c14[c15+c16v-c1+b23b1()3+c17v-c1+b23b1()η=vxx+k7tanh(k8x+k9)vxW{1,f(1)2(x)}7vt=(-2b1v2+c1v)vxx+(b1v+b2)v2x+c18(c19x2+c20x+c21)η=vxx+2c192c19x+c20vxW1,x+c202c19()2{}8vt=(-2b1v2+c2)vxx+(b1v+b2)v2xη=vxx+1-x+c21W{1,(x-c21)2}9vt=(-2b1v2+c2)vxx+(b1v+b2)v2x+c22(c23x2+c24x+c25)η=vxx+2c232c23x+c24vxW1,x+c242c23()2{}

类似的,可以分别对允许三阶、四阶及五阶的条件Lie-Bäcklund对称(13) 的方程 (12) 进行分类, 结果如下。 文中的bi,ci,ki,pi均表示任意常数。

3　方程 (10) 的泛函广义分离变量解

变化v=f(u)不仅将方程(12)允许的条件Lie-Bäcklund对称 (13) 变换为方程(1)所允许的条件Lie-Bäcklund对称 (11), 还将方程(12)定义在不变子空间(8)上的广义分离变量解

v(x,t)=c1(t)f1(x)+c2(t)f2(x)+…+

ck(t)fk(x)

(14)

变换为方程 (1) 的泛函广义分离变量解

f(u)=c1(t)f1(x)+c2(t)f2(x)+…+

ck(t)fk(x)。

(15)

这两个解中的未知函数 ci(t) 满足有限维的动力系统, 该系统是将式(14)代入(12)后取fi(x)左右两边的系数相等而得。下面通过例子解释这个过程。

表2当n≥3时方程(12)的分类及其允许的Lie-Bäcklund对称与不变子空间

Tab.2Whenn≥3 the classification of equation (12) the conditional Lie-Bäcklund symmerty and the invariant subspace which admits

序号方程条件Lie-Bäcklund对称不变子空间1vt=v2vxx+(p1v+p2)v2x+p3(k1v2+k2v+k3)η=vxxx+svxx-svxW{1,f(2)1(x),f(2)2(x)}2vt=(p1v3+p2v2+p3v+p4)vxx+p4v2v2x+p5(k1v2+k2v+k3)η=vxxx+svxx-svxW{1,f(2)1(x),f(2)2(x)}3vt=(p1v3+p2v2+p3v+p4)vxx+(p4v2+p1v+p2)v2x+p6(k1v2+k2v+k3)η=vxxx+svxx-svxW{1,f(2)1(x),f(2)2(x)}

例1方程

(16)

允许的二阶条件Lie-Bäcklund对称是

η=vxx。

(17)

方程 (16) 建立在不变子空间 W{1,x} 上的广义分离变量解是

v(x,t)=c1(t)+c2(t)x。

其中c1(t),c2(t)满足下面的二维动力系统

由变换 v=f(u)=b3sinu+b4cosu 得到方程

ut=[D(u)ux]x+Q(u)

有广义泛函分离变量解

其中

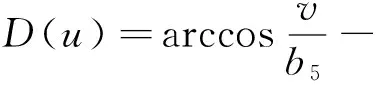
Q(u)=(c1(t)+c2(t)x)(b3cosu-b4sinu)，

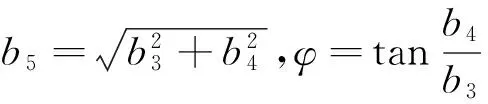
c1(t),c2(t)满足上面的二维动力系统。

例2方程

允许的二阶条件Lie-Bäcklund对称是

此方程在不变子空间 W{1,x2} 上有广义变量分离解

v(x,t)=c1(t)+c2(t)x2。

其中c1(t),c2(t)满足下面的二维动力系统

由变换

得方程

ut=[D(u)ux]x+g(x)Q(u)

有广义泛函分离变量解

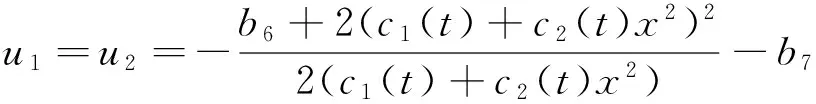
其中

D(u)=2(c1(t)+c2(t)x2)2,

c1(t),c2(t)满足上面的二维动力系统。

4　结　语

本文用条件Lie-Bäcklund对称方法对一类在物理学中有重要应用的广义非线性反应扩散方程进行了分类, 研究方程(1)的非线性条件Lie-Bäcklund对称(11)等价于研究该方程由变换v=f(u)而得的新方程(12)的线性条件Lie-Bäcklund对称(13)。由σ=0和相应方程的相容性构造了分类方程定义在由σ=0定义的不变子空间上的广义分离变量解。这些结果可由变换v=f(u)转换为非线性扩散方程允许的非线性条件Lie-Bäcklund对称η及其泛函广义分离变量解。 同时, 这些解可以用来刻画方程的爆破熄灭等奇性以及长时间行为等性态。

[1]FOKAS A S, LIU Q M. Nonlinear interaction of traveling waves of nonintegrable equations [J]. Physical Review Letters, 1994, 72(21): 3293-3296.

[2]JI L N. Condition Lie-Bäcklund symmetries and functionally generalized separable solutions to the generalized porous medium equations with source [J]. Journal of Mathematical Analysis and Applications, 2012, 389(2): 979-988.

[3]GALAKTIONOV V A, SVIRSHCHEVSKII S R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].London: Chapman and Hall/CRC, 2007.

[4]ZHDANOV R Z. Conditional Lie-Bäcklund symmetry and reductions of evolution equations [J]. Journal of Physics. A. Mathematical and theoretical, 1995, 28(13): 3841-3850.

[5]SVIRSHCHEVSKII S R. Lie-Bäcklund symmetries of linear ODEs and generalized separation of variables in nonlinear equations [J]. Physics letters A, 1995, 199(56): 344-348.

[6]QU C Z, JI L N, WANG L Z. Conditional Lie-Bäcklund symmetries and sign-invariants to quasi-linear diffusion equations [J]. Studies in Applied Mathematics, 2007, 119(4): 355-391.

[7]JI L N, QU C Z. Conditional Lie-Bäcklund symmetry and invariant subspace to nonlinear diffusion equation [J]. IMA Journal of Applied Mathematic, 2011, 76(4): 610-632.

[8]万晖, 带源项的变系数非线性反应扩散方程的精确解[J]. 物理学报, 2013, 62(9): 1-9.

[9]CHERNIHA R, PLIUKHIN O. New conditional symmetries and exact solutions of nonlinear reaction-diffusion-convection equations[J]. Journal of Physics A: Mathematical and Theoretical, 2007, 40(33):1049-1070.

(编辑亢小玉)

Invariant subspace and conditional Lie-Bäcklund symmetries of the generalized nonlinear diffusion equation

XIA Ya-rong1,2

(1.School of Mathematics, Northwest University, Xi′an 710127, China; 2.School of Information and Engineering, Xi′an University, Xi′an 710065， China)

In this paper, invariant subspace approach and conditional Lie-Bäcklund symmetries are used to research the generalized nonlinear diffusion equations. It is shown that the equation admits a class of invariant subspaces, which is equivalent to a kind of higher-order conditional Lie-Bäcklund symmetries of the equation. Finally, two examples are given and the generalized functional separable solutions to the equation are constructed.

nonlinear diffusion equation; invariant subspace; conditional Lie-Bäcklund symmetries; generalized functional separable solution

2015-06-10

国家自然科学基金资助项目(11371293)；陕西省自然科学基础研究计划基金资助项目(2014JM2-1009)；西安市科技计划“文理专项”基金资助项目(CYX1531WL41)

夏亚荣，女，陕西西安人，博士生,从事偏微分方程研究。