一类广义扰动振子共振机制的同伦映射近似解

许永红，石兰芳，莫嘉琪

(1.蚌埠学院 数理系, 安徽, 蚌埠　233030；2.南京信息工程大学 数学与统计学院, 江苏 南京　210044;3.安徽师范大学 数学系, 安徽 芜湖　241003)



一类广义扰动振子共振机制的同伦映射近似解

许永红1，石兰芳2，莫嘉琪3

(1.蚌埠学院 数理系, 安徽, 蚌埠233030；2.南京信息工程大学 数学与统计学院, 江苏 南京210044;3.安徽师范大学 数学系, 安徽 芜湖241003)

为研究一类广义扰动方程，先求得了相应的线性方程的解， 然后利用泛函分析映射原理得到了广义扰动振子随机共振机制的渐近解, 并论述了解的一致有效性态。

泛函映射子; 共振机制; 渐近解

扰动振子的共振在自然界中广泛存在。1989年开始, 许多学者对随机共振进行了系统研究[1]。2003年, 研究了随机振子的微弱信号的检测系统[2], 并讨论了高维振子的信号、噪声和非线性系统三者之间的匹配。但在实际中, 信号和噪声情况往往未知, 并且它们与系统三者之间也不总是最优的匹配。在文献[3]中, 提出了变尺度随机共振, 研究了大频率信号的随机共振。建立了广义的调参随机共振的较一般的研究方法[4]。

由于非线性奇异摄动微分方程的解一般不能用有限项的初等函数来描述。因此，需用近似的求解方法来求非线性方程的近似解析解。作者等也利用各种渐近和近似方法来求得相应的非线性方程的近似解[5-24]。本文是用经过改进的泛函分析同伦映射方法得到广义扰动方程共振机制的渐近解。

1　广义扰动方程共振机制

研究下列广义扰动方程初值问题:

Acos(2πω t)+Cg(t),

(1)

y|t=0=h1,

(2)

(3)

其中-au+bu3为势场作用力; Cg(t)是噪声信号; k为阻尼系数; Acos(2πω t)是振子的周期驱动力; C, h1, h2为常数, g(t)表示Gauss白噪声函数, 设它是充分光滑的有界函数。方程(1)可以看作Brown粒子在液体等介质的势场中的运动。其中系统输出y(t)是Brown粒子的位移函数。

2　泛函同伦映射

为了求得广义扰动共振机制方程(1)的渐近解。现构造如下泛函同伦映射H[y,p]∈[R, [0,1]]:

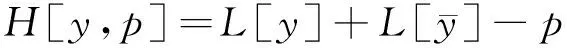
(4)

由泛函分析同伦映射(4)知,H(u, 1)=0就是非线性扰动共振机制方程(1), 因此仅需选择在相同的初始条件和边值条件(2)和(3)式下, 广义扰动方程初值问题(1)～(3)的解就是H(u,p)=0的解取极限p→1的情形的解。

考虑方程(1)所对应的线性问题:

(5)

[Acos(2πωυ)+Cg(τ)]dτ。

(6)

将解y(t)展开为p的幂级数:

(7)

将式(7)代入泛函同伦映射(4), 合并pi的同次幂的项, 令各次幂的系数为零。由p0的系数可得

(8)

[Acos(2πωυ)+Cg(τ)]dτ。

(9)

将式(7)代入泛函同伦映射(6), 合并pi的同次幂项。由p1的系数，可得

(10)

因此方程(10)在零初始条件下的解为

(11)

其中y0由式(9)所示。

再由式(9), (11), 并在式(7)中取p=1, 可得广义非线性扰动共振机制无量纲模型(1)～(3)的一次近似解析解Y1(t):

(12)

将式(7)代入泛函同伦映射(6), 合并pi的同次幂项。由p2的系数

(13)

可得方程(12)在零初始值下的解为

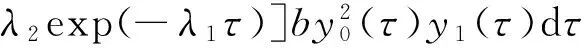
(14)

其中y0,y1分别由式(9), (11)表示。

再由式(9), (11), (14), 并在式(7)中取p=1, 得到广义非线性扰动模型(1)～(3)的二次近似解析解Y2(t):

Y2(t)=y0(t)+y1(t)+y2(t)=

λ2exp(-λ1τ)]×

[Acos(2πωυ)+Cg(τ)-

(15)

式(15)中y0,y1分别由式(9), (11)表示。

继续将式(7)代入泛函映射式(6), 合并pi的同次幂项。由pk(k=3,4,…)的系数

L[yk]=Gk，k=3， 4，…，

(16)

其中

为逐次已知的函数。

方程(16)在零初始边值下的解为

λ2exp(-λ1τ)]Gk(τ)dτ。

(17)

由式(9), (11), (13), (17), 并在式(7)中取p=1, 可得到广义非线性扰动模型(1)～(3)的第k次近似解析解Yk(t):

Yk(t)=y0(t)+y1(t)+y2(t)+…+yk(t)=

λ2exp(-λ1τ)]×

(18)

因此进一步可得

Y(t)=y0(t)+y1(t)+y2(t)+…+

yk(t)+…=

λ2exp(-λ1τ)]×

(19)

我们可用泛函分析理论的不动点原理和逐次逼近理论证明[25-26]: 由式(19)表示的解Y(t)关于t是一致收敛的, 并且它为广义扰动共振机制方程初值问题(1)～(3)的精确解。

3　举　例

(20)

由式(9), 对应的广义扰动共振机制方程(20)的初始迭代y0为

Y0(t)=y0(t)=

(2sint-cost)exp(-t)]。

(21)

由式(11), 得到y1(t):

(22)

再由式(12), 可得广义扰动共振机制方程(20)的一次近似解Y1:

(2sint-cost)exp(-t)]-

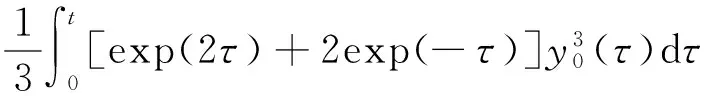
(23)

其中y0由式(21)表示。

由式(13), 可得到y2(x):

(24)

再由式(15), 得到广义扰动方程(20)的二次近似解Y2:

(2sint-cost)exp(-t)]-

(25)

用同样的方法，可依次地得到广义扰动共振机制方程(20)的更高次的近似解Yk(t)(k=3,4,…)。

由于近似解函数序列{Yn(t)}关于t是一致收敛的函数序列。因此当n→∞时, 广义扰动方程(20)渐近解Yn(t) 随n的增大而越来越接近精确解Y(t)。

4　随机共振机制解的物理解释

由泛函分析同伦映射方法得到的广义扰动函数序列方程的近似解Yn(t), 因此还可对近似解析解通过解析运算继续对随机共振机制进一步研究, 得到相关的其他物理性态。

此外, 还可利用渐近解Yn(t)通过解析方法来讨论势场作用力的计算、 噪声强度的变化对随机共振的影响、 逃逸速率参数的分析、 以及各调节系统参数的最优匹配等物理性态。

5　结　语

泛函分析同伦映射的渐近方法, 若选取选定合适的初始函数, 能较快速地得到渐近解析解, 并利用解析运算来进一步研究对应物理模型的其他相关物理性态。

[1]康艳梅, 徐健学, 谢勇.弱噪声极限下二维布朗运动的随机共振现象[J].物理学报, 2003, 52(4):802-808.

[2]WANGFZ,CHENWS,QINGR,etal.Experimentalanalysisofstochasticresonanceinaduffingsystem[J].ChinPhysLett,2003,20(1):28-30.

[3]冷永刚, 赖志慧, 范胜波,等.二维Duffing振子的大参数随机共振及微弱信号检测研究[J].物理学报, 2012, 61(23):230502.

[4]冷永刚, 赖志慧.基于Kramers逃逸速率的Duffing振子广义调参随机共振研究[J].物理学报，2014, 63(2): 020502.

[5]MOJia-qi.Aclassofsingulaelyperturbeddifferential-differencereactiondiffusionequations[J].AdvMath, 2009, 38 (2): 227-230.

[6]MOJia-qi，LINWan-tao.Asymptoticsolutionofactivatorinhibitorsystemsfornonlinearreactiondiffusionequations[J].JSysSci&Complexity, 2008, 20 (1): 119-128.

[7]MOJia-qi.ApproximatesolutionofhomotopicmappingtosolitaryforgeneralizednonlinearKdVsystem[J].ChinPhysLett, 2009, 26 (1):010204-1-010204-4.

[8]MOJia-qi.AvariationaliterationsolvingmethodforaclassofgeneralizedBoussinesqequations[J].ChinPhysLett, 2009, 26 (6): 060202-1-060202-3.

[9]MOJia-qi.Homotopicmappingsolvingmethodforgainfluencyoflaserpulseamplifier[J].ScienceinChina,SerG, 2009, 39 (5): 568-661.

[10]MOJia-qi，LINWan-tao.Asymptoticsolutionforaclassofsea-airoscillatormodelforEl-Nino-southernoscillation[J].ChinPhys, 2008, 17 (2):370-372.

[11]MOJia-qi.AclassofhomotopicsolvingmethodforENSOmpdel[J].ActaMathSci,2009, 29(1):101-109.

[12]MOJia-qi，CHENHuai-jun.ThecornerlayersolutionofRobinproblemforsemilinearequation[J].MathAppl, 2012, 25(1):1-4.

[13]MOJia-qi,LINYi-hua,LINWan-tao,etal.Perturbedsolvingmethodforinterdecadalsea-airoscillatormodel[J].ChinGeographicalSci, 2012, 22 (1):42-47.

[14] 许永红, 石兰芳, 莫嘉琪.强阻尼广义Sine-Gordon方程特征问题的变分迭代法[J].物理学报, 2015, 64(1)：010201.

[15] 许永红, 韩祥临, 石兰芳,等.薛定谔扰动耦合系统孤波的行波近似解法[J].物理学报, 2014, 63(9)：090304.

[16] 许永红, 林万涛, 温朝晖,等.一类燃烧问题的奇摄动解[J].武汉大学学报(理学版), 2013, 59(3): 239-241.

[17] 许永红, 林万涛, 徐 惠, 等.一类相对论转动动力学模型[J].兰州大学学报(自然科学版), 2012, 48(1): 100-103.

[18] 许永红, 姚静荪, 莫嘉琪.(3+1)维Burger扰动系统孤波的解法[J].物理学报, 2011，61(2): 020202.

[19] 许永红, 温朝晖, 徐惠, 等.扰动Benjamin方程物理模型的孤波解[J].吉林大学学报(理学版), 2011，49(4): 659-663.

[20] 许永红, 温朝晖, 莫嘉琪.扰动mKdV耦合系统的孤子解[J].物理学报,2011，60(5): 050205.

[21] 许永红, 温朝晖, 莫嘉琪.一类Lorenz系统的变分迭代解法[J].吉林大学学报(理学版), 2011，49(1): 51-55.

[22] 石兰芳, 陈贤峰, 韩祥临, 等.一类Fermi气体在非线性扰动机制中轨线的渐近表示[J].物理学报,2011，63(6): 060204.

[23]LIAOShi-jun.BeyondPerturbation:IntroductiontotheHomotopyAnalysisMethod[M].NewYork:CRCPress, 2004.

[24] 何吉欢.工程和科学中的近似非线性分析方法[M].郑州：河南科学技术出版社，2002.

[25]BARBUL,MOROSANUG.SingularlyPerturbedBoundary-ValueProblems[M].Basel:BirkhausermVerlagAG, 2007.

[26]DEJAGEREM,FURUJ.TheTheoryofSingularPerturbation[M].Amsterdam:North-HollandPublishingCo, 1996.

(编辑亢小玉)

The approximate solution of homotopic mapping to a class of generalized disturbed oscillator for resonance mechanism

XU Yong-hong1, SHI Lan-fang2, MO Jia-qi3

(1.Department of Mathematics & Physics, Bengbu College, Bengbu 233030, China; 2.College of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing 210044, China; 3.Department of Mathematics, Anhui Normal University, Wuhu 241003, China)

A class of nonlinear generalized disturbed equation was considered. Firstly, the corresponding nonlinear problem solves exact solutions. Then asymptotic solutions for nonlinear disturbed oscillator for the resonance mechanism was obtained using the mapping principle of functional analytic, and the uniform validity was proved.

mapping principle of functional analytic; resonance mechanism; asymptotic solution

2015-04-13

国家自然科学基金资助项目(11202106)；浙江省自然科学基金资助项目(LY13A010005)；安徽省高等学校省级自然科学研究基金资助项目(KJ2014A151)

许永红，女，江苏兴化人，教授,从事物理学、数学物理研究。

O175.14

ADOI：10.16152/j.cnki.xdxbzr.2016-01-004