基于柔性支撑的风机传动链动态特性研究

张盛林，朱才朝，宋朝省，黄华清

(重庆大学 重庆大学机械传动国家重点实验室，重庆　400030)



基于柔性支撑的风机传动链动态特性研究

张盛林，朱才朝，宋朝省，黄华清

(重庆大学 重庆大学机械传动国家重点实验室，重庆400030)

为了获得高空的风力资源，风力发电机组大多安装在100 m的塔架上，在变风向与变载荷等恶劣工况共同作用下，塔架的柔性使得风机传动链受力变形复杂，成为风机的薄弱环节。以三点支撑风电机组为研究对象，将塔架考虑成柔性体，利用有限元法提取支撑塔架三个支撑接合部处参数，建立基于柔性支撑风机传动链耦合动力学模型，得到传动链的固有特征。其第一阶次和第二阶次固有频率分别对应塔架的摆振和传动链的扭振，利用坎贝尔图得到传动链的潜在共振频率，通过计算模态能量，对潜在共振点进行识别，得出1.55 Hz为传动链的潜在共振频率。通过风场在线监测，跟踪风机主轴振动随转速的变化规律，实测风机传动链共振频率为1.56 Hz，理论计算结果与实验结果基本一致，误差约为1%。

风电机组；传动链；动态特性；柔性支撑；耦合分析

风力发电机组分为水平轴式和竖直轴式两种类型，其中又以水平轴式风电机组为主。水平轴风电机组的共同点为从叶片到主轴，再到齿轮箱的整个风机传动链都是利用主轴轴承以及齿轮箱的左右扭力臂作为支撑，最后安装在风机塔架的顶端。由于塔架较高，柔性较大，在风场复杂多变的风载下，传动链的受载必定导致塔架的变形，而风机塔架的变形又会使得风机传动链受力变形更为复杂，进而导致传动链故障高发，成为了风电机组的薄弱环节。

目前国内外学者对风电机组传动系统进行了一定的研究。ZHU等[1-2]通过考虑实测载荷普和齿轮时变啮合刚度对风机传动链进行了分析，同时以齿轮啮合原理和齿轮系统动力学等为依据，考虑齿轮时变刚度和误差的基础上对风机齿轮箱进行了研究。陈会涛等[3]考虑齿轮综合传递误差等因素，建立了风机行星轮纯扭转模型，研究了传递误差随机波动对风机齿轮系统动力学特性的影响3。徐向阳等[4]综合考虑行星轮传动时变啮合刚度与时变啮合误差，研究了柔性销轴刚度和误差对行星轮均载的影响。PEETERS等[5]使用有限元法对风机增速箱固有特性和动态响应特性进行了研究。KAHKAMAN等[6-9]对风电齿轮箱系统动力学特性进行了研究。综上所述现有研究主要集中于对传动链或传动链中的部件进行研究，而还没有文章研究风场现场塔架对风机传动链的影响。

通过考虑风机塔架对传动链的柔性支撑，采用集中参数法建立传动链动力学模型，利用有限元法建立塔架动力学模型，通过结合部的耦合矩阵等参数将传动链与塔架相互耦合，根据此模型对风机传动链的动态特性进行研究，为传动链设计提供参考，具有重要的理论意义与工程应用价值。

1　风机传动链构成与传动原理

为了获得高空的风能资源，风机传动链通常通过塔架支撑在高空中，风机发电功率越大，塔架高度相对越高，而塔架的柔性也就越大。水平轴式风机结构如图1(a)所示，叶片根部通过变桨装置与轮毂连接，轮毂通过法兰盘与主轴固定连接，主轴通过锁紧盘与增速齿轮箱的行星架连接的同时由主轴轴承支撑在机舱上，增速齿轮箱通过左右两个扭力臂固定在机舱里，同时增速齿轮箱的高速轴通过联轴器与发电机转子相连。根据致动盘等相关理论，叶片前后的气压差在驱动叶片旋转的同时将风能转换为机械能，机械能依次通过轮毂、主轴、增速齿轮箱和联轴器传递到发电机处，最终将风能转换为电能。文中将风机考虑为传动子系统与支撑塔架子系统。传动链子系统由叶片、轮毂、主轴、增速箱、联轴器等构成；支撑子系统由塔筒和机舱构成。其中传动链模型和支撑模型通过主轴轴承(图1(a)中A点)、增速齿轮箱左右扭力臂(图1(a)中B/C点)三点支撑相互连接。根据风机模型图，可以得到如图1(b)所示的风机拓扑关系连接图，虚线框内分别为传动链子模型和支撑塔架模型拓扑关系图。图中KB1、KF1和KF2分别对应主轴轴承、增速齿轮箱左扭力臂和增速齿轮箱右扭力臂与塔架接洽部。

图1　典型风机结构简图及其拓扑关系图Fig.1　Structure and topology of typical wind turbine

符号名称符号名称BL叶片CP联轴器HB轮毂CB机舱MS主轴TW塔筒GR发电机转子KB轴承刚度与阻尼KS扭转刚度与阻尼KF支撑刚度与阻尼GB齿轮箱

风机传动链中增速齿轮箱是较为重要而又复杂的部件，同时也是风机内部激励的主要来源，文中考虑增速齿轮箱的行星级、中间级和高速级各齿轮与轴等主要机械传动部件。图2(a)所示为典型增速齿轮箱结构简图，其锁紧盘与主轴相连为扭矩输入端，高速轴与联轴器相连为扭矩输出端，齿圈固定在箱体上。增速齿轮箱拓扑关系连接图如图2(b)所示，行星架上的锁紧盘与主轴连接，行星轮安装在行星架上，与齿圈啮合的同时又与太阳轮进行啮合传动，此为第一级增速。此后通过两级平行级齿轮啮合进行第二级和第三极增速。

图2　增速齿轮箱结构及拓扑关系图Fig.2　Structure and topological of gearbox

符号名称符号名称c行星架Tin输入扭矩p行星轮Tout输出扭矩r行星架Si(i=1,2,3)低/中/高速轴s太阳轮g1/g2中间级主/从动轮k啮合刚度sp行星轮轴b轴承g3/g4高速级主/从动轮

2　基于柔性支撑风机传动链耦合动力学建模

如图3所示，传动链子模型与支撑塔架子模型通过三点支撑处结合部的力和位移关系以及耦合刚度矩阵要素进行耦合。在主轴轴承和扭力臂三点通过无质量弹簧代替其相互作用力，每个点考虑三个平移和三个转动自由度。

图3　基于柔性支撑风机传动链耦合动力学建模Fig.3　Dynamic coupling model of wind turbine drive train with flexible supporting

单独取出主轴轴承位置的6个自由度，以Xm表示主轴的位移矢量，则主轴动力学方程可表示为：

(1)

式中:Mm,Km,Cm,Fm分别为主轴的广义质量矩阵、刚度矩阵、阻尼矩阵和力矢量。

以Xb1表示弹簧一端(Mb1=0)的位移矢量，则弹簧Mb1=0端的动力学方程可以写为如下形式：

(2)

式中:Mb1,Kb1,Cb1,Fb1分别为Mb1的广义质量矩阵、刚度矩阵、阻尼矩阵和力矢量。

根据式(1)、式(2)将弹簧Mb1端与主轴进行动力学耦合，得到如下主轴-弹簧耦合方程：

(3)

式中:Kmb1,Cmb1为弹簧与主轴的耦合刚度矩阵和阻尼矩阵。Kmb1,Cmb1是两个子模型进行动力学耦合的主要参数。Kmb1计算方法为：在耦合点各单一自由度上施加单位载荷，通过测量耦合点在所有自由度上的变形，即可计算Kmb1。其推导步骤如下：

[Kmb1]6×6[δmb1]6×6=[FⅠ]6×6

(4)

式中:[δmb1]6×6为耦合点位移矩阵；[FⅠ]6×6为单位载荷矩阵。

(5)

同样，使弹簧另一端(Mb2=0)与支撑塔架进行耦合，可以得到如下支撑塔架-弹簧的耦合方程：

(6)

式中:Mb2,Kb2,Cb2,Fb2分别为弹簧的广义质量矩阵、刚度矩阵、阻尼矩阵和力矢量。ktb2,Ctb2为弹簧与塔架之间各自由度的耦合刚度矩阵和阻尼矩阵。Ktb2计算方式同前诉述。

由于弹簧无质量(Mb1=Mb2=0)，且两端作用力大小相同方向相反(Fb1=-Fb2)，因此根据式(3)和式(6)可以得到主轴-弹簧-塔架相互耦合的动力学方程，如下所示：

酒店提供的产品主要表现为综合性的服务，而这种“产品”的实现方式又是多样化、多环节的，在内容上有着极大的不确定性和灵活性，因此也就很容易产生管理上的漏洞，所以我们要针对酒店出现的一系列生产管理上的漏洞而进行内部控制，所谓内部控制，即是企业为了保护财产的安全与完整，检查会计资料的准确性和可靠性，提高企业的经营效率和促进企业贯彻既定的经营方针所设计的总体计划以及所采取的与总体计划相适应的一切方法和措施。

(7)

使用同样的方法可以得到两个扭力臂与塔架相互耦合的动力学方程。

综上，基于柔性支撑的风机传动链动力学方程可表示为如下形式：

(8)

传动链子模型包括叶片、主轴、齿轮箱、发电机等，利用集中参数法建立传动链子系统动力学模型[10-15]：

(9)

在建立支撑子系统动力学模型时将机舱考虑为塔架顶端一个刚性点，由于塔架结构较为复杂，此处忽略塔架中的法兰盘等较小的结构，将塔架考虑为变厚变直径圆筒，圆筒使用四节点六自由度壳单元进行有限元离散化处理，。根据虚功原理获得如下质量矩阵、刚度矩阵和阻尼矩阵：

(10)

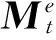
将式(9)和式(10)中得到的广义质量矩阵、刚度矩阵和阻尼矩阵代入式(8)，可得完整的分析模型。

3　基于柔性支撑风机传动链动态特性分析

本文以某兆瓦级风电机组为例，表3和表4分别为风电机组的基本参数和齿轮箱基本参数。

表3　风机基本参数

表4　齿轮箱基本参数表

依据表3和表4等风机相关参数，建立模型并求解模型，提取系统前15阶固有频率ωi和对应振型Φi如下表5所示，其中前6阶固有振型如图4所示。系统前6阶固有振型中有4阶的主阵型为塔筒的摆动或者扭振。其第一阶为塔筒的横向摆动，当风机受到外部激励导致塔筒发生横向摆动后，会使得整个传动链在产生较大横向位移的同时又产生倾斜，因此使得传动链上部件的受力状态发生较大改变,导致传动链上的力分配变得复杂，其中主轴轴承轴向力的幅值随着塔筒位移增大而明显增大，其垂直方向力的幅值随着塔筒位移增大而明显减小，其水平方向力的方向随着塔筒横向摆动而发生明显波动，从而影响传动链部件的工作性能与寿命，进而增加传动链的故障率。

表5　系统固有频率和阻尼比

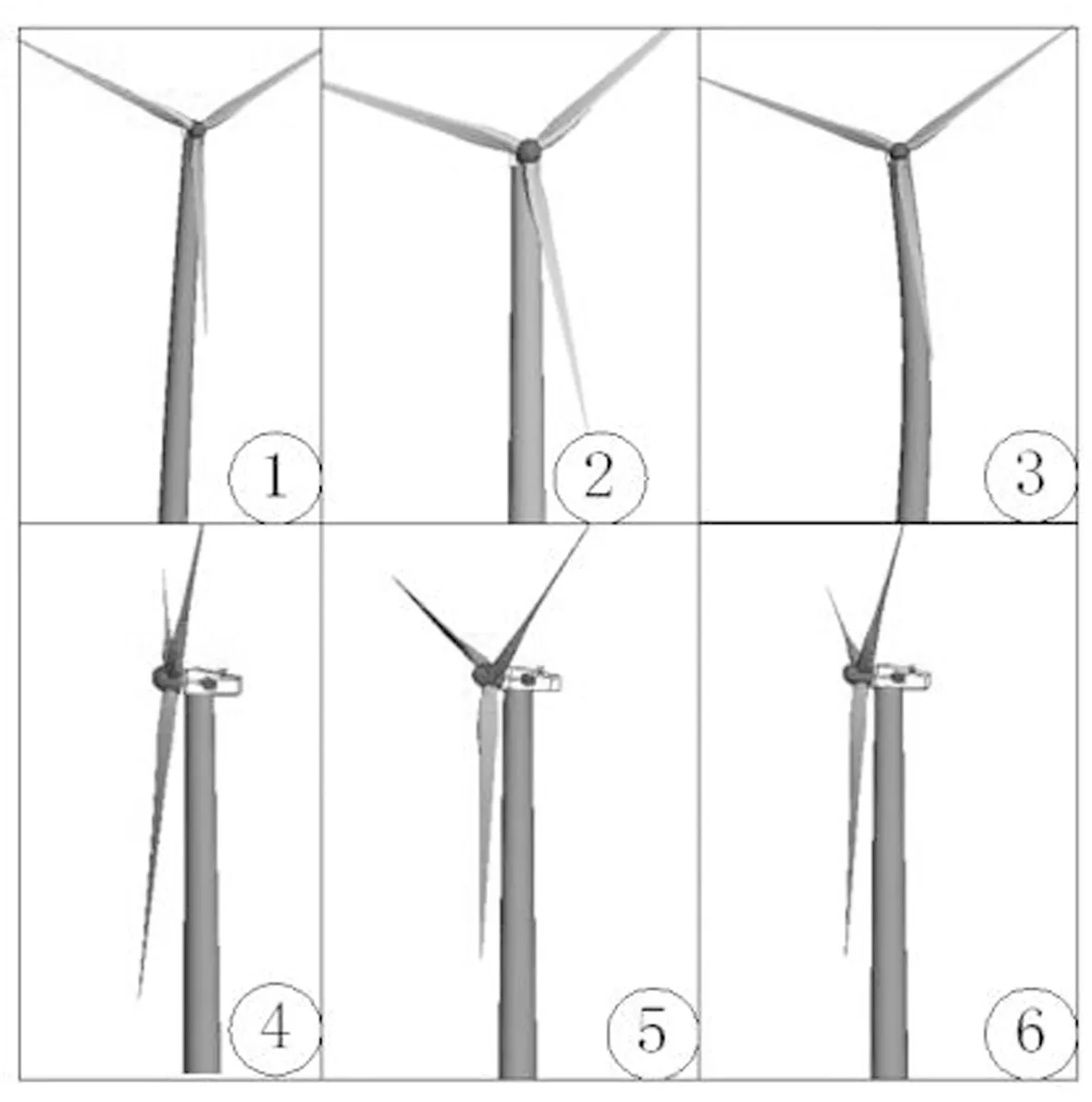
图4　系统前六阶固有振型Fig.4　First six-order mode shapes

转速切入转速额定转速切出转速1050r/min1790r/min1900r/pinMss_1p0.15180.2590.275Mss_2p0.3040.5180.55Mss_3p0.4560.7770.824Mss_6p0.9111.551.645Lss_1p0.8461.441.53Lss_2p1.692.883.06Iss_1p3.576.086.46Iss_2p7.1412.1712.91Hss_1p17.529.8331.67Hss_2p3559.6763.3Lsm_1p14.5830.2926.38Lsm_2p29.1560.5752.76Ism_1p82.06139.90148.50Ism_2p164.13279.80296.99Hsm_1p367.5686.17665Hsm_2p73512531330

注：“Mss”为主轴转频，“Lss”为低速轴转频，“Iss”为中间轴转频，“Hss”为高速转频，“Lsm“为低速级啮合频率，“Ism“为中间级啮合频率，“Hsm“为高速级啮合频率，“_ip”为第i倍频率。

为了得到激励频率与固有频率的交点，依据表5和表6得到如图5所示Campbell图，图中“Mode ip”代表系统的第i阶固有频率。为了尽可能显示清楚每一阶次固有频率，将Campbell图分为三段分别画出，如图5中(a)、(b)、(c)所示。

从图5系统Campbell图中可以看出，在系统前15阶固有频率范围内共存在15个潜在共振点。表7为各潜在共振点对应的固有频率与激励频率。

图5　系统Campbell图Fig.5　Campbell diagrams of the system

编号频率/Hz激励频率/HzA0.37主轴转频2pB1.55主轴转频6pC2.3低速轴转频2pD3.88中间轴转频1pE7.59中间轴转频2pF11.51中间轴转频2pG19.03低速轴啮合频率1pH19.03高速轴转频1pJ32.87低速轴啮合频率2pK39.51低速轴啮合频率2pL39.51高速轴转频2pM110.8中间级啮合频率1pN641.4高速级啮合频率1pO1165高速级啮合频率2p

振动强度与模态能量密切相关，高模态能量预示着当系统受到激励后会产生较大的振动，因此使用模态能量法对潜在共振点进行识别。根据能量法：若某潜在共振点所在阶次的某一个部件能量占有比大于20%，同时此部件为此共振点的激励频率，则可以进一步说明其为潜在共振点，否则不为共振点。多自由度系统第n阶模态第i个部件的动能和第n阶模态的总动能分别为：

(12)

(13)

式中：ωn为统第n阶固有圆频率；(Φn)i为部件i第n阶振型向量；Mi为部件i广义质量矩阵；Φn为系统第n阶振型向量；M为系统广义质量矩阵

各部件的模态能量占有百分比可定义为：

(14)

图6所示为根据式(14)得到的系统前6阶模态能量分布图，表8为其余9阶中模态能量占有比大于20%的部件统计表。

表8　系统7-15阶模态能量主要分布表

因为叶片、轮毂和主轴为同一转频，再结合Campbell图、各阶能量分布图及分布表可以看出，仅B点满足能量法的要求，为系统的潜在共振点。图6(b)表明，三片叶片的能量之和共占据第二阶固有频率模态总能量的70%以上，同时其转频6倍频与第二阶固有频率存在交点。

图6　前六阶模态能量分布图Fig.6　The first six orders modal energy distribution

4　实验验证

为了进一步验证B点是否为传动链的共振点，对风场的风机进行了振动测试，因为其模态能量主要分布在叶片和高速轴上，而叶片处于机舱外部，不便于对叶片进行直接测试。由于叶片是与轮毂连接，轮毂固定在主轴上，叶片的共振势必会使得主轴的振动加剧，因此综合考虑改为测试主轴的振动。测试方法如图7左侧所示，在风机主轴轴承的垂直方向(y向)安装加速度传感器，测试主轴振动加速度；在风机高速轴安装光电转速传感器，测试风机转速。通过数据收集模块WindCon同时收集主轴振动数据和高速轴转速数据，并存放与计算机当中。加速度传感器和转速传感器现场安装情况如图7右上角所示，数据采集模块和存模块如图7右下角所示。

图7　现场传感器布置图Fig.7　Installation of sensors on the wind turbine

测试过程中采集到了转速从风机启动到风机切出风速的转速范围，结果显示在风机从1 646 r/min升速到1 810 r/min的过程中主轴y向振动频谱图中有1.56 Hz的频率出现，且幅值较大，图8为其加速度振动时域图，图9为图8中前0.1 s的的放大图，图10为图8中的时域曲线经过10 Hz的低通滤波图，图12为图8振动加速度的FFT图。

图8　主轴加速度振动曲线Fig.8　The acceleration curve of main shaft

图9　主轴加速度振动曲线Fig.9　The acceleration curve of main shaft

图10　主轴加速度低通滤波曲线图Fig.10 Low-pass filter curve of acceleration of main shaft

图11　主轴加速度振动频谱图Fig.11 The acceleration spectrum of main shaft

通过观察实验测试结果，发现风机转速在1 700 r/min左右时，振动频谱图中有1.56 Hz的峰值突然显得较为突出，例如转速为1 664 r/min时，频谱图中主要频率成分为高速级啮合频率和中间级啮合频率以及边频，当转速升到1 691 r/min的时频谱图中1.56 Hz处的峰值明显升高，达到了17.7 m/s2，与高速级的啮合频率峰值持平；当转速升高到1 782 r/min时，频谱图中1.56 Hz的峰值明显降低；当转速升高到1 810 r/min时，频谱图中1.56 Hz的频率峰值基本消失。分析原因为：随着风机转速在一定范围内增加，叶片-轮毂-主轴的6倍频(激励频率)距离系统的固有频率较远，固有频率未被激发，因此频谱图中无1.56 Hz峰值出现；然后此激励频率逐渐靠近系统固有频率并产生交点，使得固有频率被激发，因而出现较大的振动峰值；最后激励频率远离此阶次固有频率，频率峰值消失。在试验分析过程中的转速和峰值频率与理论分析中Campbell图上B点的转速和固有频率基本一致。此结果表明，试验分析模型与理论计算模型基本一致，因此验证了分析模型的正确性。

5　结　论

论文以典型的三点支撑风电机组为研究对象，将风机模型分为支撑塔架和传动链两个子模型，将塔架考虑为柔性体，利用有限元法提取了支撑塔架三个支撑部位的参数，建立了基于柔性支撑的风机传动连耦合动力学模型，通过求解系统动力学方程对风电机组的固有特性进行了研究：

(1)提取了系统的前15阶固有频率和前6阶振型。其第一阶固有频率(0.37 Hz)为塔筒的横向摆动，此横向摆动容易导致传动链发生横向位移和倾斜，从而使得传动链上的构件受力变得复杂，影响部件的工作性能和寿命等。

(2)利用Campbell对风电机组进行了潜在共振分析，共得到了15个潜在共振点，同时通过能量法，排除了其中14个为共振点的可能性。

(3)为了进一步验证系统第二阶固有频率(传动链扭振)与叶片-轮毂-主轴转频的6倍频交点是否为共振点，对风场风机进行了监测，观测到了在风机转速通过特定范围时，随风机转速的升高，主轴振动频谱图中某一频率出现了从无到较大值再到无的过程，验证了1.55 Hz为传动链的共振频率，进而说明试验结果与理论结果的一致性。

[1]ZHU C,CHEN S,LIU H,et al.Dynamic analysis of the drive train of a wind turbine based upon the measured load spectrum[J].Journal of Mechanical Science & Technology,2014,28(6):2033-2040.

[2]朱才朝,黄泽好,唐倩,等.风力发电齿轮箱系统耦合非线性动态特性的研究[J].机械工程学报,2005,41(8):203-207.

ZHU Caichao,HUANG Zehao,TANG Qian，et al.Analysis ofnonlinear coupling dynamic characteristics of gearbox system about wind-driven generator[J].Journal of Mechanical Engineering,2005,41(8):203-207.

[3]陈会涛,秦大同,吴晓铃,等.考虑随机制造误差的风力机行星齿轮系统动力学特性[J].机械工程学报,2012,48(21):77-83.

CHEN Huitao,QIN Datong,WU Xiaoling.et al.Dynamic characteristics of planetary gear transmission system of wind turbine with random manufacturing error[J].Journal of Mechanical Engineering,2012,48(21):77-83.

[4]徐向阳,朱才朝,刘怀举,等.柔性销轴式风电齿轮箱行星传动均载研究[J].机械工程学报,2014,50(11):43-49.

XU Xiangyang,ZHU Caichao,LIU Huaiju.et al.Load sharing research of planetary gear transmission system of wind turbine gearbox with flexible pins [J].Journal of Mechanical Engineering,2014,50(11):43-49.

[5]PEETERS J,VANDEPITTE D,SAS P,et al.Comparison of analysis techniques for the dynamic be-haviour of an integrated drivetrain in a wind turbine[J].International Conference on Noise and Vibration Engineering location:Leuven,Belgium date:Sep-2002.

[6]KAHRAMAN A.Planetary gear train dynamic[J].Journal of mechanical design,1994,116(3):713-720.

[7]PARKER R G,AGASHE V,VIJAYAKAR S M.Dynamic response of a planetary gear system using a finite element/contact mechanics model[J].Journal of Mechanical Design,2000,122(3):304-310.

[8]PARKER R G.A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J].Journal of Sound & Vibration,2000,236(4):561-573.

[9]PEETERS J L,VANDEPITTE D.Analysis of internal drive train dynamics in a wind turbine[J].Wind Energy,2006,9(1/2):141-161.

[10]HELSEN J,VANHOLLEBEKE F,MARRANT B,et al.Multibody modelling of varying complexity for modal behaviour analysis of wind turbine gearboxes[J].Renewable Energy,2010,36(11):3098-3113.

[11]张盛林,宋朝省,翟洪飞,等.兆瓦级风电机组传动链动态特性分析[J].重庆大学学报,2015(1):12-19.

ZHANG Shenglin,SONG Chaosheng,ZHAI Hongfei,et al.Dynamic characteristics analysis of megawatt wind turbine drive train [J].Journal of Chongqing University,2015(1):12-19.

[12]邱星辉,韩勤锴,褚福磊.风力机行星齿轮传动系统动力学研究综述[J].机械工程学报,2014,50(11):23-36.

QIU Xinghui,HAN Qinkai,CHU Fulei.Review on dynamic analysis of wind turbine geared transmission system,[J].Journal of Mechanical Engineering,2014,50(11):23-36.

[13]ABBOUDI K,WALHA L,DRISS Y,et al.Dynamic behavior of atwo-stage gear train used in a fixed-speed wind turbine[J].Mechanism & Machine Theory,2011,46(12):1888-1900.

[14]肖正明,秦大同,尹志宏.多级行星齿轮系统耦合动力学分析与试验研究[J].机械工程学报,2012,48(23):51-58.

XIAO Zhengming,QIN Datong,YIN Zhihong.Multi-stage planetary gears dynamic coupling analysis and experimental investigation[J].Journal of Mechanical Engineering,2012,48(23):51-58.

[15]SHI W,PARK H,NA S,et al.Dynamic analysis of three-dimensional drivetrain system of wind turbine[J].International Journal of Precision Engineering & Manufacturing,2014,15(7):1351-1357.

Dynamic characteristics of a wind turbine drive train with flexible supports

ZHANG Shenglin,ZHU Caichao,SONG Chaosheng,HUANG Huaqing

(The State Key Laboratory of Mechanical Transmission，Chongqing university，Chongqing 400030,China)

In order to acquire wind energy in high sky,most of wind turbines are installed on 100-meter high towers.The flexibility of tower makes force,stress and deformation of wind turbine drive train become complex,and the wind turbines are always under direction-varying wind loads and harsh working conditions.So,the drive train becomes a weak link.A three-point supported wind turbine model installed on a flexible tower was analyzed,and the 3 supports’ parameters were extracted with the finite elements method,then the dynamic coupled model of the drive train with flexible supports was established.The natural characteristics of the model were studied.The first two order natural frequencies of the system respectively corresponded to the tower’s swing and the drive train’s torsional vibration.Campbell diagram was used to get the potential resonance frequencies of the drive train.The modal-energy was calculated.To identify the potential resonance points and it was shown that 1.55 Hz is the potential resonance frequency of the drive train.Tests were conducted in the wind field,the vibration characteristics of the wind turbine main shaft were monitored with variation of rotating speed.The results showed that the tested resonance frequency of the drive train is 1.56 Hz,compared with the calculated one the error is one percent.

wind turbine; drive train; dynamic behavior; flexible supporting; coupling analysis

国家科技支撑计划资助(2012BAA01B05);中央高校基本科研业务费专项(106112015CDJXY110008)

2015-05-20修改稿收到日期：2015-09-16

张盛林 男，硕士生，1989年1月生

朱才朝 男，博士后，教授,博士生导师，1966年8月

TH132.413

A DOI:10.13465/j.cnki.jvs.2016.17.008