仿人机器人运动数据计算与分析

郭瑞君 辛洪兵 张帆 邓曼

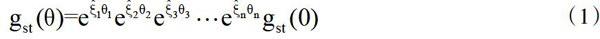
摘  要：仿人机器人动作设计所需的运动数据的获取，多数采用通过视频采集运动捕捉系统获取人体运动的数据，将所得数据与仿人机器人简化模型进行定向匹配，利用旋量理论中逆运动学计算求解，得到仿人机器人简化模型的关节转角运动数据，为仿人机器人仿真分析和控制提供参数。

关键词：仿人机器人;简化模型;旋量理论;逆运动学

引言

仿人机器人的运动规划是依据人类活动而进行的。因此，研究人体运动姿态可以为仿人机器人运动规划提供依据。现在常用的人体步态数据获取方法有基于视频和图像的采集方法和采集物理信号的采集方法。基于视频和图像的采集方法主要是通过多摄像机来标定身体上预先设置好的点的位置，或者是通过工作空间多个2维图像来确定位置[1-2]。通过该方法获得的标记点的空间坐标参数，需要通过计算与分析，才能获得与仿人机器人进行运动匹配的关节数据[3]。

1 建立仿人机器人简化模型

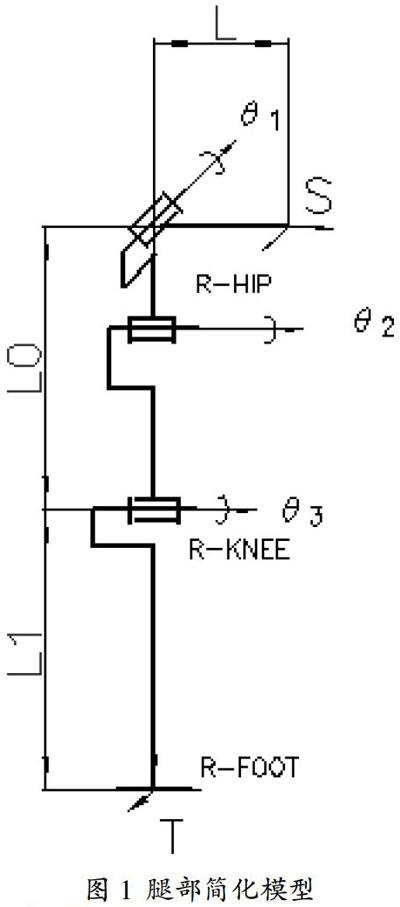
文章选取仿人机器人腿部结构进行计算和分析，根据仿人机器人的结构特点，建立仿人机器人腿部简化模型，如图1所示。并建立局部坐标系T和空间坐标系S。

图1 腿部简化模型

2 仿人机器人腿部关节角度计算

通过视频采集运动捕捉系统采集的腿部标记点的数据，结合旋量理论中逆运动学方法，可以求解出腿部各关节的角度信息。

在不考虑仿人机器人的踝关节运动情况下，仿人机器人的每一条腿有3个自由度，分别是髋关节左右转动θ1角度和前后转动角度θ2，膝关节前后转动角度θ3。实验过程中，选取人体髋关节点q1、膝关节点q2和踝关节点q3处作为标记点，通过动作捕捉系统获取标记点的空间坐标。

根据旋量理论中正运动学方法知，

机器人运动学正解映射gst：Q→SE（3）有以下形式：

式中：gst（θ）-当关节矢量θ=（θ1，θ2，…，θn）已知时，此时坐标系T相对于坐标系S的相对位姿;gst（0）-当机器人处于参考位形时，坐

标系T相对于坐标系S之间的相对位姿[4]。

运动旋量公式：

运动旋量指数函数变换公式：

（3）

根据图1所示的腿部简化模型，选取腿部直立姿态为参考位形，得到坐标系T相对于坐标系S的相对位姿：gst（0），选取腿部标记点q1、q2、q3，髋关节和膝关节三个转动轴的矢量：ω1、ω2、ω3。根据运动旋量公式可求得三個转动关节对应的运动旋量为：ξ1、ξ2、ξ3。根据运动旋量指数函数变换公式可得：e，e，e。

根据视频采集动作捕捉系统所得的人体数据，可以得到坐标系T相对于参考系S的期望位形gd=gst（θ），将上述公式带入公式（1），利用Paden-Kahan子问题可以求解出腿部各关节的转角θ1、θ2、θ3，具体推导过程不再详细介绍。

3 结束语

文章通过对仿人机器人运动规划所需的关节角度数据的获取方法进行阐述，详细介绍旋量理论中逆运动学在仿人机器人运动数据的获取中的应用，为仿人机器人的运动数据获取提供参考。

参考文献

[1]Eberhart HDA. Fundamental Studies of Human Locomotionand other Information Relating to Design of Artificial Limbs[D]. Berkeley： University of California， Berkeley，1947.

[2]Inman VT， Ralston HJ， Todd F. Human Walking[M]. Baltimore： Williams &Wilkins，1981.

[3]张利格，毕树生，高金磊.仿人机器人复杂动作设计中人体运动数据提取及分析方法[J].自动化学报，2010（1）.

[4]（美）理查德·摩雷（RichardM.Murray），等.机器人操作的数学导论[M].徐卫良，钱瑞明，译.机械工业出版社，1998.