几何直观在计算教学中的一点思考

孟凌飞

《义务教育数学课程标准（2011年版）》新增了几何直观这个核心词汇，也是课标的十个核心概念之一，可见，几何直观在数学教学中的地位与作用。几何直观不仅在图形与几何中用到，在数的运算教学中能用直观的办法、用图形的办法，把它描述刻画出来，会使这个对象更容易理解。在计算教学中，算理是算法的理论依据，算法是算理的提炼和概括，它们是相辅相成的，学生计算能力的提高，不仅是计算熟练程度的提高，更是学生对计算算理的理解。西藏的整体教育水平比我们要低很多，整体的计算能力和数感也很差，因此，运用几何直观帮助学生理解算理，掌握算法提高学生的数学素养，也更加迫切。

一、实物直观 简约算理

小学生，尤其是小学低段的学生对生动、形象、具体的事物易记住，而对枯燥、单一、乏味、抽象的数学知识毫无兴趣。因此在许多的公开课、展示课的教学中许多教师不愿意选择计算类型的课题，在一些常态课中教师也往往是出示例题后，直接告诉孩子们算理，然后通过反复练习来让孩子理解，其结果好多孩子计算常常犯错。而几何直观能够将其枯燥的数学知识直观化、形象化、趣味化，让学生感受到所学的知识是，可观察的，可触摸的，具有现实存在感。实物直观可以是我们生活中实际存在的物体，也可以借助小棒、圆形、卡片等辅助的实物教具、学具。低年级学生以具体形象思维为主要形式，因此，在教学时可以用实物直观，通过教师演示，学生操作来感知从而理解算理。

如：二年级的孟雪明老师在教学《100以内的进位加减法》时，运用几何直观，帮助学生理解“凑十”法的算理，从而提学生的计算能力。例4：35+37

让学生同桌合作在面摆小棒学具，先摆： + =

然后摆 + 学生通过观察，动手“拿”，使得 变成 “凑”成10个小棒，外面还有2个，“合”起來就是12个小棒。

最后将两次操作结果合并即得到72，整个计算过程，在“拿”的基础上提升，把7分成5和2，5和5凑成10，10加2是12。最后学生用语言来描述“拿、凑、合”的过程。此时，学生能很好的理解“凑十”的含义，从而掌握“凑十法”。学了35+37，举一反三。100以内退位减法，“破十法”、“连减法”也是如此。用实物直观演示，尤其是学生借助小棒的操作演示，把复杂的凑十、破十、连减变得直观、简单。

二、符号直观 深化算理

小学三、四年级的学生知觉、观察和想象趋于完善，有意想象的成分大量增加，具有直观性和具体性，小学三、四年级的学生在理解算理时，可发挥简约符号直观的价值，让算理深化提升，培养学生的数感。

如：李丽萍老师在教学《两位数乘两位数（不进位）》时采用了几何直观的符号直观，帮助学生理解积写在哪位和竖式的定法的算理。

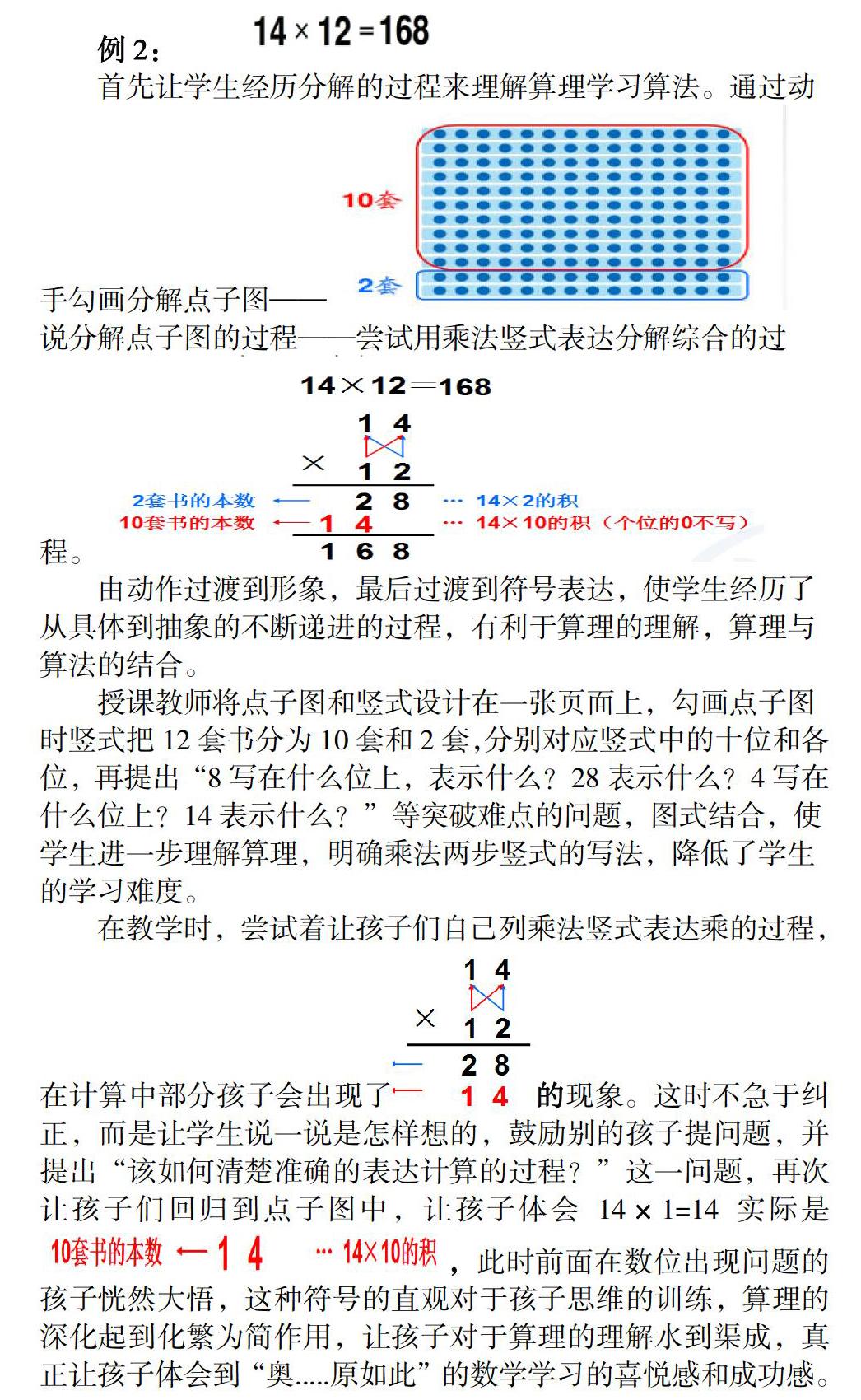
例2：

首先让学生经历分解的过程来理解算理学习算法。通过动手勾画分解点子图—— 说分解点子图的过程——尝试用乘法竖式表达分解综合的过程。

由动作过渡到形象，最后过渡到符号表达，使学生经历了从具体到抽象的不断递进的过程，有利于算理的理解，算理与算法的结合。

授课教师将点子图和竖式设计在一张页面上，勾画点子图时竖式把12套书分为10套和2套，分别对应竖式中的十位和各位，再提出“8写在什么位上，表示什么？28表示什么？4写在什么位上？14表示什么？”等突破难点的问题，图式结合，使学生进一步理解算理，明确乘法两步竖式的写法，降低了学生的学习难度。

在教学时，尝试着让孩子们自己列乘法竖式表达乘的过程，在计算中部分孩子会出现了 的现象。这时不急于纠正，而是让学生说一说是怎样想的，鼓励别的孩子提问题，并提出“该如何清楚准确的表达计算的过程？”这一问题，再次让孩子们回归到点子图中，让孩子体会14×1=14实际是 ，此时前面在数位出现问题的孩子恍然大悟，这种符号的直观对于孩子思维的训练，算理的深化起到化繁为简作用，让孩子对于算理的理解水到渠成，真正让孩子体会到“奥.....原如此”的数学学习的喜悦感和成功感。

借助于几何直观、几何解释，能启迪思路，可以帮助学生理解和接受抽象的内容和方法，揭示研究对象的性质和关系，使思维很容易转向更高级更抽象的空间形式，使学生体验数学创造性工作历程，能够开发学生的创造激情，形成良好的思维品质。用图形说话，用图形描述问题，用图形讨论问题，应当成为学生的一种基本的数学素质。

数与形，本是相倚依，焉能分作两边飞；

数无形时少直觉，形少数时难入微；

数形结合百般好，隔离分家万事休；

切莫忘，几何代数流一体，永远联系莫分离。 -----华罗庚