劳动力错配对中国工业行业出口净技术复杂度的影响

陈乐一　黄青青　杨　云

(湖南大学，湖南　长沙　410079)



劳动力错配对中国工业行业出口净技术复杂度的影响

陈乐一黄青青杨云

(湖南大学，湖南长沙410079)

要素市场发育不良、市场化进程落后导致要素过度拥挤和无效配置，严重制约了我国工业行业出口净技术复杂度的持续升级。基于1999-2013年SITC三位码产品层面的进出口数据，笔者测算出了中国32个工业行业的出口净技术复杂度，并对劳动力错配与行业出口净技术复杂度之间的关系进行分析。回归结果显示，劳动力错配与出口净技术复杂度之间呈现倒“U”型关系，即劳动力错配程度较低时，劳动力错配与出口净技术复杂度存在正向关系，当劳动力错配超过某一临界值时，劳动力错配抑制出口净技术复杂度的提升。进一步研究发现，劳动力错配对出口净技术复杂度的影响效果存在行业差异性，资本技术密集型行业和国有企业比重相对较高的行业，降低劳动力错配程度对出口净技术复杂度的促进效应较大。

劳动力错配；出口净技术复杂度；中国工业行业；倒“U”型

一、引言

随着经济开放度的提升，中国经济实现了稳步增长。出口导向型贸易战略的实施使我国的对外贸易发展也取得了显著的成绩，其中出口贸易额从1990年的620.9亿美元迅速上升到2013年的22090.0亿美元，实现了17.63%的年均增长率，远超过世界同期的增长速度。我国出口贸易量迅速增加的同时，出口产品的技术含量也发生了明显的变化，产品逐渐由技术含量低的劳动资源密集型过渡到高技术含量的资本密集型。近几十年来我国出口复杂度得到一定提升，但在世界范围内，还处在较低水平，而这已经制约了中国经济的进一步增长。出口复杂度的提升受限，可能不仅仅是因为缺少诸如人力资本、技术、自然资源或创新等资源，还可能是由于错误配置或错误使用资源导致的。

从整个经济系统来看，出口复杂度受到各个因素的影响。从经济系统外部因素来看，国内外研究多从经济增长、加工贸易、FDI等几个视角来研究出口复杂度的影响机制。[1][2][3]另外，从内部因素来看，现有研究多从金融发展、基础设施、人力资本、市场化进程、生产率等来解释出口复杂度的变迁过程。[4][5]

要素配置效率是影响一国经济增长质量的关键因素，也是全要素生产率和产出效率增长的主要来源，国外学者已经开始关注要素错配的形成过程及其对经济产出效率的影响。持续快速的经济增长是中国工业行业出口复杂度稳步提升的主要动力，[1]而劳动力错配却不断地削弱经济增长的潜力和动力。我国经济运行中的劳动力错配问题已经被学术界反复证实，对生产率水平产生了显著的负影响。如果我国的劳动力资源得到有效配置，制造业产出效率可以提高86.6%～115%；[6]要素市场扭曲往往伴随着要素流动受限，从而未能实现要素的最优配置，最终给社会带来极大的效率损失；[7]由于工业行业要素错配导致的产出缺口达到29%，分行业来看，劳动配置效应比较大的行业主要是技术密集型行业和劳动密集型行业。[8]同时，也有部分学者发现，要素价格扭曲在短期内提升了我国企业出口的多元化水平，[9]劳动力价格扭曲的加剧能有效地推动中国工业企业出口复杂度的升级。[10][11]

在发展中国家，要素的无效配置现象更为普遍，因此可以在不增加要素投入的前提下，通过减少要素错配，使经济产出水平和生产效率得到大幅提高。我国无法在短时期内通过大规模引进技术提升生产效率，也无法迅速提升要素质量以及技术水平。因此，通过消除要素流动障碍，提高存量要素配置效率来提高生产效率，从而提升出口净技术复杂度水平，才是实现经济可持续发展的战略选择。接下来，笔者在合理选择劳动力错配以及出口复杂度的衡量指标的基础上，分析中国工业行业的劳动力错配与出口复杂度的关系，并从总体和行业分组两个层面上检验劳动力错配对工业行业出口复杂度的影响，最终根据所得结论，提出促进中国工业行业劳动力资源的优化配置以及出口复杂度可持续提升的政策建议。

二、理论分析与相关假设

劳动力错配是指劳动要素投入由于流动障碍和制度约束等，自由配置受到阻碍，导致要素过度分配或配置不足的现象。中国劳动力配置扭曲，究其根源主要在于劳动力市场的行业和内部分割以及工资决定机制非市场化，劳动力价格偏离劳动边际生产力所确定的均衡工资，往往被低估或高估，劳动力资源未得到优化配置。基于已有的经济学理论以及上述关于劳动力错配与出口复杂度的文献回顾，本文认为劳动力错配会对工业行业出口复杂度产生如下的影响。

从生产效率角度来分析，已有大量的实证研究证明提高存量劳动力要素的配置效率对产出以及全要素生产率的提高具有巨大的潜力，我国经济的潜在增长率水平也能得到明显的提高。[6]从企业的角度来看，要素市场扭曲使企业将有限的资源用于寻租等非生产性活动，对企业进行生产设备更新、新工艺的采用以及员工技能培训等实体投资产生了挤出效应，使生产效率停滞不前，从而有碍于出口复杂度的提高。当劳动市场实行管制，即劳动市场扭曲时，一些优秀的企业由于受到投入品配额的限制无法进行规模扩张，从而丧失了通过规模效应带来的生产效率提高的机会，此外，为了生产计划内投入品，一些经营不善的低效率企业却被保留下来，使市场整体生产率的提高受到极大的限制。从劳动者的角度来看，劳动者所得低于其所创造的价值，即人力资本未得到合理的回报，严重打击了劳动者的生产积极性，这必然也会影响企业的生产效率。

劳动力错配会阻碍技术进步，从而对出口复杂度产生负面的影响。生产要素的价格扭曲和被压低的现状会对要素所有者产生错误的激励，不利于人力资本积累和技术创新。一方面，过低的收入会挫伤劳动者对自身或者后代教育进行投资的积极性，不利于人力资本的形成和积累，对技术创新产生负面的影响；另一方面，若得到的报酬与劳动付出不成正比，优秀人才的流失将使企业丧失更多的研发资源，进而导致与吸收流失人才企业的技术差距进一步扩大，对其技术创新产生负面的影响。根据新古典经济理论，当企业产生劳动工资上涨的预期时，将更偏好于采用先进的资本而不是简单的劳动，企业劳动生产率因此得以提高。[12]同理，工资下跌将会促使企业更倾向于依赖廉价要素的使用来获取利润，丧失了技术研发的动力。由于企业在进行经济决策时是以利润最大化为目标，因此在生产要素的价格被大幅低估的情况下，企业将更倾向于投入物质资本而不是开展技术创新活动。劳工成本高，技术创新的机会成本低。若劳工成本下降，技术创新的机会成本上升，企业将使用更多的劳工，而减少对技术与资本的使用，最后表现出来的是出口技术复杂度降低。另外，劳动力收入偏低导致消费者的需求层次偏低，缺乏对高端产品的市场需求，企业研发缺乏动力，从而对企业的技术创新活动产生负向的抑制作用。而由于要素市场扭曲而盛行的寻租活动，也将使企业自主研发面临更大的不确定性以及风险，进而对技术创新产生更显著的负向抑制作用。[13]由此，本文提出以下假设：

H1：劳动力错配通过引致生产效率损失，阻碍经济增长的正向效应以及抑制技术创新，阻碍技术进步，对我国工业行业出口复杂度的提升产生了负向的抑制作用。

从企业的角度来看，当劳动力价格被低估时，一方面，企业部分劳工成本得到节约，因此更多的资金能够被用于新产品的技术研发，改进了的产品生产工艺使企业整体竞争力增强，对出口技术复杂度产生正向的促进作用，同时劳工成本的节约使企业的利润增加，分配到产品研发部门的利润也会随之增加，最终使得专利费增加，这使得产品研发部门的利润空间更大，因此，将会有更多的厂商选择进入产品研发部门，从而促进整个行业产品技术含量的提高，此外，劳工成本下降意味着产品的生产成本将低于国际的价格水平，因此出口产品尤其是劳动密集型产品在国际市场上具有较强的价格竞争优势；另一方面，在产品价格由市场机制决定的情况下，劳动力价格被低估使得企业能够实现超额利润，财富集中在企业所有者手中，导致储蓄过多，实际利率下降，资本的真实价格降低，促使企业加大投资力度，因而企业在技术研发方面更容易获得资金支持。当劳动力价格被高估时，短期内，劳工成本增加使企业丧失部分利润，但长期内，过高的劳工成本将引致技术对劳动的替代，企业将引进先进的生产技术和设备替代部分劳动，最终生产出更高质量的产品，从而促进出口复杂度的提升。劳动力价格被高估，企业的劳工成本上升，将使研发企业减少劳动力的雇佣数量，但同时生产部门的劳动力雇佣量也受到挤压，劳动力向研发部门转移，壮大了研发企业的队伍，从而提高了产品质量升级的概率。此外，要素价格扭曲在短期内提升了我国企业出口的多元化水平，[9]增强了企业的国际竞争力。从劳动者的角度来看，劳工成本上升意味着劳动力收入水平上升，消费结构高级化，而高端产品的生产需要更高的技术创新能力与之匹配，因此企业将采用更先进的技术和生产工艺以满足高端产品需求的出现，这必然会引起出口复杂度的上升。由此，本文提出以下假设：

H2：引致劳动力错配的劳动力价格扭曲通过节约生产成本，促进研发投入，增加企业出口产品的多元化水平以及引致技术对劳动的替代等方式对我国工业行业出口复杂度的提升产生了正向的促进作用。

虽然劳动力价格扭曲能促进出口复杂度的提升，即当劳动力价格被低估时，企业可以节约生产成本，使本土产品在国际市场上具有较强的价格竞争优势，同时厂商也可将节约的资源投入到产品的研发活动中；当劳动力价格被高估时，由于劳工成本的持续上涨，将引致技术对劳动的替代，此外，劳动力收入水平上升，消费需求的高级化将促使企业采用新技术和新工艺，使生产结构进一步优化，但是当劳动力错配程度超过某一临界值时，可能导致大量的生产效率损失，并对技术进步产生严重的阻碍作用，此时，劳动力错配对出口复杂度的抑制效应大于促进效应，表现为负的净效应。由此，本文提出以下假设：

H3：劳动力错配与出口复杂度之间存在倒“U”型关系，即劳动力错配程度较低时，劳动力错配与出口复杂度存在正向关系，当劳动力错配超过某一临界值时，劳动力错配抑制出口复杂度的提升。

三、计量模型、变量与数据

(一)计量模型

为了从实证角度检验劳动力错配和工业行业出口净技术复杂度之间的关系，我们构建一个基于行业层面的出口净技术复杂度影响因素的模型，基本形式如下：

(1)

其中，i代表行业，t代表年份，k表示控制变量的个数，LnNTSIit表示行业出口净技术复杂度对数值，我们借鉴杜传忠和张丽[14]的方法，测算了基于国际垂直专业化分工视角的出口品国内技术复杂度指数，也称出口净技术复杂度指数，MISit表示i行业的劳动力错配系数。α0为常数项，εit表示随机扰动项，Xjit是一组控制变量，具体包括企业数目对数值(LnNUM)、国有企业比重(MON)、人均资本对数值(LnRCAPL)、进口贸易变量(IMP)、人力资本对数值(LnH)、外商直接投资(FDI)、研发投入对数值(RD)，vi表示个体效应。

(二)出口净技术复杂度测算及其他变量说明

1.出口净技术复杂度的测算

为计算行业的出口净技术复杂度，首先借鉴Rodrik[1]的方法，将产品j的出口技术复杂度(PRODYj)定义为：

(2)

其中，k，c表示国家或者地区，xj,k为k国j商品的出口额，∑jxj,k，∑jxj,c表示国家的总出口额，Yk为k国经购买力平价后的人均GDP。然后利用国民经济行业分类标准(GB)与国际贸易标准分类(SITC)的对照表，[15]以各行业出口额中每种产品出口额所占的比重为权重，计算得到行业i的出口复杂度(TSIi)如式(3)：

(3)

其中，xj,i表示i行业j商品的出口额。然而，利用以上方法测算的行业出口技术复杂度，未考虑加工贸易的影响，无法反应一国真实的出口技术复杂度。现有文献[16]通过严格的数学证明得出一国各部门的完全国内增加值系数与完全进口额系数之和等于1：

BV+BM=u

(4)

其中：BV代表各部门完全国内增加值系数行向量；BM代表各部门完全进口额系数行向量，也为Hummels et al.[17]提出的垂直专门化率。因此，完全国内增加值系数等于1减去各部门的垂直专门化率。为了剔除出口商品中所包含的进口中间投入品价值，我们借鉴杜传忠和张丽[14]的做法。将以上定义的商品出口复杂度(PRODYj)以及行业出口复杂度(TSIi)修正得到商品的出口净技术复杂度(NPRODYj)和行业的出口净技术复杂度(NTSIi)：

(5)

(6)

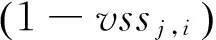
在测算产品和行业的出口净技术复杂度的过程中，本文采用1999-2013年按国际标准SITC Rev.3的三位数分类的进出口产品数据，它们来自联合国贸易发展委员会(UNCTAD)的国际贸易分类统计数据库，其中各国人均GDP数据来源于世界银行的WDI数据库，同时为了使计算结果在时间上具有可比性，各国人均GDP均采用以2000年为基期且按购买力平价(PPP)衡量的不变价。

2.劳动力错配的测度

假设经济中有n个行业，每一个行业i的生产函数为：

Yi=AiKiαiLiβi

(7)

其中，Ki、Li分别表示资本和劳动力生产要素，αi、βi则分别表示各生产要素的产出弹性。根据厂商利润最大化的原理，一阶条件可以表示为：

(8)

(9)

本文借鉴韩国珍[8]的做法，将行业i的劳动力配置扭曲系数定义为：

(10)

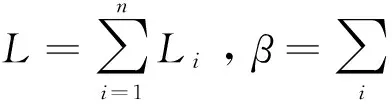
为了统一度量劳动力错配程度，本文借鉴韩国珍(2015)[8]的思路，用下式来定义行业i的劳动力错配，采用劳动力配置扭曲系数与1的偏离程度来度量。

(11)

3.其他控制变量

按照以往研究的经验[4][19]，选取的控制变量主要包括以下指标：

国有企业比重(MON)采用国有企业总产值占行业总产值份额来表示；人均资本(RCAPL)采用各行业人均固定资产净值年平均余额表示；进口贸易变量(IMP)采用各行业的进口额除以该行业工业增加值表示；人力资本(H)以各行业科技研发人员表示；外商直接投资(FDI)采用各行业三资企业的固定资产净值占该行业固定资产净值年平均余额比重来表示；研发投入(RD)以各行业人均科研人员科技活动经费内部支出来表示；此外，控制变量还包括行业内企业数目对数值(LnNUM)。

由于数据的可得性，本文选取1999-2013年中国工业行业的数据，其中规模以上工业行业企业数目、国有企业总产值、工业总产值、全部从业人员年平均人数、主营业务收入等数据均来自各年度《中国工业经济统计年鉴》；各行业科技活动经费内部支出、科技研发人员来自相应年份《中国科技统计年鉴》；为了消除价格因素的影响，所有货币单位数据均折算成2000年不变价。

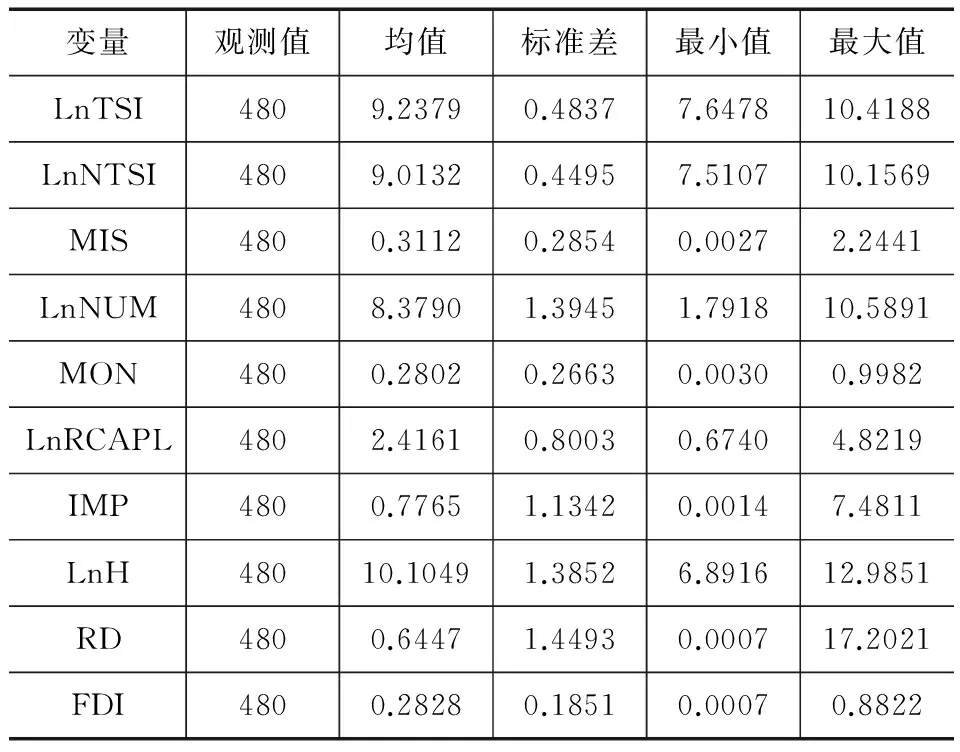
表1　主要指标统计性描述(1999-2013)

四、实证结果分析

在验证劳动力错配对出口净技术复杂度的影响时，对于是否存在个体效应，我们用固定效应模型和随机效应模型进行估计并用Hausman统计量检验是否存在个体效应。

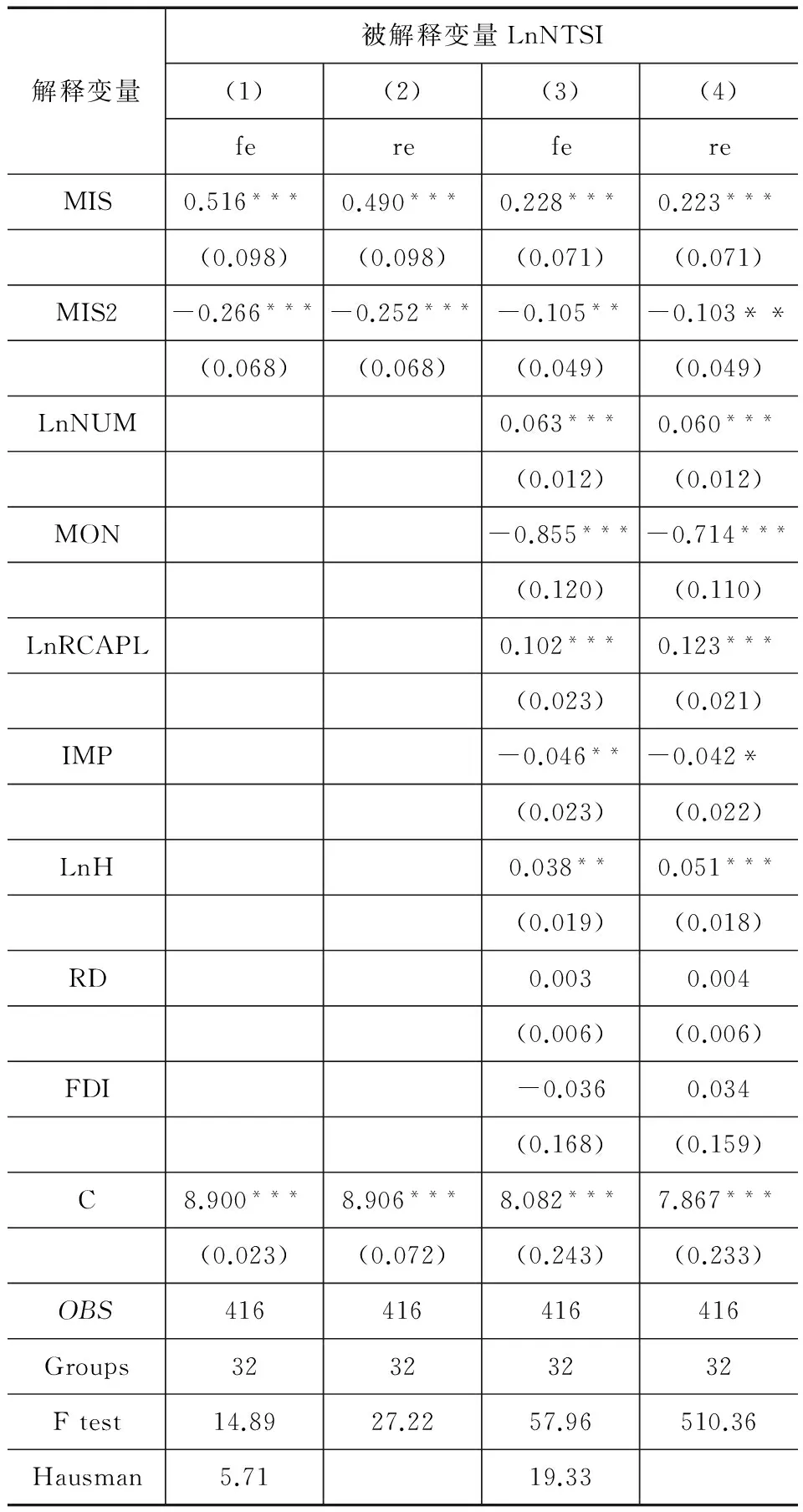
表2　劳动力错配影响出口净技术

注: 本文使用 stata12.0计算，FE表示固定效应模型; RE表示随机效应模型;***、**、*分别表示在1%、5%、10%的水平上显著，括号内为标准差。

从表2可以看出Hausman统计量的P值为0.000，强烈拒绝原假设，所以应该采用固定效应模型，而不是随机效应模型。结果显示，劳动力错配系数始终在1%的显著性水平下显著为正，劳动力错配平方项系数始终为负，并且都统计显著，这说明劳动力错配与出口净技术复杂度之间存在稳定的倒“U”型关系。

具体来看，方程(1)和方程(2)的解释变量只有劳动力错配及其平方项，劳动力错配及其平方项系数分别为0.516、-0.266，均通过了显著性检验。加入各控制变量之后，劳动力错配及其平方项系数分别为0.228、-0.105，其符号及显著性均未发生根本性变化，证实了总体估计结果中劳动力错配与出口净技术复杂度倒“U”型关系的稳健性。这表明我国的劳动力错配在一定程度上对出口净技术复杂度的提升产生了促进作用，但随着劳动市场环境的恶化，加剧了劳动力资源配置的扭曲程度，劳动力错配从正向的助推力转为负向抑制作用。这是因为在早期，我国的要素市场化改革相对滞后，劳动力价格往往被低估，因此企业能够以更低的价格获得高质量的生产要素，在降低生产成本的同时也在一定程度上缓解了企业面临的预算约束问题，使部分资金可以转向投入到产品先进生产技术的研发，从而使出口净技术复杂度得到提升。但从长期来看，随着地方政府对市场价格以及资源配置的干预，损害了资源配置效率和劳动力的市场定价机制，加剧了我国劳动力市场扭曲，使寻租行为愈加盛行，部分生产者丧失了提升生产过程中技术水平的动力，使出口净技术复杂度提升受阻。

至于其他控制变量，行业内的企业数目(LnNUM)、人均资本(LnRCAPL)、人力资本(LnH)均对出口净技术复杂度具有显著稳健的促进作用，这与已有的研究结论保持一致；外商直接投资(FDI)的估计系数为正，但不具有统计显著性，一方面可能是由于我国企业的学习接受能力存在不足，技术差别仍较大，阻碍了外资流入所带来的正向技术溢出效应的发挥。另一方面，政府对部分企业的过度保护不利于企业面对来自跨国公司的竞争压力，影响了本土企业对新技术的吸收和创新，使其丧失了改进技术、工艺和提高自主开发能力的动力，从而造成了外资进入对我国出口净技术复杂度深化的促进作用并不明显；研发投入(RD)回归系数为正，但不具有统计显著性意义，这可能是由于我国当前工业行业企业的研发投入强度不足，研发资金使用效率过低，造成研发能力过低，因此，研发强度的增加并没有使出口净技术复杂度得到提升；进口贸易变量(IMP)的估计系数为负，在10%显著性水平通过变量显著性检验，即对出口净技术复杂度的抑制效应显著，部分印证了我国加工贸易在全球价值链中被低端锁定的观点；国有企业比重(MON)的回归系数显著为负，这可能是因为：(1)国有企业的技术效率相对低下，并且对生产要素具有优先配置的权利，要素市场扭曲加剧，从而抑制了出口净技术复杂度的提升；(2)国有企业面临着预算软约束与委托代理问题，这造成了国有企业的生产效率和创新效率的双重损失。[20]

考虑到我国工业行业间存在较大的差异，劳动力错配对出口净技术复杂度的作用机制可能不尽相同。一方面，我们按照要素密集度将工业行业总体划分为劳动密集型行业与资本技术密集型行业，并分别进行回归，具体见表3的(1)-(2)列。另一方面，根据中位数原则，进一步按国有企业比重划分为国有企业比重较高的子样本和较低的子样本，分析在不同的国有企业比重下劳动力错配对出口净技术复杂度的影响，具体见表3的(3)-(4)列。

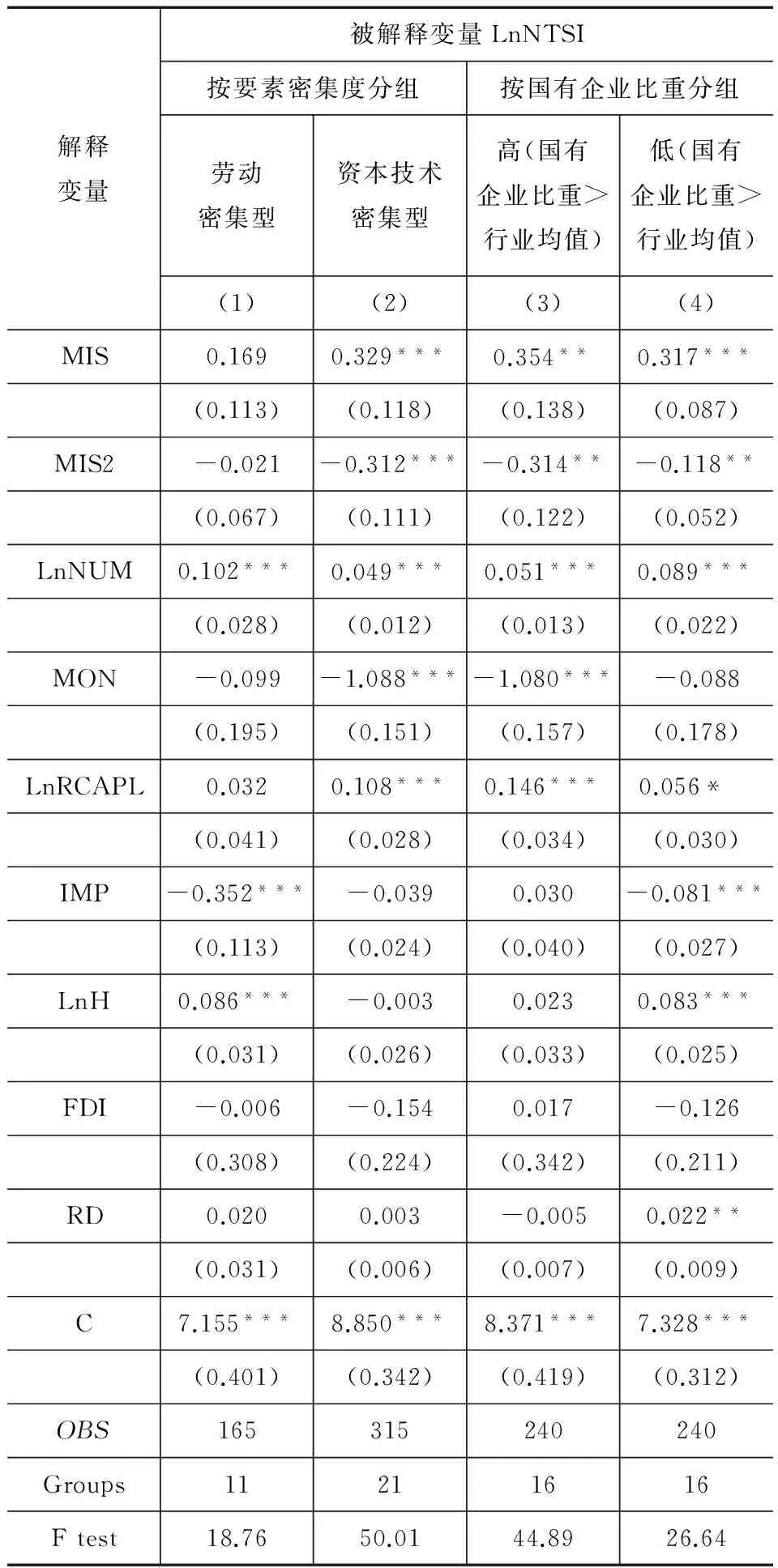
表3　按要素密集度和国有企业比重分组的估计结果

注:***、**、*分别表示在1%、5%、10%的水平上显著，括号内为标准差。

按要素密集度划分的结果表明，对于劳动密集型行业，劳动力错配对出口净技术复杂度产生的倒“U”型影响并不明显；对于资本技术密集型行业，劳动力错配及其平方项系数分别为0.329、-0.312，均通过了显著性检验。通过比较两个子样本的估计系数，可以发现不同要素密集度行业劳动力错配对出口净技术复杂度的影响确实存在差异，相对于劳动密集型行业来说，资本技术密集型行业的劳动力价格扭曲对出口净技术复杂度的抑制作用较大，这可能是因为：一方面，与劳动密集型行业相比，资本技术密集型行业的技术含量相对较高，因而劳动力错配通过阻碍技术进步对资本技术密集型行业出口净技术复杂度产生的抑制作用更大；另一方面，相对于劳动密集型行业来说，资本技术密集型行业的劳动力错配导致的生产效率损失更大，[21]因此劳动力错配通过导致生产效率损失对资本技术密集型行业出口净技术复杂度产生的抑制作用更大。

按国有企业比重划分的结果表明，当国有企业比重较高时，劳动力错配及其平方项系数分别为0.354、-0.314，均通过了5%的显著性水平检验；国有企业比重较低时，劳动力错配及其平方项系数分别为0.317、-0.118，均在5%的水平上显著，表明劳动力错配对出口净技术复杂度均存在倒“U”型影响。结合劳动力错配及其平方项的系数可知，相对于国有企业比重较低的行业，国有企业比重较高的行业具有较低的门槛值，此外，通过比较劳动力错配平方项的系数大小，可以发现当国有企业比重较高，行业的垄断程度越大时，劳动力错配的抑制效应更加显著，这表明国有企业比重较高与较低行业劳动力错配对出口净技术复杂度的影响确实存在差异。这可能是因为国有企业在国内市场上的垄断地位，具有获得廉价要素的优先权，使得劳动力价格被低估对其出口净技术复杂度提升的作用力不显著，此外国有企业较低的行业的经营效率以及技术敏感性，也在一定程度上降低了劳动力价格扭曲对其出口净技术复杂度促进作用的发挥[22]，同时较高的国有企业比重将加剧劳动力市场的扭曲，因此对出口净技术复杂度的抑制作用更大。

五、结论与政策启示

本文从促进效应和抑制效应两个角度分析了劳动力错配影响出口净技术复杂度的内在机理，基于SITC Rev.3的三位数分类的进出口产品数据，计算了我国工业行业1999-2013年的出口净技术复杂度，并检验了劳动力错配对出口净技术复杂度的影响，其主要结论概括如下：第一，劳动力错配对出口净技术复杂度的影响包括两个方面：促进效应和抑制效应；第二，总体来看，劳动力错配对中国工业行业出口净技术复杂度的作用呈现倒“U”型关系，即在劳动力错配水平较低的阶段，劳动力错配程度的提高将促进出口净技术复杂度提升，但当劳动力错配达到一定水平后，劳动力错配状况的恶化将阻碍出口净技术复杂度的提升；第三，在按要素密集度以及国有企业比重分组的子样本实证分析中，资本技术密集型行业的劳动力错配与出口净技术复杂度的倒“U”型关系较为显著，劳动密集型行业则不明显。无论是国有企业比重较高的行业还是比重较低的行业，劳动力错配与出口净技术复杂度均表现为倒“U”型关系。

基于以上分析，本文提出政策建议如下：首先，由于目前我国工业行业劳动力市场的扭曲以及非有效配置的现象还普遍存在，为了有效改变这一现状，要加快要素市场的市场化进程，使要素价格正确反映资源的稀缺性和机会成本，发挥市场在劳动力配置中的决定性作用，提高劳动力资源的利用效率，实现出口净技术复杂度的可持续升级；其次，政府需充分考虑行业的差异性，并制定政策和措施激励企业的技术创新行为，从而促进出口净技术复杂度的提升；最后，破除制约劳动力优化配置的壁垒，促进劳动力的自由流动，提高劳动力要素的再配置效应。

[1] Rodrik，D..What's So Special about China's Exports?[J].China&world Economy, 2006,14(5):1—19.

[2] Wang Z，Wei S.What Accounts for the Rising Sophistication of China's Exports?[J]. NBER Chapters, 2010: 63-104.

[3] Xu B，Lu J.Y.Foreign direct investment, processing trade, and the sophistication of China's exports[J].General Information, 2009(20):425-439.

[4] 王永进，盛丹，施炳展，李坤望.基础设施如何提升了出口技术复杂度?[J].经济研究，2010(7):103—115.

[5] 刘洪铎，吴庆源，李文宇.市场化转型与出口技术复杂度:基于区域市场一体化的研究视角[J].国际贸易问题，2013(5):32—44.

[6] Hsieh C. T.,Klenow P. Misallocation and Manufacturing TFP in China and India[J].Quarterly Journal of Economics,2009,124(4):1403—1448.

[7] Jones，C.I.,Misallocation, Economic Growth, and Input-Output Economics[R]. National Bureau of Economic Research, Inc, 2011.

[8] 韩国珍，李国璋.要素错配与中国工业增长[J].经济问题，2015(1):69—76.

[9] 耿伟.要素价格扭曲是否提升了中国企业出口多元化水平?[J].世界经济研究，2013(9):49—67.

[10] 踪家峰，杨琦.要素扭曲影响中国的出口技术复杂度了吗?[J].吉林大学社会科学学报，2013(2):106—114.

[11] 陈晓华，刘慧.要素价格扭曲、外需疲软与中国制造业技术复杂度动态演进[J].财经研究，2014(7):119—131.

[12] Kennedy，C.,Induced Bias in Innovation and the Theory of Distribution [J]. Economic Journal 1964,74(295):541—547.

[13] 张杰，周晓艳，李勇.要素市场扭曲抑制了中国企业R&D[J].经济研究，2011(8):78—91.

[14] 杜传忠，张丽.中国工业制成品出口的国内技术复杂度测算[J].中国工业经济，2013(12):52—64.

[15] 盛斌.中国对外贸易政策的政治经济分析[M].上海市：上海人民出版社，2002(11):470—471.

[16] 刘遵义，陈锡康，杨翠红.非竞争型投入占用产出模型及其应用——中美贸易顺差透视[J].中国社会科学，2007(5):91—103.

[17] Hummels, D., Ishii, J., and Yi, K.M. The Nature and Growth of Vertical Specialization in World Trade[J].Social Science Electronic Publishing, 1999, 54(1):75—96.

[18] Dean, J.M., Fung, K.C., and Wang, Z.How vertically specialized is Chinese trade?[R]. Bank of Finland, Institute for Economies in Transition, 2008.

[19] 张先锋，张敬松，张燕.劳工成本、双重创新效应与出口技术复杂度[J].国际贸易问题，2014(3):34—43.

[20] 吴延兵.国有企业双重效率损失研究[J].经济研究，2012(3):15—27.

[21] 陈永伟, 胡伟民. 价格扭曲、要素错配和效率损失:理论和应用[J]. 经济学：季刊, 2011(4):1401-1422.

[22] 刘慧，陈晓华，吴应宇.基于异质性视角的中国企业创新决策机制研究[J].中南财经政法大学学报，2013(3):143—150.

[责任编辑：唐少奕]

陈乐一，湖南大学经济与贸易学院教授、博士生导师，主要研究方向：宏观经济学；黄青青，湖南大学经济与贸易学院硕士研究生，主要研究方向：国际贸易；杨云，湖南大学经济与贸易学院博士研究生，主要研究方向：宏观经济学。

F249.2

A

1002-6924(2016)05-119-126