饱和黏性土中污染物运移一维模型试验研究

胡钦君，杨会林，张　檑

(天津市勘察院，天津 300191)



饱和黏性土中污染物运移一维模型试验研究

胡钦君，杨会林，张檑

(天津市勘察院，天津 300191)

基于一维室内模型试验，以氯化钠溶液来模拟可溶性污染物，以饱和黏性土为介质，研究了污染物在饱和黏性土中的运移规律，分析了渗透路径的增加导致穿透曲线的相关变化，提出了弥散系数的测定方法。结果表明，随着渗透路径的增加弥散系数逐渐增大，同时证明了污染物与饱和黏性土在接触时间较短的情况下，依然存在较明显的离子的吸附解吸现象。为污染物运移模型的研究及场地的污染情况预测提供参考。

可溶性污染物；饱和黏性土；弥散系数；吸附解吸

由于经济的飞速发展，工业生产规模不断扩大，工业废水未经处理合格便被排放的现象普遍存在。研究表明，我国七大水系普遍受到不同程度污染，随着地表水的污染、下渗，导致地下水污染问题日益严重[1]。根据中国地质调查局的相关研究表明，全国90%的地下水遭受了不同程度的污染，其中60%污染严重[2]。尤其以制造业为主的城市污染情况最为严重。

地下水污染具有过程缓慢、不易发现和难以治理的特点。污染范围的不断扩大，污染程度的不断加深，引起了社会各界的广泛重视，因此，近年来许多学者对污染物的运移及修复方面做了大量的研究工作。李霄等人利用室内动态土柱装置，模拟包气带岩性环境，运用弥散系数计算公式，分别计算了以亚粘土和亚砂土为主要岩性的包气带弥散系数[3]。陈亮等人通过室内一维渗流和弥散试验，研究了不同水力梯度情况下，不同污染物对不同补给距离测量点的污染情况[4]。谢焰等人将填埋场底部土体污染物浓度的实测值与一维对流弥散解析解的计算值进行了比较，并对30年后的影响深度进行了预测[5]。

本文的目的是通过一维模型试验，研究可溶性污染物在饱和黏性土中的运移规律。建立一种方便快捷的污染物运移参数的定量判定方法，为评价各种介质携带、抵抗污染物的能力，进而建立符合实际情况的迁移模型，对污染物运移规律做出预估评价等工作提供帮助。

1　试验理论

针对一维模型试验，涉及一维水动力弥散问题。对于无限长多孔介质柱体，在示踪剂瞬时注入下，弥散问题可以得到解析解。

设有一无限长均质土柱，其中原有溶液浓度C0=0，并以速度u稳定流动。在t=0时，在x=0处瞬时注入质量为m的示踪剂。取试验土柱的中心轴线为x轴，且以流速方向为正，分析随时间t变化的浓度C(x,t)的分布，该情况下的水动力弥散方程如下：

(1)

式中：C为溶液的浓度；u为溶液流速；DL为纵向弥散系数。

其解析解可以表示为：

(2)

式中：m/ω=mf表示单位横截面积上瞬时注入示踪剂的质量；ω表示砂柱横截面积。

2　室内试验

2.1试验材料及设备

1)示踪剂：本次试验示踪剂采用氯化钠溶液，其具有无毒、安全，易溶于水，化学性质稳定，且分析方法简单可靠，误差小，灵敏度高，易于微量检测等优点。

2)土样：在某工地基坑中采取常见的黏土土样，经测试土样的粒径分布如表1所示。

表1　试验土样粒径分布

3)试验设备：如图1所示，采用高100 cm，管径8 cm的有机玻璃管作为容器。两端通过法兰连接并设有进出水口，容器侧壁由上而下设有三个传感器安装口，高度分别为为7 cm、37 cm、67 cm。采用型号为FJA-10土壤盐分传感器，该传感器具有结构简单，性能稳定可靠，读数响应时间短，操作简便等优点。不仅可以用于室内试验，也可以用于野外现场直接测定土壤中水盐含量的动态变化。配合DDB-12型电阻率仪测定试验土体中离子浓度，能够满足试验精度要求。

2.2试样制备

土样经过晾晒充分风干后，采用分层填装、逐步饱和的方法制作土柱：

1)将土样缓慢的倒入容器，每次不超过5 cm，倒入过程尽量避免振捣；

2)以较小的水头差从下部渗水使土体饱和；

3)重复以上步骤至土样填装到预定高度(本次试验为90 cm)，整个试样土体达到饱和状态；

4)保持较高水头差，调整流速使其与土柱下端出水流速相当，对土体进行淋滤；

5)经过一段时间，待电阻率仪读数稳定后，做为试验初始值，方可进行试验。

2.3试验过程

试样制备完成后，使土体上部液面高度保持在5 cm并达到稳定状态，瞬时向供液瓶中倒入氯化钠溶液，并迅速搅拌均匀，得到浓度为103mg/L的溶液作为瞬时污染源，之后每隔一定时间记录传感器的读数，根据传感器标定公式，整理得到各测点的穿透曲线如图2所示。

图1　试验设备示意图

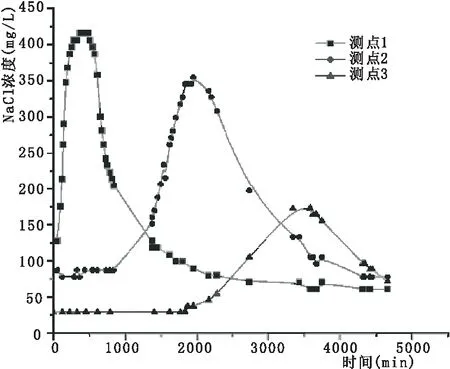
图2　各测点穿透曲线

3　结果分析

观察图2所示三条穿透曲线，可以发现：

1)各测点峰值浓度随着渗流路径的增加而不断减小，但并不呈线性递减。

2)随着渗流路径的增加，在对流-弥散作用影响下，污染晕并非均匀整体移动，而是表现出污染带加长，图上显示即为穿透曲线变宽，即同一测量浓度值在曲线上升段位置和下降段位置，时间间隔会加大。

3)根据一维水动力弥散问题理论，穿透曲线应该表现为标准的正态曲线型，但是从试验结果可以发现，曲线上，可以看出曲线峰值右侧有“拖尾”现象，线形有改变，说明在这个浓度下，盐离子在该土中出现了可以观测到的吸附-解吸过程。

由于水动力弥散方程与正态分布密度函数具有相似的形式，因此可以通过试验得到的数据进行拟合，从而计算弥散系数DL。

正态密度分布函数：

(3)

式中：x为正态变量；μ为正态变量的数学期望；σ2为正态变量的方差；σ为正态变量的标准差(均方差)。

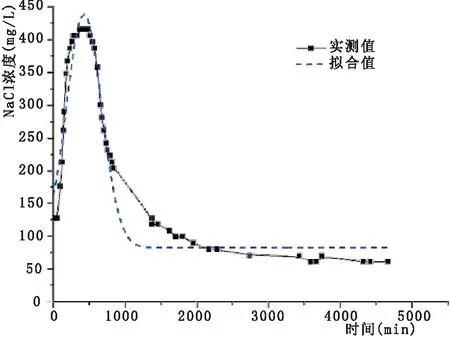
图3　测点一浓度拟合图

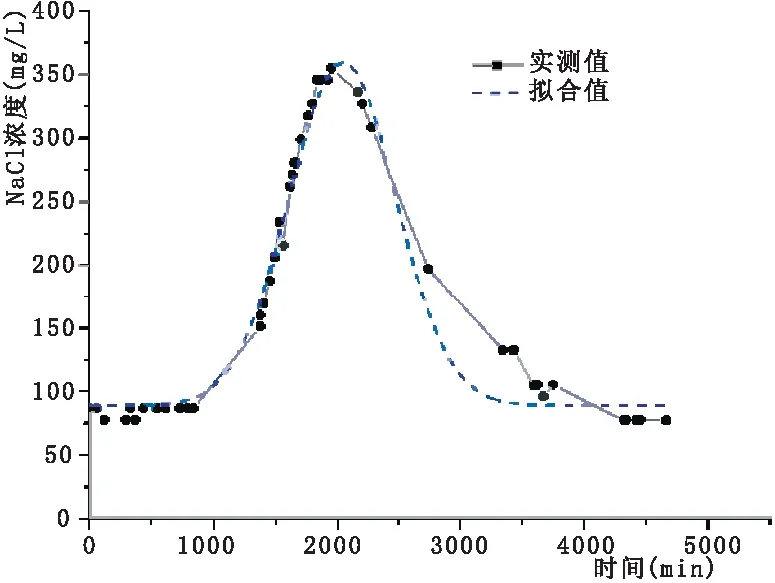
图4　测点二浓度拟合图

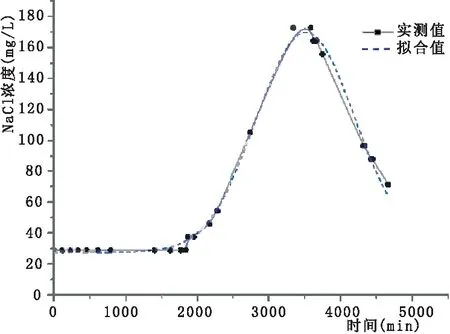
图5　测点三浓度拟合图

因此，得出弥散系数DL计算方法如下：

1)确定Cmax的值及其对应的数学期望，即x=μ=ut；

2)取0.607Cmax，从浓度曲线上找出拐点所在的位置，求出对应的x=ut+σ，由此得均方差σ值；

3)依照均方差公式得到DL=σ2/4t。

采用Origin软件中的Gaussamp公式对各测点试验数据进行非线性拟合，分别得到各测点的实际值与拟合值如图3～图5所示。

从而求得各点的纵向弥散系数DL如表2所示。

表2　弥散系数计算结果

理想的状态下，土柱中应该发生平衡吸附作用，但是当溶质与介质接触时间较吸附解吸作用时间更长的时候，一般用非平衡或速率受限制的反应过程来描述该作用。当溶质运移时，溶质会被吸附到介质中，出现滞留，当峰值浓度流过观测点后，吸附的溶质从介质中解吸出来，在之后一段时间保持比较高的浓度。本次试验中，证明了溶质接触时间较短情况下，这种“拖尾”现象在黏土中十分显著。

4　结语

根据试验结果得出以下结论：

(1)饱和黏性土体弥散系数随着渗流路径的增加而增大。

(2)溶质在接触时间较短情况下，饱和黏性土中离子的吸附解吸过程依然明显，从而造成穿越曲线的“拖尾”现象。

本次采用的一维模型试验，优点是能够方便快速的确定土体的参数，但实际污染环境十分复杂，土体的各向异性、污染物的性质、地下水渗流条件等均对污染物的运移有较大的影响，如何将试验结果合理的应用到实际工程中，有待进一步研究。

[1]中华人民共和国环境保护部.2014年中国环境公报.2015.5-19.

[2]中华人民共和国国土资源部.2013中国国土资源公报.2014.30.

[3]李霄，都基众，等.应用土柱试验求解地下含水介质弥散系数[J].地下水.2012.20-22.

[4]陈亮，梁越.两种典型溶质模拟污染物在沙性土壤中的运移试验研究[J].江苏农业科学.2007.304-308.

[5]谢焰，谢海建，等.填埋场底土污染物浓度实测值和理论解的比较[J].自然灾害学报.2009.62-69.

Experimental Study on One-dimensional Model of Contaminant Transport in Saturated Cohesive Soil

HU Qin-jun，YANG Hui-lin，ZHANGLei

(Tianjin institute of geotechnical investigation surveying,Tianjin300191,China)

Based on the one-dimensional model test,sodium chloride solution was used to simulate soluble contaminants,the contaminant migration in saturated cohesive soil was researched.The related changes of breakthrough curve as the increased infiltration path was analyzed,andthe method for determining the dispersion coefficient was proposed.The results showed that with the increase of infiltration path,the dispersion coefficient increased gradually.When the pollutants and saturated cohesive soil contact for short time,the adsorption-desorption phenomenon of ion was still obvious.The experimental results were available for reference for the establishment of the model for pollutants migration and the pollution forecast.

Soluble contaminant；saturated cohesive soil；dispersion coefficient and adsorption-desorption

2016-05-18

胡钦君(1979-)，男，山东巨野人，工程师，主要从事岩土工程勘察工作。

X53

A

1004-1184(2016)05-0077-03