ZPW-2000A型无绝缘移频轨道电路补偿方案研究

薛红岩

(中铁第一勘察设计院集团有限公司，西安　710043)



ZPW-2000A型无绝缘移频轨道电路补偿方案研究

薛红岩

(中铁第一勘察设计院集团有限公司，西安710043)

在现场的应用中，ZPW-2000A型无绝缘移频轨道电路在安全性和可靠性方面有着显著优势，但其分路特性的改善是需要关注的问题。采用电平衰耗法的计算方法，对无补偿电容、有补偿电容和有最佳补偿电容时的无绝缘轨道电路的分路特性进行分析，并用Matlab软件仿真得到轨面各点的分路灵敏度和分路残压比较结果。结果表明，补偿电容对轨道电路的分路特性有明显的改善作用，而找到最佳补偿电容值对轨道电路进行补偿，不但能同时保证轨道电路全程可靠分路，并且降低了分路残压，使得无绝缘轨道电路的分路特性更稳定。

无绝缘轨道电路；补偿电容；分路特性；分路灵敏度

1　概述

ZPW-2000A型无绝缘轨道电路具有较高安全性，自2003年至今，在全路得到了全面运用，技术成熟。由于装设无绝缘轨道电路不切割钢轨，面对越来越高的列车运行速度，无绝缘成为轨道电路必须具备的条件，这是各国纷纷采用无绝缘轨道电路的主要原因。无绝缘移频轨道电路虽然在目前应用广泛，但也并不是尽善尽美的，根据现场使用的情况，仍需对其做进一步的优化和改进，才能适应快速发展的高速铁路的要求。其中补偿电容的设置对无绝缘轨道电路的传输特性和分路特性的提高起到了非常大的作用，但现阶段的工程设计和实际应用中，对无绝缘轨道电路补偿电容的容值的大小都是固定在某几个值上[1]，这其实限制了补偿的作用，在某些特殊恶劣条件下，并没有达到最佳的补偿效果。本文通过对不加补偿电容、加装补偿电容的现有方式对ZPW-2000A型无绝缘轨道电路分路特性影响的分析，提出寻求轨道电路的最佳补偿方案的方法，并结合工程实际，验证其可行性。

2　无绝缘轨道电路分路状态现状的分析

2.1不加补偿电容时轨道电路分路灵敏度的计算

分路状态最不利条件下(道床电阻为无穷大时)，在没有加补偿电容时，ZPW-2000A型无绝缘轨道电路的等效电路如图1所示[2，3]。

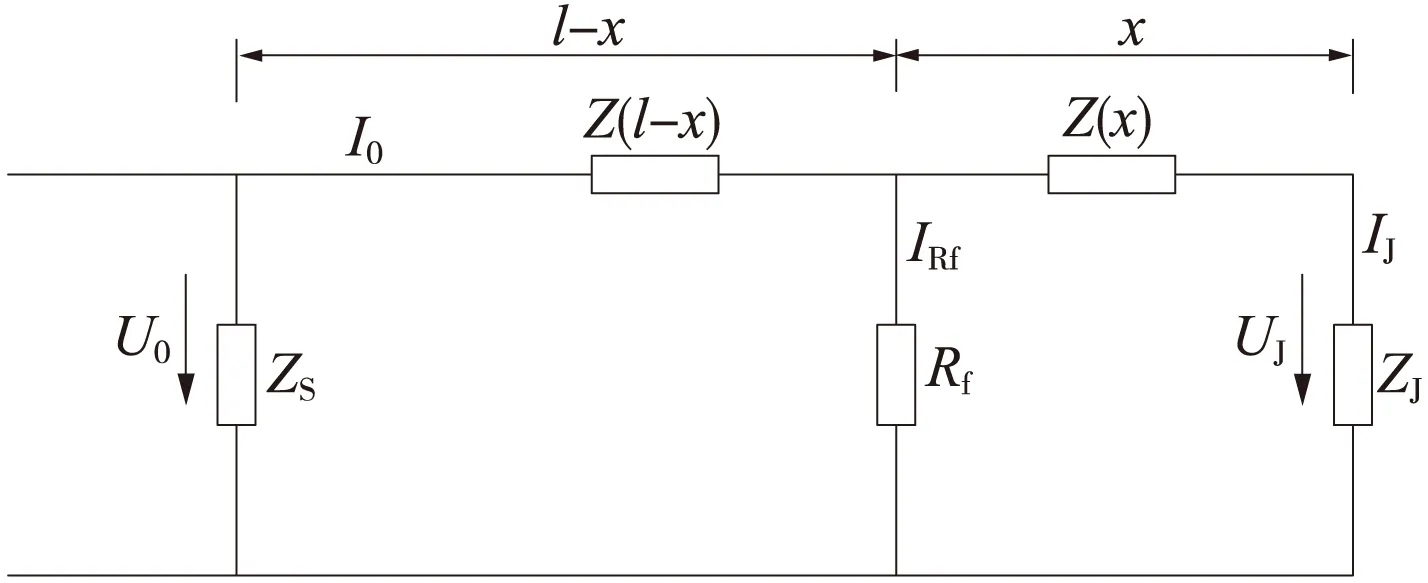
图1　无补偿电容时轨道电路的等效电路

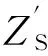
列车在轨面任意点分路时，轨道电路衰耗为

(1)

式中，P0为发送设备向电气绝缘节调谐单元的右侧轨道输入的功率；PJ为接收设备输出给电气绝缘节调谐单元和负载的功率。

根据图1所示的轨道电路等效电路图，用接收端的电压UJ、电流IJ表示发送端的输入电压U0、电流

(2)

(3)

当列车在轨道电路终端(接收端)分路时，x=0，这时的轨道电路衰耗为

(4)

将式(2)、式(3)代入式(4)中，可得

b0=4.343×

(5)

当列车在始端(发送端)分路时，x=l，这时的轨道电路衰耗为

(6))

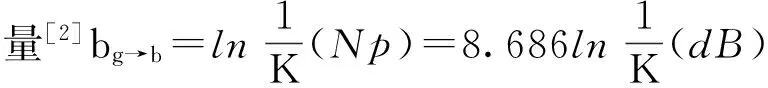
(7))

式中，K为接收器的返还系数。所以，列车在轨道电路终端和始端可靠分路必须满足衰耗条件式(8)或式

(8)

(9)

式中，bmax为轨道电路允许的最大衰耗量。由于极限分路灵敏度在轨道电路的两端[4]，所以无补偿轨道电路的极限分路灵敏度必然在始端或终端，将式(8)、式(9)两个不等式取等号，使其变为等式，再用数值迭代法即可求得发送端和接收端的的分路灵敏度。

由此推理出，在轨道电路任意点分路必须满足的条件是

(10)

假设在频率为1 700 Hz、轨道长度1.5 km时，轨面各点的分路灵敏度通过上述计算得到如图2所示的曲线。

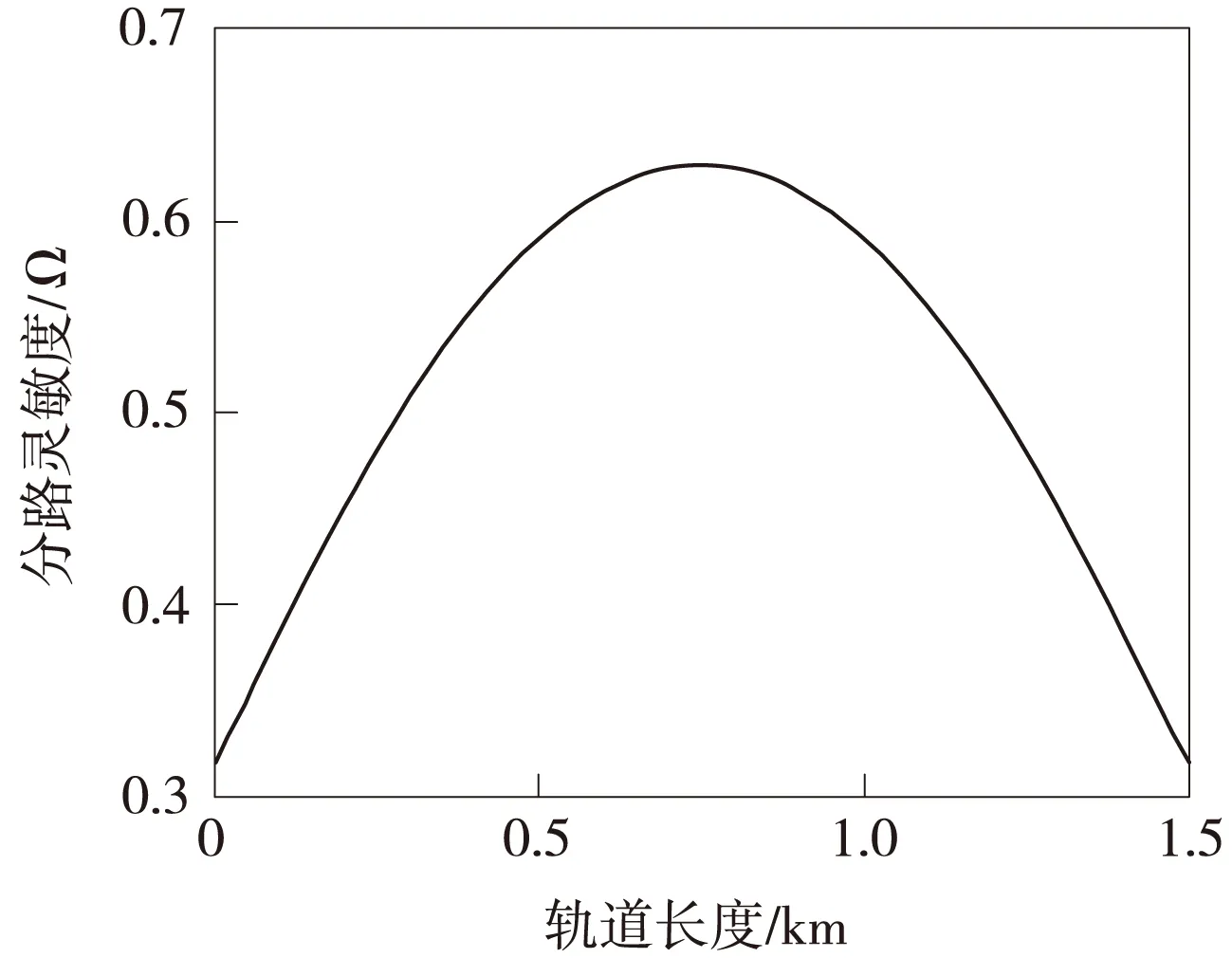
图2　无补偿电容时轨面各点的分路灵敏度

图2中坐标原点为轨道电路终端。从图2可以看出，无绝缘轨道电路在无补偿的情况下，最难分路的地方在两端，而有较好分路特性的地方在中间，也就是说，不设补偿电容的轨道电路的长度只能在中间分路性能较好的范围内取值，且轨面各点分路的难易程度相差较大，不利于调整。

2.2加装补偿电容时轨道电路分路灵敏度的计算

在有补偿电容的无绝缘轨道电路分路特性的分析中，很难定量计算出其轨面各点的分路灵敏度大小，而采用电平衰耗的方法对其分路状态分析较为简便[5，6]。

有补偿电容时，终端分路的轨道电路等效电路如图3所示。

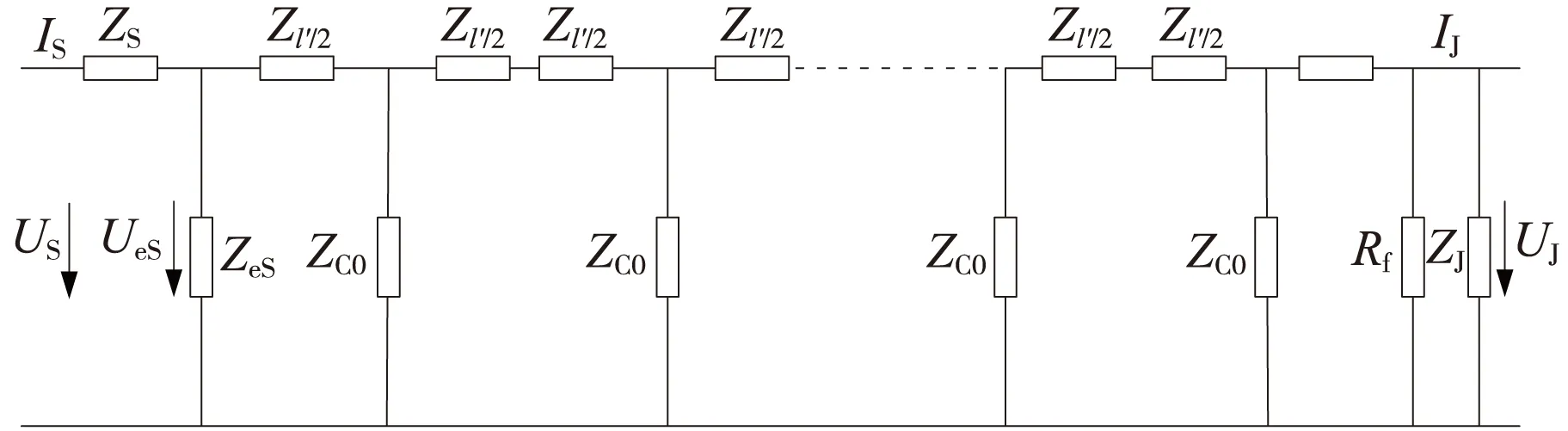
图3　终端分路时轨道电路等效电路

有补偿电容时，始端分路的轨道电路等效电路如图4所示。

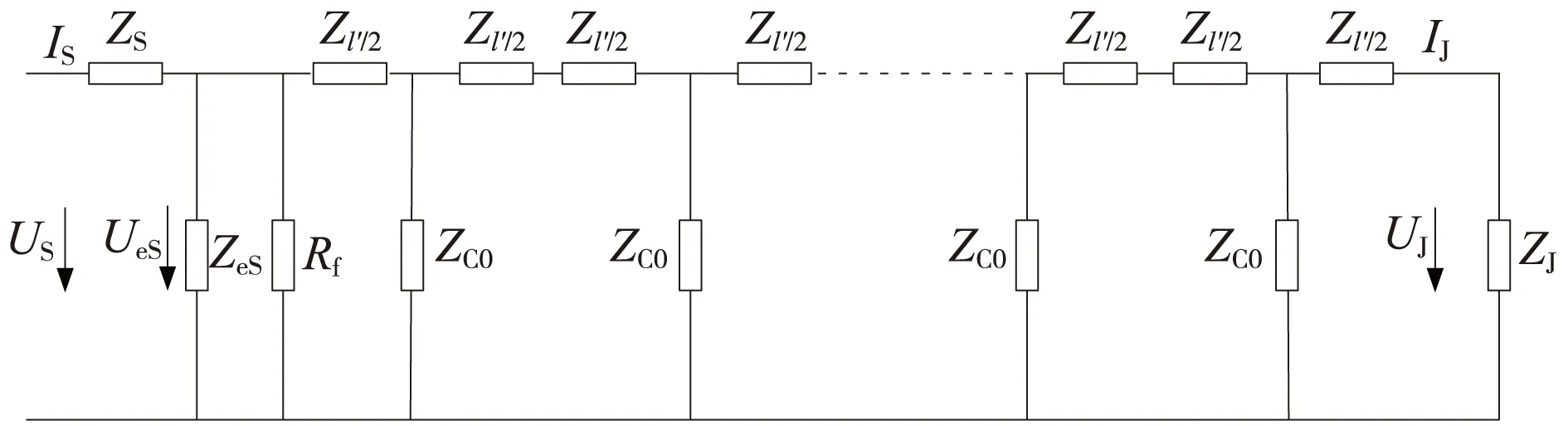
图4　始端分路时轨道电路等效电路

要得到其分路衰耗，先要计算一个补偿节的T型等效电路的衰耗。补偿节T型等效电路如图5所示。

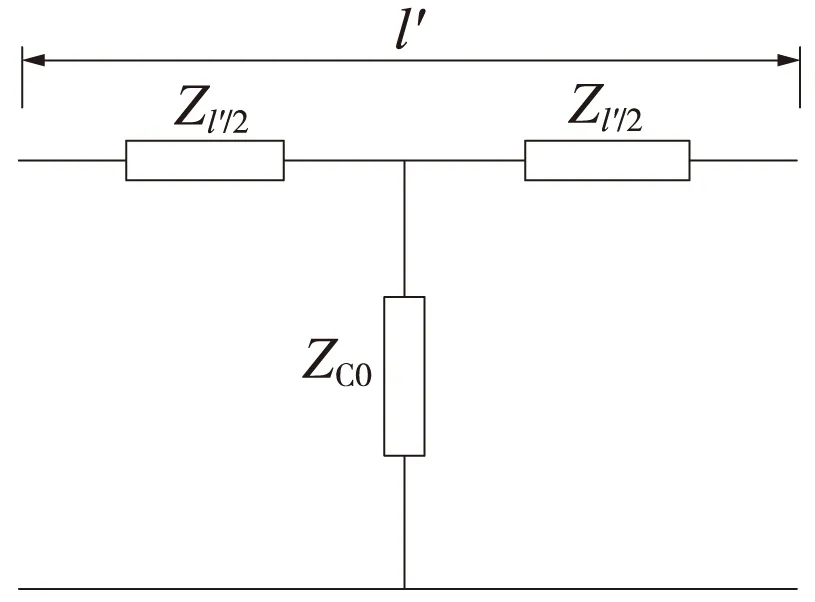
图5　T型等效电路

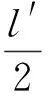
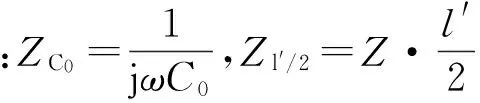
图5所示的T型等效电路的四端网系数为

(11)

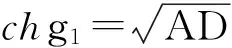
(12)

(13)

(14)

(15)

(16)

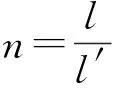
(17)

此四端网的特性阻抗记作ZT，ZT与四端网A参数之间的关系

(18)

列车在轨道电路上分路所引起的衰耗主要有两种[2]：一种是分路衰耗，另一种是失配衰耗。

终端分路衰耗

(19)

终端与钢轨的失配衰耗

(20)

始端分路衰耗

(21)

式中，UeS为ZeS的端电压。

始端与钢轨失配衰耗

(22)

要使接收端可靠分路，必须满足衰耗条件[2]

(23)

发送端可靠分路，必须满足的衰耗条件是[2]

(24)

同样将上述两式的大于等于号取等号，再用数值迭代法即可求得发送端和接收端的的分路灵敏度。

加了补偿电容后，极限分路灵敏度的位置很难确定，所以不便用分路灵敏度的方法来表征其整个轨道电路的分路特性，而采用ZPW-2000A的标准分路电阻(0.15 Ω)对轨道电路任意点分路时的分路残压来表征其分路性能。

在陇海线天兰段天水至南河川区间下行14019G区段，频率为1 700 Hz、轨道长度1.3 km， 同等条件下对无补偿情况和有补偿情况的全程分路残压比较如图6所示。

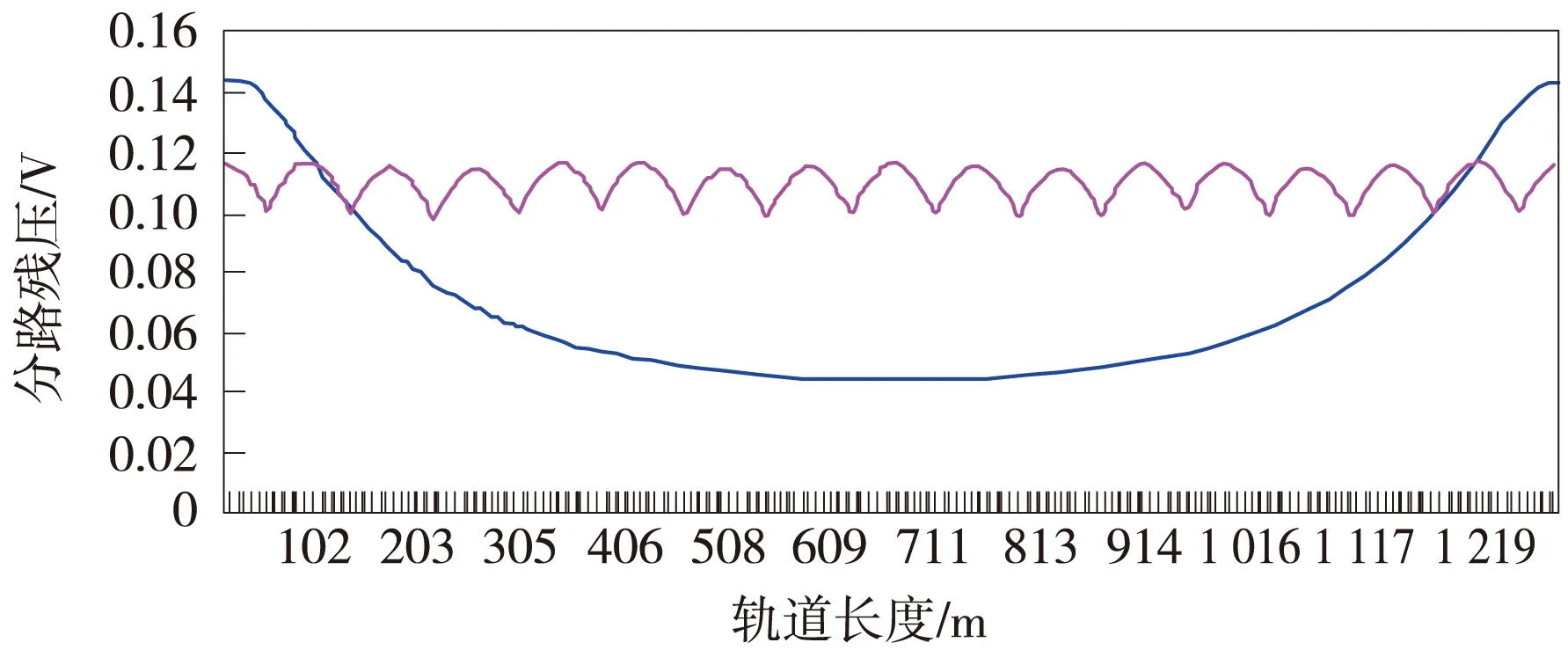
图6　陇海线天水之南河川区间14019G有补偿和无补偿轨道电路全程的分路残压比较

图6中坐标原点为轨道电路始端；横坐标为轨道长度(m)，纵坐标为分路残压(V)；向下凹的光滑曲线为无补偿的分路残压，波浪线为有补偿的分路残压。从分路残压的角度可以看出，补偿电容对轨道电路整体的分路灵敏度有很大的提高，但是补偿电容的加入打乱了原本轨道电路轨面各点分路灵敏度有规律的排列，使得轨面上各点的分路灵敏度情况复杂化。

3　最佳补偿方案的研究

为了稳定轨道电路在不同地点的分路灵敏度，寻求最佳的补偿效果，图7中绘出了频率为1 700、2 000、2 300、2 600 Hz时，轨道区段均匀补偿时的最佳补偿电容值与道床电阻的关系曲线。

从图7可以看出：在同频的轨道区段内最佳补偿电容值随着道床电阻的增大而减小；在不同频的轨道区段内最佳补偿电容值随着信号频率的增大而减小。当轨道区段的信号频率一定的时候，钢轨的阻抗值是一个固定值，集中补偿方式的最佳补偿电容值与道床电阻成反比；而当道床电阻值一定、不同轨道区段的信号频率变化的时候，钢轨的阻抗值会发生变化，钢轨阻抗值随着信号频率的增大而增大，所以补偿电容值随信号频率的增大而减小。

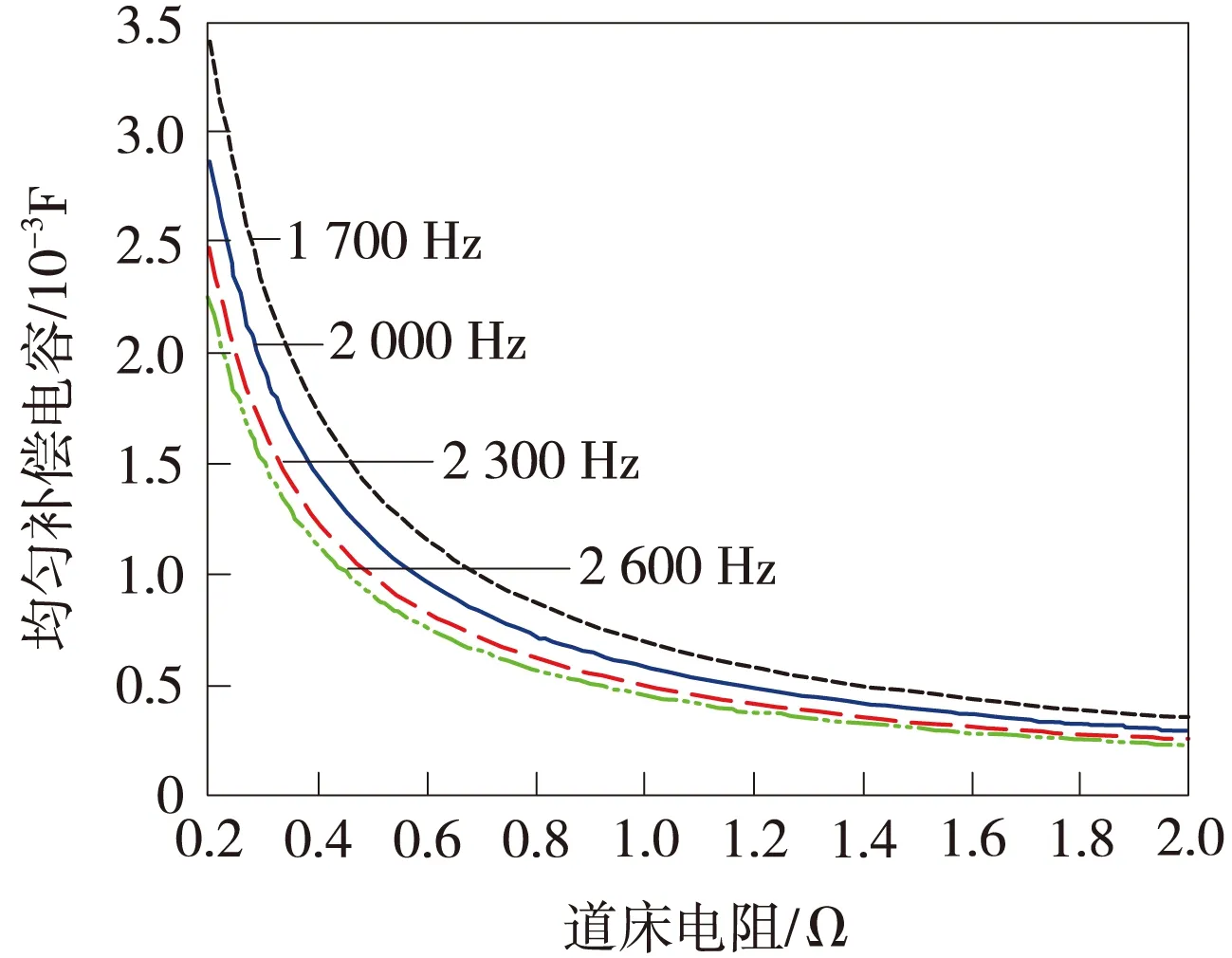
图7　频率不同的轨道电路中补偿电容与道床电阻的关系

4　最佳补偿电容值的确定

最佳补偿电容值也就是使整个区段内的补偿电容等效为一个连续的均匀分布的补偿电容时的电容值[7，8]。确定最佳补偿方式的补偿电容值，也就是要使整个轨道电路的特性阻抗趋近于纯阻性，并使传输衰耗最小[9]。最佳补偿电容值也就是使等效的连续电容补偿网络的衰耗常数达到最小时的集中补偿电容值，可以用数值迭代方法确定。

实际电容补偿就是按照等间距设置补偿电容[10，11]。电容集中补偿的轨道电路的等效T型四端网络如图8所示。

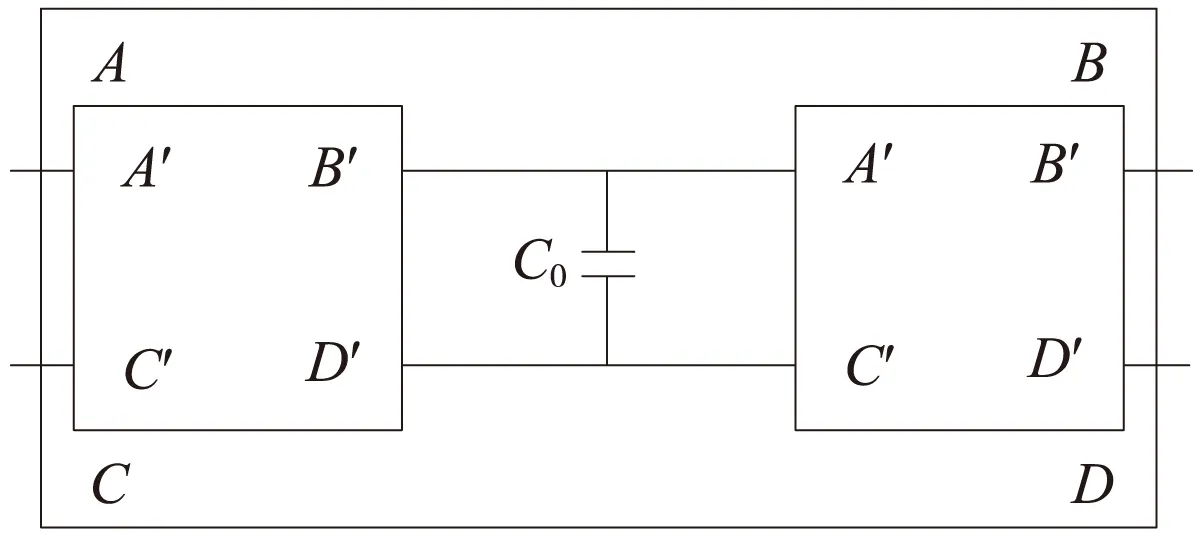
图8　T型等效四端网络

经过一系列矩阵变换，可以计算出包括补偿电容C0在内的三个级联的四端网合并而成的四端网络的系数A、B、C、D

(25)

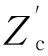
由此可以推出

(26)

理想的连续电容补偿的轨道电路含有一个补偿电容的T型等效网络的衰耗常数由式(26)确定[12-13]。可以看出轨道电路的衰耗常数β′随着g模值的增加而增加。所以，只要求出g的最小模值就求出了最小的衰耗常数[14-15]。

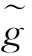
(27)

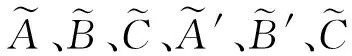
同样以上述陇海线天兰段天水至南河川区间下行14019G区段为例，频率为1 700 Hz、轨道长度1.3 km。经过迭代运算得到：在1 700 Hz区段的最佳集中补偿电容值为50.4 μF，即在轨道区段的每100 m处并联1个50.4 μF的补偿电容。同等条件下全程分路残压比较如图9所示。

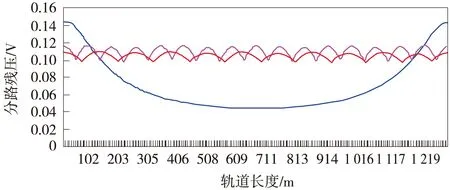
图9　陇海线天水至南河川区间14019G最佳补偿、实际补偿和无补偿轨道电路全程的分路残压比较

图9中比图6中多的较为光滑的波浪线为最佳补偿的分路残压。可以看出，最佳补偿电容比实际1 700 Hz区段中固定容值的补偿电容更能提高轨道电路的分路灵敏度，且轨面各点的分路灵敏度虽仍有起伏，但已改善了很多。

5　结语

不加补偿电容的无绝缘轨道电路，在分路的情况下，轨面各点的分路灵敏度分布曲线呈开口向下的抛物线，其极限分路灵敏度在轨道电路的始端或终端。而加了补偿电容的无绝缘轨道电路分路时，轨面各点的分路灵敏度情况变得没有规律，极限分路灵敏度的位置亦不确定。对于ZPW-2000A的无绝缘轨道电路来说，加了补偿电容使得在任意点分路时的分路残压分布在一个较小的范围内，降低了始、终端附近的分路残压，改善了分路状态。而更精确地找到轨道电路的最佳补偿电容值，不但能同时保证轨道电路全程可靠分路，并且降低了分路残压，较现有的集中补偿电容值所得到的轨道电路全程分路残压曲线更优、分路性能更好。

本文是从等间距(100 m)设置补偿电容的角度出发来研究其对ZPW-2000A型无绝缘轨道电路的分路特性的影响，下一步还应从调整补偿电容的间距(或为不等间距)的角度进行研究，以便找到稳定轨道电路分路灵敏度的方法。

[1]陶启沪.铁道信号基础设备及原理[M].北京:中国铁道出版社，1992.

[2]费锡康.无绝缘轨道电路原理及分析[M].北京:中国铁道出版社，1993.

[3]赵志，程荫杭.无绝缘轨道电路死区段的计算方法[J].铁道学报，2000，22(5):51-54.

[4]赵会兵，章宇舟，汪希时.电容补偿轨道电路若干问题的研究[J].铁道学报，1998，20(4):77-79.

[5]赵志.谐振式无缘轨道电路传输特性及仿真的研究[D].北京:北方交通大学，2000.

[6]赵志，程荫杭.无绝缘轨道电路死区段的计算方法[J].铁道学报，2000，22(5):51-54.

[7]张少平.UM71型无绝缘轨道电路的调试与开通[J].铁道通信信号，1994，30(7):15-17.

[8]李烨，徐中伟.电气化铁路移频自动闭塞信号传输仿真的研究及应用[J].铁道学报，2003，25(6):66-70.

[9]陈志颖.高速铁路隧道群地段信号维护技术及体制的完善和应用研究[J].铁道标准设计，2015，59(2):110-113.

[10]袁彦.轨道电路的建模与仿真[D].成都:电子科技大学，2005.

[11]马涛，米根锁，齐东.基于灰色理论ZPW-2000A无绝缘轨道电路故障风险分析[J].铁道标准设计，2013(4):115-118.

[12]董昱.区间信号与列车运行控制系统[M].北京:中国铁道出版社，2008.

[13]贾晨子.轨道电路参数测量和调整的研究[D].北京:北京交通大学，2007.

[14]阿·米·布列也夫，尤·阿·克拉夫，阿·付·希师良柯夫.轨道电路分析与综合[M].北京:中国铁道出版社，1981.

[15]鲁恩斌，李宏一.区间及站内轨道电路干扰问题的分析和处理[J].铁道通信信号，2009，45(3):35-36.

Research on Compensation Capacitance Scheme of ZPW-2000A Non-insulated Track Circuit

XUE Hong-yan

(China Railway First Survey and Design Institute Group Co.， Ltd.， Xi’an 710043， China)

The field application shows the obvious advantages of ZPW-2000A non-insulated track circuit in security and reliability， but its shunt characteristic still needs to be improved. The shunt characteristics of the track circuit with and without compensation capacitor and with optimal compensation capacitor are analyzed and shunt sensitivity and shunt residual voltage of the track circuit at each track surface point are compared and simulated with MATLAB simulation software. The results show that the compensation capacitor improves remarkably the shunt characteristic of the track circuit and the best compensation capacitance can not only guarantee track circuit reliability but also reduce the shunt residual pressure， and make the shunt characteristic of the non-insulated track circuit more stable．

Non-insulated track circuit， Compensation capacitor; Shunt characteristics; Shunt sensitivity

2016-01-20；

2016-02-19

薛红岩(1983—)，女，工程师，2009年毕业于兰州交通大学交通信息工程及自动化专业，工学硕士，E-mail：xue_hy@163.com。

1004-2954(2016)08-0139-05

U284.2

ADOI:10.13238/j.issn.1004-2954.2016.08.029