行波及相干效应对超千米跨度斜拉桥多维多点随机地震响应的影响
2016-10-21范晨阳郑史雄
范晨阳,郑史雄,陈 航,张 金
(西南交通大学土木工程学院,成都 610031)
行波及相干效应对超千米跨度斜拉桥多维多点随机地震响应的影响
范晨阳,郑史雄,陈航,张金
(西南交通大学土木工程学院,成都610031)
为了研究行波及相干效应对超千米跨度公铁两用斜拉桥地震响应的影响,基于通用有限元软件ANSYS,借助高效的虚拟激励法分别得到考虑两种效应的结构地震响应值,通过对比研究,结果表明:(1)仅考虑行波效应时,在视波速取500 m/s工况下,主梁纵向位移和竖向位移出现最大均方根值,行波效应对主梁纵向位移响应影响最为显著;(2)仅考虑相干效应时,主梁纵向位移和横向位移在部分相干工况下出现最大均方根值,主梁跨中横向位移的均方根值为0.274 m,较一致激励(完全相干)增大了126.4%;(3) 两种效应对结构1号边墩、2号辅助墩和3号主塔的不同地震响应的影响程度存在较大差异,需具体响应具体分析。通过各具体工况下的结果对比,得出超大跨度斜拉桥地震响应分析考虑行波和相干效应十分必要的结论。
斜拉桥;公铁两用桥;行波效应;相干效应;随机地震场模拟;地震反应分析
随着我国公、铁路网逐渐发展和完善,一大批跨江、跨海大桥被提上议程。大跨度桥梁作为主要交通路线的重要节点,一旦损坏,将造成不可预计的经济损失。所以针对交通生命线中重要的超大跨度桥梁进行专门的地震响应研究具有重要意义。鉴于此,很多学者对桥梁结构的地震响应进行了研究。中国2008年颁布的《公路桥梁抗震设计细则》引入了一种考虑概率性的随机振动分析法,它是建立在地面运动统计性基础上,是一种先进的分析手段和方法,因为其高效性在工程界已被广泛地运用。Lin[1]等将平稳随机地震激励应用到输油管线,将输油管线看作是多点支撑的连续梁来求解。Perott[2]、Harichandran[3]也对随机振动方法进行了深入的研究。林家浩、张亚辉、Q.S.Li、F.W.Williams等[4-7]将虚拟激励法应用到了高层结构以及大跨度桥梁结构受地震作用的三维随机响应;贾宏宇等[8]应用大型商用软件ANSYS中谐分析模块,采用大质量块法,直接采用绝对位移法求解,进一步提高了计算效率。
在桥梁结构抗震分析时,输入的地震动考虑空间效应更为合理,因此王蕾等[9]在考虑地形影响和多点激励的大跨度高墩桥地震响应分析中指出,在50 m范围内,地基各点振动的相位和幅值差别较大,所以行波效应对超大跨度桥梁的影响是很大的,考虑行波效应也是十分必要的。洪浩等[10-11]研究了在不同视波速下,山区高墩大跨刚构桥的地震响应规律及空间相干效应对山区高墩刚构桥不同墩高的地震响应规律。丁阳[12]等在部分相干效应对大跨度空间结构随机地震响应的影响一文中详细地研究了部分相干对大跨度斜拉桥的地震响应规律。
目前,国内外学者对行波效应和相干效应的研究多数集中于中小跨度桥梁,对特大跨度桥梁的研究较少[13]。但随着我国经济社会的发展和建造技术的进步,超千米跨度铁路桥梁不断涌现,考虑到铁路桥梁承受荷载大,且列车线路轨道等的平顺要求更高,因此,该类桥梁无论在设计还是施工方面都要比同等跨度公路桥梁要求更加严格。以世界上唯一一座超千米跨度公铁两用斜拉桥为研究对象,考虑行波效应和相干效应对其地震响应的影响,旨在为此类超大跨度斜拉桥抗震响应研究提供一定的参考。
1 理论分析
1.1多维多点平稳激励理论分析
对于有m个地面支撑、n个自由度的离散线性结构考虑3个平动方向的地震作用后,其多维多点的地震激励运动可以表示如下的矩阵形式[14,15]
(1)
式中,Xb为3×m维列向量,代表m个支撑的地面强迫位移;Xs为3×n维列向量,代表结构系统所有非支撑节点的位移;Pb为3×m维列向量,代表m支撑受到的3个地震方向的地震力;M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵;下标s表示非支撑节点,b表示支撑节点。
将式(1)按第二项展开可得到
(2)
(3)
(4)
(5)
只要支撑质量矩阵足够大,就能保证支撑处的地面加速度和支撑地震响应的加速度相等,从而大大简化式(1)求解(即大质量块法)。
将式(5)带入到式(1)第一项中展开后可以得到
(6)
设支撑处虚拟激励荷载为
(7)
其中P是由(3m×3m)功率谱矩阵S0(iω)=P*PT分解得到。将式(7)带入式(6)整理可得
(8)
考虑到等效荷载项中的虚拟力较小,将其忽略,得到虚拟激励动力方程
(9)
求解上式很容易得到绝对位移响应的功率谱矩阵
(10)
响应的功率谱求解是随机振动的核心问题,求得响应功率谱后可得各阶谱矩阵,以及响应均值和方差等概率特征。
1.2平稳随机地震场模拟及参数选取
地面加速度功率谱采用杜修力—陈厚群模型[16]
(11)
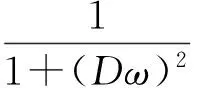
采用屈铁军-王君杰等部分相干模型,即
(12)
式中,a(ω)=a1ω2+a2;b(ω)=b1ω2+b2;a1=0.000 016 78;a2=0.001 219;b1=-0.005 5;b2=0.767 4。
2 工程简介及模型建立
以某超千米跨度斜拉桥为算例,桥梁全长2 300 m,主跨1 092 m,桥梁总体跨径布置为(142+462+1 092+462+142) m,主梁采用钢桁架结构,桥面宽度35 m,主梁高度16 m,桥塔与桥墩均采用混凝土结构,两主塔高度325 m,每一个索面由36对索组成。采用大型商用软件ANSYS建立桥梁有限元模型,主梁弦杆和辅助墩均采用单元Beam4模拟,桥塔与钢轨均采用单元Beam44模拟,斜拉索采用link8单元模拟,主梁和主塔横梁、辅助墩采用节点耦合来模拟支座,文中主要研究桥梁结构的整体地震响应,故底座板、轨道板和铺装层均以mass21单元模拟,忽略其刚度影响。桥梁整体布置、三维有限元计算模型如图1和图2所示,其中x为顺桥向,y为竖桥向,z为横桥向。
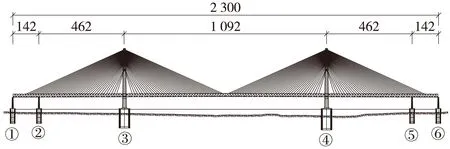
图1 桥梁整体布置(单位:m)

图2 三维有限元计算模型
3 桥梁地震响应分析
斜拉桥主梁为桁架结构,在研究主梁沿跨度方向的响应均方根值时,取中桁下弦杆为讨论对象。在进行多维多点地震响应分析时,采取惯用的大质量块法加载,大质量一般取结构自重的105~108倍。出于结构设计通常采用包络值的原则,本文将重点关注结构地震最大响应,超大跨度斜拉桥主梁受力较小,主要关心主梁位移响应;边墩、辅助墩和主塔均重点关注底部约束位置处的内力响应。
3.1行波效应对桥梁地震响应的影响
当桥梁各下部支撑空间距离较大时,由于实际地震波具有一定的传播速度,使得同一地震波到达桥梁各下部支撑时存在相位差,需要考虑行波效应。本文考察了6种不同视波速工况,见表1。工况#A,视波速取无穷大,这相当于各支撑基础之间地震波的传递没有时间滞后,拥有相同的相位振动,即一致激励。

表1 考虑行波效应的计算工况
在不同视波速下主梁的位移响应均方根值沿跨度的分布曲线见图3。由图3看出,虽然在不同工况下具体响应值有所不同,但沿跨度方向的分布曲线变化趋势基本相似。需要注意的是3个方向的位移响应均方根值并非均在工况#A下出现最大值,纵向位移和竖向位移均在工况#D下出现最大值,产生这种情况原因在于行波效应对结构响应的影响程度与结构自身特性和视波速有关。
从图3(a)可以看出,各工况下主梁沿跨度方向的纵向位移曲线近似是一条直线,这是由于此类半漂浮结构的主梁在纵向是整体运动的,但是考虑到各杆件的伸缩变形和主梁横向变形的影响,主梁跨中纵向位移会略小于端部位移,位移曲线呈现“两头大中间小”的特点,工况#D下主梁纵向位移的均方根值为0.084 m,比一致激励的均方根值增大277.2%。图3(b)、图3(c)可以看出,主梁沿跨度方向的竖向和横向位移曲线分布不是完全对称的,这是由于考虑了行波效应的地震动作用是不对称的,进而结构响应也是不对称的;且沿跨度方向的响应曲线变化规律性不强,呈现波动性变化;还不难看出各工况下主梁与边墩、辅助墩和桥塔连接处有竖向位移,原因在于地震动输入采用了惯用的大质量块法,大质量块没有施加约束,导致大质量块产生了振动位移。工况#D下主梁跨中竖向位移的均方根值为0.299 m,比一致激励的均方根值增大11.2%。工况#A下主梁跨中横向位移的均方根值为0.425 m。
将不同视波速工况下1号边墩底、2号辅助墩底和3号桥塔底的纵向剪力和纵向弯矩的响应均方根值汇总见表2。
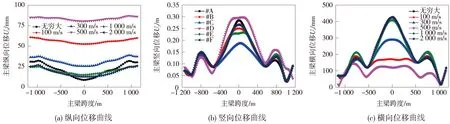
图3 主梁位移响应均方根值

截面位置1号边墩底2号辅助墩底3号主塔底内力#A#B#C#D#E#F纵向剪力/kN103010731067111010191087纵向弯矩/(kN·m)2.93E+043.38E+042.80E+043.52E+042.93E+043.27E+04纵向剪力/kN171617891779190316991812纵向弯矩/(kN·m)441350754224522344364949纵向剪力/kN3.09E+043.22E+043.20E+043.45E+043.06E+043.26E+04纵向弯矩/(kN·m)1.76E+062.03E+061.68E+062.17E+061.76E+061.96E+06
由表2可以看出,无论是一致激励还是考虑了行波效应,3号主塔的纵向剪力和纵向弯矩都比1号边墩、2号辅助墩大;1号边墩、2号辅助墩和3号桥塔的纵向剪力和纵向弯矩均在工况#D下出现最大值,分别为1 149 kN、36 200 kN·m,1 915 kN、5 425 kN·m和34 500 kN、2 170 000 kN·m,较一致激励分别增大了7.83%、19.89%、10.92%、18.35%、11.62%、23.60%。说明行波效应对1号边墩、2号辅助墩和3号主塔的纵向剪力的影响依次增加;对3号主塔的纵向弯矩影响较大,对1号边墩影响相对一般,对2号辅助墩影响相对较小。
3.2相干效应对桥梁地震响应的影响
通常来说,地震动中包含多种频谱成分的波,不同频谱的波在土层传播过程中出现不同程度的散射,其传递到各支撑基础时并不是完全相干,需考虑相干效应更符合实际。工况#G为完全相干(即抗震分析中所采用的一致激励法),工况#H为部分相干,工况#I为完全不相干。图4给出了在完全相干、部分相干和完全不相干3种工况下主梁的位移响应均方根值沿跨度方向的分布曲线图,在3种工况下变化趋势基本相似,但具体响应值却有所不同。
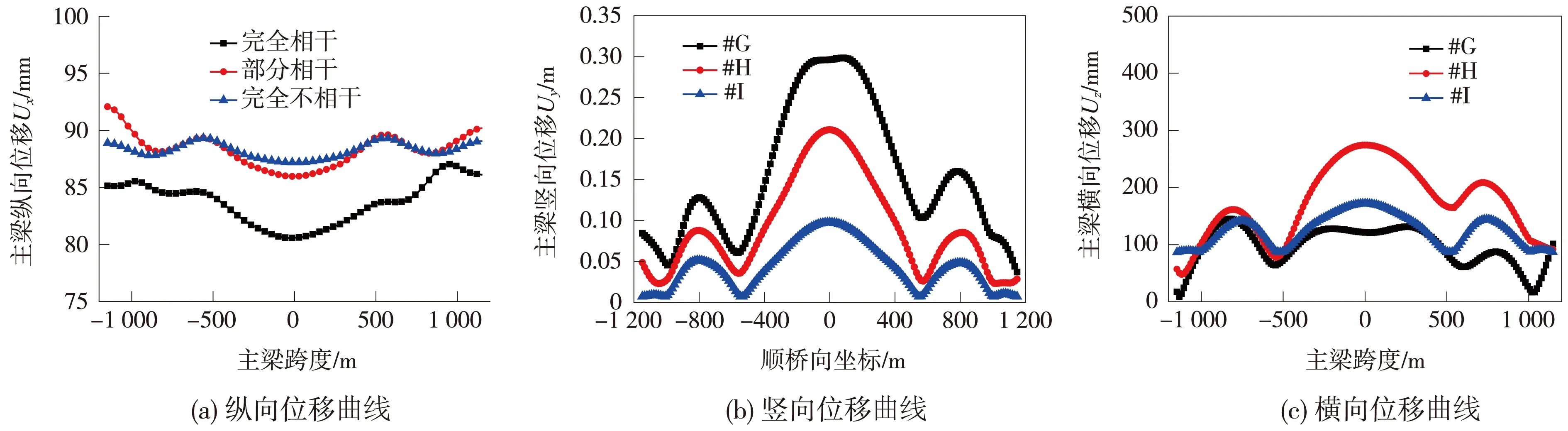
图4 主梁响应均方根值
图4(a)中,虽然各工况下主梁沿跨度方向的纵向位移曲线有所波动(同样呈现两头大中间小的特点),但每条纵向位移分布曲线的极大值和极小值差别最大不超过6 mm,说明主梁各点纵向位移近似相等。工况#H下主梁纵向位移的均方根值为0.092 m,比一致激励增大了4.8%。图4(b)中,在工况#G下主梁跨中竖向位移的均方根值为0.296 m。图4(c)中,在工况#H下主梁跨中横向位移的均方根值为0.274 m,较一致激励增大了126.4%。综上看出,主梁的位移响应并不是均在工况#G下出现最大值,产生这种情况可能由于相干效应和结构类型的不同,导致输入的谱矩阵的不同,谱矩阵所能激起的结构振型数目不同造成的。
不同相干工况下1号边墩底、2号辅助墩底和3号桥塔底的纵向剪力和纵向弯矩的响应具体值汇总见表3。
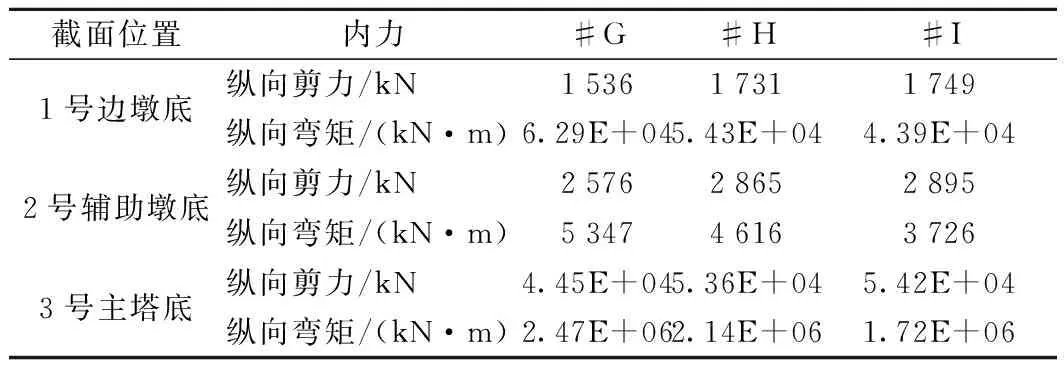
表3 控制截面内力比较
表3可以看出,是否考虑相干效应,3号桥塔的纵向剪力和纵向弯矩都比1、2号墩大;1号边墩、2号辅助墩和3号桥塔的纵向剪力均在工况#I下出现最大值,分别为1 749、2 895 kN和54 200 kN,较一致激励分别增大了13.91%、12.38%、21.84%; 1号边墩、2号辅助墩和3号桥塔的纵向弯矩均在工况#G下出现最大值,分别为62 900、44 500、2 470 000 kN·m,上述说明,相对1号边墩底、2号辅助墩底和3号主塔底的纵向弯矩,相干效应对其纵向剪力影响更加明显。
4 结论
本文借助虚拟激励法,研究了行波和相干效应对超千米跨度公铁两用斜拉桥地震响应的影响,得到如下结论。
(1)考虑行波效应下,并非各关键点结构响应均在一致激励作用下的地震响应产生最大均方根值,主梁的纵向位移和竖向位移在工况#D下出现最大值,较一致激励最大增大277.2%。
(2)相干效应对主梁的横向位移和纵向位移影响较明显,均在工况#H下出现最大值,分别较一致激励增大126.4%、4.8%。
(3)两种效应对结构1号边墩、2号辅助墩和3号主塔的不同地震响应的影响程度存在较大差异,需具体响应具体分析。
(4)对于超大跨度公铁两用斜拉桥,其承受的恒、活载都远大于同类跨度的公路桥梁。就地震响应分析而言,行波和相干效应对其影响更为显著,仅按传统的一致激励方法进行结构地震响应分析,会明显低估结构的地震响应。最后,针对同一位置、同一响应,应取不同工况组合的最不利响应作为结构抗震设计的依据。
[1]Lin Y K, Zhang R, Yong Y. Multiply Supported Pipeline under Seismic Wave Excitations[J]. Engineering Mechanics, 1990(16):1094-1108.
[2]Perotti F. Structural Response to Non-Stationary Multi-Support Random Excitation. Earthquake Engineering and Structural Dynamics, 1990(19):513-527.
[3]Harichandran R S. An Efficient Adaptive Algorithm for Large Scale Random Vibration Analysis[J]. Earthquake Engineering and Structural Dynamics, 1993(22):151-165.
[4]Li Q S, Zhang Y H, Lin J H. Seismic random vibration analysis of tall buildings[J]. Engineering Structures, 2004(26):1767-1778.
[5]Lin J H, Zhang Y H, Li Q S. Seismic spatial effects for long-span bridges,using the pseudo excitation method[J]. Engineering Structures, 2004(26):1207-1216.
[6]Lin J H,Lin S P,Zhong W X. Strategies for Developing Dynamic Program DASOS-J(D)of Offshore Structures[C]∥Proc. First World Conference on Computational Mechanics. Austin,Texas,USA,1986.
[7]Lin J H,Lu X,Zhong W X. Dynamic Response of jacket Platform to Random waves[C]∥Computer Modeling in Ocean Engineering, 1988:539-545.
[8]贾宏宇,郑史雄,陈冠桦.多维多点虚拟激励法在ANSYS中的应用[J].地震工程与工程振动,2012,32(4):7-12.
[9]王蕾,赵成刚,王智峰.考虑地形影响和多点激励的大跨高墩桥地震响应分析[J].土木工程学报,2006(1):50-53,59.
[10]洪浩,郑史雄,贾宏宇,等.考虑行波效应的高墩大跨刚构桥随机地震动响应研究[J].世界地震工程,2013(2):132-137.
[11]洪浩,郑史雄,贾宏宇,等.空间相干效应对山区高墩刚构桥随机地震动响应的影响[J].世界地震工程,2013(3):54-60.
[12]丁阳,张笈玮,李忠献.部分相干效应对大跨度空间结构随机地震响应的影响[J].工程力学,2009(3):86-92.
[13]郑史雄,张金,贾宏宇,等.大跨度斜拉桥多维多点随机地震激励响应分析[J].西南交通大学学报,2014,49(5):747-753.
[14]王新敏.ANSYS工程数值分析[M].北京:人民交通出版社,2008.
[15]Du Xiuli a,C. Houqun, Random simulation and its parameter determination method of earthquake ground motion[J]. Earthquake Engineering and Engineering Vibration, 1994,4(14):1-5.
[16]屈铁军,王君杰,王前信.空间变化的地震动功率谱的实用模型[J].地震学报,1996(1):55-62.
The Influence of Traveling Wave and Coherent Effects on Multi-dimensional and Multi-point Random Seismic Response of Super Long Span Cable Stayed Bridge
FAN Chen-yang, ZHENG Shi-xiong, CHEN Hang, ZHANG Jin
(School of Civil Engineering, Southwest Jiao Tong University, Chengdu 610031, China)
In order to study the influence of traveling wave and coherent effects on seismic response of the super long span railway double purpose cable stayed bridge, the seismic response of the structures with two effects are obtained with the aid of the efficient virtual excitation method based on the general finite element software ANSYS. The results of the comparative study show that:(1) when only the traveling wave effect is considered, the effect of the traveling wave on the longitudinal displacement of the main beam is the most significant, while the apparent wave velocity of 500 m/s is taken with the maximum root mean square value of both the longitudinal displacement and the vertical displacement of the main beam; (2)when only the coherence effect is considered, the longitudinal displacement and transverse displacement of the main beam appear under partially coherent conditions, the root mean square value of the transverse displacement of the main beam is 0.274 m, and the uniform excitation (totally coherent) increases by 126.4%; (3) the seismic responses of the two effects differ much in the structures of No.1 side pier, No.2 auxiliary Pier and No.3 main tower, and need to be analyzed specifically. By comparing the results of the specific conditions, we obtain that it is necessary to include traveling waves and coherent effect in the analysis of seismic response of large span cable-stayed bridges.
Cable-stayed bridge; Combined highway and railway bridge; Traveling wave effect; Coherence effect; Random seismic simulation; Seismic response analysis
2015-12-23;
2016-02-01
国家自然科学基金项目(51308465);中央高校基本科研业务费专项基金(2682014CX004EM)
范晨阳(1992—),男,硕士研究生,主要从事桥梁抗震研究,E-mail:FCYfanchenyang_@163.com。
1004-2954(2016)08-0054-05
U442.5+5
ADOI:10.13238/j.issn.1004-2954.2016.08.012
